26.4.1锐角三角函数应用(3)-冀教版九年级数学上册导学案(含答案)
文档属性
| 名称 | 26.4.1锐角三角函数应用(3)-冀教版九年级数学上册导学案(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 179.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-04 16:32:36 | ||
图片预览


文档简介
九年级数学教案(编号29)
课题: 26.4.1锐角三角函数应用3 备课人: 编制日期:10月26日
使用日期: 学科组长签字: 分管领导签字:
学习目标:1.理解方位角意义;
2.会用锐角三角函数解决关于方位角的实际问题。
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.AC和BD正好是东南西北线夹角的平分线
A在O的____________, B在O的____________,
C在O的____________, D在O的____________。
2.O在A的____________, O在B的____________,
0在C的____________, O在D的____________。
3.动手画一画某人在A处观望B在北偏东70°的方向上,则在B处观望A在B处的什么位置?
二、新知探究:【师生活动】学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
1、一艘船正以每小时30海里的速度由西向东追赶鱼群,在A处见小岛C在船的北偏东60°的方向上,已知小岛C为中心10海里的范围内有暗礁,船从A向东40分钟到B处看见小岛C在北偏东30°的方向,这艘船继续向东追赶鱼群有没有触礁的危险?
三、典例分析:【师生活动】 学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
1.某船以每小时36海里的速度向正东航行,在A点测得某岛C在北偏东60°的方向上,船行半小时后到B测得该岛在北偏东30°的方向上,已知该岛16海里内有暗礁
(1)试说明B点是否在暗礁区域外?
(2)若船继续向东航行,有无触礁危险?
四、题组训练: 【师生活动】 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
【A组】1、一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A地测得某灯塔位于它的北偏东30°的B处(如图1).上午9时行至C处,测得该灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里(结果保留根号).
2、如图2所示,机器人从A点出发,沿着西南方向,行了个单位到达B点后,观察到原点O在它的南偏东60°的方向上,则A点的坐标为 (结果保留根号).
3、(图6-31)上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
【B组】
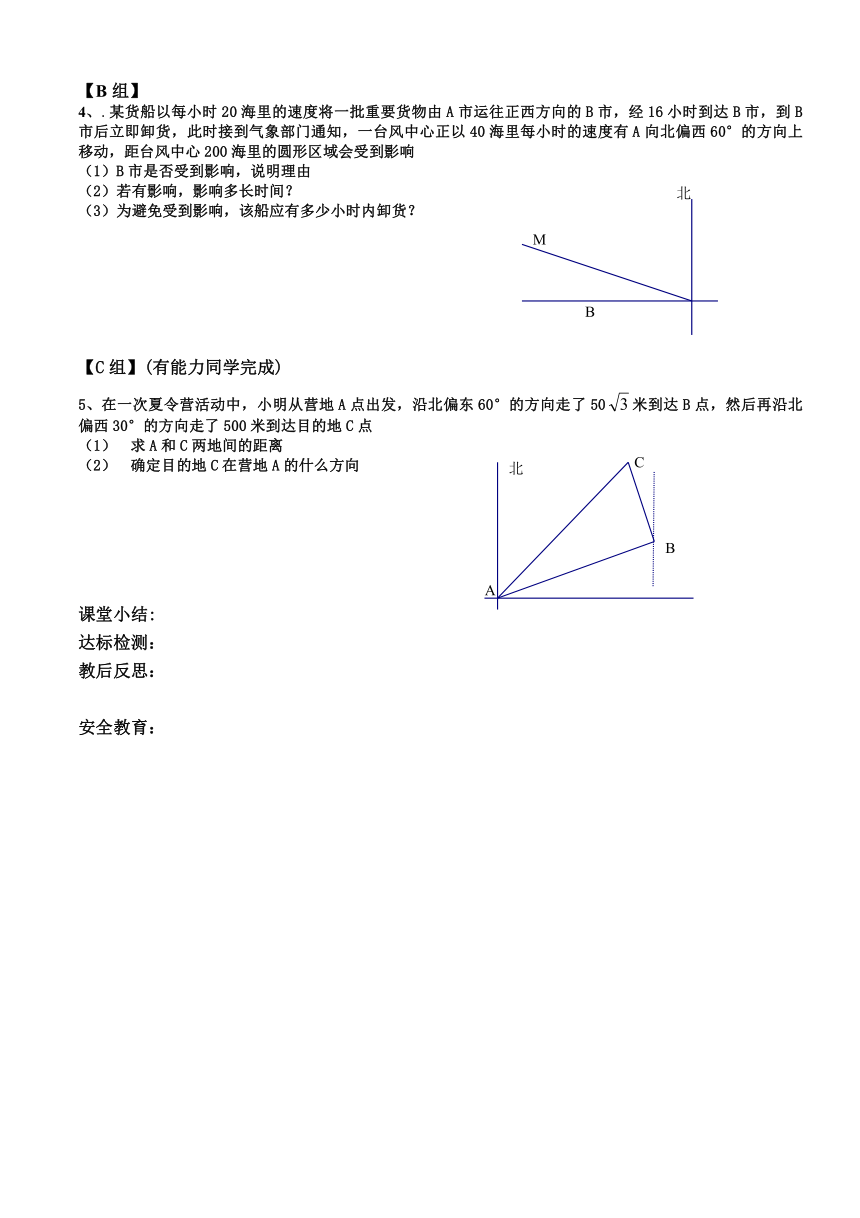
4、.某货船以每小时20海里的速度将一批重要货物由A市运往正西方向的B市,经16小时到达B市,到B市后立即卸货,此时接到气象部门通知,一台风中心正以40海里每小时的速度有A向北偏西60°的方向上移动,距台风中心200海里的圆形区域会受到影响
(1)B市是否受到影响,说明理由
(2)若有影响,影响多长时间?
(3)为避免受到影响,该船应有多少小时内卸货?
【C组】(有能力同学完成)
5、在一次夏令营活动中,小明从营地A点出发,沿北偏东60°的方向走了50米到达B点,然后再沿北偏西30°的方向走了500米到达目的地C点
求A和C两地间的距离
确定目的地C在营地A的什么方向
课堂小结:
达标检测:
教后反思:
安全教育:
九年级数学教案(编号29)
课题:26.4.2锐角三角函数应用3 姓名:
学习目标:1.理解方位角意义;
2.会用锐角三角函数解决关于方位角的实际问题。
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.AC和BD正好是东南西北线夹角的平分线
A在O的____________, B在O的____________,
C在O的____________, D在O的____________。
2.O在A的____________, O在B的____________,
0在C的____________, O在D的____________。
3.动手画一画某人在A处观望B在北偏东70°的方向上,则在B处观望A在B处的什么位置?
二、新知探究:【师生活动】学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
1、一艘船正以每小时30海里的速度由西向东追赶鱼群,在A处见小岛C在船的北偏东60°的方向上,已知小岛C为中心10海里的范围内有暗礁,船从A向东40分钟到B处看见小岛C在北偏东30°的方向,这艘船继续向东追赶鱼群有没有触礁的危险?
三、典例分析:【师生活动】 学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
1.某船以每小时36海里的速度向正东航行,在A点测得某岛C在北偏东60°的方向上,船行半小时后到B测得该岛在北偏东30°的方向上,已知该岛16海里内有暗礁
(1)试说明B点是否在暗礁区域外?
(2)若船继续向东航行,有无触礁危险?
四、题组训练: 【师生活动】 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
【A组】1、一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A地测得某灯塔位于它的北偏东30°的B处(如图1).上午9时行至C处,测得该灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里(结果保留根号).
2、如图2所示,机器人从A点出发,沿着西南方向,行了个单位到达B点后,观察到原点O在它的南偏东60°的方向上,则A点的坐标为 (结果保留根号).
3、(图6-31)上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
【B组】
4、.某货船以每小时20海里的速度将一批重要货物由A市运往正西方向的B市,经16小时到达B市,到B市后立即卸货,此时接到气象部门通知,一台风中心正以40海里每小时的速度有A向北偏西60°的方向上移动,距台风中心200海里的圆形区域会受到影响
(1)B市是否受到影响,说明理由
(2)若有影响,影响多长时间?
(3)为避免受到影响,该船应有多少小时内卸货?
【C组】(有能力同学完成)
5、在一次夏令营活动中,小明从营地A点出发,沿北偏东60°的方向走了50米到达B点,然后再沿北偏西30°的方向走了500米到达目的地C点
求A和C两地间的距离
确定目的地C在营地A的什么方向
答案:
知识链接:
北偏西45 南偏东45 北偏东45 南偏西45
南偏东45 北偏西45 南偏西45 北偏东45
南偏西70
新知探究
作CD⊥AB于D,
根据题意,AB=30×23=20(海里),∠CAD=30?,∠CBD=60?,
在Rt△ACD中,AD=CDtan30?=CD,
在Rt△BCD中,BD=CDtan60?=CD,
∵AB=AD?BD,
∴CD?CD=20(海里),
解得:CD=10>10,
所以不可能。
三、典例分析
(1)作CD⊥AB于D点,
设BC为x,
在Rt△BCD中∠CBD=60?,
∴BD=1/2x.
CD=x.
在Rt△ACD中∠CAD=30?tan∠CAD=CD/AD=,
∴
∴x=18.
∴点B是在暗礁区域外;
(2)∵CD==9,
∵9<16,
∴若继续向东航行船有触礁的危险。
四、题组训练
A组:1、 2、(0,) 3、11:44
B组:(1)如图,过点B作BD⊥AC交AC于点D,
∵在Rt△ABD中,∠BAC=90??60?=30?
∴BD=12AB
∵AB=20×16=320海里
∴BD=12×320=160海里。
∵160<200,
∴会受台风影响。
(2)在Rt△ADB中,AB=320海里,BD=160海里,则AD=160海里,
如图,BE=200海里,在Rt△BDE中,DE=120海里,
台风速度为40海里/小时,
故受影响的时间为:120×240=6(小时);
(3)要使卸货不受台风影响,则必须在点B距台风中心第一次为200海里前卸完货,
如图,BE=200海里,DE=120海里,
则AE=(160?120)海里,台风速度为40海里/小时,
则时间t=(160?120)/40=(4?3)≈4(小时),
答:为避免受到台风影响,该船应约在4小时内卸完货。
C组:(1)过B点作BE∥AD,
如图,∴∠DAB=∠ABE=60?.
∵30?+∠CBA+∠ABE=180?,∴∠CBA=90?.
即△ABC为直角三角形。
由已知可得:BC=500?m,AB=500?m,
由勾股定理可得:AC2=BC2+AB2,
所以AC=1?000(m);
(2)在Rt△ABC中,∵BC=500?m,AC=1?000?m,
∴∠CAB=30?,∵∠DAB=60?,∴∠DAC=30?.
即点C在点A的北偏东30?的方向。
课题: 26.4.1锐角三角函数应用3 备课人: 编制日期:10月26日
使用日期: 学科组长签字: 分管领导签字:
学习目标:1.理解方位角意义;
2.会用锐角三角函数解决关于方位角的实际问题。
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.AC和BD正好是东南西北线夹角的平分线
A在O的____________, B在O的____________,
C在O的____________, D在O的____________。
2.O在A的____________, O在B的____________,
0在C的____________, O在D的____________。
3.动手画一画某人在A处观望B在北偏东70°的方向上,则在B处观望A在B处的什么位置?
二、新知探究:【师生活动】学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
1、一艘船正以每小时30海里的速度由西向东追赶鱼群,在A处见小岛C在船的北偏东60°的方向上,已知小岛C为中心10海里的范围内有暗礁,船从A向东40分钟到B处看见小岛C在北偏东30°的方向,这艘船继续向东追赶鱼群有没有触礁的危险?
三、典例分析:【师生活动】 学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
1.某船以每小时36海里的速度向正东航行,在A点测得某岛C在北偏东60°的方向上,船行半小时后到B测得该岛在北偏东30°的方向上,已知该岛16海里内有暗礁
(1)试说明B点是否在暗礁区域外?
(2)若船继续向东航行,有无触礁危险?
四、题组训练: 【师生活动】 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
【A组】1、一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A地测得某灯塔位于它的北偏东30°的B处(如图1).上午9时行至C处,测得该灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里(结果保留根号).
2、如图2所示,机器人从A点出发,沿着西南方向,行了个单位到达B点后,观察到原点O在它的南偏东60°的方向上,则A点的坐标为 (结果保留根号).
3、(图6-31)上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
【B组】
4、.某货船以每小时20海里的速度将一批重要货物由A市运往正西方向的B市,经16小时到达B市,到B市后立即卸货,此时接到气象部门通知,一台风中心正以40海里每小时的速度有A向北偏西60°的方向上移动,距台风中心200海里的圆形区域会受到影响
(1)B市是否受到影响,说明理由
(2)若有影响,影响多长时间?
(3)为避免受到影响,该船应有多少小时内卸货?
【C组】(有能力同学完成)
5、在一次夏令营活动中,小明从营地A点出发,沿北偏东60°的方向走了50米到达B点,然后再沿北偏西30°的方向走了500米到达目的地C点
求A和C两地间的距离
确定目的地C在营地A的什么方向
课堂小结:
达标检测:
教后反思:
安全教育:
九年级数学教案(编号29)
课题:26.4.2锐角三角函数应用3 姓名:
学习目标:1.理解方位角意义;
2.会用锐角三角函数解决关于方位角的实际问题。
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.AC和BD正好是东南西北线夹角的平分线
A在O的____________, B在O的____________,
C在O的____________, D在O的____________。
2.O在A的____________, O在B的____________,
0在C的____________, O在D的____________。
3.动手画一画某人在A处观望B在北偏东70°的方向上,则在B处观望A在B处的什么位置?
二、新知探究:【师生活动】学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
1、一艘船正以每小时30海里的速度由西向东追赶鱼群,在A处见小岛C在船的北偏东60°的方向上,已知小岛C为中心10海里的范围内有暗礁,船从A向东40分钟到B处看见小岛C在北偏东30°的方向,这艘船继续向东追赶鱼群有没有触礁的危险?
三、典例分析:【师生活动】 学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
1.某船以每小时36海里的速度向正东航行,在A点测得某岛C在北偏东60°的方向上,船行半小时后到B测得该岛在北偏东30°的方向上,已知该岛16海里内有暗礁
(1)试说明B点是否在暗礁区域外?
(2)若船继续向东航行,有无触礁危险?
四、题组训练: 【师生活动】 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
【A组】1、一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A地测得某灯塔位于它的北偏东30°的B处(如图1).上午9时行至C处,测得该灯塔恰好在它的正北方向,此时它与灯塔的距离是 海里(结果保留根号).
2、如图2所示,机器人从A点出发,沿着西南方向,行了个单位到达B点后,观察到原点O在它的南偏东60°的方向上,则A点的坐标为 (结果保留根号).
3、(图6-31)上午10点整,一渔轮在小岛O的北偏东30°方向,距离等于10海里的A处,以每小时10海里的速度向南偏东60°方向航行.那么渔轮到达小岛O的正东方向是什么时间?(精确到1分).
【B组】
4、.某货船以每小时20海里的速度将一批重要货物由A市运往正西方向的B市,经16小时到达B市,到B市后立即卸货,此时接到气象部门通知,一台风中心正以40海里每小时的速度有A向北偏西60°的方向上移动,距台风中心200海里的圆形区域会受到影响
(1)B市是否受到影响,说明理由
(2)若有影响,影响多长时间?
(3)为避免受到影响,该船应有多少小时内卸货?
【C组】(有能力同学完成)
5、在一次夏令营活动中,小明从营地A点出发,沿北偏东60°的方向走了50米到达B点,然后再沿北偏西30°的方向走了500米到达目的地C点
求A和C两地间的距离
确定目的地C在营地A的什么方向
答案:
知识链接:
北偏西45 南偏东45 北偏东45 南偏西45
南偏东45 北偏西45 南偏西45 北偏东45
南偏西70
新知探究
作CD⊥AB于D,
根据题意,AB=30×23=20(海里),∠CAD=30?,∠CBD=60?,
在Rt△ACD中,AD=CDtan30?=CD,
在Rt△BCD中,BD=CDtan60?=CD,
∵AB=AD?BD,
∴CD?CD=20(海里),
解得:CD=10>10,
所以不可能。
三、典例分析
(1)作CD⊥AB于D点,
设BC为x,
在Rt△BCD中∠CBD=60?,
∴BD=1/2x.
CD=x.
在Rt△ACD中∠CAD=30?tan∠CAD=CD/AD=,
∴
∴x=18.
∴点B是在暗礁区域外;
(2)∵CD==9,
∵9<16,
∴若继续向东航行船有触礁的危险。
四、题组训练
A组:1、 2、(0,) 3、11:44
B组:(1)如图,过点B作BD⊥AC交AC于点D,
∵在Rt△ABD中,∠BAC=90??60?=30?
∴BD=12AB
∵AB=20×16=320海里
∴BD=12×320=160海里。
∵160<200,
∴会受台风影响。
(2)在Rt△ADB中,AB=320海里,BD=160海里,则AD=160海里,
如图,BE=200海里,在Rt△BDE中,DE=120海里,
台风速度为40海里/小时,
故受影响的时间为:120×240=6(小时);
(3)要使卸货不受台风影响,则必须在点B距台风中心第一次为200海里前卸完货,
如图,BE=200海里,DE=120海里,
则AE=(160?120)海里,台风速度为40海里/小时,
则时间t=(160?120)/40=(4?3)≈4(小时),
答:为避免受到台风影响,该船应约在4小时内卸完货。
C组:(1)过B点作BE∥AD,
如图,∴∠DAB=∠ABE=60?.
∵30?+∠CBA+∠ABE=180?,∴∠CBA=90?.
即△ABC为直角三角形。
由已知可得:BC=500?m,AB=500?m,
由勾股定理可得:AC2=BC2+AB2,
所以AC=1?000(m);
(2)在Rt△ABC中,∵BC=500?m,AC=1?000?m,
∴∠CAB=30?,∵∠DAB=60?,∴∠DAC=30?.
即点C在点A的北偏东30?的方向。
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
