28.3.1圆心角-冀教版九年级数学上册导学案(含答案)
文档属性
| 名称 | 28.3.1圆心角-冀教版九年级数学上册导学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 70.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览

文档简介
九年级数学教案(编号40)
课题:圆心角 姓名
学习目标:1.理解圆心角的定义;2.探索圆心角的性质;
3.会用圆心角的性质解决问题
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
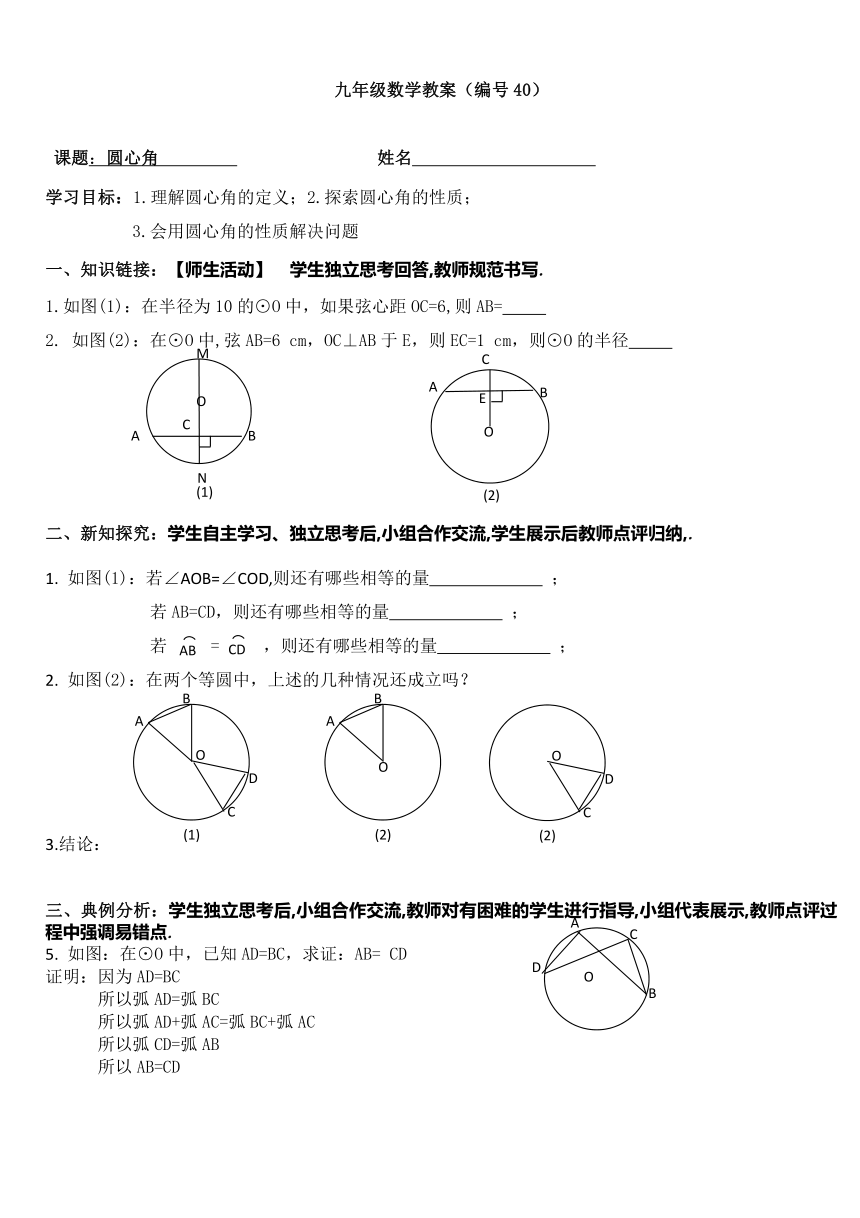
1.如图(1):在半径为10的⊙O中,如果弦心距OC=6,则AB=
2. 如图(2):在⊙O中,弦AB=6 cm,OC⊥AB于E,则EC=1 cm,则⊙O的半径
二、新知探究:学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
1. 如图(1):若∠AOB=∠COD,则还有哪些相等的量 ;
若AB=CD,则还有哪些相等的量 ;
若 = ,则还有哪些相等的量 ;
2. 如图(2):在两个等圆中,上述的几种情况还成立吗?
3.结论:
三、典例分析:学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
5. 如图:在⊙O中,已知AD=BC,求证:AB= CD
证明:因为AD=BC
所以弧AD=弧BC
所以弧AD+弧AC=弧BC+弧AC
所以弧CD=弧AB
所以AB=CD
四、题组训练: 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
【A组】
1.在⊙O1与⊙O2中,若∠AO1B=∠CO2D,则有( )
A B > C < D无法比较
2.如果两条弦相等,那么( )
A 这两条弦所对的弧相等 B 这两条弦所对的圆心角相等
C 这两条弦所对的圆的圆心到弦的距离相等 D以上说法都不对
3.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆心角的度数
4.一条弦把圆分成2:3两部分,那么这条弦所对的圆心角的度数
【B组】
5. 在⊙O中, 圆心角∠AOB=90o,点O到弦AB的距离为4,则⊙O的直径为( )
A 4 B 8 C 8 D 16
6.如图:已知 OA、OB、OC为⊙O的三条半径, 和 相等,M 、N分别为OA、OB的中点,求证:MC=CN
7.如图:在△AOB中,∠AOB=100o, ∠B=15o,以O为圆心,OA为半径的圆交AB于C,交OB于D,则 与 有什么关系?为什么?
答案:
知识链接:
16
5
新知探究
AB=CD
∠AOB=∠COD,
AB=CD ∠AOB=∠COD
相等
等弧 等弦 等角 知一推二
典例分析
作图略
四、题组训练
A组:
D
2、D
3、60度
4、114度
5、B
B组:
6、证明:∵OA、OB为O的半径,
∴OA=OB,
∵M是OA中点,N是OB中点,
∴OM=ON,(4分)
∵∠AOC=∠BOC,OC=OC,
∴△MOC≌△NOC,
∴MC=NC.
7、相等
课题:圆心角 姓名
学习目标:1.理解圆心角的定义;2.探索圆心角的性质;
3.会用圆心角的性质解决问题
一、知识链接:【师生活动】 学生独立思考回答,教师规范书写.
1.如图(1):在半径为10的⊙O中,如果弦心距OC=6,则AB=
2. 如图(2):在⊙O中,弦AB=6 cm,OC⊥AB于E,则EC=1 cm,则⊙O的半径
二、新知探究:学生自主学习、独立思考后,小组合作交流,学生展示后教师点评归纳,.
1. 如图(1):若∠AOB=∠COD,则还有哪些相等的量 ;
若AB=CD,则还有哪些相等的量 ;
若 = ,则还有哪些相等的量 ;
2. 如图(2):在两个等圆中,上述的几种情况还成立吗?
3.结论:
三、典例分析:学生独立思考后,小组合作交流,教师对有困难的学生进行指导,小组代表展示,教师点评过程中强调易错点.
5. 如图:在⊙O中,已知AD=BC,求证:AB= CD
证明:因为AD=BC
所以弧AD=弧BC
所以弧AD+弧AC=弧BC+弧AC
所以弧CD=弧AB
所以AB=CD
四、题组训练: 学生独立完成后小组交流答案,教师在巡视过程中帮助有困难的学生
【A组】
1.在⊙O1与⊙O2中,若∠AO1B=∠CO2D,则有( )
A B > C < D无法比较
2.如果两条弦相等,那么( )
A 这两条弦所对的弧相等 B 这两条弦所对的圆心角相等
C 这两条弦所对的圆的圆心到弦的距离相等 D以上说法都不对
3.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆心角的度数
4.一条弦把圆分成2:3两部分,那么这条弦所对的圆心角的度数
【B组】
5. 在⊙O中, 圆心角∠AOB=90o,点O到弦AB的距离为4,则⊙O的直径为( )
A 4 B 8 C 8 D 16
6.如图:已知 OA、OB、OC为⊙O的三条半径, 和 相等,M 、N分别为OA、OB的中点,求证:MC=CN
7.如图:在△AOB中,∠AOB=100o, ∠B=15o,以O为圆心,OA为半径的圆交AB于C,交OB于D,则 与 有什么关系?为什么?
答案:
知识链接:
16
5
新知探究
AB=CD
∠AOB=∠COD,
AB=CD ∠AOB=∠COD
相等
等弧 等弦 等角 知一推二
典例分析
作图略
四、题组训练
A组:
D
2、D
3、60度
4、114度
5、B
B组:
6、证明:∵OA、OB为O的半径,
∴OA=OB,
∵M是OA中点,N是OB中点,
∴OM=ON,(4分)
∵∠AOC=∠BOC,OC=OC,
∴△MOC≌△NOC,
∴MC=NC.
7、相等
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
