沪教版(上海)7年级寒假班06-三线八角及平行线的判定-教师版
文档属性
| 名称 | 沪教版(上海)7年级寒假班06-三线八角及平行线的判定-教师版 |

|
|
| 格式 | docx | ||
| 文件大小 | 761.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览



文档简介
1140460011772900初一数学寒假班(教师版)
教师
日期
学生
课程编号
06
课型
新课
课题
三线八角及平行线的判定
教学目标
1.理解和掌握三线八角的概念,明确三线八角只是位置关系没有数量关系;
2.理解和掌握平行线的概念及平行线的性质,并灵活运用;
3.理解和掌握平行线的判定定理,并能运用其进行简单的推理证明.
教学重点
1.理解和掌握三线八角的概念并运用;
2.理解和掌握平行线的判定并运用.
教学安排
版块
时长
1
三线八角的意义
20 min
2
平行线的意义和性质
15 min
3
平行线的判定
30 min
4
综合运用
25 min
5
随堂练习
30 min
84836051435三线八角及平行线的判定
三线八角及平行线的判定
-37147516510 知识结构
知识结构
267970179070模块一:三线八角的意义
模块一:三线八角的意义
-193040170180知识精讲
知识精讲
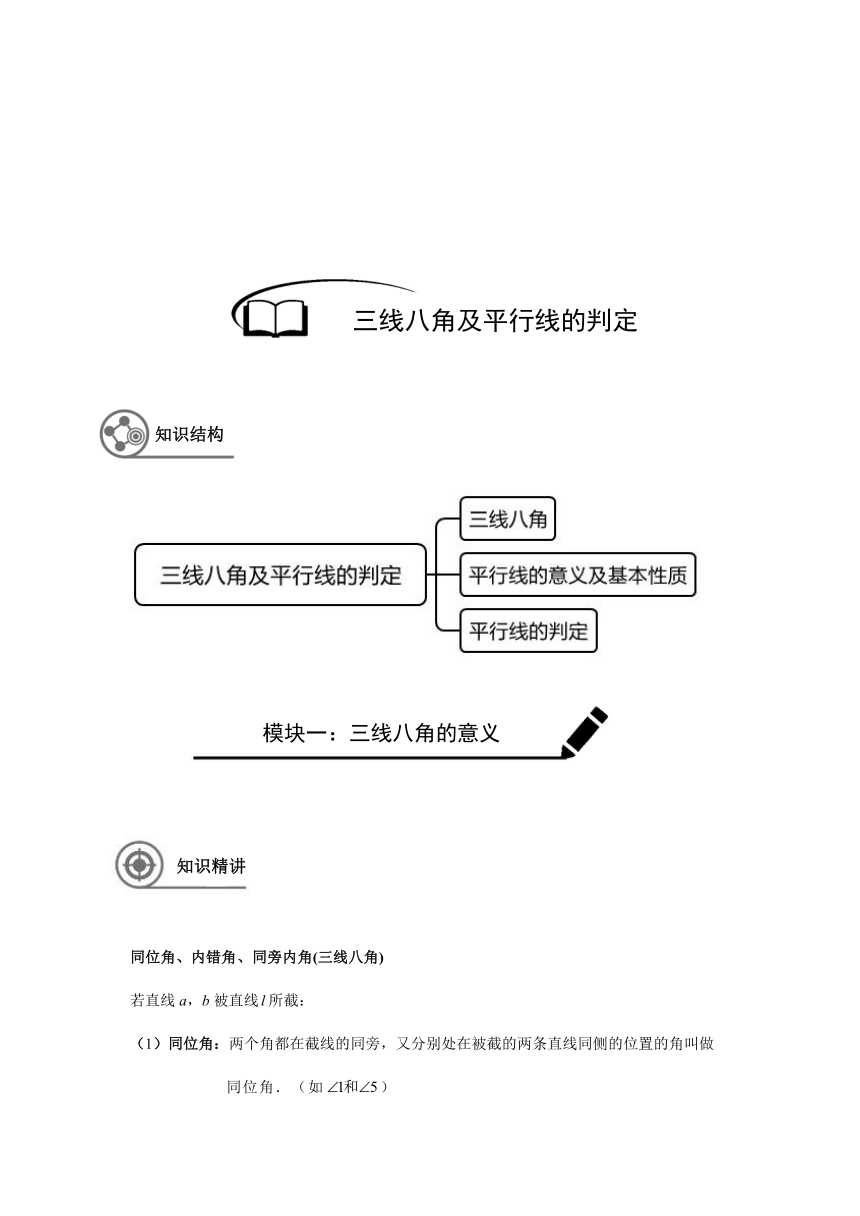
同位角、内错角、同旁内角(三线八角)
若直线a,b被直线false所截:
(1)同位角:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做
同位角.(如false)
(2)内错角:两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角
叫做内错角.(如false)
(3)同旁内角:两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的
368617513970false
false
false
1
2
3
4
5
6
7
8
false
false
false
1
2
3
4
5
6
7
8
一对角互为同旁内角.(如false)
注意:三线八角是位置关系,数量上没有确定的关系.
-60325150495例题解析
例题解析
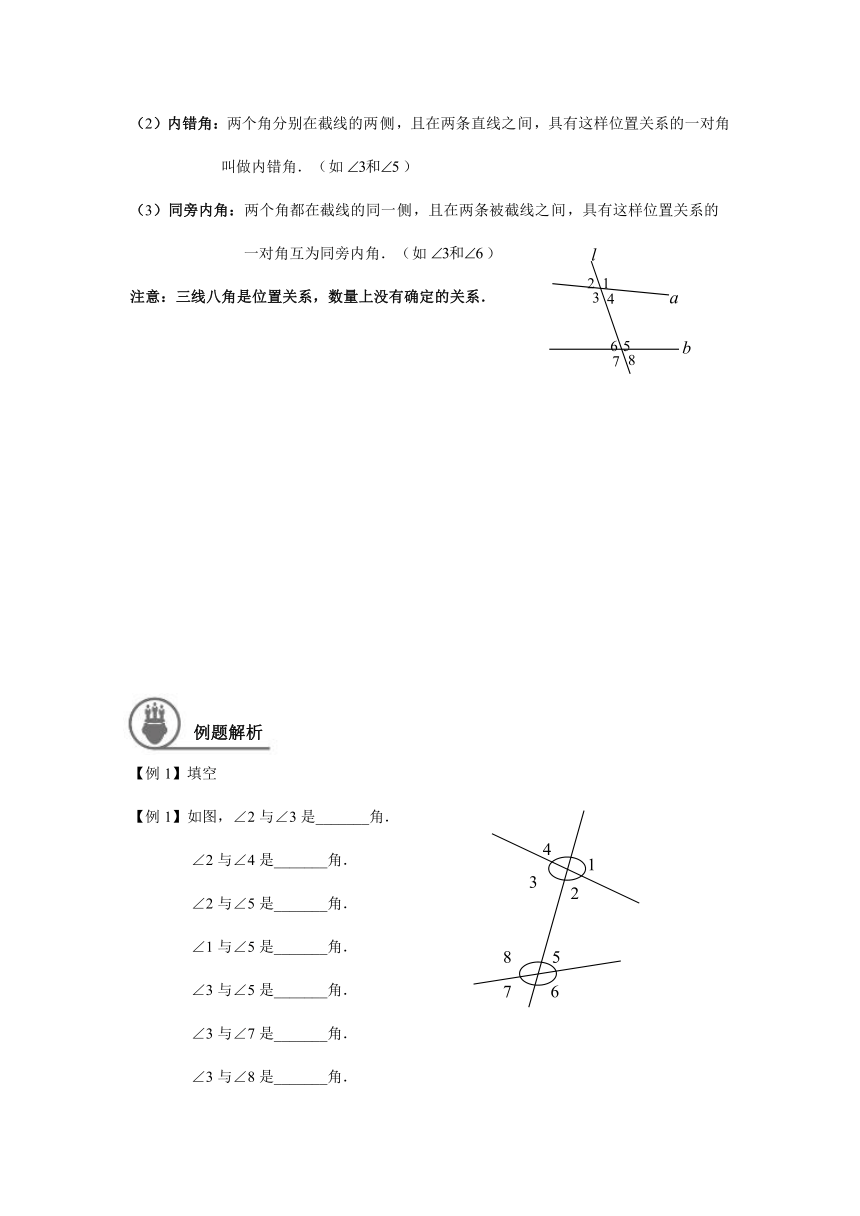
【例1】填空
30200601168401
2
3
4
8
7
6
5
1
2
3
4
8
7
6
5
【例1】如图,∠2与∠3是_______角.
∠2与∠4是_______角.
∠2与∠5是_______角.
∠1与∠5是_______角.
∠3与∠5是_______角.
∠3与∠7是_______角.
∠3与∠8是_______角.
∠2与∠8是_______角.
【难度】★
【答案】邻补角、对顶角、同旁内角、同位角、内错角、同位角、同旁内角、内错角.
【解析】考查线八角的角的概念.
【总结】考查三线八角的本概念.
【例2】填空
(1)∠B和∠1是两条直线________和_______被第三条直线_______所截构成的_______角.
(2)∠ACB与∠7是两条直线________和______被第三条直线______所截构成的_______角.
(3)∠3与∠5是两条直线________和______被第三条直线______所截构成的_______角.
(4)∠3与∠B是两条直线________和______被第三条直线______所截构成的_______角.
(5)∠2与∠7是两条直线________和______被第三条直线______所截构成的_______角.
42068756985A
B
C
D
E
A
B
C
D
E
【难度】★
【答案】(1)BC、DE、AB、同位角;(2)BC、DE、AC、同位角;
BA、CA、DC、内错角; (4)DC、BC、BA、同旁内角;
(5)DC、AC、DE、内错角.
【解析】考查线八角的角的概念.
【总结】考查三线八角的本概念.
3929380173355【例3】如图,同旁内角有( )对.
A.4对 B.3对 C.2对 D.1对
【难度】★
【答案】B
【解析】任意两个角都互为同旁内角,共3对.
【总结】考查同旁内角的概念.
【例4】如图,同位角共有( )对.
3653790215900A.1对 B.2对 C.3对 D.4对
【难度】★【答案】B
【解析】同位角像F形,由F形找同位角.
【总结】考查同位角的概念.
282892591268552
3
4
2
3
4
【例5】如图,是同位角关系的是( ).
A.∠3和∠4 B.∠1和∠4 C.∠2和∠4 D.不存在282892591268552
3
4
2
3
4
40017701225552
3
4
1
2
3
4
1
【难度】★【答案】B
【解析】A是内错角;B内错角;C同旁内角.
【总结】考查同位角的概念.
【例6】如图,内错角共有( )对.
A.1对 B.2对 C.3对 D.4对
348297526670A
B
C
E
F
D
A
B
C
E
F
D
【难度】★★【答案】D
【解析】∠EDB与∠DBC、∠EDB与∠DBA、
∠FDB与∠DBC、∠FDB与∠DBA,共4对
【总结】考查内错角的概念.
【例7】如图,同旁内角共有( )对.
A.10对 B.8对 C.6对 D.4对
365125019050A
B
C
E
F
D
A
B
C
E
F
D
【难度】★★【答案】C
【解析】四边形内有4组,四边形上方和右边各有一组,
共6组.
【总结】考查同旁内角的判定.
【例8】如图,∠1与∠2是两条直线____和____被第三条直线______所截构成的_____角.
∠3与∠4是两条直线________和______被第三条直线______所截构成的_______角.
339090093345A
B
C
D
A
B
C
D
【难度】★★
【答案】AD、BC、AC、内错角;AB、CD、AC、内错角.
【解析】内错角像字母Z.
【总结】考查内错角的特点及判定.
4038600540385A
B
C
D
E
1
2
A
B
C
D
E
1
2
【例9】 如图,∠C的同位角有_____________________,同旁内角是____________________, ∠1与∠2是___________角.直线AB和CD被AD所截,∠A的内错角是___________,
∠A与∠ADC是_______角.
【难度】★★
【答案】∠ADE、∠BDE;∠ABC、∠DBC、∠ADC、∠BDC;
内错角;∠ADE;同旁内角.
【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U.
【总结】考查基本角的特点.
【例10】如图,∠1的同位角是∠______,∠1的内错角是∠______,∠1的同旁内角是
∠_____, ∠1的对顶角是∠______,∠1的邻补角是∠______.
367411039370A
B
D
E
F
C
G
1
H
I
A
B
D
E
F
C
G
1
H
I
【难度】★★★
【答案】∠DEB、∠EBH;∠AEF、∠IBF;∠BEF、∠EBF;
∠CFG;∠CFD、∠GFH.
【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U,
找的时候要注意找全.
【总结】考查基本角的特点及概念.
3730625420370A
B
C
D
E
A
B
C
D
E
【例11】 如图,DC垂直于AE,已知∠DCE的同位角是它的一半,∠B=2∠ACB,试判断 △ABC的形状.
【难度】★★★
【答案】等腰直角三角形.
【解析】∵DC⊥AE,∴∠DCE=90°
∠DCE的同位角是∠BAC,由题已知∠BAC=45°,
∴∠B+∠ACB=180°-45°=135°
又∵∠B=2∠ACB ∴∠B=90°,∠ACB=45° ∴△ABC为等腰直角三角形
【总结】考查同位角的概念及三角形的类型判定.
503555101600模块二:平行线的意义和性质
模块二:平行线的意义和性质
-201930187325知识精讲
知识精讲
1、平行线的定义
同一平面内,不相交的两条直线叫平行线.
2、平行线的基本性质
(1)经过直线外一点,有且只有一条直线与已知直线平行;
(2)平行线之间的距离处处相等;
(3)平行于同一条直线的两直线平行(平行的传递性).
(4)同一平面内,垂直于同一条直线的两直线平行.
(5)两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值,这个定值叫做这两条平行线间的距离,平行线间的距离处处相等.
-133350108585例题解析
例题解析
【例12】已知直线false//false,false//false,那么false________false.
【难度】★【答案】平行
【解析】平行于同一条直线的两直线平行.
【总结】考查平行线的传递性.
【例13】a、b、c是直线,且a//b,b⊥c,则a与c的位置关系是________.
【难度】★【答案】垂直
【解析】∵a∥b,b⊥c,∴a⊥c.
【总结】考查直线的位置关系.
【例14】下列说法中,正确的是( ).
A.两直线不相交则平行 B.两直线不平行则相交
C.若两线段平行,那么它们不相交 D.两条线段不相交,那么它们平行
【难度】★【答案】C
【解析】两条直线还可能重合,所以A、B错;D错误.
【总结】考查同一平面内线段、直线的位置关系.
【例15】在同一平面内,有三条直线,其中只有两条是平行的,那么交点有( ).
A.0个 B.1个 C.2个 D.3个
【难度】★
【答案】C
【解析】第三条直线与这两条直线都相交,所以有两个交点.
【总结】考查直线的位置关系及交点个数.
【例16】下列说法中,错误的有( ).
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,那么a∥c;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种
A.3个 B.2个 C.1个 D.0个
【难度】★★【答案】A
【解析】①a与b可能平行,错误;②平行线的传递性,正确;③这个点必须不在已知直线
上,错误;④在同一平面内,两条直线的位置关系有平行、相交两种,错误.
【总结】考查同一平面内两直线的位置关系.
4328160156845M
M
3257550114300【例17】如图,按要求画平行线.
(1)过P点画AB的平行线EF;
(2)过P点画CD的平行线MN.
3004185166370E
E
4461510204470F
F
【难度】★★
3756660283845N
N
【答案】如右图.
【解析】如右图.
【总结】考查基本的作图能力.
3124200203200C
D
C
D
【例18】如图,点A,B分别在直线false,false上,
(1)过点A画到false的垂线段;
(2)过点B画直线CD∥false.
【难度】★★
【答案】如右图.
【解析】如右图.
【总结】考查基本的作图能力,此题中注意垂线段是一条线段,不要画成直线.
709295118745模块三:平行线的判定
模块三:平行线的判定
-7874092075知识精讲
知识精讲
平行线的三种判定方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
-76200161290例题解析
例题解析
392493513970
CB
A
B
D
E
CB
A
B
D
E
【例19】如图,请写出能判定CE∥AB的一个条件______________.
【难度】★【答案】∠DCE=∠A等.
【解析】可以通过同位角相等两直线平行来判定.
【总结】考查平行线的判定定理的运用,答案不唯一,只要成立即可.
【例20】如图,AB∥CD, AC⊥BC,∠BAC =65°,则∠BCD =_______度.
3651250171450A
B
C
D
E
A
B
C
D
E
【难度】★【答案】25°.
【解析】因为AB∥CD(已知),
所以false(两直线平行,内错角相等),
因为∠BAC =65°(已知), 所以false(等量代换).
因为AC⊥BC(已知), 所以false(垂直的意义)
因为false(邻补角的意义),
所以false(等式性质).
【总结】考查平行线的性质及邻补角性质的综合运用.
【例21】如图,下列说法错误的是( ).
38741351219201
2
3
4
5
6
1
2
3
4
5
6
A.∠1和∠3是同位角; B.∠1和∠5是同位角;
C.∠1和∠2是同旁内角; D.∠5和∠6是内错角.
【难度】★【答案】B
【解析】同位角像字母Z.
【总结】考查同位角的概念.
【例22】已知,△ABC中,DE垂直于AC于E,∠ACB=90°,试说明DE∥BC的理由.
3995420128270A
B
C
D
E
A
B
C
D
E
【难度】★★【答案】略.
【解析】因为DE⊥AC(已知),
所以false(垂直的意义).
因为∠ACB=90°(已知),所以∠ACB=∠AED(等量代换),
所以DE∥BC(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的意义的综合运用.
【例23】如图,∠5=∠CDA =∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
316547566675A
B
C
D
E
A
B
C
D
E
∵∠5=∠CDA(已知)
∴_______//_______(内错角相等,两直线平行)
∵∠5=∠ABC(已知)
∴_______//_______(同位角相等,两直线平行)
∵∠2=∠3(已知)
∴_______//_______(内错角相等,两直线平行)
∵∠BAD+∠CDA=180°(已知)
∴_______//_______(同旁内角互补,两直线平行)
∵∠5=∠CDA(已知),
又∵∠5与∠BCD互补,∠CDA与_______互补(邻补角定义)
∴∠BCD=∠6(等角的补角相等)
∴_______//_______(同位角相等,两直线平行)
【难度】★★
【答案】AD、BC;AB、CD;AB、CD;AB、CD;∠6;AD、BC.
【解析】解题时要看清题目,根据条件判断出哪一组直线平行,不能混淆.
【总结】考查平行线的判定定理的运用.
4092575245745A
B
C
D
E
F
A
B
C
D
E
F
【例24】如图,AB⊥BC,∠1+∠2=90°,∠2=∠3,那么BE与DF平行吗?为什么?
【难度】★★
【答案】平行
【解析】因为AB⊥BC(已知),
所以∠ABC=90°(垂直的意义),即false(角的和差)
因为∠2=∠3(已知), 所以false(等量代换)
因为∠1+∠2=90°(已知), 所以∠1=∠4(同角的余角相等),
所以BE∥DF(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的综合运用,注意分析题目中条件.
3803650-8255A
B
C
D
E
F
1
2
3
A
B
C
D
E
F
1
2
3
【例25】如图,∠2=3∠1,且∠1+∠3=90°,试说明false.
【难度】★★【答案】略
【解析】因为∠2=3∠1(已知),∠2+∠1=180°(邻补角的意义),
所以∠1=45°,∠2=135°(等式性质).
又因为∠1+∠3=90°(已知),
所以∠3=45°(等式性质), 所以∠2+∠3=180°(等式性质),
所以AB∥CD(同旁内角互补,两直线平行)
【总结】考查平行线的判定定理的运用.
【例26】已知∠1=∠2,DE平分∠BDC,DE交AB于点E,试说明AB//CD.
302260036830A
B
C
D
E
F
G
2
1
A
B
C
D
E
F
G
2
1
【难度】★★【答案】略.
【解析】因为DE平分∠BDC(已知),
所以∠2=∠EDC(角平分线的意义)
因为∠1=∠2(已知),
所以∠1=∠EDC(等量代换)
所以AB∥CD(内错角相等,两直线平行)
【总结】考查平行线的判定定理及角平分线的意义的综合运用.
【例27】 已知AC、BC分别平分∠QAB、∠ABN,且∠1与∠2互余,试说明PQ//MN.
351028092075A
B
C
P
Q
M
N
2
1
A
B
C
P
Q
M
N
2
1
【难度】★★
【答案】略
【解析】因为AC、BC分别平分∠QAB、∠ABN(已知)
所以∠1=false∠QAB,∠2=false∠ABN(角平分线的意义)
因为∠1+∠2=90°(互余的意义)
所以∠QAB+∠ABN=180°(等式性质) 所以PQ∥MN(同旁内角互补,两直线平行)
【总结】考查平行线的判定及角平分线的意义的综合运用,注意分析条件,得出角度间的关系.
3619500381000A
B
C
D
E
F
G
H
O
A
B
C
D
E
F
G
H
O
【例28】如图,直线AB分别与直线CD、EF交于点O、点E,GO⊥OH,OH平分∠AOC,
且∠EDO与∠GOB互余,试说明OH //EF.
【难度】★★★【答案】略
【解析】因为GO⊥OH(已知),
所以false(垂直的意义),
因为OH平分∠AOC(已知),
所以false(角平分线的意义).
因为false(邻补角的意义),所以∠GOB+∠HOC=90°(等式性质)
因为∠EDO+∠GOB=90°(已知)所以∠EDO=∠HOC (同角的余角相等)
所以OH∥EF(同位角相等,两直线平行)
【总结】本题综合性较强,主要考查平行线的判定定理及同角的余角相等的综合运用,解题时认真分析,找出角度间的关系.
3422650174625A
B
C
D
E
A
B
C
D
E
【例29】如图,∠ABE=∠E+∠D,试说明AB//CD的理由.
【难度】★★★【答案】略
【解析】因为false(三角形内角和等于180°)
又false(邻补角的意义)
所以∠DCB=∠E+∠D(等式性质)
因为∠ABE=∠E+∠D(已知)
所以∠DCB=∠ABE(等量代换),
所以AB∥CD(内错角相等,两直线平行)
【总结】考查平行线的判定定理及三角形内角和的综合运用,综合性较强,解题时要认真分析.
-101600111760随堂检测
随堂检测
【习题1】27025602508251
7
3
5
6
2
4
1
7
3
5
6
2
4
观察图,下列说法中,正确的是( ).
A.false和false是内错角
B.false和false是同位角
C.false和false是内错角
D.false和false是同旁内角
【难度】★【答案】D
【解析】考查同位角、内错角和同旁内角的概念及判定.
3422650165100A
B
C
D
E
A
B
C
D
E
【习题2】如图,能使AB∥CD的条件是( ).
∠1=∠B B.∠3=∠A
C.∠1+∠2+∠B=180° D.∠1=∠A
【难度】★【答案】C
【解析】同旁内角互补,两直线平行,C选项满足条件.
【总结】考查平行线的判定定理的运用.
【习题3】一学员在广场上练习驾车,两次拐弯后,行驶的方向与原来的方向相同,这两次 拐弯的角度是( )
A.第一次向左拐,第二次向右拐
B.第一次向右拐,第二次向左拐
C.第一次向右拐,第二次向右拐
D.第一次向左拐,第二次向左拐
【难度】★【答案】A
【解析】B向左拐了50°,C、D都朝相反方向开去.
【总结】考查平行线的判定定理在实际问题中的运用.
【习题4】如图,在下列条件中,能判定AB//CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
361886533020A
B
C
D
A
B
C
D
【难度】★
【答案】C
【解析】A错误;B能推出AD∥BD;D错误.
【总结】考查平行线的判定定理的运用.
3238500600075【习题5】如图,图中所标号的8个角,是∠1的同位角的是_________;∠3的内错角是 _________;∠7的同旁内角是_________;∠4的同位角是_________;∠6的内错角是 _________;∠2的同旁内角是_________.
【难度】★
【答案】∠2;∠5;∠6、∠8;∠3、∠7;
∠4;∠5.
【解析】考查同位角、内错角、同旁内角的概念.
3455670278765【习题6】如图,已知直线b⊥a,c⊥a.那么直线b与c平行吗?如果平行,请给出证明; 如果不平行,举出反例.
【难度】★★
【答案】平行.
【解析】因为b⊥a,c⊥a(已知),
∴∠1=∠2=90°(垂直的意义),
∴b∥c(同位角相等,两直线平行).
【总结】考查平行线的判定定理及垂直的意义的综合运用.
【习题7】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF
2495550136525A
B
C
D
E
F
1
2
N
M
A
B
C
D
E
F
1
2
N
M
平行吗?为什么?
【难度】★★
【答案】平行.
【解析】因为∠1=35°,∠2=35°(已知),
所以∠1=∠2(等量代换),
因为AC⊥AE,BD⊥BF(已知), 所以false(垂直的意义)
所以∠NBF=∠BAE(等式性质)
所以AE∥BF(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的意义的综合运用.
53079653480435
【习题8】如图,∠1+∠2=180°.AE与FC会平行吗? 说明理由.
【难度】★★【答案】平行.
【解析】因为∠1+∠2=180°(已知),∠2+∠BDC=180°(邻补角的意义)
所以∠1=∠BDC(同角的补角相等)
所以CF∥AE(同位角相等,两直线平行)
【总结】考查平行线的判定定理的运用.
【习题9】根据图完成下列填空(括号内填写定理或公理)
(1)∵∠1=∠4(已知)
∴_________∥_________( )
(2)∵∠ABC +∠_________=180°(已知)
3178810156210A
B
C
D
E
A
B
C
D
E
∴AB∥CD( )
(3)∵∠_________=∠_________(已知)
∴AD∥BC( )
(4)∵∠5=∠_________(已知)
∴AB∥CD( )
【难度】★★
【答案】(1)AB∥CD、内错角相等,两直线平行;
(2)∠BCD、同旁内角互补,两直线平行;
(3)∠2=∠3、内错角相等,两直线平行;
(4)∠ABC、同位角相等,两直线平行.
【解析】考查平行线的判定定理的综合运用.
3365500212090B
C
D
E
F
G
H
B
C
D
E
F
G
H
【习题10】已知DE⊥BC,FG⊥BC,∠DEH=∠GFC,试说明EH∥FC的理由.
【难度】★★
【答案】略.
【解析】因为DE⊥BC,FG⊥BC(已知)
所以∠DEC=∠FGC=90°(垂直的意义)
所以∠GFC+∠FCG=90°(三角形内角和等于180°)
因为∠DEH=∠GFC(已知), 所以∠HEC=∠FCG(等角的余角相等)
所以EH∥FC(内错角相等,两直线平行)
【总结】考查平行线的判定定理的运用.
【习题11】 已知∠EDC+∠B=180°,∠EDC=∠A,试说明AE//BC的理由.
347027538100A
B
C
D
E
A
B
C
D
E
【难度】★★【答案】略
【解析】因为∠EDC+∠B=180°,∠EDC=∠A(已知)
所以∠A+∠B=180°(等量代换)
所以AE∥BC(同旁内角互补,两直线平行)
【总结】考查平行线的判定定理的运用.
【习题12】已知:∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,false.
357505093980A
B
C
D
E
F
A
B
C
D
E
F
试说明DE∥BF的理由.
【难度】★★
【答案】略
【解析】因为BF和DE分别平分∠ABC和∠ADC(已知)
所以false,false(角平分线的意义)
因为∠ABC=∠ADC(已知),所以∠1=∠ABF(等式性质)
因为∠1=∠2(已知), ∴∠2=∠FBA(等量代换)
所以DE∥BF(同位角相等,两直线平行)
3710940123190a
b
c
d
a
b
c
d
【总结】考查平行线的判定定理及角平分线意义的综合运用.
【习题13】已知直线a,b,c被直线d所截,false,试说明a∥c.
【难度】★★【答案】略.
【解析】因为∠1=∠3(已知)
所以a∥b(同位角相等,两直线平行)
因为∠3+∠4=180°(已知),∠3+∠5=180°(邻补角的意义)
所以∠4=∠5(同角的补角相等) 所以b∥c(同位角相等,两直线平行)
所以a∥c(平行的传递性)
【总结】考查平行线的判定定理及平行的传递性的综合运用.
-247650146685课后作业
课后作业
【作业1】下列说法中正确的是( )
A.经过一点,有且只有一条直线与已知直线平行
B.两条直线被第三条直线所截,同位角相等
C.垂直于同一条直线的两条直线互相垂直
D.两条直线被第三条直线所截,内错角相等,则两条直线平行
【难度】★【答案】D
【解析】A这个点必须是直线外的点,错误;B同位角相等的前提是两直线平行,错误;
C垂直于同一条直线的两条直线互相平行,错误;故选D
【总结】考查平面内直线的位置关系.
【作业2】在同一平面内,若a⊥b,c⊥b则a与c的关系是( )
A.平行 B.垂直 C.相交 D.以上都不对
【难度】★【答案】A
【解析】垂直于同一条直线的两条直线互相平行
【总结】考查平面内直线的位置关系.
3740150203200【作业3】如图,∠ADE和∠CED是( )
A.同位角 B.内错角 C.同旁内角 D.互为补角
【难度】★【答案】B
【解析】内错角像字母Z.
【总结】考查内错角的特点及判定.
3100070184150【作业4】如图,属于内错角的是( )
A.∠1和∠2 B.∠2和∠3
C.∠1和∠4 D.∠3和∠4
【难度】★
【答案】D
【解析】内错角像字母Z.
【总结】考查基本角的特点.
【作业5】11430006243320
下列有关垂直相交的说法:
①同一平面内,垂直于同一条直线的两条直线互相平行;
②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;
③同一平面内, 一条直线不可能与两条相交直线都垂直;
其中说法正确个数有( )
A.3个 B.2个 C.1个 D.0个
【难度】★★【答案】B
【解析】①、③正确,②要在同一平面内才成立,故选C.
【总结】考查平面内直线的位置关系.
【作业6】下列语句:①三条直线只有两个交点,则其中两条直线互相平行;
②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题 B.②、③是正确命题
C.①、③是正确命题 D.以上结论皆错
【难度】★★【答案】A
【解析】①正确;②两直线平行,同旁内角互补,此时又相等,所以两个角分别为90°,
即垂直,正确;③这个点必须是直线外的一点,错误,故选A.
【总结】考查平面内直线的位置关系.
【作业7】如图,能与false构成同旁内角的角有( )
falseA.5个 B.4个
C.3个 D.2个
【难度】★★【答案】A
【解析】同旁内角像字母U
【总结】考查基本角的特点及判定.
【作业8】如图,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
366712595250(1)判断CD与AB的位置关系;
(2)BE与DF平行吗?为什么?
【难度】★★
【答案】(1)平行 (2)平行
【解析】(1)因为AB⊥BD,CD⊥MN(已知),
所以CD∥AB(垂直于同一条直线的两条直线互相平行);
(2)因为∠CDM=∠ABMfalse(垂直的意义),又∠FDC=∠EBA(已知),
所以∠MDF=∠MBE(等式性质)
所以BE∥DF(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的综合运用.
3670300139700A
B
C
D
E
F
G
A
B
C
D
E
F
G
【作业9】 如图CD⊥AB,EF⊥AB,∠1=∠2,试说明DG//BC的理由.
【难度】★★
【答案】略
【解析】因为CD⊥AB,EF⊥AB(已知),
所以EF∥CD(垂直于同一条直线的两条直线互相平行)
所以∠2=∠DCB(两直线平行,同位角相等)
因为∠2=∠1(已知), 所以∠1=∠DCB(等量代换)
所以DG∥BC(内错角相等,两直线平行)
【总结】考查平行线的判定定理及性质定理的综合运用.
3514725209550【作业10】如图,AB、CD被EF所截,MG平分∠BMN,NH平分∠DNM,
已知∠GMN+∠HNM=90°,试问:AB∥CD吗?请说明理由.
【难度】★★★
【答案】平行.
【解析】因为MG平分∠BMN,NH平分∠DNM(已知)
所以∠BMN=2∠GMN,∠DNM=2∠HNM(角平分线的意义)
因为∠FMG+∠HNM=90°(已知)
所以∠BMN+∠DNM=180°(等式性质)
所以AB∥CD(同旁内角互补,两直线平行)
【总结】考查平行线的判定定理及角平分线的综合运用.
3679190163195A
B
C
D
E
F
A
B
C
D
E
F
【作业11】 如图, ∠B=∠C,∠A=∠D,试说明AE//DF.
【难度】★★★
【答案】略
【解析】因为false,false(三角形内角和等于180°)
又false,false(邻补角的意义)
所以false,false(等式性质)
因为∠B=∠C,∠A=∠D(已知), 所以false(等式性质),
所以AE∥DF(内错角相等,两直线平行)
【总结】考查平行线的判定定理及三角形内角和定理的综合运用,综合性较强,建议老师选择性讲解.
【作业12】如图,已知:∠B+∠D=∠BED.AB与CD平行吗,说明理由.
353377573025A
B
C
D
E
F
A
B
C
D
E
F
【难度】★★★
【答案】略
【解析】过点E作EF∥AB,
则∠B=∠BEF(两直线平行,内错角相等)
因为∠BED =∠BEF+∠FED =∠B+∠D(已知),
所以∠FED=∠D(等式性质)
所以CD∥EF(内错角相等,两直线平行)
所以AB∥CD(平行的传递性)
【总结】考查平行线的判定定理及性质定理的综合运用,教师可选择性的讲解.
教师
日期
学生
课程编号
06
课型
新课
课题
三线八角及平行线的判定
教学目标
1.理解和掌握三线八角的概念,明确三线八角只是位置关系没有数量关系;
2.理解和掌握平行线的概念及平行线的性质,并灵活运用;
3.理解和掌握平行线的判定定理,并能运用其进行简单的推理证明.
教学重点
1.理解和掌握三线八角的概念并运用;
2.理解和掌握平行线的判定并运用.
教学安排
版块
时长
1
三线八角的意义
20 min
2
平行线的意义和性质
15 min
3
平行线的判定
30 min
4
综合运用
25 min
5
随堂练习
30 min
84836051435三线八角及平行线的判定
三线八角及平行线的判定
-37147516510 知识结构
知识结构
267970179070模块一:三线八角的意义
模块一:三线八角的意义
-193040170180知识精讲
知识精讲
同位角、内错角、同旁内角(三线八角)
若直线a,b被直线false所截:
(1)同位角:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做
同位角.(如false)
(2)内错角:两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角
叫做内错角.(如false)
(3)同旁内角:两个角都在截线的同一侧,且在两条被截线之间,具有这样位置关系的
368617513970false
false
false
1
2
3
4
5
6
7
8
false
false
false
1
2
3
4
5
6
7
8
一对角互为同旁内角.(如false)
注意:三线八角是位置关系,数量上没有确定的关系.
-60325150495例题解析
例题解析
【例1】填空
30200601168401
2
3
4
8
7
6
5
1
2
3
4
8
7
6
5
【例1】如图,∠2与∠3是_______角.
∠2与∠4是_______角.
∠2与∠5是_______角.
∠1与∠5是_______角.
∠3与∠5是_______角.
∠3与∠7是_______角.
∠3与∠8是_______角.
∠2与∠8是_______角.
【难度】★
【答案】邻补角、对顶角、同旁内角、同位角、内错角、同位角、同旁内角、内错角.
【解析】考查线八角的角的概念.
【总结】考查三线八角的本概念.
【例2】填空
(1)∠B和∠1是两条直线________和_______被第三条直线_______所截构成的_______角.
(2)∠ACB与∠7是两条直线________和______被第三条直线______所截构成的_______角.
(3)∠3与∠5是两条直线________和______被第三条直线______所截构成的_______角.
(4)∠3与∠B是两条直线________和______被第三条直线______所截构成的_______角.
(5)∠2与∠7是两条直线________和______被第三条直线______所截构成的_______角.
42068756985A
B
C
D
E
A
B
C
D
E
【难度】★
【答案】(1)BC、DE、AB、同位角;(2)BC、DE、AC、同位角;
BA、CA、DC、内错角; (4)DC、BC、BA、同旁内角;
(5)DC、AC、DE、内错角.
【解析】考查线八角的角的概念.
【总结】考查三线八角的本概念.
3929380173355【例3】如图,同旁内角有( )对.
A.4对 B.3对 C.2对 D.1对
【难度】★
【答案】B
【解析】任意两个角都互为同旁内角,共3对.
【总结】考查同旁内角的概念.
【例4】如图,同位角共有( )对.
3653790215900A.1对 B.2对 C.3对 D.4对
【难度】★【答案】B
【解析】同位角像F形,由F形找同位角.
【总结】考查同位角的概念.
282892591268552
3
4
2
3
4
【例5】如图,是同位角关系的是( ).
A.∠3和∠4 B.∠1和∠4 C.∠2和∠4 D.不存在282892591268552
3
4
2
3
4
40017701225552
3
4
1
2
3
4
1
【难度】★【答案】B
【解析】A是内错角;B内错角;C同旁内角.
【总结】考查同位角的概念.
【例6】如图,内错角共有( )对.
A.1对 B.2对 C.3对 D.4对
348297526670A
B
C
E
F
D
A
B
C
E
F
D
【难度】★★【答案】D
【解析】∠EDB与∠DBC、∠EDB与∠DBA、
∠FDB与∠DBC、∠FDB与∠DBA,共4对
【总结】考查内错角的概念.
【例7】如图,同旁内角共有( )对.
A.10对 B.8对 C.6对 D.4对
365125019050A
B
C
E
F
D
A
B
C
E
F
D
【难度】★★【答案】C
【解析】四边形内有4组,四边形上方和右边各有一组,
共6组.
【总结】考查同旁内角的判定.
【例8】如图,∠1与∠2是两条直线____和____被第三条直线______所截构成的_____角.
∠3与∠4是两条直线________和______被第三条直线______所截构成的_______角.
339090093345A
B
C
D
A
B
C
D
【难度】★★
【答案】AD、BC、AC、内错角;AB、CD、AC、内错角.
【解析】内错角像字母Z.
【总结】考查内错角的特点及判定.
4038600540385A
B
C
D
E
1
2
A
B
C
D
E
1
2
【例9】 如图,∠C的同位角有_____________________,同旁内角是____________________, ∠1与∠2是___________角.直线AB和CD被AD所截,∠A的内错角是___________,
∠A与∠ADC是_______角.
【难度】★★
【答案】∠ADE、∠BDE;∠ABC、∠DBC、∠ADC、∠BDC;
内错角;∠ADE;同旁内角.
【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U.
【总结】考查基本角的特点.
【例10】如图,∠1的同位角是∠______,∠1的内错角是∠______,∠1的同旁内角是
∠_____, ∠1的对顶角是∠______,∠1的邻补角是∠______.
367411039370A
B
D
E
F
C
G
1
H
I
A
B
D
E
F
C
G
1
H
I
【难度】★★★
【答案】∠DEB、∠EBH;∠AEF、∠IBF;∠BEF、∠EBF;
∠CFG;∠CFD、∠GFH.
【解析】同位角像字母F,内错角像字母Z,同旁内角像字母U,
找的时候要注意找全.
【总结】考查基本角的特点及概念.
3730625420370A
B
C
D
E
A
B
C
D
E
【例11】 如图,DC垂直于AE,已知∠DCE的同位角是它的一半,∠B=2∠ACB,试判断 △ABC的形状.
【难度】★★★
【答案】等腰直角三角形.
【解析】∵DC⊥AE,∴∠DCE=90°
∠DCE的同位角是∠BAC,由题已知∠BAC=45°,
∴∠B+∠ACB=180°-45°=135°
又∵∠B=2∠ACB ∴∠B=90°,∠ACB=45° ∴△ABC为等腰直角三角形
【总结】考查同位角的概念及三角形的类型判定.
503555101600模块二:平行线的意义和性质
模块二:平行线的意义和性质
-201930187325知识精讲
知识精讲
1、平行线的定义
同一平面内,不相交的两条直线叫平行线.
2、平行线的基本性质
(1)经过直线外一点,有且只有一条直线与已知直线平行;
(2)平行线之间的距离处处相等;
(3)平行于同一条直线的两直线平行(平行的传递性).
(4)同一平面内,垂直于同一条直线的两直线平行.
(5)两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值,这个定值叫做这两条平行线间的距离,平行线间的距离处处相等.
-133350108585例题解析
例题解析
【例12】已知直线false//false,false//false,那么false________false.
【难度】★【答案】平行
【解析】平行于同一条直线的两直线平行.
【总结】考查平行线的传递性.
【例13】a、b、c是直线,且a//b,b⊥c,则a与c的位置关系是________.
【难度】★【答案】垂直
【解析】∵a∥b,b⊥c,∴a⊥c.
【总结】考查直线的位置关系.
【例14】下列说法中,正确的是( ).
A.两直线不相交则平行 B.两直线不平行则相交
C.若两线段平行,那么它们不相交 D.两条线段不相交,那么它们平行
【难度】★【答案】C
【解析】两条直线还可能重合,所以A、B错;D错误.
【总结】考查同一平面内线段、直线的位置关系.
【例15】在同一平面内,有三条直线,其中只有两条是平行的,那么交点有( ).
A.0个 B.1个 C.2个 D.3个
【难度】★
【答案】C
【解析】第三条直线与这两条直线都相交,所以有两个交点.
【总结】考查直线的位置关系及交点个数.
【例16】下列说法中,错误的有( ).
①若a与c相交,b与c相交,则a与b相交;
②若a∥b,b∥c,那么a∥c;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种
A.3个 B.2个 C.1个 D.0个
【难度】★★【答案】A
【解析】①a与b可能平行,错误;②平行线的传递性,正确;③这个点必须不在已知直线
上,错误;④在同一平面内,两条直线的位置关系有平行、相交两种,错误.
【总结】考查同一平面内两直线的位置关系.
4328160156845M
M
3257550114300【例17】如图,按要求画平行线.
(1)过P点画AB的平行线EF;
(2)过P点画CD的平行线MN.
3004185166370E
E
4461510204470F
F
【难度】★★
3756660283845N
N
【答案】如右图.
【解析】如右图.
【总结】考查基本的作图能力.
3124200203200C
D
C
D
【例18】如图,点A,B分别在直线false,false上,
(1)过点A画到false的垂线段;
(2)过点B画直线CD∥false.
【难度】★★
【答案】如右图.
【解析】如右图.
【总结】考查基本的作图能力,此题中注意垂线段是一条线段,不要画成直线.
709295118745模块三:平行线的判定
模块三:平行线的判定
-7874092075知识精讲
知识精讲
平行线的三种判定方法:
两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单地说,同位角相等,两直线平行.
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
简单地说,内错角相等,两直线平行.
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
简单地说,同旁内角互补,两直线平行.
-76200161290例题解析
例题解析
392493513970
CB
A
B
D
E
CB
A
B
D
E
【例19】如图,请写出能判定CE∥AB的一个条件______________.
【难度】★【答案】∠DCE=∠A等.
【解析】可以通过同位角相等两直线平行来判定.
【总结】考查平行线的判定定理的运用,答案不唯一,只要成立即可.
【例20】如图,AB∥CD, AC⊥BC,∠BAC =65°,则∠BCD =_______度.
3651250171450A
B
C
D
E
A
B
C
D
E
【难度】★【答案】25°.
【解析】因为AB∥CD(已知),
所以false(两直线平行,内错角相等),
因为∠BAC =65°(已知), 所以false(等量代换).
因为AC⊥BC(已知), 所以false(垂直的意义)
因为false(邻补角的意义),
所以false(等式性质).
【总结】考查平行线的性质及邻补角性质的综合运用.
【例21】如图,下列说法错误的是( ).
38741351219201
2
3
4
5
6
1
2
3
4
5
6
A.∠1和∠3是同位角; B.∠1和∠5是同位角;
C.∠1和∠2是同旁内角; D.∠5和∠6是内错角.
【难度】★【答案】B
【解析】同位角像字母Z.
【总结】考查同位角的概念.
【例22】已知,△ABC中,DE垂直于AC于E,∠ACB=90°,试说明DE∥BC的理由.
3995420128270A
B
C
D
E
A
B
C
D
E
【难度】★★【答案】略.
【解析】因为DE⊥AC(已知),
所以false(垂直的意义).
因为∠ACB=90°(已知),所以∠ACB=∠AED(等量代换),
所以DE∥BC(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的意义的综合运用.
【例23】如图,∠5=∠CDA =∠ABC,∠1=∠4,∠2=∠3,∠BAD+∠CDA=180°,填空:
316547566675A
B
C
D
E
A
B
C
D
E
∵∠5=∠CDA(已知)
∴_______//_______(内错角相等,两直线平行)
∵∠5=∠ABC(已知)
∴_______//_______(同位角相等,两直线平行)
∵∠2=∠3(已知)
∴_______//_______(内错角相等,两直线平行)
∵∠BAD+∠CDA=180°(已知)
∴_______//_______(同旁内角互补,两直线平行)
∵∠5=∠CDA(已知),
又∵∠5与∠BCD互补,∠CDA与_______互补(邻补角定义)
∴∠BCD=∠6(等角的补角相等)
∴_______//_______(同位角相等,两直线平行)
【难度】★★
【答案】AD、BC;AB、CD;AB、CD;AB、CD;∠6;AD、BC.
【解析】解题时要看清题目,根据条件判断出哪一组直线平行,不能混淆.
【总结】考查平行线的判定定理的运用.
4092575245745A
B
C
D
E
F
A
B
C
D
E
F
【例24】如图,AB⊥BC,∠1+∠2=90°,∠2=∠3,那么BE与DF平行吗?为什么?
【难度】★★
【答案】平行
【解析】因为AB⊥BC(已知),
所以∠ABC=90°(垂直的意义),即false(角的和差)
因为∠2=∠3(已知), 所以false(等量代换)
因为∠1+∠2=90°(已知), 所以∠1=∠4(同角的余角相等),
所以BE∥DF(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的综合运用,注意分析题目中条件.
3803650-8255A
B
C
D
E
F
1
2
3
A
B
C
D
E
F
1
2
3
【例25】如图,∠2=3∠1,且∠1+∠3=90°,试说明false.
【难度】★★【答案】略
【解析】因为∠2=3∠1(已知),∠2+∠1=180°(邻补角的意义),
所以∠1=45°,∠2=135°(等式性质).
又因为∠1+∠3=90°(已知),
所以∠3=45°(等式性质), 所以∠2+∠3=180°(等式性质),
所以AB∥CD(同旁内角互补,两直线平行)
【总结】考查平行线的判定定理的运用.
【例26】已知∠1=∠2,DE平分∠BDC,DE交AB于点E,试说明AB//CD.
302260036830A
B
C
D
E
F
G
2
1
A
B
C
D
E
F
G
2
1
【难度】★★【答案】略.
【解析】因为DE平分∠BDC(已知),
所以∠2=∠EDC(角平分线的意义)
因为∠1=∠2(已知),
所以∠1=∠EDC(等量代换)
所以AB∥CD(内错角相等,两直线平行)
【总结】考查平行线的判定定理及角平分线的意义的综合运用.
【例27】 已知AC、BC分别平分∠QAB、∠ABN,且∠1与∠2互余,试说明PQ//MN.
351028092075A
B
C
P
Q
M
N
2
1
A
B
C
P
Q
M
N
2
1
【难度】★★
【答案】略
【解析】因为AC、BC分别平分∠QAB、∠ABN(已知)
所以∠1=false∠QAB,∠2=false∠ABN(角平分线的意义)
因为∠1+∠2=90°(互余的意义)
所以∠QAB+∠ABN=180°(等式性质) 所以PQ∥MN(同旁内角互补,两直线平行)
【总结】考查平行线的判定及角平分线的意义的综合运用,注意分析条件,得出角度间的关系.
3619500381000A
B
C
D
E
F
G
H
O
A
B
C
D
E
F
G
H
O
【例28】如图,直线AB分别与直线CD、EF交于点O、点E,GO⊥OH,OH平分∠AOC,
且∠EDO与∠GOB互余,试说明OH //EF.
【难度】★★★【答案】略
【解析】因为GO⊥OH(已知),
所以false(垂直的意义),
因为OH平分∠AOC(已知),
所以false(角平分线的意义).
因为false(邻补角的意义),所以∠GOB+∠HOC=90°(等式性质)
因为∠EDO+∠GOB=90°(已知)所以∠EDO=∠HOC (同角的余角相等)
所以OH∥EF(同位角相等,两直线平行)
【总结】本题综合性较强,主要考查平行线的判定定理及同角的余角相等的综合运用,解题时认真分析,找出角度间的关系.
3422650174625A
B
C
D
E
A
B
C
D
E
【例29】如图,∠ABE=∠E+∠D,试说明AB//CD的理由.
【难度】★★★【答案】略
【解析】因为false(三角形内角和等于180°)
又false(邻补角的意义)
所以∠DCB=∠E+∠D(等式性质)
因为∠ABE=∠E+∠D(已知)
所以∠DCB=∠ABE(等量代换),
所以AB∥CD(内错角相等,两直线平行)
【总结】考查平行线的判定定理及三角形内角和的综合运用,综合性较强,解题时要认真分析.
-101600111760随堂检测
随堂检测
【习题1】27025602508251
7
3
5
6
2
4
1
7
3
5
6
2
4
观察图,下列说法中,正确的是( ).
A.false和false是内错角
B.false和false是同位角
C.false和false是内错角
D.false和false是同旁内角
【难度】★【答案】D
【解析】考查同位角、内错角和同旁内角的概念及判定.
3422650165100A
B
C
D
E
A
B
C
D
E
【习题2】如图,能使AB∥CD的条件是( ).
∠1=∠B B.∠3=∠A
C.∠1+∠2+∠B=180° D.∠1=∠A
【难度】★【答案】C
【解析】同旁内角互补,两直线平行,C选项满足条件.
【总结】考查平行线的判定定理的运用.
【习题3】一学员在广场上练习驾车,两次拐弯后,行驶的方向与原来的方向相同,这两次 拐弯的角度是( )
A.第一次向左拐,第二次向右拐
B.第一次向右拐,第二次向左拐
C.第一次向右拐,第二次向右拐
D.第一次向左拐,第二次向左拐
【难度】★【答案】A
【解析】B向左拐了50°,C、D都朝相反方向开去.
【总结】考查平行线的判定定理在实际问题中的运用.
【习题4】如图,在下列条件中,能判定AB//CD的是( )
A.∠1=∠3 B.∠2=∠3 C.∠1=∠4 D.∠3=∠4
361886533020A
B
C
D
A
B
C
D
【难度】★
【答案】C
【解析】A错误;B能推出AD∥BD;D错误.
【总结】考查平行线的判定定理的运用.
3238500600075【习题5】如图,图中所标号的8个角,是∠1的同位角的是_________;∠3的内错角是 _________;∠7的同旁内角是_________;∠4的同位角是_________;∠6的内错角是 _________;∠2的同旁内角是_________.
【难度】★
【答案】∠2;∠5;∠6、∠8;∠3、∠7;
∠4;∠5.
【解析】考查同位角、内错角、同旁内角的概念.
3455670278765【习题6】如图,已知直线b⊥a,c⊥a.那么直线b与c平行吗?如果平行,请给出证明; 如果不平行,举出反例.
【难度】★★
【答案】平行.
【解析】因为b⊥a,c⊥a(已知),
∴∠1=∠2=90°(垂直的意义),
∴b∥c(同位角相等,两直线平行).
【总结】考查平行线的判定定理及垂直的意义的综合运用.
【习题7】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF
2495550136525A
B
C
D
E
F
1
2
N
M
A
B
C
D
E
F
1
2
N
M
平行吗?为什么?
【难度】★★
【答案】平行.
【解析】因为∠1=35°,∠2=35°(已知),
所以∠1=∠2(等量代换),
因为AC⊥AE,BD⊥BF(已知), 所以false(垂直的意义)
所以∠NBF=∠BAE(等式性质)
所以AE∥BF(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的意义的综合运用.
53079653480435
【习题8】如图,∠1+∠2=180°.AE与FC会平行吗? 说明理由.
【难度】★★【答案】平行.
【解析】因为∠1+∠2=180°(已知),∠2+∠BDC=180°(邻补角的意义)
所以∠1=∠BDC(同角的补角相等)
所以CF∥AE(同位角相等,两直线平行)
【总结】考查平行线的判定定理的运用.
【习题9】根据图完成下列填空(括号内填写定理或公理)
(1)∵∠1=∠4(已知)
∴_________∥_________( )
(2)∵∠ABC +∠_________=180°(已知)
3178810156210A
B
C
D
E
A
B
C
D
E
∴AB∥CD( )
(3)∵∠_________=∠_________(已知)
∴AD∥BC( )
(4)∵∠5=∠_________(已知)
∴AB∥CD( )
【难度】★★
【答案】(1)AB∥CD、内错角相等,两直线平行;
(2)∠BCD、同旁内角互补,两直线平行;
(3)∠2=∠3、内错角相等,两直线平行;
(4)∠ABC、同位角相等,两直线平行.
【解析】考查平行线的判定定理的综合运用.
3365500212090B
C
D
E
F
G
H
B
C
D
E
F
G
H
【习题10】已知DE⊥BC,FG⊥BC,∠DEH=∠GFC,试说明EH∥FC的理由.
【难度】★★
【答案】略.
【解析】因为DE⊥BC,FG⊥BC(已知)
所以∠DEC=∠FGC=90°(垂直的意义)
所以∠GFC+∠FCG=90°(三角形内角和等于180°)
因为∠DEH=∠GFC(已知), 所以∠HEC=∠FCG(等角的余角相等)
所以EH∥FC(内错角相等,两直线平行)
【总结】考查平行线的判定定理的运用.
【习题11】 已知∠EDC+∠B=180°,∠EDC=∠A,试说明AE//BC的理由.
347027538100A
B
C
D
E
A
B
C
D
E
【难度】★★【答案】略
【解析】因为∠EDC+∠B=180°,∠EDC=∠A(已知)
所以∠A+∠B=180°(等量代换)
所以AE∥BC(同旁内角互补,两直线平行)
【总结】考查平行线的判定定理的运用.
【习题12】已知:∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,false.
357505093980A
B
C
D
E
F
A
B
C
D
E
F
试说明DE∥BF的理由.
【难度】★★
【答案】略
【解析】因为BF和DE分别平分∠ABC和∠ADC(已知)
所以false,false(角平分线的意义)
因为∠ABC=∠ADC(已知),所以∠1=∠ABF(等式性质)
因为∠1=∠2(已知), ∴∠2=∠FBA(等量代换)
所以DE∥BF(同位角相等,两直线平行)
3710940123190a
b
c
d
a
b
c
d
【总结】考查平行线的判定定理及角平分线意义的综合运用.
【习题13】已知直线a,b,c被直线d所截,false,试说明a∥c.
【难度】★★【答案】略.
【解析】因为∠1=∠3(已知)
所以a∥b(同位角相等,两直线平行)
因为∠3+∠4=180°(已知),∠3+∠5=180°(邻补角的意义)
所以∠4=∠5(同角的补角相等) 所以b∥c(同位角相等,两直线平行)
所以a∥c(平行的传递性)
【总结】考查平行线的判定定理及平行的传递性的综合运用.
-247650146685课后作业
课后作业
【作业1】下列说法中正确的是( )
A.经过一点,有且只有一条直线与已知直线平行
B.两条直线被第三条直线所截,同位角相等
C.垂直于同一条直线的两条直线互相垂直
D.两条直线被第三条直线所截,内错角相等,则两条直线平行
【难度】★【答案】D
【解析】A这个点必须是直线外的点,错误;B同位角相等的前提是两直线平行,错误;
C垂直于同一条直线的两条直线互相平行,错误;故选D
【总结】考查平面内直线的位置关系.
【作业2】在同一平面内,若a⊥b,c⊥b则a与c的关系是( )
A.平行 B.垂直 C.相交 D.以上都不对
【难度】★【答案】A
【解析】垂直于同一条直线的两条直线互相平行
【总结】考查平面内直线的位置关系.
3740150203200【作业3】如图,∠ADE和∠CED是( )
A.同位角 B.内错角 C.同旁内角 D.互为补角
【难度】★【答案】B
【解析】内错角像字母Z.
【总结】考查内错角的特点及判定.
3100070184150【作业4】如图,属于内错角的是( )
A.∠1和∠2 B.∠2和∠3
C.∠1和∠4 D.∠3和∠4
【难度】★
【答案】D
【解析】内错角像字母Z.
【总结】考查基本角的特点.
【作业5】11430006243320
下列有关垂直相交的说法:
①同一平面内,垂直于同一条直线的两条直线互相平行;
②一条直线如果它与两条平行线中的一条垂直,那么它与另一条也垂直;
③同一平面内, 一条直线不可能与两条相交直线都垂直;
其中说法正确个数有( )
A.3个 B.2个 C.1个 D.0个
【难度】★★【答案】B
【解析】①、③正确,②要在同一平面内才成立,故选C.
【总结】考查平面内直线的位置关系.
【作业6】下列语句:①三条直线只有两个交点,则其中两条直线互相平行;
②如果两条平行线被第三条直线所截,同旁内角相等,那么这两条平行线都与第三条直线垂直;③过一点有且只有一条直线与已知直线平行,其中( )
A.①、②是正确的命题 B.②、③是正确命题
C.①、③是正确命题 D.以上结论皆错
【难度】★★【答案】A
【解析】①正确;②两直线平行,同旁内角互补,此时又相等,所以两个角分别为90°,
即垂直,正确;③这个点必须是直线外的一点,错误,故选A.
【总结】考查平面内直线的位置关系.
【作业7】如图,能与false构成同旁内角的角有( )
falseA.5个 B.4个
C.3个 D.2个
【难度】★★【答案】A
【解析】同旁内角像字母U
【总结】考查基本角的特点及判定.
【作业8】如图,AB⊥BD,CD⊥MN,垂足分别是B、D点,∠FDC=∠EBA.
366712595250(1)判断CD与AB的位置关系;
(2)BE与DF平行吗?为什么?
【难度】★★
【答案】(1)平行 (2)平行
【解析】(1)因为AB⊥BD,CD⊥MN(已知),
所以CD∥AB(垂直于同一条直线的两条直线互相平行);
(2)因为∠CDM=∠ABMfalse(垂直的意义),又∠FDC=∠EBA(已知),
所以∠MDF=∠MBE(等式性质)
所以BE∥DF(同位角相等,两直线平行)
【总结】考查平行线的判定定理及垂直的综合运用.
3670300139700A
B
C
D
E
F
G
A
B
C
D
E
F
G
【作业9】 如图CD⊥AB,EF⊥AB,∠1=∠2,试说明DG//BC的理由.
【难度】★★
【答案】略
【解析】因为CD⊥AB,EF⊥AB(已知),
所以EF∥CD(垂直于同一条直线的两条直线互相平行)
所以∠2=∠DCB(两直线平行,同位角相等)
因为∠2=∠1(已知), 所以∠1=∠DCB(等量代换)
所以DG∥BC(内错角相等,两直线平行)
【总结】考查平行线的判定定理及性质定理的综合运用.
3514725209550【作业10】如图,AB、CD被EF所截,MG平分∠BMN,NH平分∠DNM,
已知∠GMN+∠HNM=90°,试问:AB∥CD吗?请说明理由.
【难度】★★★
【答案】平行.
【解析】因为MG平分∠BMN,NH平分∠DNM(已知)
所以∠BMN=2∠GMN,∠DNM=2∠HNM(角平分线的意义)
因为∠FMG+∠HNM=90°(已知)
所以∠BMN+∠DNM=180°(等式性质)
所以AB∥CD(同旁内角互补,两直线平行)
【总结】考查平行线的判定定理及角平分线的综合运用.
3679190163195A
B
C
D
E
F
A
B
C
D
E
F
【作业11】 如图, ∠B=∠C,∠A=∠D,试说明AE//DF.
【难度】★★★
【答案】略
【解析】因为false,false(三角形内角和等于180°)
又false,false(邻补角的意义)
所以false,false(等式性质)
因为∠B=∠C,∠A=∠D(已知), 所以false(等式性质),
所以AE∥DF(内错角相等,两直线平行)
【总结】考查平行线的判定定理及三角形内角和定理的综合运用,综合性较强,建议老师选择性讲解.
【作业12】如图,已知:∠B+∠D=∠BED.AB与CD平行吗,说明理由.
353377573025A
B
C
D
E
F
A
B
C
D
E
F
【难度】★★★
【答案】略
【解析】过点E作EF∥AB,
则∠B=∠BEF(两直线平行,内错角相等)
因为∠BED =∠BEF+∠FED =∠B+∠D(已知),
所以∠FED=∠D(等式性质)
所以CD∥EF(内错角相等,两直线平行)
所以AB∥CD(平行的传递性)
【总结】考查平行线的判定定理及性质定理的综合运用,教师可选择性的讲解.
同课章节目录
