沪教版(上海)7年级寒假班08-相交线平行线的复习-教师版
文档属性
| 名称 | 沪教版(上海)7年级寒假班08-相交线平行线的复习-教师版 |

|
|
| 格式 | docx | ||
| 文件大小 | 870.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 10:12:36 | ||
图片预览




文档简介
1202690011430000初一数学寒假班(教师版)
教师
日期
学生
课程编号
08
课型
复习课
课题
相交线和平行线复习
教学目标
1.理解三线八角的概念,能够进行简单的角度计算;
2.能够灵活运用平行线的判定定理和性质定理进行证明;
3.能够通过适当的添加辅助线,将复杂的平行线相关的题目证明.
教学重点
理解和掌握平行线的性质定理并进行证明;
2.利用平行线的性质进行角度的计算.
教学安排
版块
时长
1
相交直线
30 min
2
平行直线
40 min
3
综合
20min
4
随堂练习
30 min
63944544450相交线、平行线的复习
相交线、平行线的复习
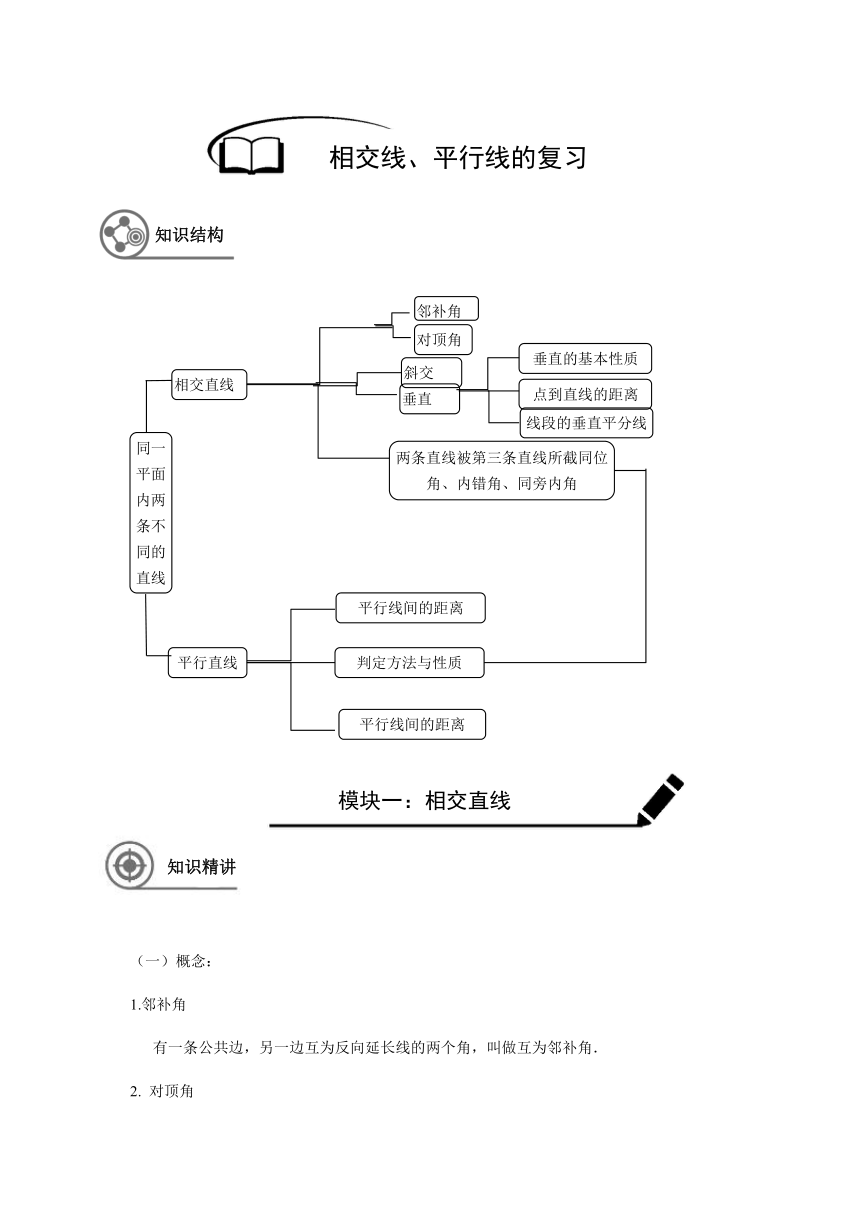
-37147571120 知识结构
知识结构
-2774954840605知识精讲
知识精讲
9309104291965模块一:相交直线
模块一:相交直线
相交直线
两条直线被第三条直线所截同位角、内错角、同旁内角
平行直线
平行线间的距离
平行线间的距离
判定方法与性质
邻补角
垂直
对顶角
同一平面内两条不同的直线
斜交
垂直的基本性质
点到直线的距离
线段的垂直平分线
相交直线
两条直线被第三条直线所截同位角、内错角、同旁内角
平行直线
平行线间的距离
平行线间的距离
判定方法与性质
邻补角
垂直
对顶角
同一平面内两条不同的直线
斜交
垂直的基本性质
点到直线的距离
线段的垂直平分线
(一)概念:
1.邻补角
有一条公共边,另一边互为反向延长线的两个角,叫做互为邻补角.
2. 对顶角
一个角的两边分别为另一个角两边的反向延长线,这样的两个角叫做对顶角.
3. 垂线
两条直线相交所成四个角中,如果有一个角是直角,我们就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
4. 垂线段
过直线外一点,作已知直线的垂线,这点和垂足之间的线段.
5. 点到直线的距离
直线外一点到这条直线的垂线段的长度.
(二)性质:
1. 对顶角的性质:对顶角相等.
2. 邻补角的性质:互为邻补角的两个角和为180°.
3. 垂线的基本性质:
(1)经过一点有且只有一条直线垂直于已知直线;
(2)垂线段最短.
-4000559055例题解析
例题解析
363601055880a
b
l
a
b
l
填空:如右图所示
截线为a,被截线为b、l时:同位角:________________;
内错角:________________;同旁内角:________________;
截线为b,被截线为a、l时:同位角:_________________;
内错角:__________________;同旁内角:_______________.
【难度】★
【答案】false和∠7,∠11和∠6,∠5和∠10,∠8和∠9;
∠8和∠11,∠7和∠10;∠8和∠10,∠7和∠11;∠12和∠3,∠1和∠9,
∠2和∠10,∠4和∠11;∠3和∠10,∠4和∠9;∠4和∠10,∠3和∠9.
【解析】同位角:在直线两旁,被截线的同侧,形如字母F;内错角:在直线两旁,被截线
的两侧,形如字母Z;同旁内角:在直线两旁,被截线的同侧,形如字母U.
【总结】考察内错角、同位角、同旁内角的定义.
3881755422275A
B
C
D
E
F
O
A
B
C
D
E
F
O
如图所示,直线AB和CD相交于点O,OE、OF是过点O的射线,其中构成对顶角的是( )
A.∠AOF和∠DOE B.∠EOF和∠BOE
C.∠COF和∠BOD D.∠BOC和∠AOD
【难度】★
【答案】D
【解析】题目中只有两条直线AB和CD相交于点O,则只有这两条直线才能构成对顶角.
【总结】考察对顶角的定义.
下列说法中,正确的有( )
(1)过两点有且只有一条线段 (2)连结两点的线段叫做两点的距离
(3)两点之间,线段最短 (4)AB=BC,则点B是线段AC的中点
(5)射线比直线短
A.1个 B.2个 C.3个 D.4个
【难度】★【答案】A
【解析】(1)错误,不止一条;(2)错误,两点的距离是连接两点的线段的长度;(3)正确;(4)错误, 点B的位置不能确定,以B为圆心,AB长为半径的圆都满足题意;(5)错误,射线没有端点,所以不能用距离来衡量.综上,(1)、(3)正确.
【总结】考察直线、线段、射线等概念.
如图,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD等于
374650092710A
B
C
D
E
F
O
A
B
C
D
E
F
O
( )
A.40° B.45° C.55° D.65°
【难度】★【答案】A
【解析】∵直线AB、CD相交于点O,
∴false(对顶角相等)
∵EF⊥AB于O(已知), ∴false(垂直的意义)
∴false(等式性质)
【总结】考察对顶角、垂直的定义及运用.
如果∠1与∠2互补,∠1与∠3互余,那么( ).
A.∠2>∠3 B.∠2=∠3
C.∠2<∠3 D.∠2≥∠3
【难度】★★【答案】A
【解析】∵∠1与∠2互补,∠1与∠3互余(已知),
∴false,false(互补及互余的意义)
∴false,false(等式性质) ∴∠2>∠3(不等式的性质的运用)
【总结】考察角度互补、互余的定义.
现在的时间是9点20分,此时钟面上的时针与分针的夹角是( ).
A.false B.155° C.false D.false
【难度】★★【答案】C
【解析】时针的速度是false,则20分钟时针转了false.
而钟面上数字9到数字4(20分钟时,分针指向4)之间的度数为150°
所以此时钟面上的时针与分针的夹角是150°+10°=160°.
【总结】考察时钟问题.注意总结规律:时针的速度是false;分针的速度是false.
3465195351790A
B
C
D
O
E
A
B
C
D
O
E
如图,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是_________.
【难度】★★【答案】30°.
【解析】∵OB平分∠DOE(已知), ∠DOE=60°(已知),
∴false(角平分线的意义)
∵直线AB、CD相交于点O, ∴false(对顶角相等)
【总结】考察角平分线、对顶角的定义及运用.
395986015875a
b
c
d
a
b
c
d
如图,∠1=82°,∠2=98°,∠3=80°,则∠4的度数为_________.
【难度】★★【答案】80°.
【解析】设false的对顶角为∠5, 则∠2=∠5=98°.
∵∠1=82°,∠5=98°(已知)
∴false(等式性质)
∴false(同旁内角互补,两直线平行)
∴false(两直线平行,内错角相等)
【总结】考察对顶角的定义、平行线的判定定理和性质定理的运用.
(1)在下图中画出表示点P到直线a距离的垂线段PM;
38036501397002
1
a
b
P
2
1
a
b
P
(2)过点P画出直线b的平行线c,与直线a交于点N;
(3)如果直线a与b的夹角为35°,求出∠MPN的度数.
【难度】★★
【答案】(1)图上虚线为所求:
(2)图上虚线为所求:
(3)55°.
【解析】略.
【总结】考察垂线段、平行线的画法;平行线的判定和性质的应用.
3943350263525A
B
C
D
E
F
O
A
B
C
D
E
F
O
如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与∠DOF的度数.
【难度】★★
【答案】∠BOF=54°,∠DOF=36°.
【解析】∵CD⊥AB(已知), ∴false(垂直的意义)
∵∠AOE:∠AOD=3:5(已知), ∴false(等式性质)
∵直线AB、EF相交于点O,
∴false(对顶角相等)
∵CD⊥AB(已知), ∴false(垂直的意义)
∴false(等式性质)
【总结】考察对顶角、垂直的定义和应用.
如图所示,已知:BC是从直线AD上出发的一条射线,BE平分∠ABC,
375856557785A
B
C
D
F
E
A
B
C
D
F
E
∠EBF=90°,说明BF平分∠CBD的理由.
【难度】★★
【答案】见解析
【解析】∵BE平分∠ABC(已知),
∴false(角平分线的意义).
∵false(邻补角的意义), ∴false(等式性质)
∵∠EBF=90°(已知), ∴false(等式性质)
∴false(等式性质) ∴false(等量代换)
∴false(等式性质) ∵false(角的和差),
∴false,即BF平分∠CBD(角平分线的意义)
【总结】考察平角、角平分线的定义.注意几何题目中的代数计算.
如图,已知:∠1与∠2互余,DO⊥OC,EO平分∠COD,∠E=110°,
360743519050A
B
C
D
E
O
A
B
C
D
E
O
求∠2的度数.
【难度】★★★【答案】65°
【解析】∵DO⊥OC(已知), ∴false(垂直的意义)
∵false(平角的意义),
∴false(等式性质)
∵∠1与∠2互余(已知), ∴false(互余的意义)
∴false(同角的余角相等), ∴false(内错角相等,两直线平行)
∴false(两直线平行,内错角相等)
∵EO平分∠COD,false(已知)∴false(角平分线的意义)
∴false(等式性质)
【总结】考察互余、垂直、角平分线定义;平行线判定和性质应用.
4362451905模块二:平行线的判定和性质
模块二:平行线的判定和性质
-13525586360知识精讲
知识精讲
1、平行线的基本性质
经过直线外一点,有且只有一条直线与已知直线平行.
推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.平行公理及推论是整个初中平面几何的基石,是其它公理、定理的基础.平行公理及其推论在说明直线平行时,经常用到.
注意:这条性质与垂线的性质很相似,但过任意一点都可以画垂线,而画平行线,只能是过直线外一点才可以.
2、平行线的三种判定方法:
(1)两条直线被第三条直线所截,如果同位角相等,那么两条直线平行,简单地说,同位角相等,两直线平行.
(2)两条直线被第三条直线所截,如果内错角相等,那么两条直线平行,简单地说,内错角相等,两直线平行.
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行,简单地说,同旁内角互补,两直线平行.
-13525564135例题解析
例题解析
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( ).
A.AD∥BC B.∠B=∠C C.∠2+∠B=180° D.AB∥CD
383921031115A
B
C
D
A
B
C
D
【难度】★【答案】B
【解析】∵∠1=∠B(已知),
∴false(同位角相等,两直线平行)
∴false(两直线平行,同旁内角互补)
∵∠2=∠C(已知), ∴false(等量代换),
∴false(同旁内角互补,两直线平行),故选B.
【总结】考察平行线的判定和性质的应用.
如图,所示,false∥false,∠1=120°,∠2=100°,则∠3=( ).
3884930213360falsefalse
falsefalse
1
2
3
falsefalse
falsefalse
1
2
3
A.20° B.40° C.50° D.60°
【难度】★【答案】B
【解析】过中间的折点作平行线,则可得结论:false,
∵∠1=120°,∠2=100°,∴false.
【总结】考察平行线的判定和性质的应用.
如图,已知直线a∥b,c∥d,∠1=115°,那么∠2=_________,∠3=_________.
3884930104140c
d
a
b
c
d
a
b
【难度】★
【答案】115°,115°.
【解析】∵a∥b(已知),
∴false(两直线平行,内错角相等)
∵c∥d(已知),∴false(两直线平行,同位角相等)
【总结】考察平行线的判定和性质的应用.
如图,已知AB∥CD,∠1=100°,∠2=120°,则∠3=________.
【难度】★
【答案】40°
【解析】过折点作平行线
∵false(已作), ∴false(两直线平行,同旁内角互补)
∵false(已知), ∴false(两直线平行,同旁内角互补)
∴false(等式性质)
∵∠1=100°,∠2=120°,(已知) ∴false(等式性质)
∵false(平角的意义) ∴false(等式性质)
【总结】考察平行线的性质和判定的应用.
如图,AB∥CD?,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于( ).
3949700215900F
G
D
C
A
E
B
A
B
C
D
E
F
G
F
G
D
C
A
E
B
A
B
C
D
E
F
G
A.36° B.54° C.72° D.108°
【难度】★★【答案】B
【解析】∵AB∥CD?(已知),
∴false(两直线平行,同旁内角互补)
∵∠EFG=72°(已知), ∴false(等式性质)
∵EG平分∠BEF(已知), ∴false(角平分线的意义)
∵AB∥CD?(已知), ∴false(两直线平行,内错角相等)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
两平行直线被第三条直线所截,同位角的平分线( ).
A.互相重合 B.互相平行 C.互相垂直 D.相交
363220080010【难度】★★
【答案】B
【解析】如图,已知false,直线false分别交直线AB、CD
与E、F,EG平分∠MEB,FH平分∠EFD,则false.
理由如下:
∵false(已知),
∴false(两直线平行,同位角相等)
∵EG平分∠MEB,FH平分∠EFD,(已知)
∴false,false(角平分线的意义)
∴false(等式性质) ∴false(同位角相等,两直线平行)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
如图,若AB∥CD,则∠A、∠E、∠D之间的关系是( )
A.∠A+∠E+∠D=180° B.∠A-∠E+∠D=180°
C.∠A+∠E-∠D=180° D.∠A+∠E+∠D=270°
360997557150【难度】★★【答案】C
【解析】过E作EF∥AB
则false(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB(已知),
∴EF∥CD(平行的传递性)
∴false(两直线平行,内错角相等)
∵false(角的和差)
∴false(等式性质) 即∠A+∠E-∠D=180°.
【总结】考察角平分线的定义;平行线的判定和性质的应用.
如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
3829050114300A
B
C
D
E
M
N
A
B
C
D
E
M
N
【难度】★★【答案】32.5°.
【解析】∵AB∥CD(已知),
∴false(两直线平行,同旁内角互补)
∵∠B=65°(已知), ∴∠ECB=115°(等式性质),
∵CM平分∠BCE(已知),
∴false(角平分线的意义)
∵false(平角的意义)
∴false(等式性质)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,并且∠1+∠2=90°,
417195031750A
B
C
D
E
A
B
C
D
E
说明DA⊥AB的理由.
【难度】★★★
【答案】见解析.
【解析】∵CE平分∠BCD,DE平分∠CDA(已知),
∴false,false(角平分线的意义)
∵∠1+∠2=90°(已知),
∴false(等量代换)∴false(等式性质)
∴false(同旁内角互补,两直线平行)
∴false(两直线平行,同旁内角互补)
∵CB⊥AB(已知), ∴false(垂直的意义)
∴false(等式性质),即DA⊥AB.
【总结】考察角平分线的定义;平行线的判定和性质的应用.
false如图,已知AB∥CD,∠DAB=∠DCB,AE平分∠DAB且交BC于E,CF平分∠DCB且交AD于F.试说明AE∥FC的理由.
【难度】★★★【答案】见解析.
【解析】∵AB∥CD(已知),
∴∠DAB+∠D=180°(两直线平行,同旁内角互补)
∵∠DAB=∠DCB(已知), ∴∠DCB+∠D=180°(等量代换),
∴AD∥BC(同旁内角互补,两直线平行)
∵AE平分∠DAB,CF平分∠DCB(已知)
∴false,false(角平分线的意义)
∵∠DAB=∠DCB(已知), ∴∠DAE=∠FCB,(等式性质)
∵AD∥BC(已知), ∴∠DAE=∠AEB(两直线平行,内错角相等)
∵∠DAE=∠FCB(已知), ∴∠AEB=∠FCB(等量代换),
∴AE∥FC(同位角相等,两直线平行)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
454025210820模块三:辅助线的添加
模块三:辅助线的添加
-11811073660例题解析
例题解析
如图所示,在下列四组条件中,能判定AB∥CD的是( )
367347598425A
B
C
D
A
B
C
D
A.∠1=∠2 B.∠ABD=∠BDC
C.∠3=∠4 D.∠BAD+∠ABC=180°
【难度】★
【答案】B
【解析】A、C、D可以判定出AD∥BC,B答案中是由直线AB和直线CD被直线BD所截
构成的同位角.
【总结】考察平行线的判定定理的用法.
下列说法正确的是( )
A.在同一平面内,两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,b∥c,则a∥c
D.两条直线不相交就平行
【难度】★【答案】C
【解析】A答案错误,两条不相交的直线也可以重合;B答案错误,一条直线的平行线有无
数条;D答案错误,在同一平面内,两条直线不相交就平行.
【总结】考查同一平面内,两直线的位置关系.
已知在同一平面内的三条直线a,b,c,下列命题中错误的是( )
A.如果a∥b,b∥c,那么a∥c B.如果a⊥b,b⊥c,那么a⊥c
如果a⊥b,b⊥c,那么a∥c D.如果a⊥b,a∥c,那么b⊥c
【难度】★★【答案】B
【解析】B答案错误,正确结果为:如果a⊥b,b⊥c,那么a∥c
【总结】考察平行线的传递性、垂直的性质的综合运用.
384810076200A
B
C
D
E
F
A
B
C
D
E
F
如图,AF平分∠BAC,DE平分∠BDF,且∠1=∠2,
试说明:DE∥AF,DF∥AC的理由.
【难度】★★
【答案】见解析
【解析】∵AF平分∠BAC,DE平分∠BDF(已知),
∴false,false(角平分线的意义)
∵∠1=∠2(已知), ∴false(等式性质),
∴DE∥AF(同位角相等,两直线平行)
∴false(两直线平行,内错角相等)
∵false(已证) ∴false(等量代换)
∵∠1=∠2(已知), ∴false(等量代换),
∴DF∥AC(内错角相等,两直线平行)
【总结】考察平行线的判定和性质的应用.
3686175210820A
B
C
D
E
F
G
A
B
C
D
E
F
G
如图所示,AB∥CD,∠BAE=30°,∠DCE=60°,EF、EG三等分∠AEC,问:EF与EG中有没有与AB平行的直线,为什么?
【难度】★★★
【答案】有,EF∥AB,理由见解析.
【解析】∵AB∥CD,∴false
∵EF、EG三等分∠AEC,∴false
∴false,∴EF∥AB(内错角相等,两直线平行)
420751075565A
B
C
D
E
F
A
B
C
D
E
F
【总结】考察平行线的判定和性质的应用.
如图,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C的理由.
【难度】★★★【答案】见解析.
【解析】∵false(邻补角的意义),∠1+∠2=180°(已知),
∴false(同角的补角相等), ∴false(内错角相等,两直线平行),
∴false(两直线平行,内错角相等) ∵∠3=∠B(已知),
∴false(等量代换), ∴false(同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等)
【总结】考察平行线的判定和性质的应用.
4114800299085A
B
C
D
E
F
G
P
A
B
C
D
E
F
G
P
已知DB//FG//EC,∠ABD=60°,∠ACE=40°,AP是∠BAC的平分线.求∠PAG的度数.
【难度】★★★【答案】10°.
【解析】∵DB//FG//EC,∠ABD=60°,∠ACE=40°(已知),
∴false,false
(两直线平行,内错角相等)
∴false(等式性质)
∵AP是∠BAC的平分线(已知)∴false(角平分线的意义)
∴false(等式性质)
【总结】考察平行线的性质及角平分线的意义的综合应用.
3733800360680A
D
C
B
E
F
G
A
D
C
B
E
F
G
如图,长方形ABCD中,E为AB上一点,把△CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,求∠BCE的度数.
【难度】★★★【答案】50°
【解析】∵四边形ABCD是长方形(已知),
∴false,false(长方形的意义)
∴false(两直线平行,内错角相等)
根据折叠的性质可得:false(等式性质)
则false(等式性质)
【总结】考察平行线的性质和翻折性质的综合应用.
-16891054610随堂检测
随堂检测
下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线 B.互相垂直的两条线段一定相交
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短的线段长是3cm,则
点A到直线c的距离是3cm
【难度】★【答案】D
【解析】A错误,过一点有且只有一条直线垂直于已知直线;B错误.因为线段不能无限延
伸,所以互相垂直的两条线段不一定相交;C错误.从直线外一点到这条直线的垂线段
的长度,叫做这点到这条直线的距离.
【总结】考察两条直线相交的性质.
下列语句正确的是( )
A.相等的角是对顶角 B.不是对顶角的角都不相等
C.不相等的角一定不是对顶角 D.有公共点且和为180°的两个角是对顶角
【难度】★【答案】C
【解析】A错误,相等的角也有可能不是对顶角;B错误,不是对顶角的角也有可能相等;
D错误,有一条公共边,另一边互为反向延长线的两个角,叫做互为邻补角.
【总结】考察对顶角、邻补角的定义.
如图点E在AC延长线上,下列条件中能判断AB∥CD的是( )
3882390161925A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=1800
【难度】★【答案】B
【解析】∠1和∠2是由直线AB和直线CD被直线BC所截得到
的内错角,所以选B
【总结】考察平行线的判定方法.
4201160442595A
B
C
D
E
F
A
B
C
D
E
F
如图所示,给出了四个判断①∠1的内错角只有∠3;②∠A的同旁内角只有∠1、∠5;③∠2的内错角只有∠4;④图中的同位角有6对,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【难度】★★
【答案】A
【解析】①正确;
②错误,∠A的同旁内角只有∠1、∠5、false、false;
③错误;∠2的内错角有∠4、false;
④错误;false和false,false和∠5,∠5和∠3,false和false,∠2和false、∠4和false、∠1和false、∠4和false共8对.所以只有①正确.
【总结】考察同位角、内错角、同旁内角的定义.
3041650247650A
B
C
D
E
F
O
A
B
C
D
E
F
O
如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,
∠2:∠1=4:1,求∠AOF的大小.
【难度】★★
【答案】false.
【解析】∵∠2:∠1=4:1,
∴设false,false
∵OE平分∠BOD(已知),
∴false(角平分线的意义)
∵false(邻补角的意义),
∴false,即false(等式性质)∴false(邻补角的意义)
∵OF平分∠COE(已知), ∴false(角平分线的意义)
∵直线AB、CD相交于点O, ∴false(对顶角相等)
∴false(等式性质)
【总结】考察角度计算的方法.
如图所示,
332803516510A
B
C
D
E
A
B
C
D
E
(1)若∠A=∠3,则______∥______;
(2)若∠2=∠E,则______∥______;
(3)若∠A+∠ABE=180°,则______∥______.
【难度】★★
【答案】(1)false;(2)false;(3)false.
【解析】(1)∠A和∠3是由直线AD和直线BE被直线BD所截得到的同位角;
∠E和∠2是由直线DB和直线CE被直线BE所截得到的内错角;
∠A和∠ABE是由直线AD和直线BE被直线AB所截得到的同旁内角.
【总结】考察平行线的判定方法.
361950031750A
B
C
D
E
F
A
B
C
D
E
F
如图,已知AB∥ED,求证:∠B+∠D=∠C.
【难度】★★
【答案】见解析.
【解析】过C作CF∥AB,
∴false(两直线平行,内错角相等)
∵AB∥ED,CF∥AB(已知), ∴CF∥ED(平行的传递性)
∴false(两直线平行,内错角相等)
∵false(角的和差),∴∠B+∠D=∠C(等量代换).
【总结】考察平行线的性质的应用.
已知∠ABE+∠CEB=180°,∠ABF=∠DEG,说明∠F=∠G的理由.
3327400107950【难度】★★
【答案】见解析
【解析】∵∠ABE+∠CEB=180°(已知),
∴false(同旁内角互补,两直线平行)
∴false(两直线平行,内错角相等)
∴false(角的和差)
∵∠ABF=∠DEG(已知) ∴∠FBE=∠BEG(等式性质),
∴BF∥EG(内错角相等,两直线平行), ∴∠F=∠G(两直线平行,内错角相等)
【总结】考察平行线的判定和性质的综合运用.
5362575234315
已知AC、BC分别平分∠QAB、∠ABN,且∠1与∠2互余,试说明PQ//MN.
396684588900A
B
C
P
Q
M
N
A
B
C
P
Q
M
N
【难度】★★【答案】见解析.
【解析】∵AC、BC分别平分∠QAB、∠ABN(已知),
∴false,false(角平分线的意义)
∵∠1与∠2互余(已知), ∴false(互余的意义)
∴false(等量代换)∴false(等式性质)
∴PQ//MN(同旁内角互补,两直线平行).
【总结】考察平行线判定定理及角平分线的应用.
3978910629920已知:如图,把一张长方形纸片的一角沿EF翻折,使顶点A落在false处,再将另一角沿CE翻折过去与使false落在直线false上,CE为折痕,求两条折痕的夹角
∠FEC为多少度?
【难度】★★★
【答案】90°.
【解析】由折叠的性质可得:false,false,
∵falsefalse(平角的意义)
∴falsefalse(等式性质)
即false(角的和差)
【总结】考察折叠的性质综合运用.
-13081076835课后作业
课后作业
下列说法正确的有( )
①一条直线与平行线中的一条直线垂直,则这条直线也垂直于另一条直线;
②邻补角的两条平分线互相垂直;
③平行线的同旁内角的平分线互相垂直;
④同时垂直于第三条直线的两条直线互相垂直.
A.4个 B.3个 C.2个 D.1个
【难度】★【答案】B
【解析】①②③正确,④错误,同时垂直于第三条直线的两条直线平行.
【总结】考察平行线的性质和判定.
396240028575如图,能与∠false构成同旁内角的角有( )
A.3个 B.4个 C.5个 D.6个
【难度】★【答案】C
【解析】同旁内角的定义:两个角都在截线的一侧,且在两条直线之间的一对叫互为同旁内 角.
【总结】考察同旁内角的定义.
如图所示,若已知∠D+∠C=180°,可判定直线______和______平行;
400050082550A
B
E
D
F
C
A
B
E
D
F
C
若∠1=∠2,可以判定直线______和______平行.
【难度】★【答案】AD、BC、AB、CD.
【解析】同旁内角互补,两直线平行;内错角相等,两直线平行.
【总结】考察平行线的判定方法的运用.
如果两个角的两条边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.false B.都是false
C.false或10°,false D.以上答案都不对
【难度】★★【答案】C
【解析】两个角的两条边分别平行,则这两个角相等或者互补.当两角相等时,则这两个角
都等于10°;当两角互补时,两个角为false.
【总结】考察平行线的性质,注意分类讨论.
如下图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC为( )
right10160A.30° B.60°
C.90° D.120°
【难度】★★【答案】B
【解析】∵AD∥BC,∠B=30°,(已知)
∴false(两直线平行,内错角相等)
∵DB平分∠ADE(已知), ∴false(角平分线的意义)
∵AD∥BC(已知),∴false(两直线平行,内错角相等)
【总结】考察平行线的性质和角平分线的定义.
3588385205105A
B
C
P
E
F
H
A
B
C
P
E
F
H
如图,已知∠B=50°,过∠ABC内一点P作PE//AB,PF//BC,PH⊥AB.
求∠FPH的度数.
【难度】★★【答案】40°
【解析】∵PF//BC,∠B=50°,(已知)
∴false(两直线平行,同位角相等)
∵PH⊥AB(已知), ∴false(垂直的意义)
∵false(三角形内角和等于180°)
∴∠FPH=40°(等式性质)
【总结】考察平行线的性质的应用.
372427559055A
B
C
D
E
F
G
A
B
C
D
E
F
G
如图CD⊥AB,EF⊥AB,∠1=∠2,说明DG//BC的理由.
【难度】★★
【答案】见解析.
【解析】∵CD⊥AB,EF⊥AB,(已知)
∴false(垂直于同一条直线的两直线互相平行)
∴false(两直线平行,同位角相等)
∵∠1=∠2(已知), ∴false(等量代换)
∴DG//BC(内错角相等,两直线平行)
【总结】考察平行线的性质和判定的应用.
3895725340360A
B
C
D
A
B
C
D
如图,已知AD∥BC,∠1=∠2,∠A=118°,且BD⊥DC,则∠ABC=_________,∠ADB=_________,∠C=__________.
【难度】★★
【答案】62°;31°;59°.
【解析】∵AD∥BC(已知),
∴false(两直线平行,同旁内角互补)
∵∠A=118°(已知), ∴false(等式性质)
∵∠1=∠2(已知), ∴∠1=∠2=31°(等式性质)
∵AD∥BC(已知), ∴false(两直线平行,内错角相等)
∵BD⊥DC(已知), ∴false(垂直的意义)
∵false(三角形内角和等于180°),∴false(等式性质)
【总结】考察平行线的性质和角平分线的定义.
3387090504825如右图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4,若已知∠1=45°,∠3=65°,求∠2的度数.
【难度】★★★
【答案】55°.
【解析】由题意有:∠6=∠1=45°,∠5=∠3=65°,
∴∠2=(45°+65°)÷2=55°.
【总结】考察三角形内角和为180°.
如图,已知∠1=∠2=∠3,∠GFA=false,∠ACB=false,AQ平分∠FAC,
362521550800A
B
C
D
E
F
G
H
Q
A
B
C
D
E
F
G
H
Q
求∠HAQ的度数.
【难度】★★★
【答案】12°.
【解析】∵∠1=∠2(已知),
∴EF∥AH,(同位角相等,两直线平行)
∴false(两直线平行,内错角相等)
∵∠2=∠3(已知), ∴AH∥BD(同位角相等,两直线平行),
∴false(两直线平行,内错角相等)
∴false(等式性质)
∵AQ平分∠FAC(已知), ∴false(角平分线的意义)
∴false(等式性质)
【总结】考察平行线的性质和判定的应用.
教师
日期
学生
课程编号
08
课型
复习课
课题
相交线和平行线复习
教学目标
1.理解三线八角的概念,能够进行简单的角度计算;
2.能够灵活运用平行线的判定定理和性质定理进行证明;
3.能够通过适当的添加辅助线,将复杂的平行线相关的题目证明.
教学重点
理解和掌握平行线的性质定理并进行证明;
2.利用平行线的性质进行角度的计算.
教学安排
版块
时长
1
相交直线
30 min
2
平行直线
40 min
3
综合
20min
4
随堂练习
30 min
63944544450相交线、平行线的复习
相交线、平行线的复习
-37147571120 知识结构
知识结构
-2774954840605知识精讲
知识精讲
9309104291965模块一:相交直线
模块一:相交直线
相交直线
两条直线被第三条直线所截同位角、内错角、同旁内角
平行直线
平行线间的距离
平行线间的距离
判定方法与性质
邻补角
垂直
对顶角
同一平面内两条不同的直线
斜交
垂直的基本性质
点到直线的距离
线段的垂直平分线
相交直线
两条直线被第三条直线所截同位角、内错角、同旁内角
平行直线
平行线间的距离
平行线间的距离
判定方法与性质
邻补角
垂直
对顶角
同一平面内两条不同的直线
斜交
垂直的基本性质
点到直线的距离
线段的垂直平分线
(一)概念:
1.邻补角
有一条公共边,另一边互为反向延长线的两个角,叫做互为邻补角.
2. 对顶角
一个角的两边分别为另一个角两边的反向延长线,这样的两个角叫做对顶角.
3. 垂线
两条直线相交所成四个角中,如果有一个角是直角,我们就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
4. 垂线段
过直线外一点,作已知直线的垂线,这点和垂足之间的线段.
5. 点到直线的距离
直线外一点到这条直线的垂线段的长度.
(二)性质:
1. 对顶角的性质:对顶角相等.
2. 邻补角的性质:互为邻补角的两个角和为180°.
3. 垂线的基本性质:
(1)经过一点有且只有一条直线垂直于已知直线;
(2)垂线段最短.
-4000559055例题解析
例题解析
363601055880a
b
l
a
b
l
填空:如右图所示
截线为a,被截线为b、l时:同位角:________________;
内错角:________________;同旁内角:________________;
截线为b,被截线为a、l时:同位角:_________________;
内错角:__________________;同旁内角:_______________.
【难度】★
【答案】false和∠7,∠11和∠6,∠5和∠10,∠8和∠9;
∠8和∠11,∠7和∠10;∠8和∠10,∠7和∠11;∠12和∠3,∠1和∠9,
∠2和∠10,∠4和∠11;∠3和∠10,∠4和∠9;∠4和∠10,∠3和∠9.
【解析】同位角:在直线两旁,被截线的同侧,形如字母F;内错角:在直线两旁,被截线
的两侧,形如字母Z;同旁内角:在直线两旁,被截线的同侧,形如字母U.
【总结】考察内错角、同位角、同旁内角的定义.
3881755422275A
B
C
D
E
F
O
A
B
C
D
E
F
O
如图所示,直线AB和CD相交于点O,OE、OF是过点O的射线,其中构成对顶角的是( )
A.∠AOF和∠DOE B.∠EOF和∠BOE
C.∠COF和∠BOD D.∠BOC和∠AOD
【难度】★
【答案】D
【解析】题目中只有两条直线AB和CD相交于点O,则只有这两条直线才能构成对顶角.
【总结】考察对顶角的定义.
下列说法中,正确的有( )
(1)过两点有且只有一条线段 (2)连结两点的线段叫做两点的距离
(3)两点之间,线段最短 (4)AB=BC,则点B是线段AC的中点
(5)射线比直线短
A.1个 B.2个 C.3个 D.4个
【难度】★【答案】A
【解析】(1)错误,不止一条;(2)错误,两点的距离是连接两点的线段的长度;(3)正确;(4)错误, 点B的位置不能确定,以B为圆心,AB长为半径的圆都满足题意;(5)错误,射线没有端点,所以不能用距离来衡量.综上,(1)、(3)正确.
【总结】考察直线、线段、射线等概念.
如图,直线AB、CD相交于点O,EF⊥AB于O,且∠COE=50°,则∠BOD等于
374650092710A
B
C
D
E
F
O
A
B
C
D
E
F
O
( )
A.40° B.45° C.55° D.65°
【难度】★【答案】A
【解析】∵直线AB、CD相交于点O,
∴false(对顶角相等)
∵EF⊥AB于O(已知), ∴false(垂直的意义)
∴false(等式性质)
【总结】考察对顶角、垂直的定义及运用.
如果∠1与∠2互补,∠1与∠3互余,那么( ).
A.∠2>∠3 B.∠2=∠3
C.∠2<∠3 D.∠2≥∠3
【难度】★★【答案】A
【解析】∵∠1与∠2互补,∠1与∠3互余(已知),
∴false,false(互补及互余的意义)
∴false,false(等式性质) ∴∠2>∠3(不等式的性质的运用)
【总结】考察角度互补、互余的定义.
现在的时间是9点20分,此时钟面上的时针与分针的夹角是( ).
A.false B.155° C.false D.false
【难度】★★【答案】C
【解析】时针的速度是false,则20分钟时针转了false.
而钟面上数字9到数字4(20分钟时,分针指向4)之间的度数为150°
所以此时钟面上的时针与分针的夹角是150°+10°=160°.
【总结】考察时钟问题.注意总结规律:时针的速度是false;分针的速度是false.
3465195351790A
B
C
D
O
E
A
B
C
D
O
E
如图,直线AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,则∠AOC的度数是_________.
【难度】★★【答案】30°.
【解析】∵OB平分∠DOE(已知), ∠DOE=60°(已知),
∴false(角平分线的意义)
∵直线AB、CD相交于点O, ∴false(对顶角相等)
【总结】考察角平分线、对顶角的定义及运用.
395986015875a
b
c
d
a
b
c
d
如图,∠1=82°,∠2=98°,∠3=80°,则∠4的度数为_________.
【难度】★★【答案】80°.
【解析】设false的对顶角为∠5, 则∠2=∠5=98°.
∵∠1=82°,∠5=98°(已知)
∴false(等式性质)
∴false(同旁内角互补,两直线平行)
∴false(两直线平行,内错角相等)
【总结】考察对顶角的定义、平行线的判定定理和性质定理的运用.
(1)在下图中画出表示点P到直线a距离的垂线段PM;
38036501397002
1
a
b
P
2
1
a
b
P
(2)过点P画出直线b的平行线c,与直线a交于点N;
(3)如果直线a与b的夹角为35°,求出∠MPN的度数.
【难度】★★
【答案】(1)图上虚线为所求:
(2)图上虚线为所求:
(3)55°.
【解析】略.
【总结】考察垂线段、平行线的画法;平行线的判定和性质的应用.
3943350263525A
B
C
D
E
F
O
A
B
C
D
E
F
O
如图所示,直线AB、CD、EF相交于点O,CD⊥AB,∠AOE:∠AOD=3:5,求∠BOF与∠DOF的度数.
【难度】★★
【答案】∠BOF=54°,∠DOF=36°.
【解析】∵CD⊥AB(已知), ∴false(垂直的意义)
∵∠AOE:∠AOD=3:5(已知), ∴false(等式性质)
∵直线AB、EF相交于点O,
∴false(对顶角相等)
∵CD⊥AB(已知), ∴false(垂直的意义)
∴false(等式性质)
【总结】考察对顶角、垂直的定义和应用.
如图所示,已知:BC是从直线AD上出发的一条射线,BE平分∠ABC,
375856557785A
B
C
D
F
E
A
B
C
D
F
E
∠EBF=90°,说明BF平分∠CBD的理由.
【难度】★★
【答案】见解析
【解析】∵BE平分∠ABC(已知),
∴false(角平分线的意义).
∵false(邻补角的意义), ∴false(等式性质)
∵∠EBF=90°(已知), ∴false(等式性质)
∴false(等式性质) ∴false(等量代换)
∴false(等式性质) ∵false(角的和差),
∴false,即BF平分∠CBD(角平分线的意义)
【总结】考察平角、角平分线的定义.注意几何题目中的代数计算.
如图,已知:∠1与∠2互余,DO⊥OC,EO平分∠COD,∠E=110°,
360743519050A
B
C
D
E
O
A
B
C
D
E
O
求∠2的度数.
【难度】★★★【答案】65°
【解析】∵DO⊥OC(已知), ∴false(垂直的意义)
∵false(平角的意义),
∴false(等式性质)
∵∠1与∠2互余(已知), ∴false(互余的意义)
∴false(同角的余角相等), ∴false(内错角相等,两直线平行)
∴false(两直线平行,内错角相等)
∵EO平分∠COD,false(已知)∴false(角平分线的意义)
∴false(等式性质)
【总结】考察互余、垂直、角平分线定义;平行线判定和性质应用.
4362451905模块二:平行线的判定和性质
模块二:平行线的判定和性质
-13525586360知识精讲
知识精讲
1、平行线的基本性质
经过直线外一点,有且只有一条直线与已知直线平行.
推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.平行公理及推论是整个初中平面几何的基石,是其它公理、定理的基础.平行公理及其推论在说明直线平行时,经常用到.
注意:这条性质与垂线的性质很相似,但过任意一点都可以画垂线,而画平行线,只能是过直线外一点才可以.
2、平行线的三种判定方法:
(1)两条直线被第三条直线所截,如果同位角相等,那么两条直线平行,简单地说,同位角相等,两直线平行.
(2)两条直线被第三条直线所截,如果内错角相等,那么两条直线平行,简单地说,内错角相等,两直线平行.
(3)两条直线被第三条直线所截,如果同旁内角互补,那么两条直线平行,简单地说,同旁内角互补,两直线平行.
-13525564135例题解析
例题解析
如图,已知∠1=∠B,∠2=∠C,则下列结论不成立的是( ).
A.AD∥BC B.∠B=∠C C.∠2+∠B=180° D.AB∥CD
383921031115A
B
C
D
A
B
C
D
【难度】★【答案】B
【解析】∵∠1=∠B(已知),
∴false(同位角相等,两直线平行)
∴false(两直线平行,同旁内角互补)
∵∠2=∠C(已知), ∴false(等量代换),
∴false(同旁内角互补,两直线平行),故选B.
【总结】考察平行线的判定和性质的应用.
如图,所示,false∥false,∠1=120°,∠2=100°,则∠3=( ).
3884930213360falsefalse
falsefalse
1
2
3
falsefalse
falsefalse
1
2
3
A.20° B.40° C.50° D.60°
【难度】★【答案】B
【解析】过中间的折点作平行线,则可得结论:false,
∵∠1=120°,∠2=100°,∴false.
【总结】考察平行线的判定和性质的应用.
如图,已知直线a∥b,c∥d,∠1=115°,那么∠2=_________,∠3=_________.
3884930104140c
d
a
b
c
d
a
b
【难度】★
【答案】115°,115°.
【解析】∵a∥b(已知),
∴false(两直线平行,内错角相等)
∵c∥d(已知),∴false(两直线平行,同位角相等)
【总结】考察平行线的判定和性质的应用.
如图,已知AB∥CD,∠1=100°,∠2=120°,则∠3=________.
【难度】★
【答案】40°
【解析】过折点作平行线
∵false(已作), ∴false(两直线平行,同旁内角互补)
∵false(已知), ∴false(两直线平行,同旁内角互补)
∴false(等式性质)
∵∠1=100°,∠2=120°,(已知) ∴false(等式性质)
∵false(平角的意义) ∴false(等式性质)
【总结】考察平行线的性质和判定的应用.
如图,AB∥CD?,直线EF分别交AB,CD于E,F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,则∠EGF等于( ).
3949700215900F
G
D
C
A
E
B
A
B
C
D
E
F
G
F
G
D
C
A
E
B
A
B
C
D
E
F
G
A.36° B.54° C.72° D.108°
【难度】★★【答案】B
【解析】∵AB∥CD?(已知),
∴false(两直线平行,同旁内角互补)
∵∠EFG=72°(已知), ∴false(等式性质)
∵EG平分∠BEF(已知), ∴false(角平分线的意义)
∵AB∥CD?(已知), ∴false(两直线平行,内错角相等)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
两平行直线被第三条直线所截,同位角的平分线( ).
A.互相重合 B.互相平行 C.互相垂直 D.相交
363220080010【难度】★★
【答案】B
【解析】如图,已知false,直线false分别交直线AB、CD
与E、F,EG平分∠MEB,FH平分∠EFD,则false.
理由如下:
∵false(已知),
∴false(两直线平行,同位角相等)
∵EG平分∠MEB,FH平分∠EFD,(已知)
∴false,false(角平分线的意义)
∴false(等式性质) ∴false(同位角相等,两直线平行)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
如图,若AB∥CD,则∠A、∠E、∠D之间的关系是( )
A.∠A+∠E+∠D=180° B.∠A-∠E+∠D=180°
C.∠A+∠E-∠D=180° D.∠A+∠E+∠D=270°
360997557150【难度】★★【答案】C
【解析】过E作EF∥AB
则false(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB(已知),
∴EF∥CD(平行的传递性)
∴false(两直线平行,内错角相等)
∵false(角的和差)
∴false(等式性质) 即∠A+∠E-∠D=180°.
【总结】考察角平分线的定义;平行线的判定和性质的应用.
如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
3829050114300A
B
C
D
E
M
N
A
B
C
D
E
M
N
【难度】★★【答案】32.5°.
【解析】∵AB∥CD(已知),
∴false(两直线平行,同旁内角互补)
∵∠B=65°(已知), ∴∠ECB=115°(等式性质),
∵CM平分∠BCE(已知),
∴false(角平分线的意义)
∵false(平角的意义)
∴false(等式性质)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
已知:如图,CB⊥AB,CE平分∠BCD,DE平分∠CDA,并且∠1+∠2=90°,
417195031750A
B
C
D
E
A
B
C
D
E
说明DA⊥AB的理由.
【难度】★★★
【答案】见解析.
【解析】∵CE平分∠BCD,DE平分∠CDA(已知),
∴false,false(角平分线的意义)
∵∠1+∠2=90°(已知),
∴false(等量代换)∴false(等式性质)
∴false(同旁内角互补,两直线平行)
∴false(两直线平行,同旁内角互补)
∵CB⊥AB(已知), ∴false(垂直的意义)
∴false(等式性质),即DA⊥AB.
【总结】考察角平分线的定义;平行线的判定和性质的应用.
false如图,已知AB∥CD,∠DAB=∠DCB,AE平分∠DAB且交BC于E,CF平分∠DCB且交AD于F.试说明AE∥FC的理由.
【难度】★★★【答案】见解析.
【解析】∵AB∥CD(已知),
∴∠DAB+∠D=180°(两直线平行,同旁内角互补)
∵∠DAB=∠DCB(已知), ∴∠DCB+∠D=180°(等量代换),
∴AD∥BC(同旁内角互补,两直线平行)
∵AE平分∠DAB,CF平分∠DCB(已知)
∴false,false(角平分线的意义)
∵∠DAB=∠DCB(已知), ∴∠DAE=∠FCB,(等式性质)
∵AD∥BC(已知), ∴∠DAE=∠AEB(两直线平行,内错角相等)
∵∠DAE=∠FCB(已知), ∴∠AEB=∠FCB(等量代换),
∴AE∥FC(同位角相等,两直线平行)
【总结】考察角平分线的定义;平行线的判定和性质的应用.
454025210820模块三:辅助线的添加
模块三:辅助线的添加
-11811073660例题解析
例题解析
如图所示,在下列四组条件中,能判定AB∥CD的是( )
367347598425A
B
C
D
A
B
C
D
A.∠1=∠2 B.∠ABD=∠BDC
C.∠3=∠4 D.∠BAD+∠ABC=180°
【难度】★
【答案】B
【解析】A、C、D可以判定出AD∥BC,B答案中是由直线AB和直线CD被直线BD所截
构成的同位角.
【总结】考察平行线的判定定理的用法.
下列说法正确的是( )
A.在同一平面内,两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.若直线a∥b,b∥c,则a∥c
D.两条直线不相交就平行
【难度】★【答案】C
【解析】A答案错误,两条不相交的直线也可以重合;B答案错误,一条直线的平行线有无
数条;D答案错误,在同一平面内,两条直线不相交就平行.
【总结】考查同一平面内,两直线的位置关系.
已知在同一平面内的三条直线a,b,c,下列命题中错误的是( )
A.如果a∥b,b∥c,那么a∥c B.如果a⊥b,b⊥c,那么a⊥c
如果a⊥b,b⊥c,那么a∥c D.如果a⊥b,a∥c,那么b⊥c
【难度】★★【答案】B
【解析】B答案错误,正确结果为:如果a⊥b,b⊥c,那么a∥c
【总结】考察平行线的传递性、垂直的性质的综合运用.
384810076200A
B
C
D
E
F
A
B
C
D
E
F
如图,AF平分∠BAC,DE平分∠BDF,且∠1=∠2,
试说明:DE∥AF,DF∥AC的理由.
【难度】★★
【答案】见解析
【解析】∵AF平分∠BAC,DE平分∠BDF(已知),
∴false,false(角平分线的意义)
∵∠1=∠2(已知), ∴false(等式性质),
∴DE∥AF(同位角相等,两直线平行)
∴false(两直线平行,内错角相等)
∵false(已证) ∴false(等量代换)
∵∠1=∠2(已知), ∴false(等量代换),
∴DF∥AC(内错角相等,两直线平行)
【总结】考察平行线的判定和性质的应用.
3686175210820A
B
C
D
E
F
G
A
B
C
D
E
F
G
如图所示,AB∥CD,∠BAE=30°,∠DCE=60°,EF、EG三等分∠AEC,问:EF与EG中有没有与AB平行的直线,为什么?
【难度】★★★
【答案】有,EF∥AB,理由见解析.
【解析】∵AB∥CD,∴false
∵EF、EG三等分∠AEC,∴false
∴false,∴EF∥AB(内错角相等,两直线平行)
420751075565A
B
C
D
E
F
A
B
C
D
E
F
【总结】考察平行线的判定和性质的应用.
如图,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C的理由.
【难度】★★★【答案】见解析.
【解析】∵false(邻补角的意义),∠1+∠2=180°(已知),
∴false(同角的补角相等), ∴false(内错角相等,两直线平行),
∴false(两直线平行,内错角相等) ∵∠3=∠B(已知),
∴false(等量代换), ∴false(同位角相等,两直线平行)
∴∠AED=∠C(两直线平行,同位角相等)
【总结】考察平行线的判定和性质的应用.
4114800299085A
B
C
D
E
F
G
P
A
B
C
D
E
F
G
P
已知DB//FG//EC,∠ABD=60°,∠ACE=40°,AP是∠BAC的平分线.求∠PAG的度数.
【难度】★★★【答案】10°.
【解析】∵DB//FG//EC,∠ABD=60°,∠ACE=40°(已知),
∴false,false
(两直线平行,内错角相等)
∴false(等式性质)
∵AP是∠BAC的平分线(已知)∴false(角平分线的意义)
∴false(等式性质)
【总结】考察平行线的性质及角平分线的意义的综合应用.
3733800360680A
D
C
B
E
F
G
A
D
C
B
E
F
G
如图,长方形ABCD中,E为AB上一点,把△CEB沿CE对折,设GE交DC于点F,若∠EFD=80°,求∠BCE的度数.
【难度】★★★【答案】50°
【解析】∵四边形ABCD是长方形(已知),
∴false,false(长方形的意义)
∴false(两直线平行,内错角相等)
根据折叠的性质可得:false(等式性质)
则false(等式性质)
【总结】考察平行线的性质和翻折性质的综合应用.
-16891054610随堂检测
随堂检测
下列说法中正确的是( )
A.有且只有一条直线垂直于已知直线 B.互相垂直的两条线段一定相交
C.从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离
D.直线c外一点A与直线c上各点连接而成的所有线段中,最短的线段长是3cm,则
点A到直线c的距离是3cm
【难度】★【答案】D
【解析】A错误,过一点有且只有一条直线垂直于已知直线;B错误.因为线段不能无限延
伸,所以互相垂直的两条线段不一定相交;C错误.从直线外一点到这条直线的垂线段
的长度,叫做这点到这条直线的距离.
【总结】考察两条直线相交的性质.
下列语句正确的是( )
A.相等的角是对顶角 B.不是对顶角的角都不相等
C.不相等的角一定不是对顶角 D.有公共点且和为180°的两个角是对顶角
【难度】★【答案】C
【解析】A错误,相等的角也有可能不是对顶角;B错误,不是对顶角的角也有可能相等;
D错误,有一条公共边,另一边互为反向延长线的两个角,叫做互为邻补角.
【总结】考察对顶角、邻补角的定义.
如图点E在AC延长线上,下列条件中能判断AB∥CD的是( )
3882390161925A.∠3=∠4 B.∠1=∠2 C.∠D=∠DCE D.∠D+∠ACD=1800
【难度】★【答案】B
【解析】∠1和∠2是由直线AB和直线CD被直线BC所截得到
的内错角,所以选B
【总结】考察平行线的判定方法.
4201160442595A
B
C
D
E
F
A
B
C
D
E
F
如图所示,给出了四个判断①∠1的内错角只有∠3;②∠A的同旁内角只有∠1、∠5;③∠2的内错角只有∠4;④图中的同位角有6对,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【难度】★★
【答案】A
【解析】①正确;
②错误,∠A的同旁内角只有∠1、∠5、false、false;
③错误;∠2的内错角有∠4、false;
④错误;false和false,false和∠5,∠5和∠3,false和false,∠2和false、∠4和false、∠1和false、∠4和false共8对.所以只有①正确.
【总结】考察同位角、内错角、同旁内角的定义.
3041650247650A
B
C
D
E
F
O
A
B
C
D
E
F
O
如图,已知直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE,
∠2:∠1=4:1,求∠AOF的大小.
【难度】★★
【答案】false.
【解析】∵∠2:∠1=4:1,
∴设false,false
∵OE平分∠BOD(已知),
∴false(角平分线的意义)
∵false(邻补角的意义),
∴false,即false(等式性质)∴false(邻补角的意义)
∵OF平分∠COE(已知), ∴false(角平分线的意义)
∵直线AB、CD相交于点O, ∴false(对顶角相等)
∴false(等式性质)
【总结】考察角度计算的方法.
如图所示,
332803516510A
B
C
D
E
A
B
C
D
E
(1)若∠A=∠3,则______∥______;
(2)若∠2=∠E,则______∥______;
(3)若∠A+∠ABE=180°,则______∥______.
【难度】★★
【答案】(1)false;(2)false;(3)false.
【解析】(1)∠A和∠3是由直线AD和直线BE被直线BD所截得到的同位角;
∠E和∠2是由直线DB和直线CE被直线BE所截得到的内错角;
∠A和∠ABE是由直线AD和直线BE被直线AB所截得到的同旁内角.
【总结】考察平行线的判定方法.
361950031750A
B
C
D
E
F
A
B
C
D
E
F
如图,已知AB∥ED,求证:∠B+∠D=∠C.
【难度】★★
【答案】见解析.
【解析】过C作CF∥AB,
∴false(两直线平行,内错角相等)
∵AB∥ED,CF∥AB(已知), ∴CF∥ED(平行的传递性)
∴false(两直线平行,内错角相等)
∵false(角的和差),∴∠B+∠D=∠C(等量代换).
【总结】考察平行线的性质的应用.
已知∠ABE+∠CEB=180°,∠ABF=∠DEG,说明∠F=∠G的理由.
3327400107950【难度】★★
【答案】见解析
【解析】∵∠ABE+∠CEB=180°(已知),
∴false(同旁内角互补,两直线平行)
∴false(两直线平行,内错角相等)
∴false(角的和差)
∵∠ABF=∠DEG(已知) ∴∠FBE=∠BEG(等式性质),
∴BF∥EG(内错角相等,两直线平行), ∴∠F=∠G(两直线平行,内错角相等)
【总结】考察平行线的判定和性质的综合运用.
5362575234315
已知AC、BC分别平分∠QAB、∠ABN,且∠1与∠2互余,试说明PQ//MN.
396684588900A
B
C
P
Q
M
N
A
B
C
P
Q
M
N
【难度】★★【答案】见解析.
【解析】∵AC、BC分别平分∠QAB、∠ABN(已知),
∴false,false(角平分线的意义)
∵∠1与∠2互余(已知), ∴false(互余的意义)
∴false(等量代换)∴false(等式性质)
∴PQ//MN(同旁内角互补,两直线平行).
【总结】考察平行线判定定理及角平分线的应用.
3978910629920已知:如图,把一张长方形纸片的一角沿EF翻折,使顶点A落在false处,再将另一角沿CE翻折过去与使false落在直线false上,CE为折痕,求两条折痕的夹角
∠FEC为多少度?
【难度】★★★
【答案】90°.
【解析】由折叠的性质可得:false,false,
∵falsefalse(平角的意义)
∴falsefalse(等式性质)
即false(角的和差)
【总结】考察折叠的性质综合运用.
-13081076835课后作业
课后作业
下列说法正确的有( )
①一条直线与平行线中的一条直线垂直,则这条直线也垂直于另一条直线;
②邻补角的两条平分线互相垂直;
③平行线的同旁内角的平分线互相垂直;
④同时垂直于第三条直线的两条直线互相垂直.
A.4个 B.3个 C.2个 D.1个
【难度】★【答案】B
【解析】①②③正确,④错误,同时垂直于第三条直线的两条直线平行.
【总结】考察平行线的性质和判定.
396240028575如图,能与∠false构成同旁内角的角有( )
A.3个 B.4个 C.5个 D.6个
【难度】★【答案】C
【解析】同旁内角的定义:两个角都在截线的一侧,且在两条直线之间的一对叫互为同旁内 角.
【总结】考察同旁内角的定义.
如图所示,若已知∠D+∠C=180°,可判定直线______和______平行;
400050082550A
B
E
D
F
C
A
B
E
D
F
C
若∠1=∠2,可以判定直线______和______平行.
【难度】★【答案】AD、BC、AB、CD.
【解析】同旁内角互补,两直线平行;内错角相等,两直线平行.
【总结】考察平行线的判定方法的运用.
如果两个角的两条边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )
A.false B.都是false
C.false或10°,false D.以上答案都不对
【难度】★★【答案】C
【解析】两个角的两条边分别平行,则这两个角相等或者互补.当两角相等时,则这两个角
都等于10°;当两角互补时,两个角为false.
【总结】考察平行线的性质,注意分类讨论.
如下图,已知AD∥BC,∠B=30°,DB平分∠ADE,则∠DEC为( )
right10160A.30° B.60°
C.90° D.120°
【难度】★★【答案】B
【解析】∵AD∥BC,∠B=30°,(已知)
∴false(两直线平行,内错角相等)
∵DB平分∠ADE(已知), ∴false(角平分线的意义)
∵AD∥BC(已知),∴false(两直线平行,内错角相等)
【总结】考察平行线的性质和角平分线的定义.
3588385205105A
B
C
P
E
F
H
A
B
C
P
E
F
H
如图,已知∠B=50°,过∠ABC内一点P作PE//AB,PF//BC,PH⊥AB.
求∠FPH的度数.
【难度】★★【答案】40°
【解析】∵PF//BC,∠B=50°,(已知)
∴false(两直线平行,同位角相等)
∵PH⊥AB(已知), ∴false(垂直的意义)
∵false(三角形内角和等于180°)
∴∠FPH=40°(等式性质)
【总结】考察平行线的性质的应用.
372427559055A
B
C
D
E
F
G
A
B
C
D
E
F
G
如图CD⊥AB,EF⊥AB,∠1=∠2,说明DG//BC的理由.
【难度】★★
【答案】见解析.
【解析】∵CD⊥AB,EF⊥AB,(已知)
∴false(垂直于同一条直线的两直线互相平行)
∴false(两直线平行,同位角相等)
∵∠1=∠2(已知), ∴false(等量代换)
∴DG//BC(内错角相等,两直线平行)
【总结】考察平行线的性质和判定的应用.
3895725340360A
B
C
D
A
B
C
D
如图,已知AD∥BC,∠1=∠2,∠A=118°,且BD⊥DC,则∠ABC=_________,∠ADB=_________,∠C=__________.
【难度】★★
【答案】62°;31°;59°.
【解析】∵AD∥BC(已知),
∴false(两直线平行,同旁内角互补)
∵∠A=118°(已知), ∴false(等式性质)
∵∠1=∠2(已知), ∴∠1=∠2=31°(等式性质)
∵AD∥BC(已知), ∴false(两直线平行,内错角相等)
∵BD⊥DC(已知), ∴false(垂直的意义)
∵false(三角形内角和等于180°),∴false(等式性质)
【总结】考察平行线的性质和角平分线的定义.
3387090504825如右图,光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,这时光线的入射角等于反射角,即∠1=∠6,∠5=∠3,∠2=∠4,若已知∠1=45°,∠3=65°,求∠2的度数.
【难度】★★★
【答案】55°.
【解析】由题意有:∠6=∠1=45°,∠5=∠3=65°,
∴∠2=(45°+65°)÷2=55°.
【总结】考察三角形内角和为180°.
如图,已知∠1=∠2=∠3,∠GFA=false,∠ACB=false,AQ平分∠FAC,
362521550800A
B
C
D
E
F
G
H
Q
A
B
C
D
E
F
G
H
Q
求∠HAQ的度数.
【难度】★★★
【答案】12°.
【解析】∵∠1=∠2(已知),
∴EF∥AH,(同位角相等,两直线平行)
∴false(两直线平行,内错角相等)
∵∠2=∠3(已知), ∴AH∥BD(同位角相等,两直线平行),
∴false(两直线平行,内错角相等)
∴false(等式性质)
∵AQ平分∠FAC(已知), ∴false(角平分线的意义)
∴false(等式性质)
【总结】考察平行线的性质和判定的应用.
同课章节目录
