人教版八年级上册数学学案:14.3.2十字相乘法分解因式
文档属性
| 名称 | 人教版八年级上册数学学案:14.3.2十字相乘法分解因式 |
|
|
| 格式 | zip | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览

文档简介
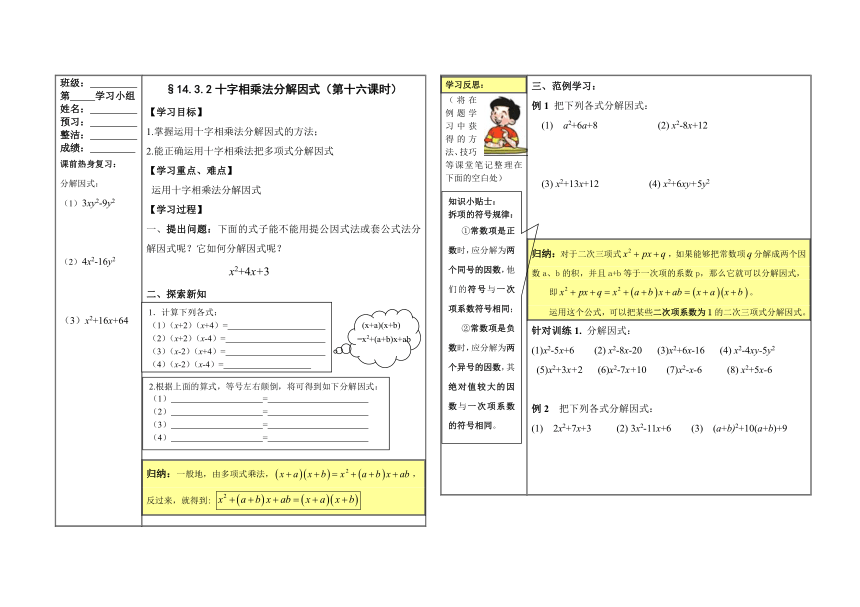
班级:
第
学习小组
姓名:
预习:
整洁:
成绩:
课前热身复习:
分解因式:
(1)3xy2-9y2
(2)4x2-16y2
x2+16x+64
学习反思:
(将在例题学习中获得的方法、技巧等课堂笔记整理在下面的空白处)
§14.3.2十字相乘法分解因式(第十六课时)
【学习目标】
掌握运用十字相乘法分解因式的方法;
能正确运用十字相乘法把多项式分解因式
【学习重点、难点】
运用十字相乘法分解因式
【学习过程】
提出问题:下面的式子能不能用提公因式法或套公式法分解因式呢?它如何分解因式呢?
x2+4x+3
二、探索新知
归纳:一般地,由多项式乘法,,反过来,就得到:
三、范例学习:
例1
把下列各式分解因式:
(1)
a2+6a+8
(2)
x2-8x+12
(3)
x2+13x+12
(4)
x2+6xy+5y2
归纳:对于二次三项式,如果能够把常数项分解成两个因数a、b的积,并且a+b等于一次项的系数p,那么它就可以分解因式,
即。
运用这个公式,可以把某些二次项系数为1的二次三项式分解因式。
针对训练1.
分解因式:
(1)x2-5x+6
(2)
x2-8x-20
(3)x2+6x-16
(4)
x2-4xy-5y2
(5)x2+3x+2
(6)x2-7x+10
(7)x2-x-6
(8)
x2+5x-6
例2
把下列各式分解因式:
(1)
2x2+7x+3
(2)
3x2-11x+6
(3)
(a+b)2+10(a+b)+9
我的课堂笔记:
在此记录下
你的做题过程,对做错的题进行错因分析,改正相信
你会收获很
多。
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
归纳:由上面例子启发我们,应该如何把二次三项式进行因式分解。
我们知道,
反过来,就得到
我们发现,二次项的系数分解成,常数项分解成,并且把,,,排列如下:
这里按斜线交叉相乘,再相加,就得到+,如果它们正好等于的一次项系数,那么就可以分解成:
,其中,位于上图的上一行,,位于下一行。
针对训练2.分解因式:
(1)
x2+7x+6
(2)
2x2-9x+9
(3)
3x2-5x+2
学以致用(自我检测)
用适当的方法分解下列因式
(1)
2x2+7x+5
(2)
2x2-15x+7
(3)
6x2-12x-18
(4)
(a+2b)2+3(a+2b)+2
(5)
(a-b)2-5(a-b)+6
(6)2a2-12a+10
(7)a4-3a2-4
2.思考题:⑴已知:,求的值?
⑵已知:,求的值?
第
学习小组
姓名:
预习:
整洁:
成绩:
课前热身复习:
分解因式:
(1)3xy2-9y2
(2)4x2-16y2
x2+16x+64
学习反思:
(将在例题学习中获得的方法、技巧等课堂笔记整理在下面的空白处)
§14.3.2十字相乘法分解因式(第十六课时)
【学习目标】
掌握运用十字相乘法分解因式的方法;
能正确运用十字相乘法把多项式分解因式
【学习重点、难点】
运用十字相乘法分解因式
【学习过程】
提出问题:下面的式子能不能用提公因式法或套公式法分解因式呢?它如何分解因式呢?
x2+4x+3
二、探索新知
归纳:一般地,由多项式乘法,,反过来,就得到:
三、范例学习:
例1
把下列各式分解因式:
(1)
a2+6a+8
(2)
x2-8x+12
(3)
x2+13x+12
(4)
x2+6xy+5y2
归纳:对于二次三项式,如果能够把常数项分解成两个因数a、b的积,并且a+b等于一次项的系数p,那么它就可以分解因式,
即。
运用这个公式,可以把某些二次项系数为1的二次三项式分解因式。
针对训练1.
分解因式:
(1)x2-5x+6
(2)
x2-8x-20
(3)x2+6x-16
(4)
x2-4xy-5y2
(5)x2+3x+2
(6)x2-7x+10
(7)x2-x-6
(8)
x2+5x-6
例2
把下列各式分解因式:
(1)
2x2+7x+3
(2)
3x2-11x+6
(3)
(a+b)2+10(a+b)+9
我的课堂笔记:
在此记录下
你的做题过程,对做错的题进行错因分析,改正相信
你会收获很
多。
本节反思
1.本节课你有哪些收获?(知识上,思想方法上)
2.课前你的疑难解决了吗?有没有新的问题?
归纳:由上面例子启发我们,应该如何把二次三项式进行因式分解。
我们知道,
反过来,就得到
我们发现,二次项的系数分解成,常数项分解成,并且把,,,排列如下:
这里按斜线交叉相乘,再相加,就得到+,如果它们正好等于的一次项系数,那么就可以分解成:
,其中,位于上图的上一行,,位于下一行。
针对训练2.分解因式:
(1)
x2+7x+6
(2)
2x2-9x+9
(3)
3x2-5x+2
学以致用(自我检测)
用适当的方法分解下列因式
(1)
2x2+7x+5
(2)
2x2-15x+7
(3)
6x2-12x-18
(4)
(a+2b)2+3(a+2b)+2
(5)
(a-b)2-5(a-b)+6
(6)2a2-12a+10
(7)a4-3a2-4
2.思考题:⑴已知:,求的值?
⑵已知:,求的值?
