六年级数学上册课件-3.1 倒数的认识人教版(共76张PPT)
文档属性
| 名称 | 六年级数学上册课件-3.1 倒数的认识人教版(共76张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 06:45:10 | ||
图片预览










文档简介
(共76张PPT)
倒数的认识
知识回顾
8
3
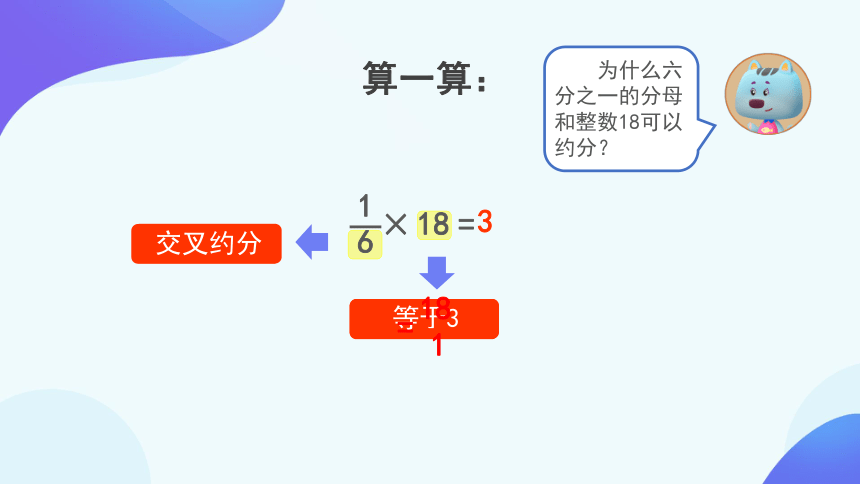
算一算:
=
7
15
15
7
×
=
3
8
×
=
6
1
×
18
=
10
1
×
10
=
12
1
×
12
=
7
6
6
1
×
1
=
9
4
×
0
1
3
=
2
3
3
4
×
=
3
5
×
0.6
算一算:
=
6
1
×
18
3
倍数关系
6与6约分
除以6
等于3
为什么六分之一的分母和整数18可以约分?
交叉约分
1
18
=
8
3
算一算:
=
7
15
15
7
×
1
=
3
8
×
1
=
6
1
×
3
18
=
10
1
×
1
10
=
2
3
3
4
×
2
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
9
4
×
0
0
=
3
5
×
1
0.6
算一算:
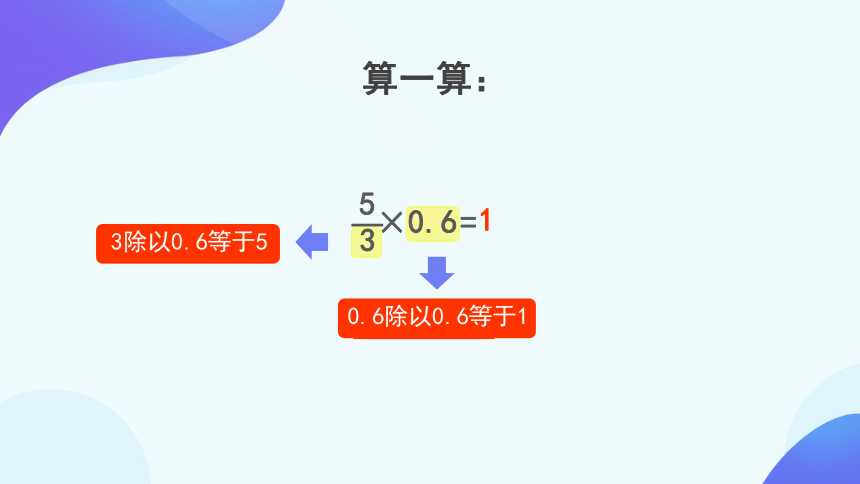
倍数关系
3除以0.6等于5
除以0.6
0.6除以0.6等于1
=
3
5
×
1
0.6
算一算:
交叉约分
有没有同学和他的算法不一样?
=
3
5
×
1
0.6
5
3
8
3
算一算:
=
7
15
15
7
×
1
=
3
8
×
1
=
6
1
×
3
18
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
9
4
×
0
0
=
2
3
3
4
×
2
=
3
5
×
1
0.6
你会怎么分类?
你为什么这样分呢?
乘积是1
8
3
算一算:
=
7
15
15
7
×
1
=
3
8
×
1
=
6
1
×
3
18
=
10
1
×
1
10
=
2
3
3
4
×
2
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
9
4
×
0
0
=
3
5
×
1
0.6
在数学里面乘积是1的两个数
互为倒数
倒数的认识
乘积是1的两个数互为倒数。
倒数的认识
乘积是1的两个数互为倒数。
倒数的认识
你怎样理解倒数的定义?
只能是1
它们相乘的积只能是什么?
乘积是1的两个数互为倒数。
倒数的认识
不能是三个或三个以上的数,互为倒数
倒数是用来描述两个数之间的关系的
乘积是1的两个数互为倒数。
乘积是1的两个数互为倒数。
倒数的认识
互相
互为倒数的互为,是什么意思?
倒数的认识
互相
互为倒数的互为,是什么意思?
两个数都是对方的倒数
我们可以怎么理解互为倒数?
乘积是1的两个数互为倒数。
=
8
3
×
1
倒数的认识
3
8
8
3
3
8
和
互为倒数
我们还可以怎样理解?
倒数的认识
我们还可以怎样理解?
8
3
3
8
和
互为倒数
8
3
3
8
是
的倒数
3
8
8
3
是
的倒数
你真棒!
这位同学不仅通过举例说明了他对互为倒数的理解,更难能可贵的是,他能够通过知识的迁移,理解新的内容。
倒数用来表示的是两个数之间相互依存的一种关系。
我们在描述两个数互为倒数关系的时候,一定要说清楚谁和谁互为倒数,或者要讲清楚谁是谁的倒数。
8
3
课堂活动
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
你能描述一下它们的关系吗?
8
3
课堂活动
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
你能描述一下它们的关系吗?
10
10
1
和
互为倒数
是
的倒数
是
的倒数
课堂活动
10
10
1
10
1
10
8
3
课堂活动
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
你能描述一下它们的关系吗?
0.6
3
5
和
互为倒数
是
的倒数
是
的倒数
课堂活动
0.6
3
5
3
5
0.6
下面哪两个数互为倒数?用线连一连。
6
7
2
0.4
10
99
59
2
7
59
99
0.1
6
1
2.5
乘积等于1
只要两个数的乘积是1,它们就是互为倒数的关系
小红和小亮谁说得对?
小红
小亮
因为
,所以
的倒数是0.75。
分数的倒数不可能是一个小数。
=1
0.75
3
4
×
3
4
分数的倒数不可能是一个小数。
小红和小亮谁说得对?
小红
小亮
因为
,所以
的倒数是0.75。
分数的倒数不可能是一个小数。
3
4
=1
0.75
4
3
×
=1
0.75
3
4
×
√
乘积等于1
互为倒数
只要两个数的乘积是1就互为倒数。这两个数可以是分数,也可以是整数或什么数?
小数。
8
3
例题讲解
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
分数
出现整数
出现小数
同学们,你们能举出两个数互为倒数的例子吗?
10
9
举例
=
4
5
5
4
×
1
=
9
10
×
1
=
6
5
5
6
×
1
谁来说说你举的例子?
互为倒数
互为倒数
10
9
举例
=
4
5
5
4
×
1
=
9
10
×
1
=
6
5
5
6
×
1
分数乘分数,为什么容易约分?
交叉约分
分子分母交换位置
它们有一个特点,是什么?
想一想:是不是所有互为倒数的两个数都具有这一特点?
8
3
想一想:是不是所有互为倒数的两个数都具有这一特点?
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
=
3
5
×
1
5
3
3
5
和
互为倒数
想一想:是不是所有互为倒数的两个数都具有这一特点?
0.6
8
3
想一想:是不是所有互为倒数的两个数都具有这一特点?
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
=
12
1
×
1
1
12
12
1
和
分子分母交换位置
想一想:是不是所有互为倒数的两个数都具有这一特点?
12
=
10
1
×
1
1
10
10
1
和
分子分母交换位置
想一想:是不是所有互为倒数的两个数都具有这一特点?
10
=
3
5
×
1
5
3
3
5
和
互为倒数
想一想:是不是所有互为倒数的两个数都具有这一特点?
0.6
分子分母交换位置
=
×
1
6
7
7
6
和
分子分母交换位置
想一想:是不是所有互为倒数的两个数都具有这一特点?
6
1
1
7
6
8
3
想一想:是不是所有互为倒数的两个数都具有这一特点?
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
转化分数
分子分母交换位置
互为倒数
1
3
1
0.8
35
11
4
写出下面各数的倒数。
9
16
11
4
写出下面各数的倒数。
4
11
=
互为倒数
×
不是大小相同的数
不相等
=
9
16
×
1
写出下面各数的倒数。
16
9
9
16
它的倒数是
16
9
1
35
写出下面各数的倒数。
35
1
它的倒数是
35
1
35
1
35
35=
分子、分母
交换位置
5
4
写出下面各数的倒数。
4
5
它的倒数是
4
5
0.8
5
4
0.8=
分子、分母
交换位置
写出下面各数的倒数。
它的倒数是
分子、分母
交换位置
1
3
1
3
4
=
1
3
1
3
4
4
3
4
3
说一说:怎样求一个数的倒数?
1
3
1
0.8
35
11
4
怎样求一个数的倒数?
9
16
分子分母交换位置
化成分数
分子分母交换位置
你真棒!
1
3
1
0.8
35
11
4
怎样求一个数的倒数?
9
16
化成假分数
分子分母交换位置
1
3
1
0.8
35
11
4
怎样求一个数的倒数?
9
16
分子分母交换位置
化成分数
分子分母交换位置
你真棒!
同学们不仅对倒数有了一定的认识,也能够准确的求出一个数的倒数。
下面数字的倒数是多少?
1
0
1的倒数是多少?
下面数字的倒数是多少?
1
1
1
=
几乘1会等于1?
1只有乘1会等于1
乘积是1的两个数互为倒数。
倒数的定义是什么?
1只有和谁相乘,乘积才会是1。
1。
所以1的倒数是多少?
1。
下面数字的倒数是多少?
1
0
0有倒数吗?
下面数字的倒数是多少?
0
0没有倒数
0乘任何数都等于0
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
下面的说法对不对?为什么?
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
两个数互为倒数
缺少和它互为倒数的数
×
倒数是几个数之间相互的关系?
两个数。
谁是谁的什么?
谁是谁的倒数。
下面的说法对不对?为什么?
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
×
=1,所以
和
互为倒数。
5
9
9
5
9
5
5
9
×
=1,所以
是
的倒数。
5
9
9
5
9
5
5
9
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
×
下面的说法对不对?为什么?
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
乘积是1的两个数互为倒数
应该使用乘法
×
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
×
×
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
×
×
×
下面的说法对不对?为什么?
(5)一个数的倒数一定比这个数小。
1的倒数就是1,它的倒数等于自己。
11
4
4
11
相等
<
一个数的倒数也有可能比它大。
×
—
6
5
×(
)=(
)×4=(
)×0.125=1。
—
5
6
—
1
4
下面的(
)里可以填几?
8
等于1
等于1
等于1
—
6
5
×(
)=(
)×4=(
)×0.125=1。
—
5
6
—
1
4
下面的(
)里可以填几?
8
互为倒数
互为倒数
怎样才会等于1?
倒数
互为倒数
先计算出每组算式的结果,再在○里填上“>”“<”或“=”。
—
1
8
1÷8=(
)
1×
=(
)
1÷8
○
1×
—
1
8
—
1
2
6÷2=(
)
6×
=(
)
6÷2
○
6×
—
1
2
—
1
4
9÷4=(
)
9×
=(
)
9÷4
○
9×
—
1
4
—
1
8
—
1
8
=
—
9
4
—
9
4
=
=
3
3
每一组算式的第1个数都一样
先计算出每组算式的结果,再在○里填上“>”“<”或“=”。
—
1
8
1÷8=(
)
1×
=(
)
1÷8
○
1×
—
1
8
—
1
2
6÷2=(
)
6×
=(
)
6÷2
○
6×
—
1
2
—
1
4
9÷4=(
)
9×
=(
)
9÷4
○
9×
—
1
4
—
1
8
—
1
8
=
—
9
4
—
9
4
=
=
3
3
每一组算式的第2个数都互为倒数
互为倒数
先计算出每组算式的结果,再在○里填上“>”“<”或“=”。
—
1
8
1÷8=(
)
1×
=(
)
1÷8
○
1×
—
1
8
—
1
2
6÷2=(
)
6×
=(
)
6÷2
○
6×
—
1
2
—
1
4
9÷4=(
)
9×
=(
)
9÷4
○
9×
—
1
4
—
1
8
—
1
8
=
—
9
4
—
9
4
=
=
3
3
得数一样
相等
同学们发现了这么多的特征,我们可以得到一个什么结论?
知识小结
一个数除以另一个数,等于这个数乘另一个数的倒数。
一个数除以另一个数,相当于乘这个数的倒数。
同学们,你们的发现十分有价值,这些发现将帮助我们继续更好地学习之后的分数除法课程。
是不是所有的数除以一个数,就是乘它的倒数?这个问题,我们留到下一节课再来研究。
再见!
倒数的认识
知识回顾
8
3
算一算:
=
7
15
15
7
×
=
3
8
×
=
6
1
×
18
=
10
1
×
10
=
12
1
×
12
=
7
6
6
1
×
1
=
9
4
×
0
1
3
=
2
3
3
4
×
=
3
5
×
0.6
算一算:
=
6
1
×
18
3
倍数关系
6与6约分
除以6
等于3
为什么六分之一的分母和整数18可以约分?
交叉约分
1
18
=
8
3
算一算:
=
7
15
15
7
×
1
=
3
8
×
1
=
6
1
×
3
18
=
10
1
×
1
10
=
2
3
3
4
×
2
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
9
4
×
0
0
=
3
5
×
1
0.6
算一算:
倍数关系
3除以0.6等于5
除以0.6
0.6除以0.6等于1
=
3
5
×
1
0.6
算一算:
交叉约分
有没有同学和他的算法不一样?
=
3
5
×
1
0.6
5
3
8
3
算一算:
=
7
15
15
7
×
1
=
3
8
×
1
=
6
1
×
3
18
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
9
4
×
0
0
=
2
3
3
4
×
2
=
3
5
×
1
0.6
你会怎么分类?
你为什么这样分呢?
乘积是1
8
3
算一算:
=
7
15
15
7
×
1
=
3
8
×
1
=
6
1
×
3
18
=
10
1
×
1
10
=
2
3
3
4
×
2
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
9
4
×
0
0
=
3
5
×
1
0.6
在数学里面乘积是1的两个数
互为倒数
倒数的认识
乘积是1的两个数互为倒数。
倒数的认识
乘积是1的两个数互为倒数。
倒数的认识
你怎样理解倒数的定义?
只能是1
它们相乘的积只能是什么?
乘积是1的两个数互为倒数。
倒数的认识
不能是三个或三个以上的数,互为倒数
倒数是用来描述两个数之间的关系的
乘积是1的两个数互为倒数。
乘积是1的两个数互为倒数。
倒数的认识
互相
互为倒数的互为,是什么意思?
倒数的认识
互相
互为倒数的互为,是什么意思?
两个数都是对方的倒数
我们可以怎么理解互为倒数?
乘积是1的两个数互为倒数。
=
8
3
×
1
倒数的认识
3
8
8
3
3
8
和
互为倒数
我们还可以怎样理解?
倒数的认识
我们还可以怎样理解?
8
3
3
8
和
互为倒数
8
3
3
8
是
的倒数
3
8
8
3
是
的倒数
你真棒!
这位同学不仅通过举例说明了他对互为倒数的理解,更难能可贵的是,他能够通过知识的迁移,理解新的内容。
倒数用来表示的是两个数之间相互依存的一种关系。
我们在描述两个数互为倒数关系的时候,一定要说清楚谁和谁互为倒数,或者要讲清楚谁是谁的倒数。
8
3
课堂活动
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
你能描述一下它们的关系吗?
8
3
课堂活动
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
你能描述一下它们的关系吗?
10
10
1
和
互为倒数
是
的倒数
是
的倒数
课堂活动
10
10
1
10
1
10
8
3
课堂活动
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
你能描述一下它们的关系吗?
0.6
3
5
和
互为倒数
是
的倒数
是
的倒数
课堂活动
0.6
3
5
3
5
0.6
下面哪两个数互为倒数?用线连一连。
6
7
2
0.4
10
99
59
2
7
59
99
0.1
6
1
2.5
乘积等于1
只要两个数的乘积是1,它们就是互为倒数的关系
小红和小亮谁说得对?
小红
小亮
因为
,所以
的倒数是0.75。
分数的倒数不可能是一个小数。
=1
0.75
3
4
×
3
4
分数的倒数不可能是一个小数。
小红和小亮谁说得对?
小红
小亮
因为
,所以
的倒数是0.75。
分数的倒数不可能是一个小数。
3
4
=1
0.75
4
3
×
=1
0.75
3
4
×
√
乘积等于1
互为倒数
只要两个数的乘积是1就互为倒数。这两个数可以是分数,也可以是整数或什么数?
小数。
8
3
例题讲解
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
分数
出现整数
出现小数
同学们,你们能举出两个数互为倒数的例子吗?
10
9
举例
=
4
5
5
4
×
1
=
9
10
×
1
=
6
5
5
6
×
1
谁来说说你举的例子?
互为倒数
互为倒数
10
9
举例
=
4
5
5
4
×
1
=
9
10
×
1
=
6
5
5
6
×
1
分数乘分数,为什么容易约分?
交叉约分
分子分母交换位置
它们有一个特点,是什么?
想一想:是不是所有互为倒数的两个数都具有这一特点?
8
3
想一想:是不是所有互为倒数的两个数都具有这一特点?
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
=
3
5
×
1
5
3
3
5
和
互为倒数
想一想:是不是所有互为倒数的两个数都具有这一特点?
0.6
8
3
想一想:是不是所有互为倒数的两个数都具有这一特点?
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
=
12
1
×
1
1
12
12
1
和
分子分母交换位置
想一想:是不是所有互为倒数的两个数都具有这一特点?
12
=
10
1
×
1
1
10
10
1
和
分子分母交换位置
想一想:是不是所有互为倒数的两个数都具有这一特点?
10
=
3
5
×
1
5
3
3
5
和
互为倒数
想一想:是不是所有互为倒数的两个数都具有这一特点?
0.6
分子分母交换位置
=
×
1
6
7
7
6
和
分子分母交换位置
想一想:是不是所有互为倒数的两个数都具有这一特点?
6
1
1
7
6
8
3
想一想:是不是所有互为倒数的两个数都具有这一特点?
=
7
15
15
7
×
1
=
3
8
×
1
=
10
1
×
1
10
=
12
1
×
1
12
=
7
6
6
1
×
1
1
=
3
5
×
1
0.6
转化分数
分子分母交换位置
互为倒数
1
3
1
0.8
35
11
4
写出下面各数的倒数。
9
16
11
4
写出下面各数的倒数。
4
11
=
互为倒数
×
不是大小相同的数
不相等
=
9
16
×
1
写出下面各数的倒数。
16
9
9
16
它的倒数是
16
9
1
35
写出下面各数的倒数。
35
1
它的倒数是
35
1
35
1
35
35=
分子、分母
交换位置
5
4
写出下面各数的倒数。
4
5
它的倒数是
4
5
0.8
5
4
0.8=
分子、分母
交换位置
写出下面各数的倒数。
它的倒数是
分子、分母
交换位置
1
3
1
3
4
=
1
3
1
3
4
4
3
4
3
说一说:怎样求一个数的倒数?
1
3
1
0.8
35
11
4
怎样求一个数的倒数?
9
16
分子分母交换位置
化成分数
分子分母交换位置
你真棒!
1
3
1
0.8
35
11
4
怎样求一个数的倒数?
9
16
化成假分数
分子分母交换位置
1
3
1
0.8
35
11
4
怎样求一个数的倒数?
9
16
分子分母交换位置
化成分数
分子分母交换位置
你真棒!
同学们不仅对倒数有了一定的认识,也能够准确的求出一个数的倒数。
下面数字的倒数是多少?
1
0
1的倒数是多少?
下面数字的倒数是多少?
1
1
1
=
几乘1会等于1?
1只有乘1会等于1
乘积是1的两个数互为倒数。
倒数的定义是什么?
1只有和谁相乘,乘积才会是1。
1。
所以1的倒数是多少?
1。
下面数字的倒数是多少?
1
0
0有倒数吗?
下面数字的倒数是多少?
0
0没有倒数
0乘任何数都等于0
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
下面的说法对不对?为什么?
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
两个数互为倒数
缺少和它互为倒数的数
×
倒数是几个数之间相互的关系?
两个数。
谁是谁的什么?
谁是谁的倒数。
下面的说法对不对?为什么?
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
×
=1,所以
和
互为倒数。
5
9
9
5
9
5
5
9
×
=1,所以
是
的倒数。
5
9
9
5
9
5
5
9
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
×
下面的说法对不对?为什么?
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
乘积是1的两个数互为倒数
应该使用乘法
×
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
×
×
下面的说法对不对?为什么?
(1)
与
的乘积为1,所以
和
互为倒数。
12
7
12
7
7
12
12
7
(4)
×
×
=1,所以
、
、
互为倒数。
1
2
4
3
3
2
1
2
4
3
3
2
(5)一个数的倒数一定比这个数小。
(3)因为
+
=1,所以
是
的倒数。
1
4
3
4
1
4
3
4
(2)
×
=1,所以
是倒数。
5
9
9
5
5
9
√
×
×
×
×
下面的说法对不对?为什么?
(5)一个数的倒数一定比这个数小。
1的倒数就是1,它的倒数等于自己。
11
4
4
11
相等
<
一个数的倒数也有可能比它大。
×
—
6
5
×(
)=(
)×4=(
)×0.125=1。
—
5
6
—
1
4
下面的(
)里可以填几?
8
等于1
等于1
等于1
—
6
5
×(
)=(
)×4=(
)×0.125=1。
—
5
6
—
1
4
下面的(
)里可以填几?
8
互为倒数
互为倒数
怎样才会等于1?
倒数
互为倒数
先计算出每组算式的结果,再在○里填上“>”“<”或“=”。
—
1
8
1÷8=(
)
1×
=(
)
1÷8
○
1×
—
1
8
—
1
2
6÷2=(
)
6×
=(
)
6÷2
○
6×
—
1
2
—
1
4
9÷4=(
)
9×
=(
)
9÷4
○
9×
—
1
4
—
1
8
—
1
8
=
—
9
4
—
9
4
=
=
3
3
每一组算式的第1个数都一样
先计算出每组算式的结果,再在○里填上“>”“<”或“=”。
—
1
8
1÷8=(
)
1×
=(
)
1÷8
○
1×
—
1
8
—
1
2
6÷2=(
)
6×
=(
)
6÷2
○
6×
—
1
2
—
1
4
9÷4=(
)
9×
=(
)
9÷4
○
9×
—
1
4
—
1
8
—
1
8
=
—
9
4
—
9
4
=
=
3
3
每一组算式的第2个数都互为倒数
互为倒数
先计算出每组算式的结果,再在○里填上“>”“<”或“=”。
—
1
8
1÷8=(
)
1×
=(
)
1÷8
○
1×
—
1
8
—
1
2
6÷2=(
)
6×
=(
)
6÷2
○
6×
—
1
2
—
1
4
9÷4=(
)
9×
=(
)
9÷4
○
9×
—
1
4
—
1
8
—
1
8
=
—
9
4
—
9
4
=
=
3
3
得数一样
相等
同学们发现了这么多的特征,我们可以得到一个什么结论?
知识小结
一个数除以另一个数,等于这个数乘另一个数的倒数。
一个数除以另一个数,相当于乘这个数的倒数。
同学们,你们的发现十分有价值,这些发现将帮助我们继续更好地学习之后的分数除法课程。
是不是所有的数除以一个数,就是乘它的倒数?这个问题,我们留到下一节课再来研究。
再见!
