2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第13章三角形中的边角关系、命题与证明(Word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第13章三角形中的边角关系、命题与证明(Word版含解析) | 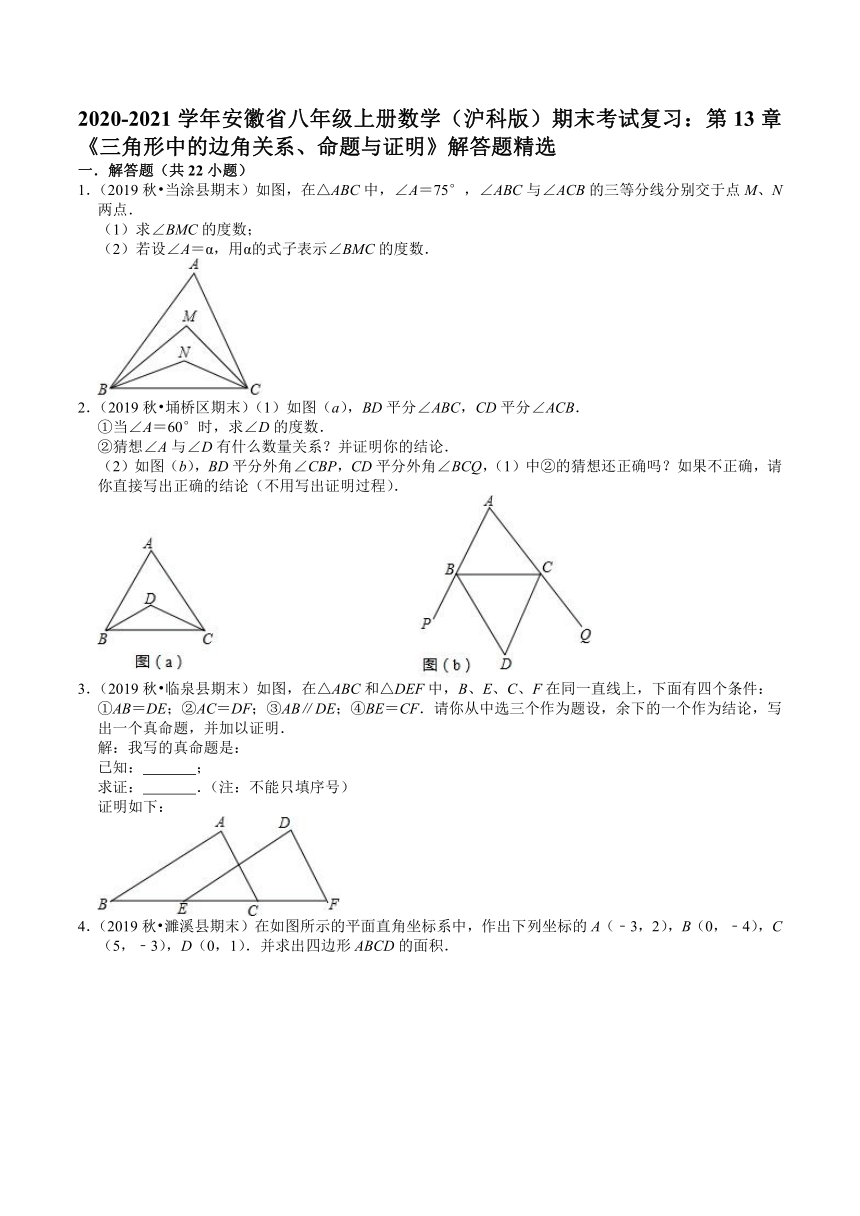 | |
| 格式 | docx | ||
| 文件大小 | 159.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 14:31:20 | ||
图片预览



文档简介
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第13章《三角形中的边角关系、命题与证明》解答题精选
一.解答题(共22小题)
1.(2019秋?当涂县期末)如图,在△ABC中,∠A=75°,∠ABC与∠ACB的三等分线分别交于点M、N两点.
(1)求∠BMC的度数;
(2)若设∠A=α,用α的式子表示∠BMC的度数.
2.(2019秋?埇桥区期末)(1)如图(a),BD平分∠ABC,CD平分∠ACB.
①当∠A=60°时,求∠D的度数.
②猜想∠A与∠D有什么数量关系?并证明你的结论.
(2)如图(b),BD平分外角∠CBP,CD平分外角∠BCQ,(1)中②的猜想还正确吗?如果不正确,请你直接写出正确的结论(不用写出证明过程).
3.(2019秋?临泉县期末)如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件:
①AB=DE;②AC=DF;③AB∥DE;④BE=CF.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知:
;
求证:
.(注:不能只填序号)
证明如下:
4.(2019秋?濉溪县期末)在如图所示的平面直角坐标系中,作出下列坐标的A(﹣3,2),B(0,﹣4),C(5,﹣3),D(0,1).并求出四边形ABCD的面积.
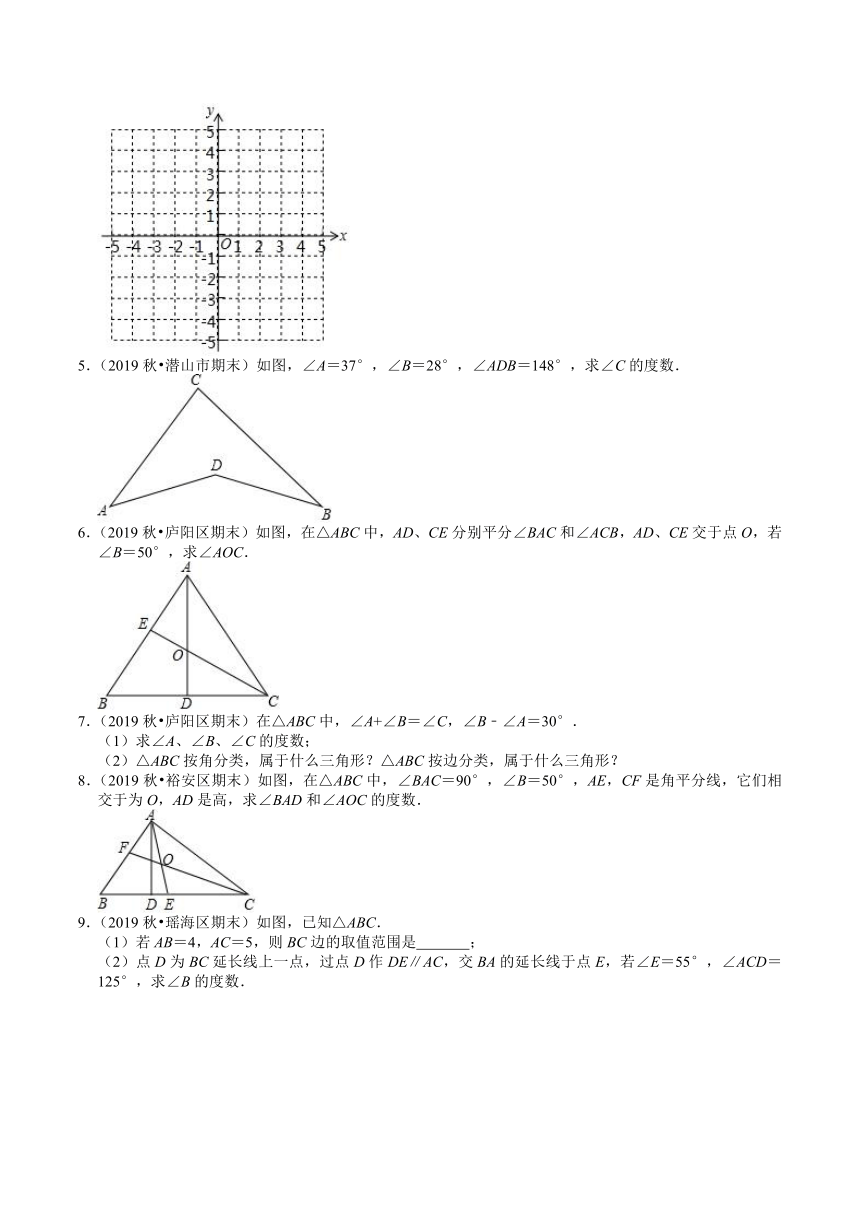
5.(2019秋?潜山市期末)如图,∠A=37°,∠B=28°,∠ADB=148°,求∠C的度数.
6.(2019秋?庐阳区期末)如图,在△ABC中,AD、CE分别平分∠BAC和∠ACB,AD、CE交于点O,若∠B=50°,求∠AOC.
7.(2019秋?庐阳区期末)在△ABC中,∠A+∠B=∠C,∠B﹣∠A=30°.
(1)求∠A、∠B、∠C的度数;
(2)△ABC按角分类,属于什么三角形?△ABC按边分类,属于什么三角形?
8.(2019秋?裕安区期末)如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.
9.(2019秋?瑶海区期末)如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是
;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
10.(2019秋?全椒县期末)已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
11.(2019秋?涡阳县期末)如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长.
12.(2019秋?全椒县期末)如图,在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
13.(2019秋?和县期末)如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,求∠E的度数.
14.(2019秋?涡阳县期末)如图,三角形AOB中,A、B两点的坐标分别为(﹣4,﹣6),(﹣6,﹣3),求三角形AOB的面积(提示:三角形AOB的面积可以看作一个梯形的面积减去一些小三角形的面积).
15.(2018秋?望江县期末)在△ABC中,AB=9,BC=2,AC=x.
(1)求x的取值范围;
(2)若△ABC的周长为偶数,则△ABC的周长为多少?
16.(2018秋?长丰县期末)已知:如图,D是AB上的一点,E是AC上一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:
(1)∠BDC的度数;
(2)∠BFC的度数.
17.(2018秋?埇桥区期末)在△ABC中,∠A=∠B+20°,∠C=∠A+50°,求△ABC各内角的度数.
18.(2018秋?包河区期末)如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD,则∠EAD=
.(直接写出结论即可)
19.(2018秋?桐城市期末)如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
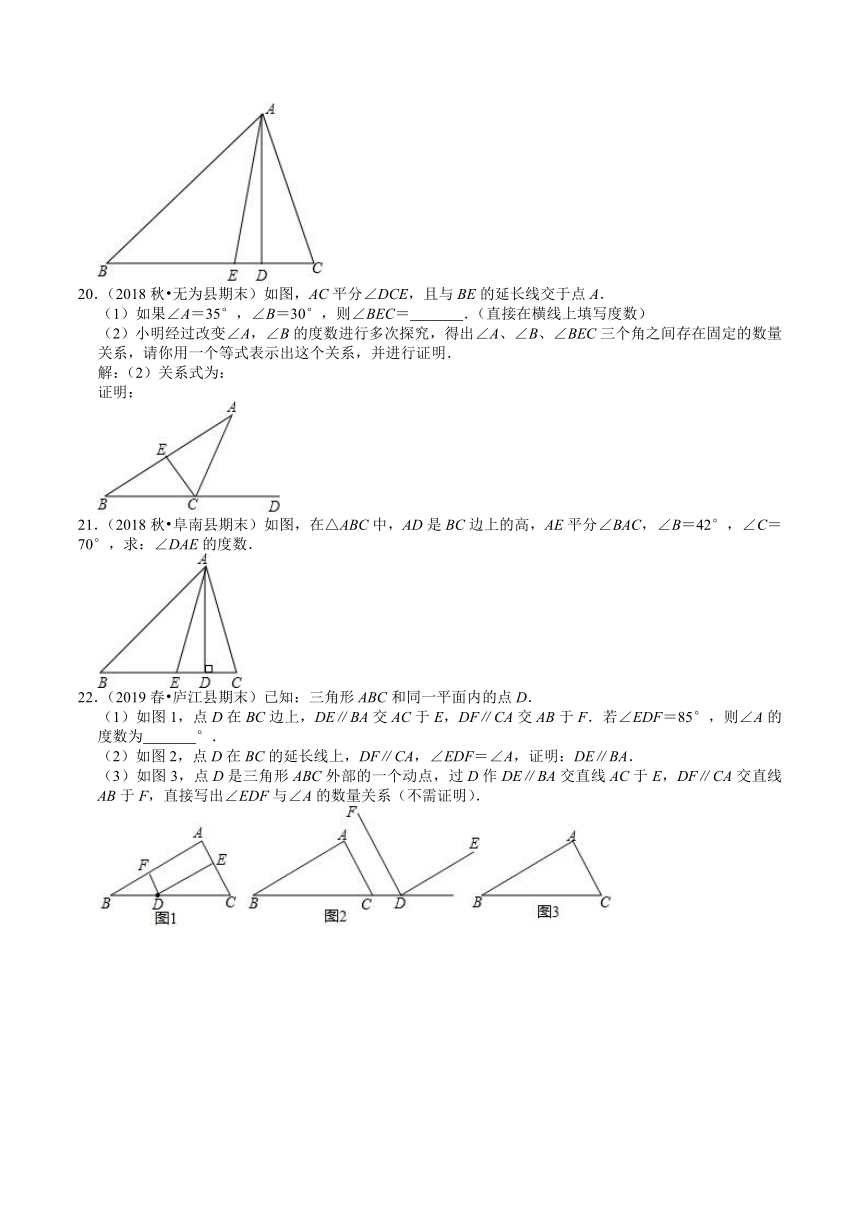
20.(2018秋?无为县期末)如图,AC平分∠DCE,且与BE的延长线交于点A.
(1)如果∠A=35°,∠B=30°,则∠BEC=
.(直接在横线上填写度数)
(2)小明经过改变∠A,∠B的度数进行多次探究,得出∠A、∠B、∠BEC三个角之间存在固定的数量关系,请你用一个等式表示出这个关系,并进行证明.
解:(2)关系式为:
证明:
21.(2018秋?阜南县期末)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=42°,∠C=70°,求:∠DAE的度数.
22.(2019春?庐江县期末)已知:三角形ABC和同一平面内的点D.
(1)如图1,点D在BC边上,DE∥BA交AC于E,DF∥CA交AB于F.若∠EDF=85°,则∠A的度数为
°.
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A,证明:DE∥BA.
(3)如图3,点D是三角形ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第13章《三角形中的边角关系、命题与证明》解答题精选
参考答案与试题解析
一.解答题(共22小题)
1.【解答】解:(1)∵∠A=75°,
∴∠ABC+∠ACB=180°﹣75°=105°,
∴∠MBC+∠MCB105°=70°,
∴∠BMC=180°﹣70°=110°.
(2)∵∠A=α,
∴∠ABC+∠ACB=180°﹣α
∴∠MBC+∠MCB(180°﹣α)=120°α
∴∠BMC=180°﹣(120°α)=60°α
2.【解答】解:(1)①∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵∠DBC∠ABC,∠DCB∠ACB,
∴∠DBC+∠DCB120°=60°,
∴∠D=180°﹣60°=120°.
②结论:∠D=90°∠A.
理由:∵∠DBC∠ABC,∠DCB∠ACB,
∴∠DBC+∠DCB(∠ABC+∠ACB)
(180°﹣∠A)
=90°∠A
∴∠D=180°﹣(90°∠A)=90°∠A.
(2)不正确.结论:∠D=90°∠A.
理由:∵∠DBC∠PBC,∠DCB∠ACB,
∴∠DBC+∠DCB(∠PBC+∠QCB)
(∠A+∠ACB+∠A+∠ABC)
(180°+∠A)
=90°∠A,
∴∠D=180°﹣(90°∠A)=90°∠A.
3.【解答】解:我写的真命题是:
已知:①②④;
求证:③
证明如下:
∵BE=FC,
∴BE+EC=CF+EC,即BC=FE,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE.
故答案为①②④;③.
4.【解答】解:如图所示,S四边形ABCD.
5.【解答】解:连接CD并延长点E,
∵∠ACD=∠ADE﹣∠A=∠ADE﹣37°,
∴∠A=37°,∠ADE=∠A+∠ACD,
同理可得:∠BCD=∠BDE﹣28°,
∵∠ACB=∠ACD+∠BCD,
∴∠ADB=148°,
∠ACB=∠ADB﹣∠A﹣∠B,
=148°﹣37°﹣28°
=83°.
6.【解答】解:∵∠ABC=50°,
∴∠BAC+∠ACB=180°﹣50°=130°,
∵AD,CE分别平分∠BAC、∠ACB,
∴∠OAC∠BAC,∠OCA∠ACB,
∴∠OAC+∠OCA(∠BAC+∠ACB)130°=65°,
在△AOC中,∠AOC=180°﹣(∠OAC+∠OCA)=180°﹣65°=115°.
7.【解答】解:(1)由题意:,
解得.
(2)∵∠C=90°,∠A=30°,∠B=60°,
∴按角分类,属于直角三角形.△ABC按边分类,属于不等边三角形.
8.【解答】解:∵AD是高,∠B=50°,
∴Rt△ABD中,∠BAD=90°﹣50°=40°,
∵∠BAC=90°,∠B=50°,
∴△ABC中,∠ACB=90°﹣50°=40°,
∵AE,CF是角平分线,
∴∠CAE∠BAC=45°,∠ACF∠ACB=20°,
∴△AOC中,∠AOC=180°﹣45°﹣20°=115°.
9.【解答】解:(1)∵AB=4,AC=5,
∴5﹣4<BC<4+5,
即1<BC<9,
故答案为:1<BC<9;
(2)∵∠ACD=125°,
∴∠ACB=180°﹣∠ACD=55°,
∵DE∥AC,
∴∠BDE=∠ACB=55°.
∵∠E=55°,
∴∠B=180°﹣∠E﹣∠BDE=180°﹣55°﹣55°=70°.
10.【解答】(1)证明:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
(2)∠MBC=∠F+∠FEC.
证明:∵BM∥AC,
∴∠MBA=∠A,、
∵∠A=∠ABC,
∴∠MBC=∠MBA+∠ABC=2∠A,
又∵∠F+∠FEC=2∠A,
∴∠MBC=∠F+∠FEC.
11.【解答】解:∵S△ABCAC?BE,S△ABCBC?AD,
∴AC?BE=BC?AD,
∴BE.
12.【解答】解:设BD=CD=x,AB=y,则AC=2BC=4x,
∵BC边上的中线AD把△ABC的周长分成60和40两部分,AC>AB,
∴AC+CD=60,AB+BD=40,
即,
解得:,
当AB=28,BC=24,AC=48时,符合三角形三边关系定理,能组成三角形,
所以AC=48,AB=28.
13.【解答】解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC∠DAC,∠ECA∠ACF;
又∵∠B=47°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC∠ACF(∠B+∠B+∠1+∠2)(外角定理),
∴∠E=180°﹣(∠DAC∠ACF)=66.5°.
14.【解答】解:S△AOB=S梯形BCDO﹣(S△ABC+S△OAD)
(3+6)×6﹣(2×34×6)
=27﹣(3+12)
=12.
15.【解答】解:(1)由题意知,9﹣2<x<9+2,即7<x<11;
(2)∵7<x<11,
∴x的值是8或9或10,
∴△ABC的周长为:9+2+8=19(舍去).
或9+2+9=20或9+2+10=21(舍去)
即该三角形的周长是20.
16.【解答】解:(1)∵∠A=62°,∠ACD=35°,
∴∠BDC=∠A+∠ACD=62°+35°=97°;
(2)∵∠ABE=20°,∠BDC=97°,
∴∠BFC=∠BDC+∠ABE=97°+20°=117°.
17.【解答】解:∵∠A=∠B+20°,∠C=∠A+50°,
∴∠C=∠B+20°+50°,
∵∠A+∠B+∠C=180°,
∴∠B+20°+∠B+∠B+20°+50°=180°,
解得:∠B=30°,
∴∠A=30°+20°=50°,
∴∠C=50°+50°=100°,
即∠A=50°,∠B=30°,∠C=100°.
18.【解答】解:(1)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=100°,
∴∠ACD=180°﹣100°=80°,
∴∠CAD=90°﹣80°=10°,
∵∠B=30°,
∴∠BAD=90°﹣30°=60°,
∴∠BAC=50°,
∵AE平分∠BAC,
∴∠CAE∠BAC=25°,
∴∠EAD=∠CAE+∠CAD=35°;
(2)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=β,
∴∠ACD=180°﹣β,
∴∠CAD=90°﹣∠ACD=β﹣90°,
∵∠B=α,
∴∠BAD=90°﹣α,
∴∠BAC=90°﹣α﹣(β﹣90°)=180°﹣α﹣β,
∵AE平分∠BAC,
∴∠CAE∠BAC=90°(α+β),
∴∠EAD=∠CAE+∠CAD=90°(α+β)+β﹣90°βα.
故答案为:βα.
19.【解答】解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°;
(2)∵AE是∠BAC的平分线,
∴∠BAE∠BAC=40°,
∴∠AED=∠BAE+∠B=40°+30°=70°;
(3)∵AD⊥BC,
∴∠ADE=90°,
∴∠EAD=∠ADE﹣AED=90°﹣70°=20°.
20.【解答】解:(1)∵∠A=35°,∠B=30°,
∴∠ACD=∠A+∠B=65°,
又∵AC平分∠DCE,
∴∠ACE=∠ACD=65°,
∴∠BEC=∠A+∠ACE=35°+65°=100°,
故答案为:100°;
(2)关系式为∠BEC=2∠A+∠B.
理由:∵AC平分∠DCE,
∴∠ACD=∠ACE,
∵∠BEC=∠A+∠ACE=∠A+∠ACD,
∵∠ACD=∠A+∠B,
∴∠BEC=∠A+∠A+∠B=2∠A+∠B.
21.【解答】解:∵∠B=42°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=68°,
∵AE平分∠BAC,
∴∠CAEBAC=34°,
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣∠ADC﹣∠C=20°,
∴∠DAE=∠CAE﹣∠CAD=34°﹣20°=14°.
22.【解答】解:(1)∵DE∥BA,DF∥CA,
∴∠A=∠DEC,∠DEC=∠EDF,
∵∠EDF=85°
∴∠A=∠EDF=85°;
故答案为:85;
(2)证明:如图1,延长BA交DF于G.
∵DF∥CA,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DE∥BA.
(3)∠EDF=∠A,∠EDF+∠A=180°,
理由:如图2,∵DE∥BA,DF∥CA,
∴∠EDF+∠E=180°,∠E+∠EAF=180°,
∴∠EDF=∠EAF=∠A;
如图3,∵DE∥BA,DF∥CA,
∴∠EDF+∠F=180°,∠F=∠CAB,
∴∠EDF+∠BAC=180°.
即∠EDF+∠A=180°,
一.解答题(共22小题)
1.(2019秋?当涂县期末)如图,在△ABC中,∠A=75°,∠ABC与∠ACB的三等分线分别交于点M、N两点.
(1)求∠BMC的度数;
(2)若设∠A=α,用α的式子表示∠BMC的度数.
2.(2019秋?埇桥区期末)(1)如图(a),BD平分∠ABC,CD平分∠ACB.
①当∠A=60°时,求∠D的度数.
②猜想∠A与∠D有什么数量关系?并证明你的结论.
(2)如图(b),BD平分外角∠CBP,CD平分外角∠BCQ,(1)中②的猜想还正确吗?如果不正确,请你直接写出正确的结论(不用写出证明过程).
3.(2019秋?临泉县期末)如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件:
①AB=DE;②AC=DF;③AB∥DE;④BE=CF.请你从中选三个作为题设,余下的一个作为结论,写出一个真命题,并加以证明.
解:我写的真命题是:
已知:
;
求证:
.(注:不能只填序号)
证明如下:
4.(2019秋?濉溪县期末)在如图所示的平面直角坐标系中,作出下列坐标的A(﹣3,2),B(0,﹣4),C(5,﹣3),D(0,1).并求出四边形ABCD的面积.
5.(2019秋?潜山市期末)如图,∠A=37°,∠B=28°,∠ADB=148°,求∠C的度数.
6.(2019秋?庐阳区期末)如图,在△ABC中,AD、CE分别平分∠BAC和∠ACB,AD、CE交于点O,若∠B=50°,求∠AOC.
7.(2019秋?庐阳区期末)在△ABC中,∠A+∠B=∠C,∠B﹣∠A=30°.
(1)求∠A、∠B、∠C的度数;
(2)△ABC按角分类,属于什么三角形?△ABC按边分类,属于什么三角形?
8.(2019秋?裕安区期末)如图,在△ABC中,∠BAC=90°,∠B=50°,AE,CF是角平分线,它们相交于为O,AD是高,求∠BAD和∠AOC的度数.
9.(2019秋?瑶海区期末)如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是
;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
10.(2019秋?全椒县期末)已知,如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB,AC和CB的延长线于点D,E,F.
(1)求证:∠F+∠FEC=2∠A;
(2)过B点作BM∥AC交FD于点M,试探究∠MBC与∠F+∠FEC的数量关系,并证明你的结论.
11.(2019秋?涡阳县期末)如图,在△ABC中,AC=6,BC=8,AD⊥BC于D,AD=5,BE⊥AC于E,求BE的长.
12.(2019秋?全椒县期末)如图,在△ABC中(AC>AB),AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,求AC和AB的长.
13.(2019秋?和县期末)如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,求∠E的度数.
14.(2019秋?涡阳县期末)如图,三角形AOB中,A、B两点的坐标分别为(﹣4,﹣6),(﹣6,﹣3),求三角形AOB的面积(提示:三角形AOB的面积可以看作一个梯形的面积减去一些小三角形的面积).
15.(2018秋?望江县期末)在△ABC中,AB=9,BC=2,AC=x.
(1)求x的取值范围;
(2)若△ABC的周长为偶数,则△ABC的周长为多少?
16.(2018秋?长丰县期末)已知:如图,D是AB上的一点,E是AC上一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:
(1)∠BDC的度数;
(2)∠BFC的度数.
17.(2018秋?埇桥区期末)在△ABC中,∠A=∠B+20°,∠C=∠A+50°,求△ABC各内角的度数.
18.(2018秋?包河区期末)如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD,则∠EAD=
.(直接写出结论即可)
19.(2018秋?桐城市期末)如图,△ABC中,AD⊥BC于点D,AE是∠BAC的平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
20.(2018秋?无为县期末)如图,AC平分∠DCE,且与BE的延长线交于点A.
(1)如果∠A=35°,∠B=30°,则∠BEC=
.(直接在横线上填写度数)
(2)小明经过改变∠A,∠B的度数进行多次探究,得出∠A、∠B、∠BEC三个角之间存在固定的数量关系,请你用一个等式表示出这个关系,并进行证明.
解:(2)关系式为:
证明:
21.(2018秋?阜南县期末)如图,在△ABC中,AD是BC边上的高,AE平分∠BAC,∠B=42°,∠C=70°,求:∠DAE的度数.
22.(2019春?庐江县期末)已知:三角形ABC和同一平面内的点D.
(1)如图1,点D在BC边上,DE∥BA交AC于E,DF∥CA交AB于F.若∠EDF=85°,则∠A的度数为
°.
(2)如图2,点D在BC的延长线上,DF∥CA,∠EDF=∠A,证明:DE∥BA.
(3)如图3,点D是三角形ABC外部的一个动点,过D作DE∥BA交直线AC于E,DF∥CA交直线AB于F,直接写出∠EDF与∠A的数量关系(不需证明).
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第13章《三角形中的边角关系、命题与证明》解答题精选
参考答案与试题解析
一.解答题(共22小题)
1.【解答】解:(1)∵∠A=75°,
∴∠ABC+∠ACB=180°﹣75°=105°,
∴∠MBC+∠MCB105°=70°,
∴∠BMC=180°﹣70°=110°.
(2)∵∠A=α,
∴∠ABC+∠ACB=180°﹣α
∴∠MBC+∠MCB(180°﹣α)=120°α
∴∠BMC=180°﹣(120°α)=60°α
2.【解答】解:(1)①∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵∠DBC∠ABC,∠DCB∠ACB,
∴∠DBC+∠DCB120°=60°,
∴∠D=180°﹣60°=120°.
②结论:∠D=90°∠A.
理由:∵∠DBC∠ABC,∠DCB∠ACB,
∴∠DBC+∠DCB(∠ABC+∠ACB)
(180°﹣∠A)
=90°∠A
∴∠D=180°﹣(90°∠A)=90°∠A.
(2)不正确.结论:∠D=90°∠A.
理由:∵∠DBC∠PBC,∠DCB∠ACB,
∴∠DBC+∠DCB(∠PBC+∠QCB)
(∠A+∠ACB+∠A+∠ABC)
(180°+∠A)
=90°∠A,
∴∠D=180°﹣(90°∠A)=90°∠A.
3.【解答】解:我写的真命题是:
已知:①②④;
求证:③
证明如下:
∵BE=FC,
∴BE+EC=CF+EC,即BC=FE,
在△ABC和△DEF中
,
∴△ABC≌△DEF(SSS),
∴∠B=∠DEF,
∴AB∥DE.
故答案为①②④;③.
4.【解答】解:如图所示,S四边形ABCD.
5.【解答】解:连接CD并延长点E,
∵∠ACD=∠ADE﹣∠A=∠ADE﹣37°,
∴∠A=37°,∠ADE=∠A+∠ACD,
同理可得:∠BCD=∠BDE﹣28°,
∵∠ACB=∠ACD+∠BCD,
∴∠ADB=148°,
∠ACB=∠ADB﹣∠A﹣∠B,
=148°﹣37°﹣28°
=83°.
6.【解答】解:∵∠ABC=50°,
∴∠BAC+∠ACB=180°﹣50°=130°,
∵AD,CE分别平分∠BAC、∠ACB,
∴∠OAC∠BAC,∠OCA∠ACB,
∴∠OAC+∠OCA(∠BAC+∠ACB)130°=65°,
在△AOC中,∠AOC=180°﹣(∠OAC+∠OCA)=180°﹣65°=115°.
7.【解答】解:(1)由题意:,
解得.
(2)∵∠C=90°,∠A=30°,∠B=60°,
∴按角分类,属于直角三角形.△ABC按边分类,属于不等边三角形.
8.【解答】解:∵AD是高,∠B=50°,
∴Rt△ABD中,∠BAD=90°﹣50°=40°,
∵∠BAC=90°,∠B=50°,
∴△ABC中,∠ACB=90°﹣50°=40°,
∵AE,CF是角平分线,
∴∠CAE∠BAC=45°,∠ACF∠ACB=20°,
∴△AOC中,∠AOC=180°﹣45°﹣20°=115°.
9.【解答】解:(1)∵AB=4,AC=5,
∴5﹣4<BC<4+5,
即1<BC<9,
故答案为:1<BC<9;
(2)∵∠ACD=125°,
∴∠ACB=180°﹣∠ACD=55°,
∵DE∥AC,
∴∠BDE=∠ACB=55°.
∵∠E=55°,
∴∠B=180°﹣∠E﹣∠BDE=180°﹣55°﹣55°=70°.
10.【解答】(1)证明:∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,
∴∠F+∠FEC=∠F+∠A+∠ADE,
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC,
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
(2)∠MBC=∠F+∠FEC.
证明:∵BM∥AC,
∴∠MBA=∠A,、
∵∠A=∠ABC,
∴∠MBC=∠MBA+∠ABC=2∠A,
又∵∠F+∠FEC=2∠A,
∴∠MBC=∠F+∠FEC.
11.【解答】解:∵S△ABCAC?BE,S△ABCBC?AD,
∴AC?BE=BC?AD,
∴BE.
12.【解答】解:设BD=CD=x,AB=y,则AC=2BC=4x,
∵BC边上的中线AD把△ABC的周长分成60和40两部分,AC>AB,
∴AC+CD=60,AB+BD=40,
即,
解得:,
当AB=28,BC=24,AC=48时,符合三角形三边关系定理,能组成三角形,
所以AC=48,AB=28.
13.【解答】解:∵三角形的外角∠DAC和∠ACF的平分线交于点E,
∴∠EAC∠DAC,∠ECA∠ACF;
又∵∠B=47°(已知),∠B+∠1+∠2=180°(三角形内角和定理),
∴∠DAC∠ACF(∠B+∠B+∠1+∠2)(外角定理),
∴∠E=180°﹣(∠DAC∠ACF)=66.5°.
14.【解答】解:S△AOB=S梯形BCDO﹣(S△ABC+S△OAD)
(3+6)×6﹣(2×34×6)
=27﹣(3+12)
=12.
15.【解答】解:(1)由题意知,9﹣2<x<9+2,即7<x<11;
(2)∵7<x<11,
∴x的值是8或9或10,
∴△ABC的周长为:9+2+8=19(舍去).
或9+2+9=20或9+2+10=21(舍去)
即该三角形的周长是20.
16.【解答】解:(1)∵∠A=62°,∠ACD=35°,
∴∠BDC=∠A+∠ACD=62°+35°=97°;
(2)∵∠ABE=20°,∠BDC=97°,
∴∠BFC=∠BDC+∠ABE=97°+20°=117°.
17.【解答】解:∵∠A=∠B+20°,∠C=∠A+50°,
∴∠C=∠B+20°+50°,
∵∠A+∠B+∠C=180°,
∴∠B+20°+∠B+∠B+20°+50°=180°,
解得:∠B=30°,
∴∠A=30°+20°=50°,
∴∠C=50°+50°=100°,
即∠A=50°,∠B=30°,∠C=100°.
18.【解答】解:(1)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=100°,
∴∠ACD=180°﹣100°=80°,
∴∠CAD=90°﹣80°=10°,
∵∠B=30°,
∴∠BAD=90°﹣30°=60°,
∴∠BAC=50°,
∵AE平分∠BAC,
∴∠CAE∠BAC=25°,
∴∠EAD=∠CAE+∠CAD=35°;
(2)∵AD⊥BC,
∴∠D=90°,
∵∠ACB=β,
∴∠ACD=180°﹣β,
∴∠CAD=90°﹣∠ACD=β﹣90°,
∵∠B=α,
∴∠BAD=90°﹣α,
∴∠BAC=90°﹣α﹣(β﹣90°)=180°﹣α﹣β,
∵AE平分∠BAC,
∴∠CAE∠BAC=90°(α+β),
∴∠EAD=∠CAE+∠CAD=90°(α+β)+β﹣90°βα.
故答案为:βα.
19.【解答】解:(1)∵∠B=30°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=80°;
(2)∵AE是∠BAC的平分线,
∴∠BAE∠BAC=40°,
∴∠AED=∠BAE+∠B=40°+30°=70°;
(3)∵AD⊥BC,
∴∠ADE=90°,
∴∠EAD=∠ADE﹣AED=90°﹣70°=20°.
20.【解答】解:(1)∵∠A=35°,∠B=30°,
∴∠ACD=∠A+∠B=65°,
又∵AC平分∠DCE,
∴∠ACE=∠ACD=65°,
∴∠BEC=∠A+∠ACE=35°+65°=100°,
故答案为:100°;
(2)关系式为∠BEC=2∠A+∠B.
理由:∵AC平分∠DCE,
∴∠ACD=∠ACE,
∵∠BEC=∠A+∠ACE=∠A+∠ACD,
∵∠ACD=∠A+∠B,
∴∠BEC=∠A+∠A+∠B=2∠A+∠B.
21.【解答】解:∵∠B=42°,∠C=70°,
∴∠BAC=180°﹣∠B﹣∠C=68°,
∵AE平分∠BAC,
∴∠CAEBAC=34°,
∵AD是BC边上的高,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°﹣∠ADC﹣∠C=20°,
∴∠DAE=∠CAE﹣∠CAD=34°﹣20°=14°.
22.【解答】解:(1)∵DE∥BA,DF∥CA,
∴∠A=∠DEC,∠DEC=∠EDF,
∵∠EDF=85°
∴∠A=∠EDF=85°;
故答案为:85;
(2)证明:如图1,延长BA交DF于G.
∵DF∥CA,
∴∠2=∠3.
又∵∠1=∠2,
∴∠1=∠3.
∴DE∥BA.
(3)∠EDF=∠A,∠EDF+∠A=180°,
理由:如图2,∵DE∥BA,DF∥CA,
∴∠EDF+∠E=180°,∠E+∠EAF=180°,
∴∠EDF=∠EAF=∠A;
如图3,∵DE∥BA,DF∥CA,
∴∠EDF+∠F=180°,∠F=∠CAB,
∴∠EDF+∠BAC=180°.
即∠EDF+∠A=180°,
