2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第12章《一次函数》填空题精选(Word版 含答案)
文档属性
| 名称 | 2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第12章《一次函数》填空题精选(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 74.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 14:31:29 | ||
图片预览


文档简介
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第12章《一次函数》填空题精选
一.填空题(共27小题)
1.(2020春?谢家集区期末)已知一次函数图象与直线y=2x+1平行,且过点(﹣1,2),那么此一次函数的解析式为 .
2.(2020春?谢家集区期末)已知一次函数y=(k﹣3)x+4,若y随x的增大而减小,则k的值可以是 (写出一个答案即可).
3.(2019秋?宿松县校级期末)已知一次函数y=kx+b(k≠0)的图象经过点A(﹣2,3),且与x轴的交点B到坐标原点的距离为1,则这个一次函数的表达式为 .
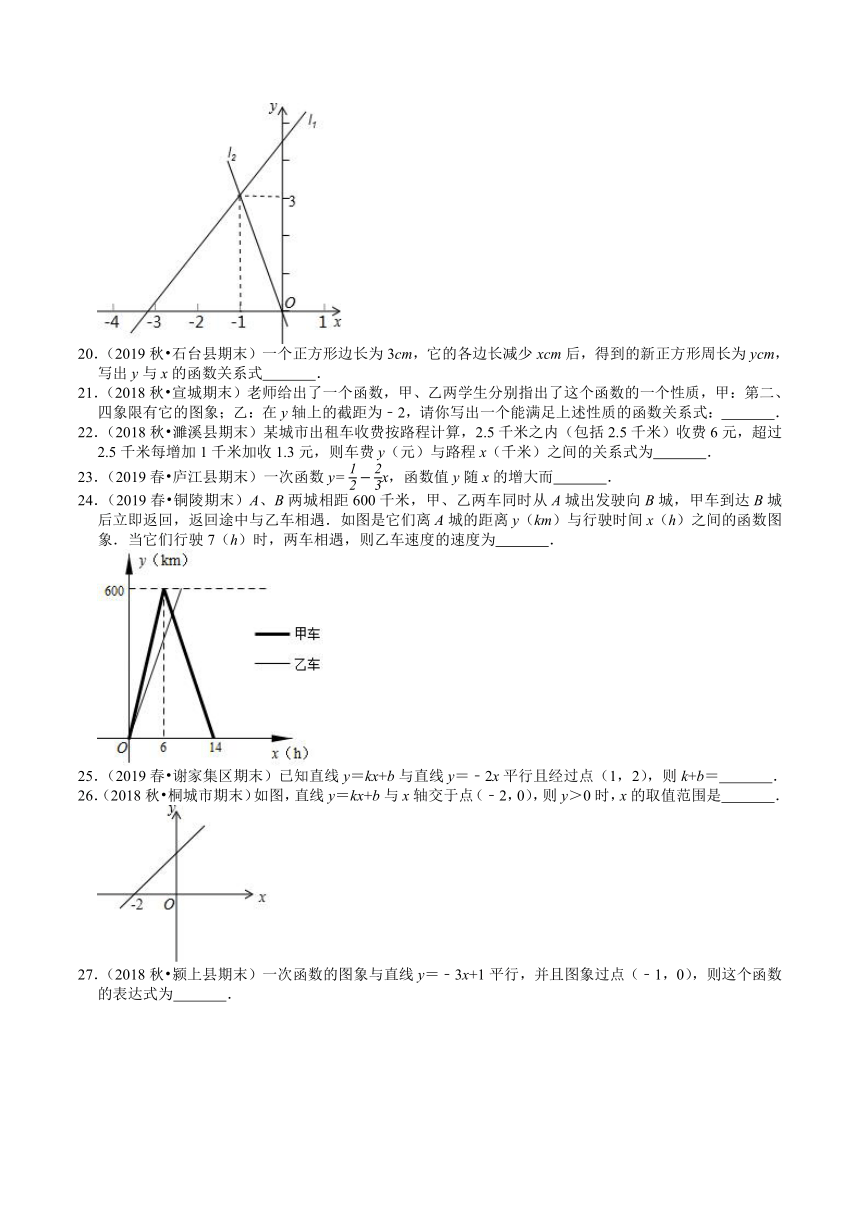
4.(2020春?芜湖期末)甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论正确的是 .
①a的值为40;
②当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20;
③乙车比甲车早1.5h到达B地;
④乙车行驶0.5h或2.5h时,两车恰相距40km.
5.(2020春?铜陵期末)如图1所示,动点P在矩形边上,从点A出发,以相同的速度,沿着A﹣B﹣C﹣D﹣A方向运动到点A处停止,设点P运动的路程为x,△PAB的面积为y,如果y与x的函数图象如图2所示,则矩形的面积是 .
6.(2020春?铜陵期末)已知关于x的一次函数的图象不经过第二象限但经过点(0,﹣2).你认为符合要求的一次函数的表达式可以是 (写一个函数即可).
7.(2019秋?宿松县期末)已知直线y=kx﹣4与直线y=﹣x+2相交于x轴上一点,则k= .
8.(2019秋?石台县期末)已知一次函数y=kx+b,当﹣3≤x≤1时,﹣1≤y≤8,则此函数与y轴的交点坐标是 .
9.(2019秋?宣城期末)已知y+4与x﹣3成正比例,且x=5时y=4,则当y=5时,x的值为 .
10.(2019秋?当涂县期末)一次函数y=3x的图象沿y轴向上平移3个单位长度,则平移后的图象所对应的函数表达式为 .
11.(2019秋?肥东县期末)如图,已知A(4,0),B(2,4),若直线y=kx+2与线段AB无公共点,则k的取值范围为 .
12.(2019秋?濉溪县期末)当m= 时,直线y=﹣2x+m与直线y=4x﹣2的交点在x轴上.
13.(2019秋?庐阳区期末)在平面直角坐标系中,先将函数y=2x﹣2的图象关于x轴作轴对称变换后,再沿x轴水平向右平移2个单位后,再将所得的图象关于y轴作轴对称变换,则经过三次变换后所得的图象对应的解析式为 .
14.(2020春?和县期末)如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的不等3x+b>ax﹣2的解集为 .
15.(2019秋?东至县期末)新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[3,m﹣2]的一次函数是正比例函数,则点(1﹣m,1+m)在第 象限.
16.(2020春?庐江县期末)如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是 .
17.(2019秋?宿州期末)已知某直线经过点A(0,2),且与两坐标轴围成的三角形面积为2.则该直线的一次函数表达式是 .
18.(2019秋?当涂县期末)如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是 .
19.(2019秋?包河区期末)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为 .
20.(2019秋?石台县期末)一个正方形边长为3cm,它的各边长减少xcm后,得到的新正方形周长为ycm,写出y与x的函数关系式 .
21.(2018秋?宣城期末)老师给出了一个函数,甲、乙两学生分别指出了这个函数的一个性质,甲:第二、四象限有它的图象;乙:在y轴上的截距为﹣2,请你写出一个能满足上述性质的函数关系式: .
22.(2018秋?濉溪县期末)某城市出租车收费按路程计算,2.5千米之内(包括2.5千米)收费6元,超过2.5千米每增加1千米加收1.3元,则车费y(元)与路程x(千米)之间的关系式为 .
23.(2019春?庐江县期末)一次函数y=12-23x,函数值y随x的增大而 .
24.(2019春?铜陵期末)A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回,返回途中与乙车相遇.如图是它们离A城的距离y(km)与行驶时间x(h)之间的函数图象.当它们行驶7(h)时,两车相遇,则乙车速度的速度为 .
25.(2019春?谢家集区期末)已知直线y=kx+b与直线y=﹣2x平行且经过点(1,2),则k+b= .
26.(2018秋?桐城市期末)如图,直线y=kx+b与x轴交于点(﹣2,0),则y>0时,x的取值范围是 .
27.(2018秋?颍上县期末)一次函数的图象与直线y=﹣3x+1平行,并且图象过点(﹣1,0),则这个函数的表达式为 .
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第12章《一次函数》填空题精选
参考答案与试题解析
一.填空题(共27小题)
1.【解答】解:设一次函数解析式为y=kx+b,
∵一次函数的图象与直线y=2x+1平行,
∴k=2,
∴y=2x+b,
把(﹣1,2)代入,2=2×(﹣1)+b,
解得:b=4,
∴y=2x+4.
故答案为:y=2x+4.
2.【解答】解:∵一次函数y=(k﹣3)x+4,若y随x的增大而减小,
∴k﹣3<0,
解得k<3,
∴k可以取2.
故答案为:2(答案不唯一).
3.【解答】解:根据题意点B坐标为(﹣1,0)或(1,0),分两种情况:
(1)一次函数图象经过点(﹣2,3)和(﹣1,0)时,
代入y=kx+b得:-2k+b=3-k+b=0,
解得:k=-3b=-3,
此时一次函数表达式为y=﹣3x﹣3;
(2)一次函数图象经过点(﹣2,3)和(1,0)时,
代入y=kx+b得:-2k+b=3k+b=0,
解得:k=-1b=1,
此时一次函数表达式为y=﹣x+1.
故答案为:y=﹣3x﹣3或y=﹣x+1.
4.【解答】解:a=120÷(3.5﹣0.5)×1=40,故①正确;
当1.5<x≤7时,设甲车行驶路程y与时间x的函数表达式为y=kx+b,
1.5k+b=403.5k+b=120,得k=40b=-20,
即当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20,故②正确;
乙车的速度为:120÷(3.5﹣2)=80(km/h),
乙车从A地到B地用的时间为:260÷80=3.25(h),
乙车比甲车早[3.5+(260﹣120)÷40]﹣(2+3.25)=1.75h到达B地,故③错误;
当乙车行驶0.5h时,两车相距[40+(2+0.5﹣1.5)×40]﹣80×0.5=40(km),
当乙车行驶2.5h时,两车相距80×2.5﹣[40+(2﹣1.5+2.5)×40]=40(km),
故④正确;
故答案为:①②④.
5.【解答】解:从图2和已知可知:AB=4,BC=10﹣4=6,
所以矩形ABCD的面积是4×6=24,
故答案为:24.
6.【解答】解:∵关于x的一次函数的图象不经过第二象限但经过点(0,﹣2).
∴k>0;b=﹣2.
∴该一次函数的表达式可为:y=x﹣2(答案不唯一)
故答案为:y=x﹣2.
7.【解答】解:∵直线y=﹣x+2与x轴相交,
∴﹣x+2=0,
∴x=2,
∴与x轴的交点坐标为(2,0),
把(2,0)代入y=kx﹣4中:2k﹣4=0,
∴k=2.
故答案为:2.
8.【解答】解:①将x=1,y=8代入得:8=k+b,将x=﹣3,y=﹣1代入得:﹣1=﹣3k+b,
解得:k=94,b=234;
∴函数解析式为y=94x+234,
∴当x=0时,y=234,
∴函数与y轴的交点坐标(0,234);
②将x=1,y=﹣1,代入得:﹣1=k+b,将x=﹣3,y=8代入得:8=﹣3k+b,
解得:k=-94,b=54,
∴函数解析式为y=-94x+54,
∴当x=0时,y=54,
∴函数与y轴的交点坐标(0,54);
故答案为:(0,234)或(0,54).
9.【解答】解:∵y+4与x﹣3成正比例,
∴y+4=k(x﹣3),
∵x=5时,y=4,
∴8=k?(5﹣3),
解得:k=4,
故y+4=4(x﹣3),
当y=5时,
9=4(x﹣3),
解得:x=214.
故答案为:214.
10.【解答】解:∵将一次函数y=3x的图象沿y轴向上平移个单位长度,
∴平移后所得图象对应的函数关系式为:y=3x+3,
故答案为y=3x+3.
11.【解答】解:当k>0时,y=kx+2过B(2,4)时,
4=2k+2,解得k=1,
∴直线y=kx+2与线段AB无公共点,则k>1;
当k<0时,y=kx+2过A(4,0),
0=4k+2,解得k=-12,
∴直线y=kx+2与线段AB无公共点,则k<-12.
综上,满足条件的k的取值范围是k>1或k<-12;
故答案为k>1或k<-12.
12.【解答】解:当y=4x﹣2=0时,x=12,
∴直线y=4x﹣2与x轴的交点坐标为(12,0).
∵直线y=﹣2x+m与直线y=4x﹣2的交点在x轴上,
∴直线y=﹣2x+m与x轴的交点坐标为(12,0),
∴0=﹣2×12+m,
解得:m=1.
故答案为:1.
13.【解答】解:函数y=2x﹣2的图象关于x轴作轴对称变换,
则所得函数为﹣y=2x﹣2,即y=﹣2x+2;
再沿x轴水平向右平移2个单位后,
则所得函数为y=﹣2(x﹣2)+2=﹣2x+6;
再将所得的图象关于y轴作轴对称变换,
则所得抛物线为y=﹣2(﹣x)+6=2x+6,
即y=2x+6.
故答案为y=2x+6.
14.【解答】解:从图象得到,当x>﹣2时,y=3x+b的图象对应的点在函数y=ax﹣2的图象上方,
∴不等式3x+b>ax﹣2的解集为:x>﹣2.
故答案为x>﹣2.
15.【解答】解:∵“关联数”为[3,m﹣2]的一次函数是正比例函数,
∴y=3x+m﹣2是正比例函数,
∴m﹣2=0,
解得:m=2,
则1﹣m=﹣1,1+m=3,
故点(1﹣m,1+m)在第二象限.
故答案为:二.
16.【解答】解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
∴不等式 3x+b>ax﹣3的解集是x>﹣2,
故答案为:x>﹣2.
17.【解答】解:设直线解析式为y=kx+b,
把(0,2)代入得b=2,
所以y=kx+2,
把y=0代入得x=-2k,
所以12×2×|-2k|=2,
解得:k=1或﹣1,
所以所求的直线解析式为y=x+2或y=﹣x+2.
故答案为:y=x+2或y=﹣x+2.
18.【解答】解:当x>1时,x+b>kx+4,
即不等式x+b>kx+4的解集为x>1.
故答案为x>1.
19.【解答】解:当x<﹣1时,k2x>k1x+b,
所以不等式k2x>k1x+b的解集为x<﹣1.
故答案为x<﹣1.
20.【解答】解:各边长减少xcm后,得到的新正方形的边长是3﹣xcm,
则周长y=4(3﹣x).
故答案是:y=4(3﹣x).
21.【解答】解:设此函数为一次函数,解析式为y=kx+b,
∵第二、四象限有它的图象,
∴k<0,可取﹣3,
∵在y轴上的截距为﹣2,
∴b=﹣2,
∴此函数解析式为y=﹣3x﹣2,
故答案为:y=﹣3x﹣2.
22.【解答】解:根据题意得:
①当0<x≤2.5时,y=6;
②当x>2.5时,y=6+1.3(x﹣2.5)=1.3x+2.75;
∴车费y(元)与路程x(千米)之间的函数关系式为:y=6(0<x≤2.5)1.3x+2.75(x>2.5),
故答案为:y=6(0<x≤2.5)1.3x+2.75(x>2.5).
23.【解答】解:因为一次函数y=12-23x中k=-23<0.
所以函数值y随x的增大而 减小.
故答案是;减小.
24.【解答】解:甲返程的速度为:600÷(14﹣6)=75,
设乙车的速度为x,
由题意得:600=7x+75,
解得:x=75,
故答案为75千米/小时.
25.【解答】解:∵直线y=kx+b与直线y=2x平行,
∴k=2,
∴y=2x+b,
把点A(1,2)代入y=2x+b得2+b=2,解得b=0;
∴k+b=2,
故答案为:2.
26.【解答】解:∵直线y=kx+b与x轴交于点(﹣2,0),
∴当y>0时,x的取值范围是x>﹣2,
故答案为:x>﹣2.
27.【解答】解:设所求一次函数解析式为y=﹣3x+b,
把(﹣1,0)代入得:0=3+b,
解得:b=﹣3,
则一次函数解析式为y=﹣3x﹣3,
故答案为:y=﹣3x﹣3.
一.填空题(共27小题)
1.(2020春?谢家集区期末)已知一次函数图象与直线y=2x+1平行,且过点(﹣1,2),那么此一次函数的解析式为 .
2.(2020春?谢家集区期末)已知一次函数y=(k﹣3)x+4,若y随x的增大而减小,则k的值可以是 (写出一个答案即可).
3.(2019秋?宿松县校级期末)已知一次函数y=kx+b(k≠0)的图象经过点A(﹣2,3),且与x轴的交点B到坐标原点的距离为1,则这个一次函数的表达式为 .
4.(2020春?芜湖期末)甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论正确的是 .
①a的值为40;
②当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20;
③乙车比甲车早1.5h到达B地;
④乙车行驶0.5h或2.5h时,两车恰相距40km.
5.(2020春?铜陵期末)如图1所示,动点P在矩形边上,从点A出发,以相同的速度,沿着A﹣B﹣C﹣D﹣A方向运动到点A处停止,设点P运动的路程为x,△PAB的面积为y,如果y与x的函数图象如图2所示,则矩形的面积是 .
6.(2020春?铜陵期末)已知关于x的一次函数的图象不经过第二象限但经过点(0,﹣2).你认为符合要求的一次函数的表达式可以是 (写一个函数即可).
7.(2019秋?宿松县期末)已知直线y=kx﹣4与直线y=﹣x+2相交于x轴上一点,则k= .
8.(2019秋?石台县期末)已知一次函数y=kx+b,当﹣3≤x≤1时,﹣1≤y≤8,则此函数与y轴的交点坐标是 .
9.(2019秋?宣城期末)已知y+4与x﹣3成正比例,且x=5时y=4,则当y=5时,x的值为 .
10.(2019秋?当涂县期末)一次函数y=3x的图象沿y轴向上平移3个单位长度,则平移后的图象所对应的函数表达式为 .
11.(2019秋?肥东县期末)如图,已知A(4,0),B(2,4),若直线y=kx+2与线段AB无公共点,则k的取值范围为 .
12.(2019秋?濉溪县期末)当m= 时,直线y=﹣2x+m与直线y=4x﹣2的交点在x轴上.
13.(2019秋?庐阳区期末)在平面直角坐标系中,先将函数y=2x﹣2的图象关于x轴作轴对称变换后,再沿x轴水平向右平移2个单位后,再将所得的图象关于y轴作轴对称变换,则经过三次变换后所得的图象对应的解析式为 .
14.(2020春?和县期末)如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,则关于x的不等3x+b>ax﹣2的解集为 .
15.(2019秋?东至县期末)新定义:[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”为[3,m﹣2]的一次函数是正比例函数,则点(1﹣m,1+m)在第 象限.
16.(2020春?庐江县期末)如图,已知函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),则根据图象可得不等式3x+b>ax﹣3的解集是 .
17.(2019秋?宿州期末)已知某直线经过点A(0,2),且与两坐标轴围成的三角形面积为2.则该直线的一次函数表达式是 .
18.(2019秋?当涂县期末)如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集是 .
19.(2019秋?包河区期末)直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为 .
20.(2019秋?石台县期末)一个正方形边长为3cm,它的各边长减少xcm后,得到的新正方形周长为ycm,写出y与x的函数关系式 .
21.(2018秋?宣城期末)老师给出了一个函数,甲、乙两学生分别指出了这个函数的一个性质,甲:第二、四象限有它的图象;乙:在y轴上的截距为﹣2,请你写出一个能满足上述性质的函数关系式: .
22.(2018秋?濉溪县期末)某城市出租车收费按路程计算,2.5千米之内(包括2.5千米)收费6元,超过2.5千米每增加1千米加收1.3元,则车费y(元)与路程x(千米)之间的关系式为 .
23.(2019春?庐江县期末)一次函数y=12-23x,函数值y随x的增大而 .
24.(2019春?铜陵期末)A、B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回,返回途中与乙车相遇.如图是它们离A城的距离y(km)与行驶时间x(h)之间的函数图象.当它们行驶7(h)时,两车相遇,则乙车速度的速度为 .
25.(2019春?谢家集区期末)已知直线y=kx+b与直线y=﹣2x平行且经过点(1,2),则k+b= .
26.(2018秋?桐城市期末)如图,直线y=kx+b与x轴交于点(﹣2,0),则y>0时,x的取值范围是 .
27.(2018秋?颍上县期末)一次函数的图象与直线y=﹣3x+1平行,并且图象过点(﹣1,0),则这个函数的表达式为 .
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第12章《一次函数》填空题精选
参考答案与试题解析
一.填空题(共27小题)
1.【解答】解:设一次函数解析式为y=kx+b,
∵一次函数的图象与直线y=2x+1平行,
∴k=2,
∴y=2x+b,
把(﹣1,2)代入,2=2×(﹣1)+b,
解得:b=4,
∴y=2x+4.
故答案为:y=2x+4.
2.【解答】解:∵一次函数y=(k﹣3)x+4,若y随x的增大而减小,
∴k﹣3<0,
解得k<3,
∴k可以取2.
故答案为:2(答案不唯一).
3.【解答】解:根据题意点B坐标为(﹣1,0)或(1,0),分两种情况:
(1)一次函数图象经过点(﹣2,3)和(﹣1,0)时,
代入y=kx+b得:-2k+b=3-k+b=0,
解得:k=-3b=-3,
此时一次函数表达式为y=﹣3x﹣3;
(2)一次函数图象经过点(﹣2,3)和(1,0)时,
代入y=kx+b得:-2k+b=3k+b=0,
解得:k=-1b=1,
此时一次函数表达式为y=﹣x+1.
故答案为:y=﹣3x﹣3或y=﹣x+1.
4.【解答】解:a=120÷(3.5﹣0.5)×1=40,故①正确;
当1.5<x≤7时,设甲车行驶路程y与时间x的函数表达式为y=kx+b,
1.5k+b=403.5k+b=120,得k=40b=-20,
即当1.5<x≤7时,甲车行驶路程y与时间x的函数表达式为y=40x﹣20,故②正确;
乙车的速度为:120÷(3.5﹣2)=80(km/h),
乙车从A地到B地用的时间为:260÷80=3.25(h),
乙车比甲车早[3.5+(260﹣120)÷40]﹣(2+3.25)=1.75h到达B地,故③错误;
当乙车行驶0.5h时,两车相距[40+(2+0.5﹣1.5)×40]﹣80×0.5=40(km),
当乙车行驶2.5h时,两车相距80×2.5﹣[40+(2﹣1.5+2.5)×40]=40(km),
故④正确;
故答案为:①②④.
5.【解答】解:从图2和已知可知:AB=4,BC=10﹣4=6,
所以矩形ABCD的面积是4×6=24,
故答案为:24.
6.【解答】解:∵关于x的一次函数的图象不经过第二象限但经过点(0,﹣2).
∴k>0;b=﹣2.
∴该一次函数的表达式可为:y=x﹣2(答案不唯一)
故答案为:y=x﹣2.
7.【解答】解:∵直线y=﹣x+2与x轴相交,
∴﹣x+2=0,
∴x=2,
∴与x轴的交点坐标为(2,0),
把(2,0)代入y=kx﹣4中:2k﹣4=0,
∴k=2.
故答案为:2.
8.【解答】解:①将x=1,y=8代入得:8=k+b,将x=﹣3,y=﹣1代入得:﹣1=﹣3k+b,
解得:k=94,b=234;
∴函数解析式为y=94x+234,
∴当x=0时,y=234,
∴函数与y轴的交点坐标(0,234);
②将x=1,y=﹣1,代入得:﹣1=k+b,将x=﹣3,y=8代入得:8=﹣3k+b,
解得:k=-94,b=54,
∴函数解析式为y=-94x+54,
∴当x=0时,y=54,
∴函数与y轴的交点坐标(0,54);
故答案为:(0,234)或(0,54).
9.【解答】解:∵y+4与x﹣3成正比例,
∴y+4=k(x﹣3),
∵x=5时,y=4,
∴8=k?(5﹣3),
解得:k=4,
故y+4=4(x﹣3),
当y=5时,
9=4(x﹣3),
解得:x=214.
故答案为:214.
10.【解答】解:∵将一次函数y=3x的图象沿y轴向上平移个单位长度,
∴平移后所得图象对应的函数关系式为:y=3x+3,
故答案为y=3x+3.
11.【解答】解:当k>0时,y=kx+2过B(2,4)时,
4=2k+2,解得k=1,
∴直线y=kx+2与线段AB无公共点,则k>1;
当k<0时,y=kx+2过A(4,0),
0=4k+2,解得k=-12,
∴直线y=kx+2与线段AB无公共点,则k<-12.
综上,满足条件的k的取值范围是k>1或k<-12;
故答案为k>1或k<-12.
12.【解答】解:当y=4x﹣2=0时,x=12,
∴直线y=4x﹣2与x轴的交点坐标为(12,0).
∵直线y=﹣2x+m与直线y=4x﹣2的交点在x轴上,
∴直线y=﹣2x+m与x轴的交点坐标为(12,0),
∴0=﹣2×12+m,
解得:m=1.
故答案为:1.
13.【解答】解:函数y=2x﹣2的图象关于x轴作轴对称变换,
则所得函数为﹣y=2x﹣2,即y=﹣2x+2;
再沿x轴水平向右平移2个单位后,
则所得函数为y=﹣2(x﹣2)+2=﹣2x+6;
再将所得的图象关于y轴作轴对称变换,
则所得抛物线为y=﹣2(﹣x)+6=2x+6,
即y=2x+6.
故答案为y=2x+6.
14.【解答】解:从图象得到,当x>﹣2时,y=3x+b的图象对应的点在函数y=ax﹣2的图象上方,
∴不等式3x+b>ax﹣2的解集为:x>﹣2.
故答案为x>﹣2.
15.【解答】解:∵“关联数”为[3,m﹣2]的一次函数是正比例函数,
∴y=3x+m﹣2是正比例函数,
∴m﹣2=0,
解得:m=2,
则1﹣m=﹣1,1+m=3,
故点(1﹣m,1+m)在第二象限.
故答案为:二.
16.【解答】解:∵函数y=3x+b和y=ax﹣3的图象交于点P(﹣2,﹣5),
∴不等式 3x+b>ax﹣3的解集是x>﹣2,
故答案为:x>﹣2.
17.【解答】解:设直线解析式为y=kx+b,
把(0,2)代入得b=2,
所以y=kx+2,
把y=0代入得x=-2k,
所以12×2×|-2k|=2,
解得:k=1或﹣1,
所以所求的直线解析式为y=x+2或y=﹣x+2.
故答案为:y=x+2或y=﹣x+2.
18.【解答】解:当x>1时,x+b>kx+4,
即不等式x+b>kx+4的解集为x>1.
故答案为x>1.
19.【解答】解:当x<﹣1时,k2x>k1x+b,
所以不等式k2x>k1x+b的解集为x<﹣1.
故答案为x<﹣1.
20.【解答】解:各边长减少xcm后,得到的新正方形的边长是3﹣xcm,
则周长y=4(3﹣x).
故答案是:y=4(3﹣x).
21.【解答】解:设此函数为一次函数,解析式为y=kx+b,
∵第二、四象限有它的图象,
∴k<0,可取﹣3,
∵在y轴上的截距为﹣2,
∴b=﹣2,
∴此函数解析式为y=﹣3x﹣2,
故答案为:y=﹣3x﹣2.
22.【解答】解:根据题意得:
①当0<x≤2.5时,y=6;
②当x>2.5时,y=6+1.3(x﹣2.5)=1.3x+2.75;
∴车费y(元)与路程x(千米)之间的函数关系式为:y=6(0<x≤2.5)1.3x+2.75(x>2.5),
故答案为:y=6(0<x≤2.5)1.3x+2.75(x>2.5).
23.【解答】解:因为一次函数y=12-23x中k=-23<0.
所以函数值y随x的增大而 减小.
故答案是;减小.
24.【解答】解:甲返程的速度为:600÷(14﹣6)=75,
设乙车的速度为x,
由题意得:600=7x+75,
解得:x=75,
故答案为75千米/小时.
25.【解答】解:∵直线y=kx+b与直线y=2x平行,
∴k=2,
∴y=2x+b,
把点A(1,2)代入y=2x+b得2+b=2,解得b=0;
∴k+b=2,
故答案为:2.
26.【解答】解:∵直线y=kx+b与x轴交于点(﹣2,0),
∴当y>0时,x的取值范围是x>﹣2,
故答案为:x>﹣2.
27.【解答】解:设所求一次函数解析式为y=﹣3x+b,
把(﹣1,0)代入得:0=3+b,
解得:b=﹣3,
则一次函数解析式为y=﹣3x﹣3,
故答案为:y=﹣3x﹣3.
