2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》解答题精选(Word版 含答案)
文档属性
| 名称 | 2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》解答题精选(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 197.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 14:32:20 | ||
图片预览

文档简介
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》解答题精选
一.解答题(共26小题)
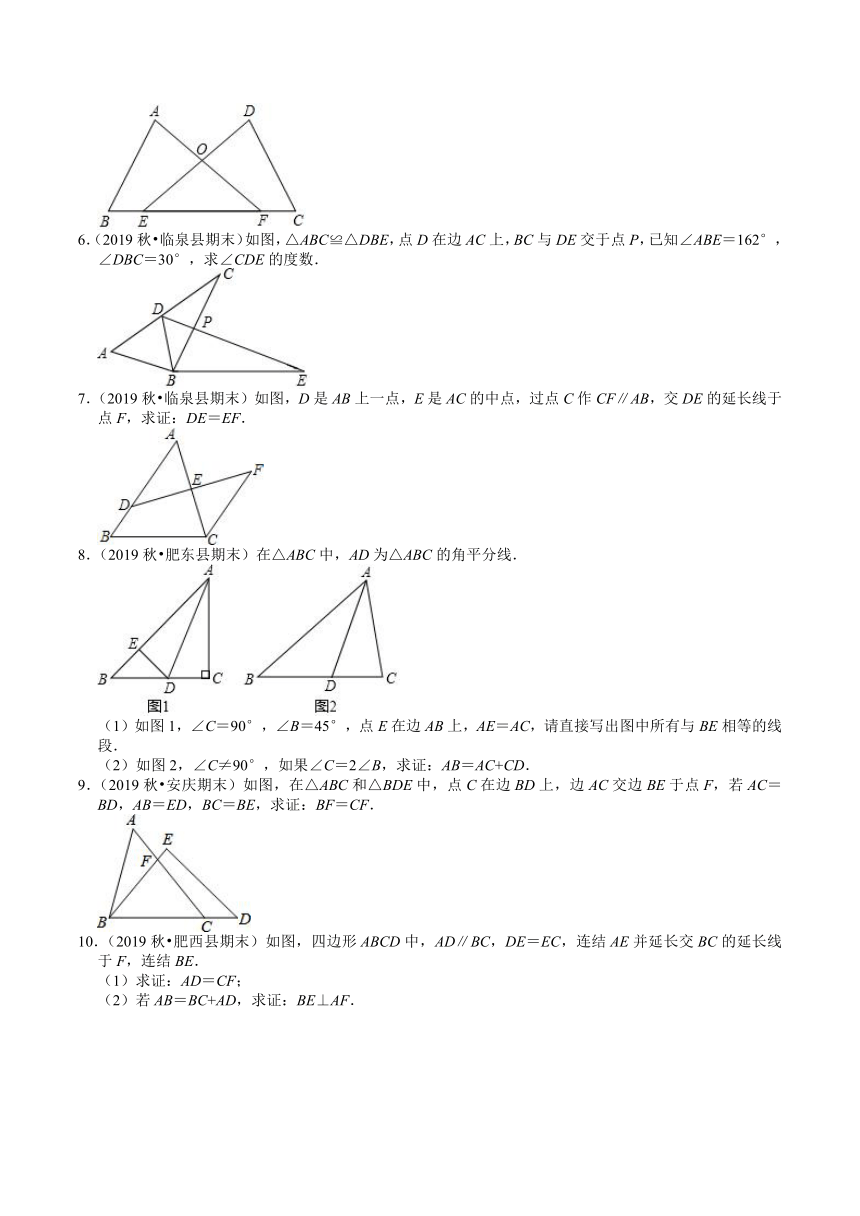
1.(2019秋?宿松县校级期末)如图,在△PAB中,PA=PB,∠APB=100°,点M,N,K分别是PA,PB,AB上的点,若MK=KN,∠MKN=40°,试判断线段AM,BN与AB之间的数量关系,并说明理由.
2.(2019秋?石台县期末)如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
(1)求证:△AEC≌△BED.
(2)若∠1=40°,求∠BDE的度数.
3.(2019秋?裕安区期末)如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
4.(2019秋?裕安区期末)如图,已知在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF.BE交FC于O点,
(1)求证:BE=CF;
(2)当∠BAC=70°时,求∠BOC的度数.
5.(2019秋?当涂县期末)如图,点E、F在BC上,AB=CD,BE=CF,AF=DE,AF与DE交于点O.
(1)求证:∠A=∠D;
(2)若∠EOF=90°,试判断△OEF的形状,并说明理由.
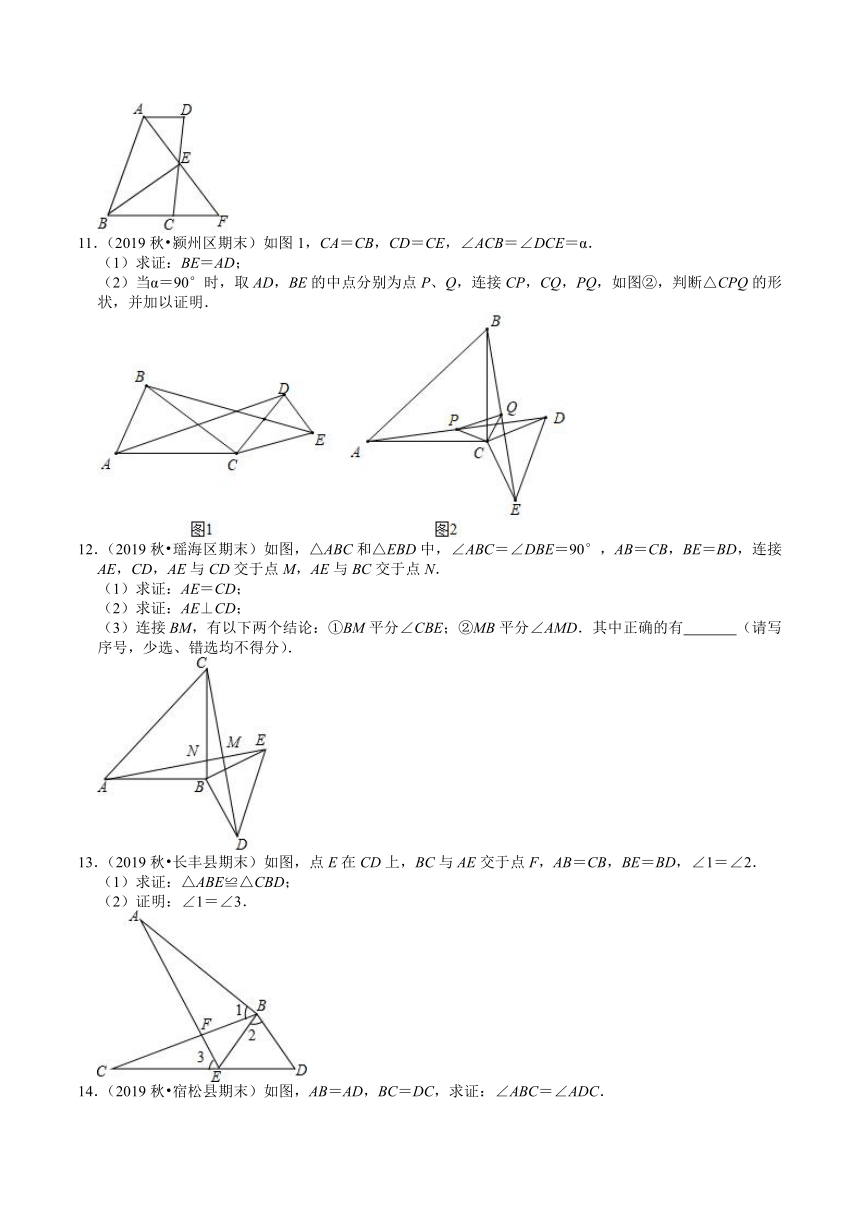
6.(2019秋?临泉县期末)如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
7.(2019秋?临泉县期末)如图,D是AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F,求证:DE=EF.
8.(2019秋?肥东县期末)在△ABC中,AD为△ABC的角平分线.
(1)如图1,∠C=90°,∠B=45°,点E在边AB上,AE=AC,请直接写出图中所有与BE相等的线段.
(2)如图2,∠C≠90°,如果∠C=2∠B,求证:AB=AC+CD.
9.(2019秋?安庆期末)如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,求证:BF=CF.
10.(2019秋?肥西县期末)如图,四边形ABCD中,AD∥BC,DE=EC,连结AE并延长交BC的延长线于F,连结BE.
(1)求证:AD=CF;
(2)若AB=BC+AD,求证:BE⊥AF.
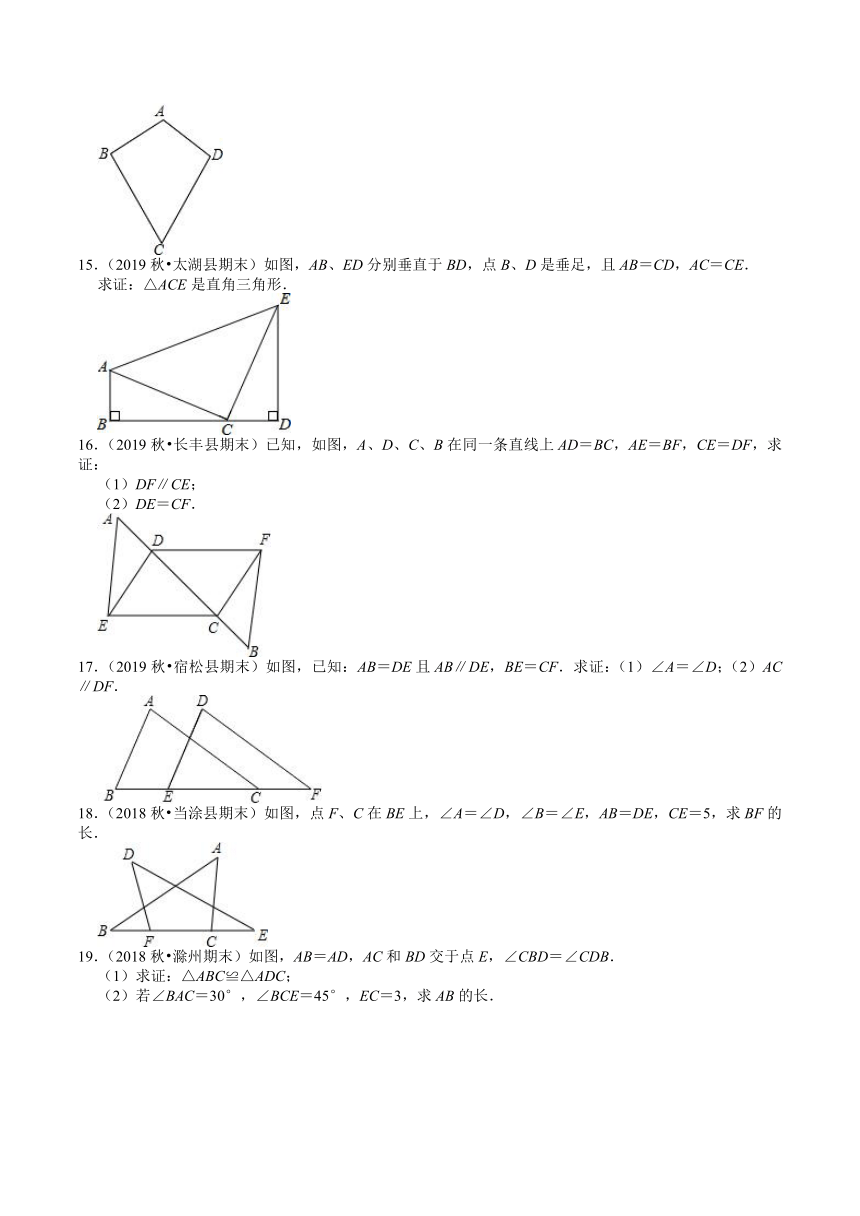
11.(2019秋?颍州区期末)如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
12.(2019秋?瑶海区期末)如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).
13.(2019秋?长丰县期末)如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
14.(2019秋?宿松县期末)如图,AB=AD,BC=DC,求证:∠ABC=∠ADC.
15.(2019秋?太湖县期末)如图,AB、ED分别垂直于BD,点B、D是垂足,且AB=CD,AC=CE.
求证:△ACE是直角三角形.
16.(2019秋?长丰县期末)已知,如图,A、D、C、B在同一条直线上AD=BC,AE=BF,CE=DF,求证:
(1)DF∥CE;
(2)DE=CF.
17.(2019秋?宿松县期末)如图,已知:AB=DE且AB∥DE,BE=CF.求证:(1)∠A=∠D;(2)AC∥DF.
18.(2018秋?当涂县期末)如图,点F、C在BE上,∠A=∠D,∠B=∠E,AB=DE,CE=5,求BF的长.
19.(2018秋?滁州期末)如图,AB=AD,AC和BD交于点E,∠CBD=∠CDB.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCE=45°,EC=3,求AB的长.
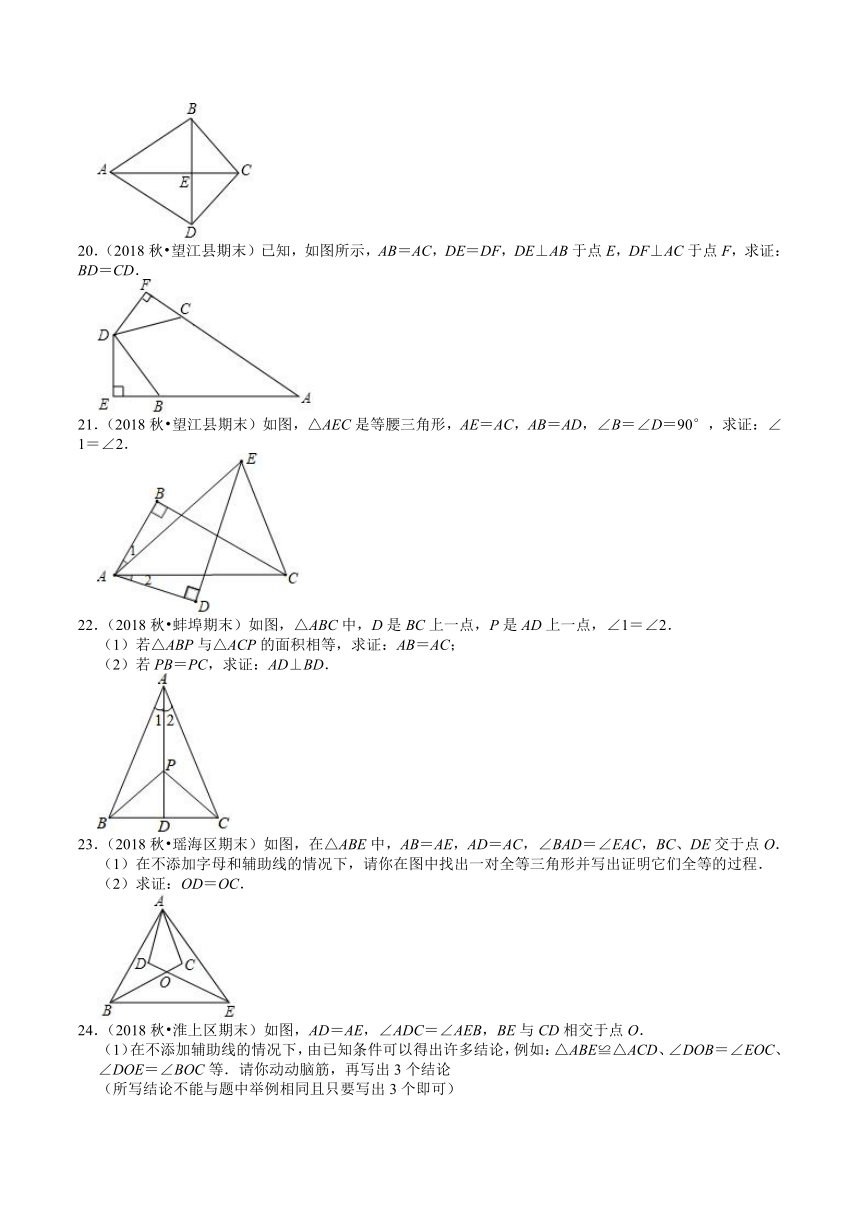
20.(2018秋?望江县期末)已知,如图所示,AB=AC,DE=DF,DE⊥AB于点E,DF⊥AC于点F,求证:BD=CD.
21.(2018秋?望江县期末)如图,△AEC是等腰三角形,AE=AC,AB=AD,∠B=∠D=90°,求证:∠1=∠2.
22.(2018秋?蚌埠期末)如图,△ABC中,D是BC上一点,P是AD上一点,∠1=∠2.
(1)若△ABP与△ACP的面积相等,求证:AB=AC;
(2)若PB=PC,求证:AD⊥BD.
23.(2018秋?瑶海区期末)如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.
(1)在不添加字母和辅助线的情况下,请你在图中找出一对全等三角形并写出证明它们全等的过程.
(2)求证:OD=OC.
24.(2018秋?淮上区期末)如图,AD=AE,∠ADC=∠AEB,BE与CD相交于点O.
(1)在不添加辅助线的情况下,由已知条件可以得出许多结论,例如:△ABE≌△ACD、∠DOB=∠EOC、∠DOE=∠BOC等.请你动动脑筋,再写出3个结论
(所写结论不能与题中举例相同且只要写出3个即可)
① ,② ,③ ;
(2)请你从自己写出的结论中,选取一个说明其成立的理由.
25.(2018秋?和县期末)把两个含有45°角的直角三角板DCE和ACB如图放置,点D在AC上,连接AE、BD.求证:BD⊥AE.
26.(2018秋?烈山区期末)已知:如图,AB,CD相交于点O,AC∥DB,OC=OD,E,F为AB上两点,且AE=BF.求证:CE∥DF.
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》解答题精选
参考答案与试题解析
一.解答题(共26小题)
1.【解答】解:AM+BN=AB,
理由如下:∵PA=PB,∠APB=100°,
∴∠A=∠B=40°,
∴∠AMK+∠AKM=140°,
∵∠MKN=40°,
∴∠AKM+∠BKN=140°,
∴∠AMK=∠BKN,
又∵MK=KN,
∴△AMK≌△BKN(AAS),
∴AM=BK,AK=BN,
∴AB=AK+BK=AM+BN.
2.【解答】(1)证明:∵∠1=∠2,
∴∠1+∠AED=∠2+∠AED,
∴∠AEC=∠BED,
在△AEC和△BED中
∠A=∠BAE=BE∠AEC=∠BED
∴△AEC≌△BED(ASA);
(2)∵△AEC≌△BED,
∴ED=EC,∠ACE=∠BDE,
∴∠ECD=∠EDC,
∵∠1=40°,
∴∠ECD=∠EDC=70°,
∴∠ECA=70°,
∴∠BDE=70°,
即∠BDE是70°.
3.【解答】解:∵△ACF≌△ADE,AD=12,AE=5,
∴AC=AD=12,AE=AF=5,
∴DF=12﹣5=7.
4.【解答】(1)证明:∵∠CAB=∠EAF,
∴∠CAB+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,
在△BAE和△CAF中
AB=AC∠BAE=∠CAFAE=AF
∴△BAE≌△CAF(SAS),
∴BE=CF;
(2)∵△BAE≌△CAF,
∴∠EBA=∠FCA,
即∠DBA=∠OCD,
∵∠BDA=∠ODC,
∴∠BAD=∠COD,
∵∠BAC=70°,
∴∠BAD=70°,
∴∠COD=70°,
即∠BOC=70°.
5.【解答】(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中AB=DCAF=DEBF=CE
∴△ABF≌△DCE(SSS),
∴∠A=∠D;
(2)△OEF是等腰直角三角形,
∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∵∠EOF=90°,
∴△OEF是等腰直角三角形.
6.【解答】解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
7.【解答】解:∵点E是AC中点,
∴AE=EC,
∵CF∥AB,
∴∠A=∠ECF,且AE=EC,∠AED=∠CEF,
∴△AED≌△CEF(SAS)
∴DE=EF.
8.【解答】解:(1)与BE相等的线段是DE和DC,
理由:∵AD为△ABC的角平分线,
∴∠CAD=∠EAD,
在△AED和△ACD中
AE=AC∠EAD=∠CADAD=AD
∴△AED≌△ACD(SAS),
∴DE=DC,∠DEA=∠C=90°,
∴∠DEB=90°,
∵∠B=45°,
∴∠B=∠BDE,
∴BE=DE,
∴BE=DE=DC,
即与BE相等的线段是DE和DC;
(2)在AB上截取AE=AC,连接DE,
∵AD为△ABC的角平分线,
∴∠CAD=∠EAD,
在在△AED和△ACD中
AE=AC∠EAD=∠CADAD=AD
∴△AED≌△ACD(SAS),
∴∠C=∠AED,CD=ED,
∵∠C=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴ED=EB,
∴EB=CD,
∵AB=AE+EB,
∴AB=AC+CD.
9.【解答】证明:在△ABC与△DEB中,
AC=BDAB=EDBC=BE,
∴△ABC≌△DEB(SSS)
∴∠ACB=∠EBD,
∴BF=CF.
10.【解答】解:(1)证明:∵AD∥BC,
∴∠DAE=∠F,∠ADE=∠FCE.
∵点E是DC的中点,
∴DE=CE.
在△ADE和△FCE中
∠DAF=∠F∠ADE=∠FCEDE=CE,
∴△ADE≌△FCE(AAS),
∴CF=AD.
(2)∵CF=AD,AB=BC+AD,
∴AB=BF,
∵△ADE≌△FCE,
∴AE=EF,
∴BE⊥AF.
11.【解答】解:(1)如图1,
∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
CA=CB∠ACD=∠BCECD=CE,
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)△CPQ为等腰直角三角形.
证明:如图2,
由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
CA=CB∠CAP=∠CBQAP=BQ,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形
12.【解答】(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
AB=CB∠ABE=∠CBDBE=BD,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,
又∠CNM=∠ANB,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴12?AE?BK=12?CD?BJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.
故答案为②.
13.【解答】证明:(1)∵∠1=∠2,
∴∠1+∠CBE=∠2+∠CBE,即∠ABE=∠CBD,
在△ABE和△CBD中,
AB=CB∠ABE=∠CBDBE=BD,
∴△ABE≌△CBD(SAS);
(2)∵△ABE≌△CBD,
∴∠A=∠C,
∵∠AFB=∠CFE,
∴∠1=∠3.
14.【解答】证明:连接AC,
在△ABC与△ADC中,
AB=ADBC=DCAC=AC,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC.
15.【解答】证明:∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,
在Rt△ABC和Rt△CDE中
AB=CDAC=CE,
∴Rt△ABC≌Rt△CDE(HL),
∴∠1=∠3,
∵∠2+∠3=90°,
∴∠1+∠2=90°,
∴∠ACE=90°,
∴△ACE是直角三角形.
16.【解答】证明:(1)∵AD=BC,∴AC=BD,
又AE=BF,CE=DF,
∴△ACE≌△BDF(SSS)
∴∠FDC=∠ECD,
∴DF∥CE;
(2)由(1)可得∠A=∠B,
AD=BC,AE=BF,
∴△ADE≌△BCF(SAS),∴DE=CF
17.【解答】证明:(1)∵AB∥DE,BE=CF,
∴∠B=∠DEF,BC=EF,
又AB=DE,
∴△ABC≌△DEF(SAS),
∴∠A=∠D;
(2)由(1)知△ABC≌△DEF,
∴∠ACB=∠F,
∴AC∥DF.
18.【解答】解:在△ABC和△DEF中,
∠A=∠DAB=DE∠B=∠E,
∴△ABC≌△DEF(ASA),
∴BC=EF.
∴CE=BF,
∵CE=5,
∴BF=5.
19.【解答】(1)证明:∵∠CBD=∠CDB,
∴BC=DC,
在△ABC和△ADC中,AB=ADBC=DCAC=AC,
∴△ABC≌△ADC(SSS);
(2)解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AB=AD,
∴AC⊥BD,
在Rt△BCE中,∠BCE=45°,
∴EC=BE=3,
在Rt△ABE中,∠BAC=30°,
∴AB=2BE=2×3=6.
20.【解答】证明:连接AD,
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠F=∠E=90°,
∵DE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL)
∴AE=AF,且AB=AC,
∴EB=FC,且∠F=∠E=90°,DE=DF,
∴△DEB≌△DFC(SAS)
∴DB=DC.
21.【解答】证明:∵AE=AC,且AB=AD,∠B=∠D=90°,
∴Rt△ABC≌Rt△ADE(HL)
∴∠BAC=∠DAE,
∴∠1=∠2.
22.【解答】(1)证明:如图,作PM⊥AB于M,PN⊥AC于N.
∵∠1=∠2,PM⊥AB于M,PN⊥AC于N,
∴PM=PN,
∵S△PAB=S△PAC,
∴12?AB?PM=12?AC?PN,
∴AB=AC.
(2)证明:在Rt△PBM和Rt△PCN中,
PB=PCPM=PN,
∴Rt△PBM≌Rt△PCN(HL),
∴∠PBM=∠PCN,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠ABC=∠ACB,
∴AB=AC,
∵∠1=∠2,
∴AD⊥BC.
23.【解答】解:(1)全等三角形为:△ABC≌△AED
理由如下:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC
即∠BAC=∠EAD,且AB=AE,AC=AD
∴△ABC≌△AED(SAS)
(2)由(1)知△ABC≌△AED
∴∠ABC=∠AED,BC=DE
∵AB=AE
∴∠ABE=∠AEB,
∴∠ABE﹣∠ABC=∠AEB﹣∠AED
∴∠OBE=∠0EB
∴OB=OE
∴BC﹣OB=DE﹣OE
∴OD=OC
24.【解答】解:(1)①△DBC≌△ECB;②∠ACD=∠ABE;③BD=CE;
故答案为△DBC≌△ECB
(2)选择③BD=CE.
理由:在△ABE与△ACD中
∠A=∠A,AD=AE,∠ADC=∠AEB,
∴△ABE≌△ACD(ASA),
∴AB=AC,
∴AB﹣AD=AC﹣AE,
∴BD=CE.
25.【解答】证明:延长BD交AE于F,
在△AEC和△BDC中,
EC=CD∠ECA=∠BCD=90°AC=CB,
∴△AEC≌△BDC(SAS),
∴∠DBC=∠EAC,
∵∠BDC=∠ADF
∴∠DCB=∠DFA=90°,
∴BD⊥AE.
26.【解答】证明:∵AC∥BD,
∴∠A=∠B,
在△ACO和△BDO中
∠AOC=∠BOD∠A=∠BOC=OD
∴△ACO≌△BDO
∴OA=OB,
∵AE=BF,
∴OE=OF,
在△COE和△DOF中
OC=OD∠COE=∠DOFOE=OF
∴△COE≌△DOF,
∴∠OEC=∠OFD,
∴CE∥DF.
一.解答题(共26小题)
1.(2019秋?宿松县校级期末)如图,在△PAB中,PA=PB,∠APB=100°,点M,N,K分别是PA,PB,AB上的点,若MK=KN,∠MKN=40°,试判断线段AM,BN与AB之间的数量关系,并说明理由.
2.(2019秋?石台县期末)如图,∠A=∠B,AE=BE,∠1=∠2,点D在AC边上.
(1)求证:△AEC≌△BED.
(2)若∠1=40°,求∠BDE的度数.
3.(2019秋?裕安区期末)如图,△ACF≌△ADE,AD=12,AE=5,求DF的长.
4.(2019秋?裕安区期末)如图,已知在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF.BE交FC于O点,
(1)求证:BE=CF;
(2)当∠BAC=70°时,求∠BOC的度数.
5.(2019秋?当涂县期末)如图,点E、F在BC上,AB=CD,BE=CF,AF=DE,AF与DE交于点O.
(1)求证:∠A=∠D;
(2)若∠EOF=90°,试判断△OEF的形状,并说明理由.
6.(2019秋?临泉县期末)如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,求∠CDE的度数.
7.(2019秋?临泉县期末)如图,D是AB上一点,E是AC的中点,过点C作CF∥AB,交DE的延长线于点F,求证:DE=EF.
8.(2019秋?肥东县期末)在△ABC中,AD为△ABC的角平分线.
(1)如图1,∠C=90°,∠B=45°,点E在边AB上,AE=AC,请直接写出图中所有与BE相等的线段.
(2)如图2,∠C≠90°,如果∠C=2∠B,求证:AB=AC+CD.
9.(2019秋?安庆期末)如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F,若AC=BD,AB=ED,BC=BE,求证:BF=CF.
10.(2019秋?肥西县期末)如图,四边形ABCD中,AD∥BC,DE=EC,连结AE并延长交BC的延长线于F,连结BE.
(1)求证:AD=CF;
(2)若AB=BC+AD,求证:BE⊥AF.
11.(2019秋?颍州区期末)如图1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求证:BE=AD;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
12.(2019秋?瑶海区期末)如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有 (请写序号,少选、错选均不得分).
13.(2019秋?长丰县期末)如图,点E在CD上,BC与AE交于点F,AB=CB,BE=BD,∠1=∠2.
(1)求证:△ABE≌△CBD;
(2)证明:∠1=∠3.
14.(2019秋?宿松县期末)如图,AB=AD,BC=DC,求证:∠ABC=∠ADC.
15.(2019秋?太湖县期末)如图,AB、ED分别垂直于BD,点B、D是垂足,且AB=CD,AC=CE.
求证:△ACE是直角三角形.
16.(2019秋?长丰县期末)已知,如图,A、D、C、B在同一条直线上AD=BC,AE=BF,CE=DF,求证:
(1)DF∥CE;
(2)DE=CF.
17.(2019秋?宿松县期末)如图,已知:AB=DE且AB∥DE,BE=CF.求证:(1)∠A=∠D;(2)AC∥DF.
18.(2018秋?当涂县期末)如图,点F、C在BE上,∠A=∠D,∠B=∠E,AB=DE,CE=5,求BF的长.
19.(2018秋?滁州期末)如图,AB=AD,AC和BD交于点E,∠CBD=∠CDB.
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCE=45°,EC=3,求AB的长.
20.(2018秋?望江县期末)已知,如图所示,AB=AC,DE=DF,DE⊥AB于点E,DF⊥AC于点F,求证:BD=CD.
21.(2018秋?望江县期末)如图,△AEC是等腰三角形,AE=AC,AB=AD,∠B=∠D=90°,求证:∠1=∠2.
22.(2018秋?蚌埠期末)如图,△ABC中,D是BC上一点,P是AD上一点,∠1=∠2.
(1)若△ABP与△ACP的面积相等,求证:AB=AC;
(2)若PB=PC,求证:AD⊥BD.
23.(2018秋?瑶海区期末)如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC,BC、DE交于点O.
(1)在不添加字母和辅助线的情况下,请你在图中找出一对全等三角形并写出证明它们全等的过程.
(2)求证:OD=OC.
24.(2018秋?淮上区期末)如图,AD=AE,∠ADC=∠AEB,BE与CD相交于点O.
(1)在不添加辅助线的情况下,由已知条件可以得出许多结论,例如:△ABE≌△ACD、∠DOB=∠EOC、∠DOE=∠BOC等.请你动动脑筋,再写出3个结论
(所写结论不能与题中举例相同且只要写出3个即可)
① ,② ,③ ;
(2)请你从自己写出的结论中,选取一个说明其成立的理由.
25.(2018秋?和县期末)把两个含有45°角的直角三角板DCE和ACB如图放置,点D在AC上,连接AE、BD.求证:BD⊥AE.
26.(2018秋?烈山区期末)已知:如图,AB,CD相交于点O,AC∥DB,OC=OD,E,F为AB上两点,且AE=BF.求证:CE∥DF.
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》解答题精选
参考答案与试题解析
一.解答题(共26小题)
1.【解答】解:AM+BN=AB,
理由如下:∵PA=PB,∠APB=100°,
∴∠A=∠B=40°,
∴∠AMK+∠AKM=140°,
∵∠MKN=40°,
∴∠AKM+∠BKN=140°,
∴∠AMK=∠BKN,
又∵MK=KN,
∴△AMK≌△BKN(AAS),
∴AM=BK,AK=BN,
∴AB=AK+BK=AM+BN.
2.【解答】(1)证明:∵∠1=∠2,
∴∠1+∠AED=∠2+∠AED,
∴∠AEC=∠BED,
在△AEC和△BED中
∠A=∠BAE=BE∠AEC=∠BED
∴△AEC≌△BED(ASA);
(2)∵△AEC≌△BED,
∴ED=EC,∠ACE=∠BDE,
∴∠ECD=∠EDC,
∵∠1=40°,
∴∠ECD=∠EDC=70°,
∴∠ECA=70°,
∴∠BDE=70°,
即∠BDE是70°.
3.【解答】解:∵△ACF≌△ADE,AD=12,AE=5,
∴AC=AD=12,AE=AF=5,
∴DF=12﹣5=7.
4.【解答】(1)证明:∵∠CAB=∠EAF,
∴∠CAB+∠CAE=∠EAF+∠CAE,
∴∠BAE=∠CAF,
在△BAE和△CAF中
AB=AC∠BAE=∠CAFAE=AF
∴△BAE≌△CAF(SAS),
∴BE=CF;
(2)∵△BAE≌△CAF,
∴∠EBA=∠FCA,
即∠DBA=∠OCD,
∵∠BDA=∠ODC,
∴∠BAD=∠COD,
∵∠BAC=70°,
∴∠BAD=70°,
∴∠COD=70°,
即∠BOC=70°.
5.【解答】(1)证明:∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△ABF和△DCE中AB=DCAF=DEBF=CE
∴△ABF≌△DCE(SSS),
∴∠A=∠D;
(2)△OEF是等腰直角三角形,
∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∴OE=OF,
∵∠EOF=90°,
∴△OEF是等腰直角三角形.
6.【解答】解:∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,∠C=∠E,
∴∠ABD=∠CBE=132°÷2=66°,
∵∠CPD=∠BPE,
∴∠CDE=∠CBE=66°.
7.【解答】解:∵点E是AC中点,
∴AE=EC,
∵CF∥AB,
∴∠A=∠ECF,且AE=EC,∠AED=∠CEF,
∴△AED≌△CEF(SAS)
∴DE=EF.
8.【解答】解:(1)与BE相等的线段是DE和DC,
理由:∵AD为△ABC的角平分线,
∴∠CAD=∠EAD,
在△AED和△ACD中
AE=AC∠EAD=∠CADAD=AD
∴△AED≌△ACD(SAS),
∴DE=DC,∠DEA=∠C=90°,
∴∠DEB=90°,
∵∠B=45°,
∴∠B=∠BDE,
∴BE=DE,
∴BE=DE=DC,
即与BE相等的线段是DE和DC;
(2)在AB上截取AE=AC,连接DE,
∵AD为△ABC的角平分线,
∴∠CAD=∠EAD,
在在△AED和△ACD中
AE=AC∠EAD=∠CADAD=AD
∴△AED≌△ACD(SAS),
∴∠C=∠AED,CD=ED,
∵∠C=2∠B,
∴∠AED=2∠B,
∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴ED=EB,
∴EB=CD,
∵AB=AE+EB,
∴AB=AC+CD.
9.【解答】证明:在△ABC与△DEB中,
AC=BDAB=EDBC=BE,
∴△ABC≌△DEB(SSS)
∴∠ACB=∠EBD,
∴BF=CF.
10.【解答】解:(1)证明:∵AD∥BC,
∴∠DAE=∠F,∠ADE=∠FCE.
∵点E是DC的中点,
∴DE=CE.
在△ADE和△FCE中
∠DAF=∠F∠ADE=∠FCEDE=CE,
∴△ADE≌△FCE(AAS),
∴CF=AD.
(2)∵CF=AD,AB=BC+AD,
∴AB=BF,
∵△ADE≌△FCE,
∴AE=EF,
∴BE⊥AF.
11.【解答】解:(1)如图1,
∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
CA=CB∠ACD=∠BCECD=CE,
∴△ACD≌△BCE(SAS),
∴BE=AD;
(2)△CPQ为等腰直角三角形.
证明:如图2,
由(1)可得,BE=AD,
∵AD,BE的中点分别为点P、Q,
∴AP=BQ,
∵△ACD≌△BCE,
∴∠CAP=∠CBQ,
在△ACP和△BCQ中,
CA=CB∠CAP=∠CBQAP=BQ,
∴△ACP≌△BCQ(SAS),
∴CP=CQ,且∠ACP=∠BCQ,
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形
12.【解答】(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
AB=CB∠ABE=∠CBDBE=BD,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,
又∠CNM=∠ANB,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴12?AE?BK=12?CD?BJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.
故答案为②.
13.【解答】证明:(1)∵∠1=∠2,
∴∠1+∠CBE=∠2+∠CBE,即∠ABE=∠CBD,
在△ABE和△CBD中,
AB=CB∠ABE=∠CBDBE=BD,
∴△ABE≌△CBD(SAS);
(2)∵△ABE≌△CBD,
∴∠A=∠C,
∵∠AFB=∠CFE,
∴∠1=∠3.
14.【解答】证明:连接AC,
在△ABC与△ADC中,
AB=ADBC=DCAC=AC,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC.
15.【解答】证明:∵AB⊥BD,ED⊥BD,
∴∠B=∠D=90°,
在Rt△ABC和Rt△CDE中
AB=CDAC=CE,
∴Rt△ABC≌Rt△CDE(HL),
∴∠1=∠3,
∵∠2+∠3=90°,
∴∠1+∠2=90°,
∴∠ACE=90°,
∴△ACE是直角三角形.
16.【解答】证明:(1)∵AD=BC,∴AC=BD,
又AE=BF,CE=DF,
∴△ACE≌△BDF(SSS)
∴∠FDC=∠ECD,
∴DF∥CE;
(2)由(1)可得∠A=∠B,
AD=BC,AE=BF,
∴△ADE≌△BCF(SAS),∴DE=CF
17.【解答】证明:(1)∵AB∥DE,BE=CF,
∴∠B=∠DEF,BC=EF,
又AB=DE,
∴△ABC≌△DEF(SAS),
∴∠A=∠D;
(2)由(1)知△ABC≌△DEF,
∴∠ACB=∠F,
∴AC∥DF.
18.【解答】解:在△ABC和△DEF中,
∠A=∠DAB=DE∠B=∠E,
∴△ABC≌△DEF(ASA),
∴BC=EF.
∴CE=BF,
∵CE=5,
∴BF=5.
19.【解答】(1)证明:∵∠CBD=∠CDB,
∴BC=DC,
在△ABC和△ADC中,AB=ADBC=DCAC=AC,
∴△ABC≌△ADC(SSS);
(2)解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,
∵AB=AD,
∴AC⊥BD,
在Rt△BCE中,∠BCE=45°,
∴EC=BE=3,
在Rt△ABE中,∠BAC=30°,
∴AB=2BE=2×3=6.
20.【解答】证明:连接AD,
∵DE⊥AB于点E,DF⊥AC于点F,
∴∠F=∠E=90°,
∵DE=DF,AD=AD,
∴Rt△ADE≌Rt△ADF(HL)
∴AE=AF,且AB=AC,
∴EB=FC,且∠F=∠E=90°,DE=DF,
∴△DEB≌△DFC(SAS)
∴DB=DC.
21.【解答】证明:∵AE=AC,且AB=AD,∠B=∠D=90°,
∴Rt△ABC≌Rt△ADE(HL)
∴∠BAC=∠DAE,
∴∠1=∠2.
22.【解答】(1)证明:如图,作PM⊥AB于M,PN⊥AC于N.
∵∠1=∠2,PM⊥AB于M,PN⊥AC于N,
∴PM=PN,
∵S△PAB=S△PAC,
∴12?AB?PM=12?AC?PN,
∴AB=AC.
(2)证明:在Rt△PBM和Rt△PCN中,
PB=PCPM=PN,
∴Rt△PBM≌Rt△PCN(HL),
∴∠PBM=∠PCN,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠ABC=∠ACB,
∴AB=AC,
∵∠1=∠2,
∴AD⊥BC.
23.【解答】解:(1)全等三角形为:△ABC≌△AED
理由如下:∵∠BAD=∠EAC,
∴∠BAD+∠DAC=∠EAC+∠DAC
即∠BAC=∠EAD,且AB=AE,AC=AD
∴△ABC≌△AED(SAS)
(2)由(1)知△ABC≌△AED
∴∠ABC=∠AED,BC=DE
∵AB=AE
∴∠ABE=∠AEB,
∴∠ABE﹣∠ABC=∠AEB﹣∠AED
∴∠OBE=∠0EB
∴OB=OE
∴BC﹣OB=DE﹣OE
∴OD=OC
24.【解答】解:(1)①△DBC≌△ECB;②∠ACD=∠ABE;③BD=CE;
故答案为△DBC≌△ECB
(2)选择③BD=CE.
理由:在△ABE与△ACD中
∠A=∠A,AD=AE,∠ADC=∠AEB,
∴△ABE≌△ACD(ASA),
∴AB=AC,
∴AB﹣AD=AC﹣AE,
∴BD=CE.
25.【解答】证明:延长BD交AE于F,
在△AEC和△BDC中,
EC=CD∠ECA=∠BCD=90°AC=CB,
∴△AEC≌△BDC(SAS),
∴∠DBC=∠EAC,
∵∠BDC=∠ADF
∴∠DCB=∠DFA=90°,
∴BD⊥AE.
26.【解答】证明:∵AC∥BD,
∴∠A=∠B,
在△ACO和△BDO中
∠AOC=∠BOD∠A=∠BOC=OD
∴△ACO≌△BDO
∴OA=OB,
∵AE=BF,
∴OE=OF,
在△COE和△DOF中
OC=OD∠COE=∠DOFOE=OF
∴△COE≌△DOF,
∴∠OEC=∠OFD,
∴CE∥DF.
