2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章全等三角形选择题精选(Word版含答案)
文档属性
| 名称 | 2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章全等三角形选择题精选(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 172.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览

文档简介
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》选择题精选
一.选择题(共36小题)
1.(2019秋?宿松县校级期末)在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )
A.3个 B.4个 C.6个 D.7个
2.(2019秋?石台县期末)已知图中的两个三角形全等,则∠1等于( )
A.70° B.50° C.60° D.120°
3.(2019秋?蜀山区期末)如图,∠BDA=∠BDC,现添加以下哪个条件不能判定△ABD≌△CBD的是( )
A.∠A=∠C B.∠ABD=∠CBD C.AB=CB D.AD=CD
4.(2019秋?蜀山区期末)如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
5.(2019秋?蜀山区期末)如图,△ABC≌△DEC,点E在边AB上,∠DEC=75°,则∠BCE的度数是( )
A.25° B.30° C.40° D.75°
6.(2019秋?肥东县期末)已知△ABC如图所示,另有△DEF,满足ED=AB,DF=AC,∠E=∠B.下列结论一定正确的是( )
A.BC=EF
B.∠C=∠F
C.△ABC中BC边上的高=△DEF中EF边上的高
D.△ABC中BC边上的中线=△DEF中EF边上的中线
7.(2019秋?肥东县期末)如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性这样做的道理是( )
A.两点之间的所有连线中线段最短
B.三角形具有稳定性
C.经过两点有一条直线,并且只有一条直线拉杆
D.在连接直线外一点与直线上各点的线段中,垂线段最短
8.(2019秋?谢家集区期末)如图,已知AB=DE,∠1=∠2.若要得到△ABC≌△DEF,则下列条件中不符合要求的是( )
A.∠A=∠D B.∠C=∠F C.AC=DF D.CE=FB
9.(2019秋?肥东县期末)如图,△ABC≌△DBE,点D在线段AC上,线段BC与DE交于点F下面各项中,不能推导出的结论是( )
A.∠EBF=∠ABD B.∠EBF=∠FDC C.∠ABD=∠FDC D.∠ABD=∠FBD
10.(2019秋?包河区期末)如图所示,在△ABC和△DEF中,AB=DE,∠A=∠D,若证△ABC≌△DEF还要从下列条件中补选一个,错误的选法是( )
A.∠ABC=∠DEF B.∠ACB=∠DFE C.AC=DF D.BC=EF
11.(2019秋?无为县期末)如图,AC与BD相交于点O,∠DAB=∠CBA,添加下列哪一个条件后,仍不能使△ADB≌△CBA的是( )
A.AD=BC B.∠ABD=∠BAC C.OA=OB D.AC=BD
12.(2019秋?瑶海区期末)如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F.若AB=DE,BC=BE,AC=BD,则∠ACB等于( )
A.∠D B.∠E C.2∠ABF D.12∠AFB
13.(2019秋?当涂县期末)如图,已知∠1=∠2,下列添加的条件不能使△ADC≌△CBA的是( )
A.AB∥DC B.AB=CD C.AD=BC D.∠B=∠D
14.(2019秋?义安区期末)如图,已知AB=DE,BE=CF,添加下列条件中哪一个能使△ABC≌△DEF( )
A.∠A=∠D B.AB∥DE C.BE=EC D.AC∥DF
15.(2019秋?田家庵区期末)如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为( )
A.3 B.4 C.5 D.6
16.(2019秋?全椒县期末)如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
17.(2019秋?蚌埠期末)如图、点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
18.(2019秋?裕安区期末)如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF,下列条件不能判定△ABC≌△DEF的是( )
A.AD=CF B.∠BCA=∠F C.∠B=∠E D.BC=EF
19.(2019秋?裕安区期末)如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A,C两点之间 B.G,H两点之间
C.B,F两点之间 D.E,G两点之间
20.(2019秋?颍州区期末)如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
A.BF=EC B.AC=DF C.∠B=∠E D.BF=FC
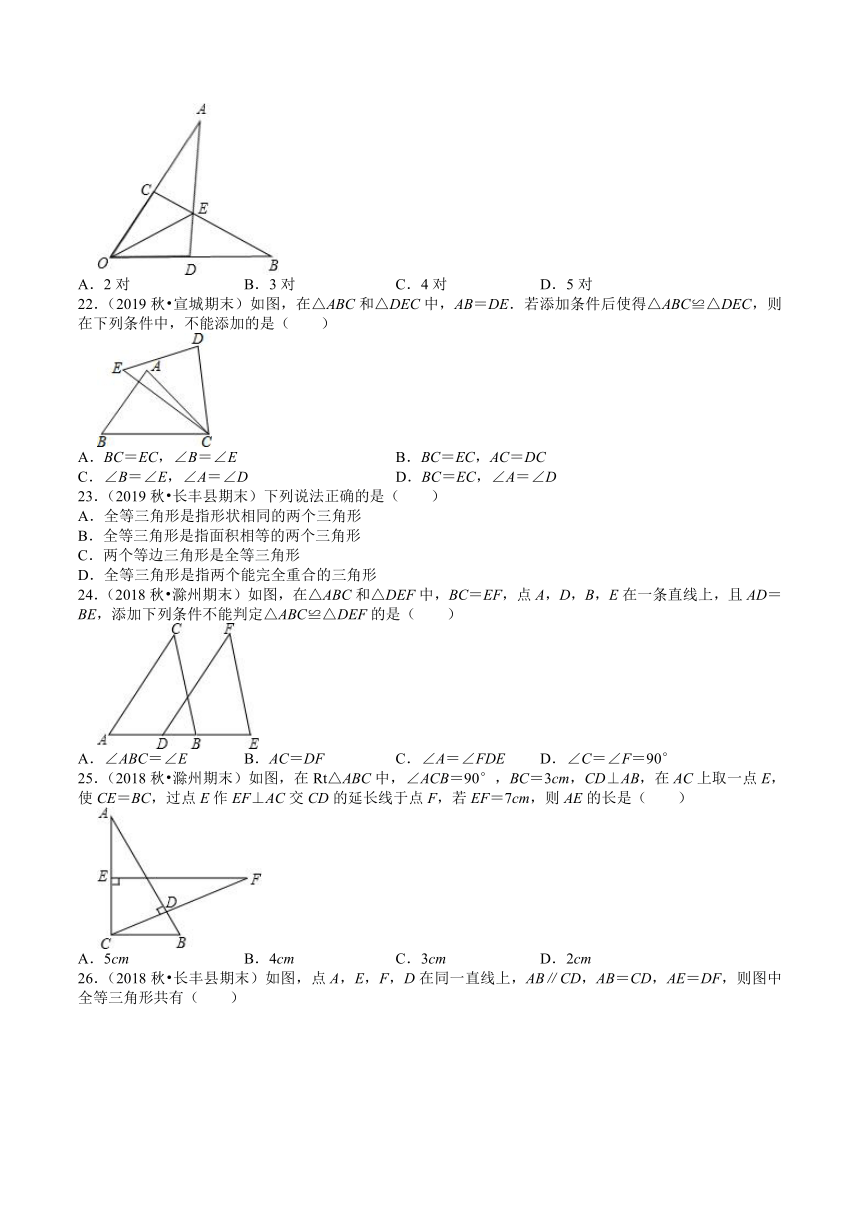
21.(2019秋?太湖县期末)如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )
A.2对 B.3对 C.4对 D.5对
22.(2019秋?宣城期末)如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D D.BC=EC,∠A=∠D
23.(2019秋?长丰县期末)下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.两个等边三角形是全等三角形
D.全等三角形是指两个能完全重合的三角形
24.(2018秋?滁州期末)如图,在△ABC和△DEF中,BC=EF,点A,D,B,E在一条直线上,且AD=BE,添加下列条件不能判定△ABC≌△DEF的是( )
A.∠ABC=∠E B.AC=DF C.∠A=∠FDE D.∠C=∠F=90°
25.(2018秋?滁州期末)如图,在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,在AC上取一点E,使CE=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE的长是( )
A.5cm B.4cm C.3cm D.2cm
26.(2018秋?长丰县期末)如图,点A,E,F,D在同一直线上,AB∥CD,AB=CD,AE=DF,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
27.(2018秋?蜀山区期末)如图,△ABC≌△ADC,AC、BD相交于点O,下列结论不一定正确的是( )
A.AC平分∠BAD B.AC平分∠BCD C.AC平分BD D.BD平分AC
28.(2018秋?颍上县期末)如图,在△ABC中,AC⊥BC,AE为∠BAC的平分线,ED⊥AB于点D,AB=7cm,AC=3cm,则BD的长为( )
A.3cm B.4cm C.1cm D.2cm
29.(2018秋?无为县期末)下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
30.(2018秋?阜南县期末)如图,下列条件中,不能证明△ABC≌△DCB的条件是( )
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.AB=DC,∠DBC=∠ACB D.∠DBC=∠ACB,∠A=∠D
31.(2018秋?宣城期末)如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4 B.6 C.4或9 D.6或9
32.(2018秋?寿县期末)已知图中的两个三角形全等,则∠1等于( )
A.50° B.58° C.60° D.72°
33.(2018秋?太湖县期末)下列条件,不能判定两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.两个锐角对应相等
C.一锐角和斜边对应相等
D.两条直角边对应相等
34.(2017秋?濉溪县期末)如图,AD=AE,BE=CD,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE C.∠DAE=40° D.∠C=30°
35.(2017秋?蜀山区期末)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )
A.71° B.76° C.78° D.80°
36.(2017秋?望江县期末)若△ABC≌△MNP,∠A=∠M,∠C=∠P,AB=4cm,BC=2cm,则NP=( )
A.2cm B.3cm C.4cm D.6cm
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》选择题精选
参考答案与试题解析
一.选择题(共36小题)
1.【解答】解:如图所示:一共有7个符合题意的点.
故选:D.
2.【解答】解:∵△ABC≌△DEF,
∴∠E=∠B=70°,
∴∠1=180°﹣50°﹣70°=60°,
故选:C.
3.【解答】解:∵∠BDA=∠BDC,BD=BD,
∴当添加∠A=∠C时,可根据“AAS”判断△ABD≌△CBD;
当添加∠ABD=∠CBD时,可根据“ASA”判断△ABD≌△CBD;
当添加AD=CD时,可根据“SAS”判断△ABD≌△CBD.
故选:C.
4.【解答】证明:∵FC∥AB
∴∠FCE=∠DAE,
在△CFE和△ADE中
∠FCE=∠DAECE=AE∠CEF=∠AED,
∴△CFE≌△ADE(ASA),
∴AD=CF=5,
∵AB=3,
∴BD=5﹣3=2,
故选:D.
5.【解答】解:∵△ABC≌△DEC,
∴∠B=∠DEC=75°,CE=CB,
∴∠CEB=∠B=75°,∠B=∠CEB,
∴∠BCE=180°﹣2×75°=30°,
故选:B.
6.【解答】解:如图,过点A作AH⊥BC于H,过点D作DG⊥EF于G,
∵AB=DE,∠B=∠E,∠AHB=∠DGE,
∴△ABH≌△DEG(AAS)
∴AH=DG,
∴△ABC中BC边上的高=△DEF中EF边上的高,
故选:C.
7.【解答】解:人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性这样做的道理是三角形具有稳定性,
故选:B.
8.【解答】解:A、添加∠A=∠D,根据ASA可以判定△ABC≌△DEF,故本选项不符合题意.
B、添加∠C=∠F,根据AAS可以判定△ABC≌△DEF,故本选项不符合题意.
C、添加AC=DF,根据SSA不可以判定△ABC≌△DEF,故本选项符合题意.
D、添加CE=FB可以得到BC=EF,根据SAS可以判定△ABC≌△DEF,故本选项不符合题意.
故选:C.
9.【解答】解:∵△ABC≌△DBE,
∴∠EBD=∠CBA,∠A=∠BDE,
∴∠EBF=∠ABD,故A不合题意;
∵AB=BD,
∴∠A=∠BDF=∠BDE,
∴∠A+∠ADB=∠ADB+∠BDE,
∴∠EBF=∠FDC=∠EBF,故B,C不合题意;
无法得出∠ABD=∠FBD,故此选项符合题意.
故选:D.
10.【解答】解:∵AB=DE,∠A=∠D,∠ABC=∠DEF,
∴△ABC≌△DEF(ASA),
故A选项不符合题意;
∵AB=DE,∠A=∠D,∠ACB=∠DFE,
∴△ABC≌△DEF(AAS),
故B选项不符合题意;
∵AB=DE,∠A=∠D,AC=DF,
∴△ABC≌△DEF(SAS),
故C选项不符合题意;
∵AB=DE,∠A=∠D,BC=EF,
无法证明△ABC与△DEF全等,
故D选项符合题意;
故选:D.
11.【解答】解:∵∠DAB=∠CBA,AB=BA,
∴若添加AD=BC,则可以判定△ADB≌△CBA(SAS),故选项A不符合题意;
若添加∠ABD=∠BAC,则可以判定△ADB≌△CBA(ASA),故选项B不符合题意;
若添加OA=OB,则∠DBA=∠CAB,故可以判定△ADB≌△CBA(ASA),故选项C不符合题意;
若添加AC=BD,则无法判断△ADB≌△CBA,故选项D符合题意;
故选:D.
12.【解答】解:在△ABC与△DEB中,
AC=BDAB=EDBC=BE,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即12∠AFB=∠ACB,
故选:D.
13.【解答】解:A、由AB∥CD,可得∠DCA=∠CAB,且∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项A不符合题意;
B、由AB=CD,且∠1=∠2,AC=AC,不能判定△ADC≌△CBA,故选项B符合题意;
C、由AD=BC,且∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项C不符合题意;
D,由∠B=∠D,且∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项D不符合题意;
故选:B.
14.【解答】解:∵BE=CF,
∴BE+CE=CF+CE,
∴BC=EF,
当AB∥DE时,∠B=∠DEF,依据SAS即可得到△ABC≌△DEF;
当∠A=∠D或BE=EC或AC∥DF时,不能使△ABC≌△DEF;
故选:B.
15.【解答】解:∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=45°,
∴∠ABD=∠DAB,
∴BD=AD,
∵∠CAD+∠AFE=90°,∠CAD+∠C=90°,∠AFE=∠BFD,
∴∠AFE=∠C,
∵∠AFE=∠BFD
∴∠C=∠BFD
在△BDF和△ADC中,
∠C=∠BFDAD=BD∠BDF=∠ADC,
∴△BDF≌△ADC(AAS),
∴DF=CD=4,
故选:B.
16.【解答】解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
AM=BK∠A=∠BAK=BN,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:D.
17.【解答】解:
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE,
∴当AB=DE时,可利用AAS判定△ABC≌△DEF,故A能判断,故A不符合题意;
当AC=DF时,可利用AAS判定△ABC≌△DEF,故B能判断,故B不符合题意;
当∠A=∠D时,两三角形没有对应边相等,故C不能判断,故C符合题意;
当BF=EC时,可得BC=EF,利用ASA可判定△ABC≌△DEF,故D能判断,故D不符合题意;
故选:C.
18.【解答】解:已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是AD=CF,可以得到AC=DF,根据SAS可以证明△ABC≌△DEF,故选项A不符合题意;
已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是∠BCA=∠EFD,根据AAS可以证明△ABC≌△DEF,故选项B不符合题意;
已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是∠B=∠E,根据ASA可以证明△ABC≌△DEF,故选项C不符合题意;
已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是BC=EF,根据SSA不可以证明△ABC≌△DEF,故选项D符合题意;
故选:D.
19.【解答】解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是四边形没有稳定性.
故选:D.
20.【解答】解:∵AB∥ED,AB=DE,
∴∠B=∠E,
∴当BF=EC时,
可得BC=EF,
可利用“SAS”判断△ABC≌△DEF.
故选:A.
21.【解答】解:
在△AOD和△BOC中
OA=OB∠AOD=∠BOCOD=OC
∴△AOD≌△BOC(SAS),
∴∠A=∠B,
∵OC=OD,OA=OB,
∴AC=BD,
在△ACE和△BDE中
∠A=∠B∠AEC=∠BEDAC=BD
∴△ACE≌△BDE(AAS),
∴AE=BE,
在△AOE和△BOE中
OA=OB∠A=∠BAE=BE
∴△AOE≌△BOE(SAS),
∴∠COE=∠DOE,
在△COE和△DOE中
OC=OD∠COE=∠DOEOE=OE
∴△COE≌△DOE(SAS),
故全等的三角形有4对,
故选:C.
22.【解答】解:A、添加BC=EC,∠B=∠E可用SAS判定两个三角形全等,故A选项正确;
B、添加BC=EC,AC=DC可用SSS判定两个三角形全等,故B选项正确;
C、添加∠B=∠E,∠A=∠D可用ASA判定两个三角形全等,故C选项正确;
D、添加BC=EC,∠A=∠D后是SSA,无法证明三角形全等,故D选项错误.
故选:D.
23.【解答】解:A、全等三角形是指形状相同、大小相等的两个三角形,故本选项错误;
B、全等三角形的面积相等,但是面积相等的两个三角形不一定全等,故本选项错误;
C、边长相等的两个等边三角形是全等三角形,故本选项错误;
D、全等三角形是指两个能完全重合的三角形,故本选项正确.
故选:D.
24.【解答】解:∵AD=BE,
∴AD+BD=BD+BE,即AB=DE,
∵BC=EF,
∴当添加∠ABC=∠E时,可根据“SAS”判断△ABC≌△DEF;
当添加AC=∠DF时,可根据“SSS”判断△ABC≌△DEF;
当添加∠C=∠F时,可根据“ASA”判断△ABC≌△DEF.
故选:C.
25.【解答】解:∵EF⊥AC,CF⊥AB,
∴∠A+∠ACD=90°,∠F+∠ECF=90°,
∴∠A=∠F,且CE=CB=3cm,∠ACB=∠FEC=90°,
∴△ACB≌△FEC(AAS)
∴AC=EF=7cm,
∴AE=4cm,
故选:B.
26.【解答】解:∵AE=DF,
∴AE+EF=DF+EF,
∴AF=DE,
∵AB∥CD,
∴∠A=∠D,
在△BAF和△CDE中,AB=DC∠A=∠DAF=DE,
∴△BAF≌△CDE(SAS),
在△BAE和△CDF中,AB=DC∠A=∠DAE=DF,
∴△BAE≌△CDF(SAS),
∴BE=CF,∠AEB=∠DFC,
∴∠BEF=∠CFE,
在△BEF和△CFE中,BE=CF∠BEF=∠CFEEF=FE,
∴△BEF≌△CFE(SAS),
即全等三角形有3对,
故选:C.
27.【解答】解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,∠BCA=∠DCA,BC=CD,AB=AD,
∴AC平分∠BAD,AC平分∠BCD,AC垂直平分BD,故A,B,C正确,
但AO不一定等于CO,故D错误,
故选:D.
28.【解答】解:∵AC⊥BC,ED⊥AB,
∴∠C=∠ADE=90°,
在△ACE和△ADE中,
∠C=∠ADE∠CAE=∠DAEAE=AE,
∴△ACE≌△ADE(AAS),
∴AD=AC=3cm,
∴BD=AB﹣AD=4cm,
故选:B.
29.【解答】解:A:两个面积相等的图形不一定是全等图形,故A错误;
B:长方形不一定是全等图形,故B错误;
C:两个全等图形形状一定相同,故C正确;
D:两个正方形不一定是全等图形,故D错误;
故选:C.
30.【解答】解:根据题意知,BC边为公共边.
A、由“SSS”可以判定△ABC≌△DCB,故本选项错误;
B、由“SAS”可以判定△ABC≌△DCB,故本选项错误;
C、由“SSA”不能判定△ABC≌△DCB,故本选项正确;
D、∠DBC=∠ACB,∠A=∠D,则由“AAS”可以判定△ABC≌△DCB,故本选项错误.
故选:C.
31.【解答】解:当△APC≌△BQP时,AP=BQ,即18﹣x=2x,
解得:x=6;
当△APC≌△BPQ时,AP=BP=12AB=9米,
此时所用时间为9秒,AC=BQ=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故选:B.
32.【解答】解:
∵△ABC和△DEF全等,AC=DF=b,DE=AB=a,
∴∠1=∠B,∠A=∠D=50°,∠F=∠C=72°,
∴∠1=180°﹣∠D﹣∠F=58°,
故选:B.
33.【解答】解:A、符合判定HL,故本选项正确,不符合题意;
B、全等三角形的判定必须有边的参与,故本选项错误,符合题意;
C、符合判定AAS,故本选项正确,不符合题意;
D、符合判定SAS,故本选项正确,不符合题意.
故选:B.
34.【解答】解:A、正确.
∵AD=AE
∴∠ADE=∠AED
∵BE=CD
∴△ABE≌△ACD(SAS)
B、正确.
∵△ABE≌△ACD
∴AB=AC,∠B=∠C
∵BD=CE
∴△ABD≌△ACE(SAS)
C、错误.
∵∠ADB=∠AEC=100°
∴∠ADE=∠AED=80°
∴∠DAE=20°
D、正确.
∵∠BAE=70°
∴∠BAD=50°
∵∠ADB=∠AEC=100°
∴∠B=∠C=30°
故选:C.
35.【解答】解:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
∠A=∠BAE=BE∠AEC=∠BED,
∴△AEC≌△BED(ASA).
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=38°,
∴∠C=∠EDC=71°,
∴∠BDE=∠C=71°.
故选:A.
36.【解答】解:∵△ABC≌△MNP,∠A=∠M,∠C=∠P,
∴∠B=∠N,BC=NP,
∵BC=2,
∴NP=2.
故选:A.
一.选择题(共36小题)
1.(2019秋?宿松县校级期末)在如图所示的6×6网格中,△ABC是格点三角形(即顶点恰好是网格线的交点),则与△ABC有一条公共边且全等(不含△ABC)的所有格点三角形的个数是( )
A.3个 B.4个 C.6个 D.7个
2.(2019秋?石台县期末)已知图中的两个三角形全等,则∠1等于( )
A.70° B.50° C.60° D.120°
3.(2019秋?蜀山区期末)如图,∠BDA=∠BDC,现添加以下哪个条件不能判定△ABD≌△CBD的是( )
A.∠A=∠C B.∠ABD=∠CBD C.AB=CB D.AD=CD
4.(2019秋?蜀山区期末)如图,D是AB延长线上一点,DF交AC于点E,AE=CE,FC∥AB,若AB=3,CF=5,则BD的长是( )
A.0.5 B.1 C.1.5 D.2
5.(2019秋?蜀山区期末)如图,△ABC≌△DEC,点E在边AB上,∠DEC=75°,则∠BCE的度数是( )
A.25° B.30° C.40° D.75°
6.(2019秋?肥东县期末)已知△ABC如图所示,另有△DEF,满足ED=AB,DF=AC,∠E=∠B.下列结论一定正确的是( )
A.BC=EF
B.∠C=∠F
C.△ABC中BC边上的高=△DEF中EF边上的高
D.△ABC中BC边上的中线=△DEF中EF边上的中线
7.(2019秋?肥东县期末)如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性这样做的道理是( )
A.两点之间的所有连线中线段最短
B.三角形具有稳定性
C.经过两点有一条直线,并且只有一条直线拉杆
D.在连接直线外一点与直线上各点的线段中,垂线段最短
8.(2019秋?谢家集区期末)如图,已知AB=DE,∠1=∠2.若要得到△ABC≌△DEF,则下列条件中不符合要求的是( )
A.∠A=∠D B.∠C=∠F C.AC=DF D.CE=FB
9.(2019秋?肥东县期末)如图,△ABC≌△DBE,点D在线段AC上,线段BC与DE交于点F下面各项中,不能推导出的结论是( )
A.∠EBF=∠ABD B.∠EBF=∠FDC C.∠ABD=∠FDC D.∠ABD=∠FBD
10.(2019秋?包河区期末)如图所示,在△ABC和△DEF中,AB=DE,∠A=∠D,若证△ABC≌△DEF还要从下列条件中补选一个,错误的选法是( )
A.∠ABC=∠DEF B.∠ACB=∠DFE C.AC=DF D.BC=EF
11.(2019秋?无为县期末)如图,AC与BD相交于点O,∠DAB=∠CBA,添加下列哪一个条件后,仍不能使△ADB≌△CBA的是( )
A.AD=BC B.∠ABD=∠BAC C.OA=OB D.AC=BD
12.(2019秋?瑶海区期末)如图,在△ABC和△DEB中,点C在BD边上,AC与BE交于F.若AB=DE,BC=BE,AC=BD,则∠ACB等于( )
A.∠D B.∠E C.2∠ABF D.12∠AFB
13.(2019秋?当涂县期末)如图,已知∠1=∠2,下列添加的条件不能使△ADC≌△CBA的是( )
A.AB∥DC B.AB=CD C.AD=BC D.∠B=∠D
14.(2019秋?义安区期末)如图,已知AB=DE,BE=CF,添加下列条件中哪一个能使△ABC≌△DEF( )
A.∠A=∠D B.AB∥DE C.BE=EC D.AC∥DF
15.(2019秋?田家庵区期末)如图,已知△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长度为( )
A.3 B.4 C.5 D.6
16.(2019秋?全椒县期末)如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
17.(2019秋?蚌埠期末)如图、点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AB=DE B.AC=DF C.∠A=∠D D.BF=EC
18.(2019秋?裕安区期末)如图,点A,D,C,F在一条直线上,AB=DE,∠A=∠EDF,下列条件不能判定△ABC≌△DEF的是( )
A.AD=CF B.∠BCA=∠F C.∠B=∠E D.BC=EF
19.(2019秋?裕安区期末)如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )
A.A,C两点之间 B.G,H两点之间
C.B,F两点之间 D.E,G两点之间
20.(2019秋?颍州区期末)如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
A.BF=EC B.AC=DF C.∠B=∠E D.BF=FC
21.(2019秋?太湖县期末)如图,已知OA=OB,OC=OD,AD和BC相交于点E,则图中共有全等三角形的对数( )
A.2对 B.3对 C.4对 D.5对
22.(2019秋?宣城期末)如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是( )
A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D D.BC=EC,∠A=∠D
23.(2019秋?长丰县期末)下列说法正确的是( )
A.全等三角形是指形状相同的两个三角形
B.全等三角形是指面积相等的两个三角形
C.两个等边三角形是全等三角形
D.全等三角形是指两个能完全重合的三角形
24.(2018秋?滁州期末)如图,在△ABC和△DEF中,BC=EF,点A,D,B,E在一条直线上,且AD=BE,添加下列条件不能判定△ABC≌△DEF的是( )
A.∠ABC=∠E B.AC=DF C.∠A=∠FDE D.∠C=∠F=90°
25.(2018秋?滁州期末)如图,在Rt△ABC中,∠ACB=90°,BC=3cm,CD⊥AB,在AC上取一点E,使CE=BC,过点E作EF⊥AC交CD的延长线于点F,若EF=7cm,则AE的长是( )
A.5cm B.4cm C.3cm D.2cm
26.(2018秋?长丰县期末)如图,点A,E,F,D在同一直线上,AB∥CD,AB=CD,AE=DF,则图中全等三角形共有( )
A.1对 B.2对 C.3对 D.4对
27.(2018秋?蜀山区期末)如图,△ABC≌△ADC,AC、BD相交于点O,下列结论不一定正确的是( )
A.AC平分∠BAD B.AC平分∠BCD C.AC平分BD D.BD平分AC
28.(2018秋?颍上县期末)如图,在△ABC中,AC⊥BC,AE为∠BAC的平分线,ED⊥AB于点D,AB=7cm,AC=3cm,则BD的长为( )
A.3cm B.4cm C.1cm D.2cm
29.(2018秋?无为县期末)下列说法正确的是( )
A.两个面积相等的图形一定是全等图形
B.两个长方形是全等图形
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
30.(2018秋?阜南县期末)如图,下列条件中,不能证明△ABC≌△DCB的条件是( )
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.AB=DC,∠DBC=∠ACB D.∠DBC=∠ACB,∠A=∠D
31.(2018秋?宣城期末)如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4 B.6 C.4或9 D.6或9
32.(2018秋?寿县期末)已知图中的两个三角形全等,则∠1等于( )
A.50° B.58° C.60° D.72°
33.(2018秋?太湖县期末)下列条件,不能判定两个直角三角形全等的是( )
A.斜边和一直角边对应相等
B.两个锐角对应相等
C.一锐角和斜边对应相等
D.两条直角边对应相等
34.(2017秋?濉溪县期末)如图,AD=AE,BE=CD,∠ADB=∠AEC=100°,∠BAE=70°,下列结论错误的是( )
A.△ABE≌△ACD B.△ABD≌△ACE C.∠DAE=40° D.∠C=30°
35.(2017秋?蜀山区期末)如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )
A.71° B.76° C.78° D.80°
36.(2017秋?望江县期末)若△ABC≌△MNP,∠A=∠M,∠C=∠P,AB=4cm,BC=2cm,则NP=( )
A.2cm B.3cm C.4cm D.6cm
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第14章《全等三角形》选择题精选
参考答案与试题解析
一.选择题(共36小题)
1.【解答】解:如图所示:一共有7个符合题意的点.
故选:D.
2.【解答】解:∵△ABC≌△DEF,
∴∠E=∠B=70°,
∴∠1=180°﹣50°﹣70°=60°,
故选:C.
3.【解答】解:∵∠BDA=∠BDC,BD=BD,
∴当添加∠A=∠C时,可根据“AAS”判断△ABD≌△CBD;
当添加∠ABD=∠CBD时,可根据“ASA”判断△ABD≌△CBD;
当添加AD=CD时,可根据“SAS”判断△ABD≌△CBD.
故选:C.
4.【解答】证明:∵FC∥AB
∴∠FCE=∠DAE,
在△CFE和△ADE中
∠FCE=∠DAECE=AE∠CEF=∠AED,
∴△CFE≌△ADE(ASA),
∴AD=CF=5,
∵AB=3,
∴BD=5﹣3=2,
故选:D.
5.【解答】解:∵△ABC≌△DEC,
∴∠B=∠DEC=75°,CE=CB,
∴∠CEB=∠B=75°,∠B=∠CEB,
∴∠BCE=180°﹣2×75°=30°,
故选:B.
6.【解答】解:如图,过点A作AH⊥BC于H,过点D作DG⊥EF于G,
∵AB=DE,∠B=∠E,∠AHB=∠DGE,
∴△ABH≌△DEG(AAS)
∴AH=DG,
∴△ABC中BC边上的高=△DEF中EF边上的高,
故选:C.
7.【解答】解:人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性这样做的道理是三角形具有稳定性,
故选:B.
8.【解答】解:A、添加∠A=∠D,根据ASA可以判定△ABC≌△DEF,故本选项不符合题意.
B、添加∠C=∠F,根据AAS可以判定△ABC≌△DEF,故本选项不符合题意.
C、添加AC=DF,根据SSA不可以判定△ABC≌△DEF,故本选项符合题意.
D、添加CE=FB可以得到BC=EF,根据SAS可以判定△ABC≌△DEF,故本选项不符合题意.
故选:C.
9.【解答】解:∵△ABC≌△DBE,
∴∠EBD=∠CBA,∠A=∠BDE,
∴∠EBF=∠ABD,故A不合题意;
∵AB=BD,
∴∠A=∠BDF=∠BDE,
∴∠A+∠ADB=∠ADB+∠BDE,
∴∠EBF=∠FDC=∠EBF,故B,C不合题意;
无法得出∠ABD=∠FBD,故此选项符合题意.
故选:D.
10.【解答】解:∵AB=DE,∠A=∠D,∠ABC=∠DEF,
∴△ABC≌△DEF(ASA),
故A选项不符合题意;
∵AB=DE,∠A=∠D,∠ACB=∠DFE,
∴△ABC≌△DEF(AAS),
故B选项不符合题意;
∵AB=DE,∠A=∠D,AC=DF,
∴△ABC≌△DEF(SAS),
故C选项不符合题意;
∵AB=DE,∠A=∠D,BC=EF,
无法证明△ABC与△DEF全等,
故D选项符合题意;
故选:D.
11.【解答】解:∵∠DAB=∠CBA,AB=BA,
∴若添加AD=BC,则可以判定△ADB≌△CBA(SAS),故选项A不符合题意;
若添加∠ABD=∠BAC,则可以判定△ADB≌△CBA(ASA),故选项B不符合题意;
若添加OA=OB,则∠DBA=∠CAB,故可以判定△ADB≌△CBA(ASA),故选项C不符合题意;
若添加AC=BD,则无法判断△ADB≌△CBA,故选项D符合题意;
故选:D.
12.【解答】解:在△ABC与△DEB中,
AC=BDAB=EDBC=BE,
∴△ABC≌△DEB(SSS),
∴∠ACB=∠EBD.
∵∠AFB是△BFC的外角,
∴∠AFB=∠ACB+∠EBD,
∴∠AFB=2∠ACB,即12∠AFB=∠ACB,
故选:D.
13.【解答】解:A、由AB∥CD,可得∠DCA=∠CAB,且∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项A不符合题意;
B、由AB=CD,且∠1=∠2,AC=AC,不能判定△ADC≌△CBA,故选项B符合题意;
C、由AD=BC,且∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项C不符合题意;
D,由∠B=∠D,且∠1=∠2,AC=AC,能判定△ADC≌△CBA,故选项D不符合题意;
故选:B.
14.【解答】解:∵BE=CF,
∴BE+CE=CF+CE,
∴BC=EF,
当AB∥DE时,∠B=∠DEF,依据SAS即可得到△ABC≌△DEF;
当∠A=∠D或BE=EC或AC∥DF时,不能使△ABC≌△DEF;
故选:B.
15.【解答】解:∵AD⊥BC,
∴∠ADB=90°,
∵∠ABC=45°,
∴∠ABD=∠DAB,
∴BD=AD,
∵∠CAD+∠AFE=90°,∠CAD+∠C=90°,∠AFE=∠BFD,
∴∠AFE=∠C,
∵∠AFE=∠BFD
∴∠C=∠BFD
在△BDF和△ADC中,
∠C=∠BFDAD=BD∠BDF=∠ADC,
∴△BDF≌△ADC(AAS),
∴DF=CD=4,
故选:B.
16.【解答】解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
AM=BK∠A=∠BAK=BN,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:D.
17.【解答】解:
∵AB∥ED,AC∥FD,
∴∠B=∠E,∠ACB=∠DFE,
∴当AB=DE时,可利用AAS判定△ABC≌△DEF,故A能判断,故A不符合题意;
当AC=DF时,可利用AAS判定△ABC≌△DEF,故B能判断,故B不符合题意;
当∠A=∠D时,两三角形没有对应边相等,故C不能判断,故C符合题意;
当BF=EC时,可得BC=EF,利用ASA可判定△ABC≌△DEF,故D能判断,故D不符合题意;
故选:C.
18.【解答】解:已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是AD=CF,可以得到AC=DF,根据SAS可以证明△ABC≌△DEF,故选项A不符合题意;
已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是∠BCA=∠EFD,根据AAS可以证明△ABC≌△DEF,故选项B不符合题意;
已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是∠B=∠E,根据ASA可以证明△ABC≌△DEF,故选项C不符合题意;
已知点A、D、C、F在同一直线上,AB=DE,∠A=∠EDF,添加的一个条件是BC=EF,根据SSA不可以证明△ABC≌△DEF,故选项D符合题意;
故选:D.
19.【解答】解:工人师傅做了一个长方形窗框ABCD,工人师傅为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在E、G两点之间(没有构成三角形),这种做法根据的是四边形没有稳定性.
故选:D.
20.【解答】解:∵AB∥ED,AB=DE,
∴∠B=∠E,
∴当BF=EC时,
可得BC=EF,
可利用“SAS”判断△ABC≌△DEF.
故选:A.
21.【解答】解:
在△AOD和△BOC中
OA=OB∠AOD=∠BOCOD=OC
∴△AOD≌△BOC(SAS),
∴∠A=∠B,
∵OC=OD,OA=OB,
∴AC=BD,
在△ACE和△BDE中
∠A=∠B∠AEC=∠BEDAC=BD
∴△ACE≌△BDE(AAS),
∴AE=BE,
在△AOE和△BOE中
OA=OB∠A=∠BAE=BE
∴△AOE≌△BOE(SAS),
∴∠COE=∠DOE,
在△COE和△DOE中
OC=OD∠COE=∠DOEOE=OE
∴△COE≌△DOE(SAS),
故全等的三角形有4对,
故选:C.
22.【解答】解:A、添加BC=EC,∠B=∠E可用SAS判定两个三角形全等,故A选项正确;
B、添加BC=EC,AC=DC可用SSS判定两个三角形全等,故B选项正确;
C、添加∠B=∠E,∠A=∠D可用ASA判定两个三角形全等,故C选项正确;
D、添加BC=EC,∠A=∠D后是SSA,无法证明三角形全等,故D选项错误.
故选:D.
23.【解答】解:A、全等三角形是指形状相同、大小相等的两个三角形,故本选项错误;
B、全等三角形的面积相等,但是面积相等的两个三角形不一定全等,故本选项错误;
C、边长相等的两个等边三角形是全等三角形,故本选项错误;
D、全等三角形是指两个能完全重合的三角形,故本选项正确.
故选:D.
24.【解答】解:∵AD=BE,
∴AD+BD=BD+BE,即AB=DE,
∵BC=EF,
∴当添加∠ABC=∠E时,可根据“SAS”判断△ABC≌△DEF;
当添加AC=∠DF时,可根据“SSS”判断△ABC≌△DEF;
当添加∠C=∠F时,可根据“ASA”判断△ABC≌△DEF.
故选:C.
25.【解答】解:∵EF⊥AC,CF⊥AB,
∴∠A+∠ACD=90°,∠F+∠ECF=90°,
∴∠A=∠F,且CE=CB=3cm,∠ACB=∠FEC=90°,
∴△ACB≌△FEC(AAS)
∴AC=EF=7cm,
∴AE=4cm,
故选:B.
26.【解答】解:∵AE=DF,
∴AE+EF=DF+EF,
∴AF=DE,
∵AB∥CD,
∴∠A=∠D,
在△BAF和△CDE中,AB=DC∠A=∠DAF=DE,
∴△BAF≌△CDE(SAS),
在△BAE和△CDF中,AB=DC∠A=∠DAE=DF,
∴△BAE≌△CDF(SAS),
∴BE=CF,∠AEB=∠DFC,
∴∠BEF=∠CFE,
在△BEF和△CFE中,BE=CF∠BEF=∠CFEEF=FE,
∴△BEF≌△CFE(SAS),
即全等三角形有3对,
故选:C.
27.【解答】解:∵△ABC≌△ADC,
∴∠BAC=∠DAC,∠BCA=∠DCA,BC=CD,AB=AD,
∴AC平分∠BAD,AC平分∠BCD,AC垂直平分BD,故A,B,C正确,
但AO不一定等于CO,故D错误,
故选:D.
28.【解答】解:∵AC⊥BC,ED⊥AB,
∴∠C=∠ADE=90°,
在△ACE和△ADE中,
∠C=∠ADE∠CAE=∠DAEAE=AE,
∴△ACE≌△ADE(AAS),
∴AD=AC=3cm,
∴BD=AB﹣AD=4cm,
故选:B.
29.【解答】解:A:两个面积相等的图形不一定是全等图形,故A错误;
B:长方形不一定是全等图形,故B错误;
C:两个全等图形形状一定相同,故C正确;
D:两个正方形不一定是全等图形,故D错误;
故选:C.
30.【解答】解:根据题意知,BC边为公共边.
A、由“SSS”可以判定△ABC≌△DCB,故本选项错误;
B、由“SAS”可以判定△ABC≌△DCB,故本选项错误;
C、由“SSA”不能判定△ABC≌△DCB,故本选项正确;
D、∠DBC=∠ACB,∠A=∠D,则由“AAS”可以判定△ABC≌△DCB,故本选项错误.
故选:C.
31.【解答】解:当△APC≌△BQP时,AP=BQ,即18﹣x=2x,
解得:x=6;
当△APC≌△BPQ时,AP=BP=12AB=9米,
此时所用时间为9秒,AC=BQ=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故选:B.
32.【解答】解:
∵△ABC和△DEF全等,AC=DF=b,DE=AB=a,
∴∠1=∠B,∠A=∠D=50°,∠F=∠C=72°,
∴∠1=180°﹣∠D﹣∠F=58°,
故选:B.
33.【解答】解:A、符合判定HL,故本选项正确,不符合题意;
B、全等三角形的判定必须有边的参与,故本选项错误,符合题意;
C、符合判定AAS,故本选项正确,不符合题意;
D、符合判定SAS,故本选项正确,不符合题意.
故选:B.
34.【解答】解:A、正确.
∵AD=AE
∴∠ADE=∠AED
∵BE=CD
∴△ABE≌△ACD(SAS)
B、正确.
∵△ABE≌△ACD
∴AB=AC,∠B=∠C
∵BD=CE
∴△ABD≌△ACE(SAS)
C、错误.
∵∠ADB=∠AEC=100°
∴∠ADE=∠AED=80°
∴∠DAE=20°
D、正确.
∵∠BAE=70°
∴∠BAD=50°
∵∠ADB=∠AEC=100°
∴∠B=∠C=30°
故选:C.
35.【解答】解:∵AE和BD相交于点O,
∴∠AOD=∠BOE.
在△AOD和△BOE中,
∠A=∠B,∴∠BEO=∠2.
又∵∠1=∠2,
∴∠1=∠BEO,
∴∠AEC=∠BED.
在△AEC和△BED中,
∠A=∠BAE=BE∠AEC=∠BED,
∴△AEC≌△BED(ASA).
∴EC=ED,∠C=∠BDE.
在△EDC中,
∵EC=ED,∠1=38°,
∴∠C=∠EDC=71°,
∴∠BDE=∠C=71°.
故选:A.
36.【解答】解:∵△ABC≌△MNP,∠A=∠M,∠C=∠P,
∴∠B=∠N,BC=NP,
∵BC=2,
∴NP=2.
故选:A.
