2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章轴对称图形与等腰三角形选择题精选(Word版含答案)
文档属性
| 名称 | 2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章轴对称图形与等腰三角形选择题精选(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 168.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 18:48:04 | ||
图片预览

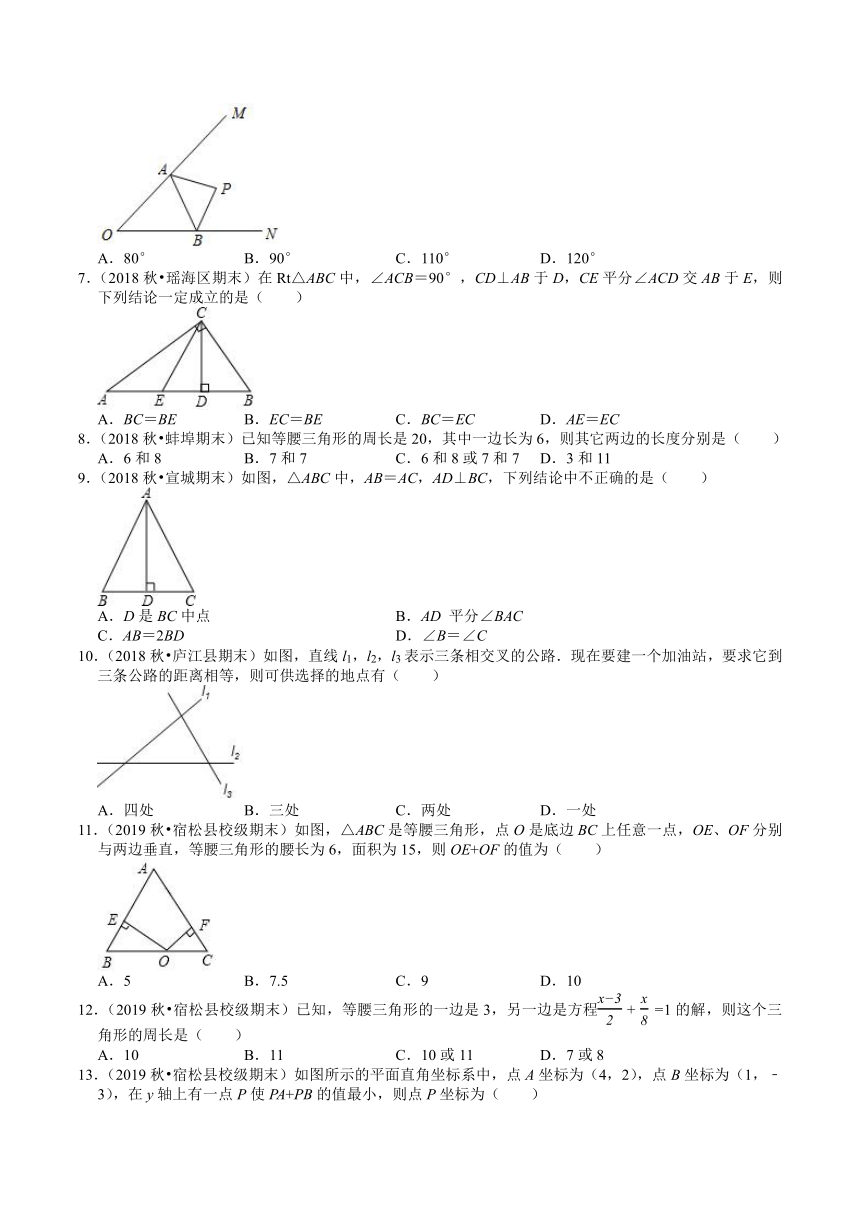



文档简介
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章《轴对称图形与等腰三角形》选择题精选
一.选择题(共35小题)
1.(2019秋?蜀山区期末)在△ABC中,与∠A相邻的外角是130°,要使△ABC为等腰三角形,则∠B的度数是( )
A.50° B.65°
C.50°或65° D.50°或65°或80°
2.(2019秋?义安区期末)如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=a,则∠A2020B2020O=( )
A.a22020 B.a22019 C.4040a D.4038a
3.(2019秋?芜湖期末)如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
4.(2018秋?义安区期末)如图,△ABC中,AB=AC=8cm,AB的垂直平分线MN交AC于D,△DBC的周长是14cm,则BC的长是( )
A.4 cm B.6 cm C.8 cm D.10 cm
5.(2018秋?宣城期末)如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,则∠CDE的度数为( )
A.15° B.20° C.25° D.30°
6.(2018秋?怀宁县期末)如图,∠MON=45°,P为∠MON内一点,A为OM上一点,B为ON上一点,当△PAB的周长取最小值时,∠APB的度数为( )
A.80° B.90° C.110° D.120°
7.(2018秋?瑶海区期末)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=BE B.EC=BE C.BC=EC D.AE=EC
8.(2018秋?蚌埠期末)已知等腰三角形的周长是20,其中一边长为6,则其它两边的长度分别是( )
A.6和8 B.7和7 C.6和8或7和7 D.3和11
9.(2018秋?宣城期末)如图,△ABC中,AB=AC,AD⊥BC,下列结论中不正确的是( )
A.D是BC中点 B.AD 平分∠BAC
C.AB=2BD D.∠B=∠C
10.(2018秋?庐江县期末)如图,直线l1,l2,l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( )
A.四处 B.三处 C.两处 D.一处
11.(2019秋?宿松县校级期末)如图,△ABC是等腰三角形,点O是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形的腰长为6,面积为15,则OE+OF的值为( )
A.5 B.7.5 C.9 D.10
12.(2019秋?宿松县校级期末)已知,等腰三角形的一边是3,另一边是方程x-32+x8=1的解,则这个三角形的周长是( )
A.10 B.11 C.10或11 D.7或8
13.(2019秋?宿松县校级期末)如图所示的平面直角坐标系中,点A坐标为(4,2),点B坐标为(1,﹣3),在y轴上有一点P使PA+PB的值最小,则点P坐标为( )
A.(2,0) B.(﹣2,0) C.(0,2) D.(0,﹣2)
14.(2020春?当涂县期末)已知a,b,c是△ABC的三边长,且满足a-6+|b﹣8|+(c﹣10)2=0,则△ABC是( )
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.以c为底边的等腰三角形
15.(2020春?蜀山区期末)已知,在△ABC中,∠A:∠B:∠C=1:2:3,BC=a,AC=b,AB=c,则下列结论错误的是( )
A.c=3b B.c=2a C.b2=3a2 D.a2+b2=c2
16.(2020春?瑶海区期末)如图,在四边形ABCD中,AB=BC=CD,∠ABC=160°,∠BCD=80°,△PDC为等边三角形,则∠ADC的度数为( )
A.70° B.75° C.80° D.85°
17.(2019秋?石台县期末)如图,△ABC的面积为12,AB=AC,BC=4,AC的垂直平分线EF分别交AB,AC边于点E,F,若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为( )
A.6 B.8 C.10 D.12
18.(2019秋?当涂县期末)已知等腰三角形的周长是22,其中一边长为8,则其它两边的长度分别是( )
A.3和11 B.7和7
C.6和8或7和7 D.3和11或7和7
19.(2019秋?宣城期末)已知等腰三角形的周长为16,其中一边长为3,则该等腰三角形的腰长为( )
A.3 B.10 C.6.5 D.3或6.5
20.(2019秋?谢家集区期末)等腰三角形的周长为14cm,其中一边长为4cm,则该等腰三角形的腰长为( )
A.4cm B.5cm C.4cm或5cm D.4cm或6cm
21.(2019秋?濉溪县期末)如图,已知等边△ABC的周长是12,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,则PD+PE+PF的值是( )
A.12 B.8 C.4 D.3
22.(2019秋?无为县期末)长方形按如图所示折叠,点D折叠到点D′的位置,已知∠D′FC=60°,则∠EFD等于( )
A.30° B.45° C.50° D.60°
23.(2019秋?潜山市期末)一个等腰三角形的周长为8,且三条边长均为整数,则腰长为( )
A.5 B.4 C.3 D.2
24.(2019秋?瑶海区期末)如图,在△ABC中,点D、E在BC边上,点F在AC边上,将△ABD沿着AD翻折,使点B和点E重合,将△CEF沿着EF翻折,点C恰与点A重合.结论:①∠BAC=90°,②DE=EF,③∠B=2∠C,④AB=EC,正确的有( )
A.①②③④ B.③④ C.①②④ D.①②③
25.(2019秋?瑶海区期末)下列图形是轴对称图形的是( )
A. B. C. D.
26.(2019秋?瑶海区期末)如图所示的钢架中,∠A=18°,P1A=P1P2,焊上等长的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架.∠P5P4B的度数是( )
A.80° B.85° C.90° D.100°
27.(2019秋?瑶海区期末)如图,△ABC中,DE垂直平分AC,交AC于E,交BC于D,连接AD,AE=4cm,则△ABC的周长与△ABD的周长差为( )
A.2cm B.4cm C.6cm D.8cm
28.(2019秋?无为县期末)在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.
A.5 B.6 C.7 D.8
29.(2019秋?义安区期末)若等腰三角形的两边长分别是3和10,则它的周长是( )
A.16 B.23 C.16或23 D.13
30.(2019秋?芜湖期末)如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A.2 B.2.5 C.3 D.4
31.(2019秋?蚌埠期末)如图,AD是等边△ABC的中线,AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
32.(2019秋?全椒县期末)如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1 cm B.2 cm C.3 cm D.4cm
33.(2019秋?蜀山区期末)等腰三角形的两边长分别为3cm和7cm,则周长为( )
A.13cm B.17cm C.13cm或17cm D.11cm或17cm
34.(2019秋?长丰县期末)如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边垂直平分线的交点处
35.(2018秋?濉溪县期末)如图,在等边三角形ABC中,∠DFE=120°,那么AD与CE的大小关系是( )
A.AD>CE B.AD<CE C.AD=CE D.不能确定
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章《轴对称图形与等腰三角形》选择题精选
参考答案与试题解析
一.选择题(共35小题)
1.【解答】解:∠A=180°﹣130°=50°.
当AB=AC时,∠B=∠C=12(180°﹣50°)=65°;
当BC=BA时,∠A=∠C=50°,则∠B=180°﹣50°﹣50°=80°;
当CA=CB时,∠A=∠B=50°.
∠B的度数为50°或65°或80°,
故选:D.
2.【解答】解:∵B1A2=B1B2,∠A1B1O=α,
∴∠A2B2O=12α,
同理∠A3B3O=12∠A2B2O=122α,
∠A4B4O=123α,
∴∠AnBnO=12n-1α,
∴∠A2020B2020O=α22019,
故选:B.
3.【解答】解:过点C作CE⊥AB于点E,交BD于点M′,过点M作MN′⊥BC于N′,
∵BD平分∠ABC,M′E⊥AB于点E,M′N′⊥BC于N
∴M′N′=M′E,
∴CE=CM′+M′E
∴当点M与M′重合,点N与N′重合时,CM+MN的最小值.
∵三角形ABC的面积为8,AB=4,
∴12×4?CE=8,
∴CE=4.
即CM+MN的最小值为4.
故选:B.
4.【解答】解:∵AB的垂直平分线MN交AC于D,
∴AD=BD,
∵AB=AC=8cm,△DBC的周长是14cm,
∴BC+CD+BD=BC+CD+AD=BC+AC=14cm,
∴BC=6cm.
故选:B.
5.【解答】解:∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD=40°,∠ADC=90°,
又∵AD=AE,
∴∠ADE=12(180°﹣∠CAD)=70°,
∴∠CDE=90°﹣70°=20°,
故选:B.
6.【解答】解:如图,作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°﹣∠MON=180°﹣45°=135°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°﹣∠P1PP2=45°,
∴∠APB=135°﹣45°=90°.
故选:B.
7.【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE.
故选:A.
8.【解答】解:当腰为6时,另一腰也为6,则底为20﹣2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20﹣6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
9.【解答】解:∵AB=AC,AD⊥BC,
∴∠B=∠C,∠BAD=∠CAD,BD=DC.
∴AD平分∠BAC,
无法确定AB=2BD.
故A、B、D正确,C错误.
故选:C.
10.【解答】解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三角形外角平分线的交点,共三处.
故选:A.
11.【解答】解:连接AO,如图,
∵AB=AC=6,
∴S△ABC=S△ABO+S△AOC=12AB?OE+12AC?OF=15,
∵AB=AC,
∴12AB(OE+OF)=15,
∴OE+OF=5.
故选:A.
12.【解答】解:x-32+x8=1,
4(x﹣3)+x=8,
4x﹣12+x=8,
4x+x=8+12,
5x=20,
x=4,
当等腰三角形的腰为4,底边为3时,这个三角形的周长=4+4+3=11,
当等腰三角形的腰为3,底边为4时,这个三角形的周长=4+3+3=10.
所以这个三角形的周长是10或11.
故选:C.
13.【解答】解:如图所示:作B点关于y轴对称点B′点,连接AB′,交y轴于点P,则此时AP+PB=AP+PB′=AB′的值最小,
∵点B坐标为(1,﹣3),
∴B′(﹣1,﹣3),
∴B′C=AC=5,
∴∠AB′C=45°,
∴PD=B′D=1,
∵OD=|﹣3|=3,
∴OP=2,
∴P(0,﹣2),
故选:D.
14.【解答】解:由题意得,a﹣6=0,b﹣8=0,c﹣10=0,
解得a=6,b=8,c=10,
∵62+82=100=102,
∴a2+b2=c2,
∴∠ACB=90°,
故选:C.
15.【解答】解:∵在△ABC中,∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∵BC=a,AC=b,AB=c,
∴a2+b2=c2,c=2a,ba=tan60°=3,bc=sin60°=32,
∴b=3a,c=233b
∴b2=3a2,
故B、C、D均正确,A错误.
故选:A.
16.【解答】解:∵△PDC为等边三角形;
∴∠PCD=∠DPC=∠CDP=60°,且PC=CD=PD,
∵AB=BC=CD,
∴AB=CP,
∵∠BCD=80°,
∴∠BCP=∠BCD﹣∠DCP=80°﹣60°=20°,
∵∠ABC=160°,
∴∠ABC+∠BCP=180°,
∴PC∥AB,
∵AB=CP,
∴四边形ABCP为平行四边形,
∴∠APC=∠ABC=160°,AP=BC,
∴AP=DP,∠APD=360°﹣∠CPD﹣∠APC=140°,
∴∠PDA=∠PAD=180°-∠APD2=20°,
∴∠ADC=∠CDP+∠ADP=60°+20°=80°,
故选:C.
17.【解答】解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×4×AD=12,
解得AD=6,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CP+PD的最小值,
∴△CDP的周长最短=(CP+PD)+CD=AD+12BC=6+12×4=6+2=8.
故选:B.
18.【解答】解:当腰为8时,另一腰也为8,则底为22﹣2×8=6,
∵6+8=14>8,
∴三边能构成三角形.
当底为8时,腰为(22﹣8)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
19.【解答】解:(1)当3是腰长时,底边为16﹣3×2=10,
此时3+3=6<10,不能组成三角形;
(2)当3是底边时,腰长为12×(16﹣3)=6.5,
此时3,6.5,6.5三边能够组成三角形.
所以腰长为6.5.
故选:C.
20.【解答】解:∵当腰是4cm时,则另两边是4cm,6cm;
当底边是4cm时,另两边长是5cm,5cm.
∴该等腰三角形的腰长为4cm或5cm.
故选:C.
21.【解答】解:延长EP、FP分别交AB、BC于G、H,
则由PD∥AB,PE∥BC,PF∥AC,可得,
四边形PGBD,EPHC是平行四边形,
∴PG=BD,PE=HC,
又△ABC是等边三角形,
又有PF∥AC,PD∥AB可得△PFG,△PDH是等边三角形,
∴PF=PG=BD,PD=DH,
又△ABC的周长为12,
∴PD+PE+PF=DH+HC+BD=BC=13×12=4,
故选:C.
22.【解答】解:根据翻折不变性得∠EFD=∠EFD′,
∵∠D′FC=60°,∠DFE+∠EFD′+∠D′FC=180°,
∴2∠EFD=180°﹣60°=120°,
∴∠EFD=60°.
故选:D.
23.【解答】解:设腰长为x,则底边为8﹣2x.
∵8﹣2x﹣x<x<8﹣2x+x,
∴2<x<4,
∵三边长均为整数,
∴x可取的值为:3.
故选:C.
24.【解答】解:∵将△ABD沿着AD翻折,使点B和点E重合,
∴AB=AE,∠B=∠AEB,
∵将△CEF沿着EF翻折,点C恰与点A重合,
∴AE=CE,∠C=∠CAE,
∴AB=EC,∴④正确;
∵∠AEB=∠C+∠CAE=2∠C,
∴∠B=2∠C,故③正确;
故选:B.
25.【解答】解:A、不是轴对称图形,本选项不符合题意;
B、是轴对称图形,本选项符合题意;
C、不是轴对称图形,本选项不符合题意;
D、不是轴对称图形,本选项不符合题意.
故选:B.
26.【解答】解:∵AP1=P1P2,P1P2=P2P3,P3P4=P2P3,P3P4=P4P5,
∴∠A=∠P1P2A,∠P2P1P3=∠P2P3P1,∠P3P2P4=∠P3P4P2,∠P4P3P5=∠P4P5P3,
∴∠P3P5P4=4∠A,
∵∠A=18°,
∴∠P3P5P4=72°,
∴∠P5P4B=90°.
故选:C.
27.【解答】解:∵DE垂直平分边AC,AE=4cm,
∴AD=CD,AC=2AE=8cm,
∵△ABC的周长=AB+AC+BC,
∵△ABD的周长=AB+AD+BD=AB+BC,
∴△ABC的周长与△ABD的周长差AC=8cm.
故选:D.
28.【解答】解:如图,最多能画出7个格点三角形与△ABC成轴对称.
故选:C.
29.【解答】解:∵等腰三角形的两边分别是3和10,
∴应分为两种情况:①3为底,10为腰,则3+10+10=23;
②10为底,3腰,而3+3<10,应舍去,
∴三角形的周长是23.
故选:B.
30.【解答】解:过P点作PF⊥OD,
∵∠AOB=150°,OC平分∠AOB,
∴∠DOP=∠POE=75°,
∵DP∥OA,
∴∠DPO=∠POE=75°,
∴∠DOP=∠DPO﹣75°,
∴DP=OD=4,
∴∠PDO=180°﹣75°﹣75°=30°,
∵PF⊥OD,
∴∠PFD=90°,
∴PF=12DP=2,
∵PE⊥OA,OC平分∠AOB,
∴PE=PF=2,
故选:A.
31.【解答】解:∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=12∠BAC=12×60°=30°,
∴∠ADC=90°,
∵AD=AE,
∴∠ADE=∠AED=180°-∠CAD2=75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
故选:D.
32.【解答】解:∵MN是线段AB的垂直平分线,
∴AN=BN,
∵△BCN的周长是7cm,
∴BN+NC+BC=7(cm),
∴AN+NC+BC=7(cm),
∵AN+NC=AC,
∴AC+BC=7(cm),
又∵AC=4cm,
∴BC=7﹣4=3(cm).
故选:C.
33.【解答】解:当7为腰时,周长=7+7+3=17cm;
当3为腰时,因为3+3<7,所以不能构成三角形;
故三角形的周长是17cm.
故选:B.
34.【解答】解:根据角平分线的性质,集贸市场应建在∠A、∠B两内角平分线的交点处.
故选:A.
35.【解答】解:AD=CE,
理由:∵△ABC是等边三角形,
∴∠A=∠ACB=60°,
∵∠DFE=120°,
∴∠EFC=60°,
∴∠BDC=60°+∠ACD,∠AEF=40°+∠ACE,
∴∠BDC=∠AEB,
∴∠ADE=∠BEC,
∵AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE.
故选:C.
一.选择题(共35小题)
1.(2019秋?蜀山区期末)在△ABC中,与∠A相邻的外角是130°,要使△ABC为等腰三角形,则∠B的度数是( )
A.50° B.65°
C.50°或65° D.50°或65°或80°
2.(2019秋?义安区期末)如图,在射线OA,OB上分别截取OA1=OB1,连接A1B1,在B1A1,B1B上分别截取B1A2=B1B2,连接A2B2,…按此规律作下去,若∠A1B1O=a,则∠A2020B2020O=( )
A.a22020 B.a22019 C.4040a D.4038a
3.(2019秋?芜湖期末)如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是( )
A.2 B.4 C.6 D.8
4.(2018秋?义安区期末)如图,△ABC中,AB=AC=8cm,AB的垂直平分线MN交AC于D,△DBC的周长是14cm,则BC的长是( )
A.4 cm B.6 cm C.8 cm D.10 cm
5.(2018秋?宣城期末)如图,在△ABC中,AB=AC,AD⊥BC,∠BAD=40°,AD=AE,则∠CDE的度数为( )
A.15° B.20° C.25° D.30°
6.(2018秋?怀宁县期末)如图,∠MON=45°,P为∠MON内一点,A为OM上一点,B为ON上一点,当△PAB的周长取最小值时,∠APB的度数为( )
A.80° B.90° C.110° D.120°
7.(2018秋?瑶海区期末)在Rt△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACD交AB于E,则下列结论一定成立的是( )
A.BC=BE B.EC=BE C.BC=EC D.AE=EC
8.(2018秋?蚌埠期末)已知等腰三角形的周长是20,其中一边长为6,则其它两边的长度分别是( )
A.6和8 B.7和7 C.6和8或7和7 D.3和11
9.(2018秋?宣城期末)如图,△ABC中,AB=AC,AD⊥BC,下列结论中不正确的是( )
A.D是BC中点 B.AD 平分∠BAC
C.AB=2BD D.∠B=∠C
10.(2018秋?庐江县期末)如图,直线l1,l2,l3表示三条相交叉的公路.现在要建一个加油站,要求它到三条公路的距离相等,则可供选择的地点有( )
A.四处 B.三处 C.两处 D.一处
11.(2019秋?宿松县校级期末)如图,△ABC是等腰三角形,点O是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形的腰长为6,面积为15,则OE+OF的值为( )
A.5 B.7.5 C.9 D.10
12.(2019秋?宿松县校级期末)已知,等腰三角形的一边是3,另一边是方程x-32+x8=1的解,则这个三角形的周长是( )
A.10 B.11 C.10或11 D.7或8
13.(2019秋?宿松县校级期末)如图所示的平面直角坐标系中,点A坐标为(4,2),点B坐标为(1,﹣3),在y轴上有一点P使PA+PB的值最小,则点P坐标为( )
A.(2,0) B.(﹣2,0) C.(0,2) D.(0,﹣2)
14.(2020春?当涂县期末)已知a,b,c是△ABC的三边长,且满足a-6+|b﹣8|+(c﹣10)2=0,则△ABC是( )
A.以a为斜边的直角三角形
B.以b为斜边的直角三角形
C.以c为斜边的直角三角形
D.以c为底边的等腰三角形
15.(2020春?蜀山区期末)已知,在△ABC中,∠A:∠B:∠C=1:2:3,BC=a,AC=b,AB=c,则下列结论错误的是( )
A.c=3b B.c=2a C.b2=3a2 D.a2+b2=c2
16.(2020春?瑶海区期末)如图,在四边形ABCD中,AB=BC=CD,∠ABC=160°,∠BCD=80°,△PDC为等边三角形,则∠ADC的度数为( )
A.70° B.75° C.80° D.85°
17.(2019秋?石台县期末)如图,△ABC的面积为12,AB=AC,BC=4,AC的垂直平分线EF分别交AB,AC边于点E,F,若点D为BC边的中点,点P为线段EF上一动点,则△PCD周长的最小值为( )
A.6 B.8 C.10 D.12
18.(2019秋?当涂县期末)已知等腰三角形的周长是22,其中一边长为8,则其它两边的长度分别是( )
A.3和11 B.7和7
C.6和8或7和7 D.3和11或7和7
19.(2019秋?宣城期末)已知等腰三角形的周长为16,其中一边长为3,则该等腰三角形的腰长为( )
A.3 B.10 C.6.5 D.3或6.5
20.(2019秋?谢家集区期末)等腰三角形的周长为14cm,其中一边长为4cm,则该等腰三角形的腰长为( )
A.4cm B.5cm C.4cm或5cm D.4cm或6cm
21.(2019秋?濉溪县期末)如图,已知等边△ABC的周长是12,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,则PD+PE+PF的值是( )
A.12 B.8 C.4 D.3
22.(2019秋?无为县期末)长方形按如图所示折叠,点D折叠到点D′的位置,已知∠D′FC=60°,则∠EFD等于( )
A.30° B.45° C.50° D.60°
23.(2019秋?潜山市期末)一个等腰三角形的周长为8,且三条边长均为整数,则腰长为( )
A.5 B.4 C.3 D.2
24.(2019秋?瑶海区期末)如图,在△ABC中,点D、E在BC边上,点F在AC边上,将△ABD沿着AD翻折,使点B和点E重合,将△CEF沿着EF翻折,点C恰与点A重合.结论:①∠BAC=90°,②DE=EF,③∠B=2∠C,④AB=EC,正确的有( )
A.①②③④ B.③④ C.①②④ D.①②③
25.(2019秋?瑶海区期末)下列图形是轴对称图形的是( )
A. B. C. D.
26.(2019秋?瑶海区期末)如图所示的钢架中,∠A=18°,P1A=P1P2,焊上等长的钢条P1P2,P2P3,P3P4,P4P5…来加固钢架.∠P5P4B的度数是( )
A.80° B.85° C.90° D.100°
27.(2019秋?瑶海区期末)如图,△ABC中,DE垂直平分AC,交AC于E,交BC于D,连接AD,AE=4cm,则△ABC的周长与△ABD的周长差为( )
A.2cm B.4cm C.6cm D.8cm
28.(2019秋?无为县期末)在4×4的正方形网格中,以格点为顶点的三角形称为格点三角形,在图中画出与△ABC关于某条直线对称的格点三角形,最多能画( )个.
A.5 B.6 C.7 D.8
29.(2019秋?义安区期末)若等腰三角形的两边长分别是3和10,则它的周长是( )
A.16 B.23 C.16或23 D.13
30.(2019秋?芜湖期末)如图,∠AOB=150°,OC平分∠AOB,P为OC上一点,PD∥OA交OB于点D,PE⊥OA于点E.若OD=4,则PE的长为( )
A.2 B.2.5 C.3 D.4
31.(2019秋?蚌埠期末)如图,AD是等边△ABC的中线,AE=AD,则∠EDC的度数为( )
A.30° B.20° C.25° D.15°
32.(2019秋?全椒县期末)如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
A.1 cm B.2 cm C.3 cm D.4cm
33.(2019秋?蜀山区期末)等腰三角形的两边长分别为3cm和7cm,则周长为( )
A.13cm B.17cm C.13cm或17cm D.11cm或17cm
34.(2019秋?长丰县期末)如图,三条公路把A、B、C三个村庄连成一个三角形区域,某地区决定在这个三角形区域内修建一个集贸市场,要使集贸市场到三个条公路的距离相等,则这个集贸市场应建在( )
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边中线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边垂直平分线的交点处
35.(2018秋?濉溪县期末)如图,在等边三角形ABC中,∠DFE=120°,那么AD与CE的大小关系是( )
A.AD>CE B.AD<CE C.AD=CE D.不能确定
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章《轴对称图形与等腰三角形》选择题精选
参考答案与试题解析
一.选择题(共35小题)
1.【解答】解:∠A=180°﹣130°=50°.
当AB=AC时,∠B=∠C=12(180°﹣50°)=65°;
当BC=BA时,∠A=∠C=50°,则∠B=180°﹣50°﹣50°=80°;
当CA=CB时,∠A=∠B=50°.
∠B的度数为50°或65°或80°,
故选:D.
2.【解答】解:∵B1A2=B1B2,∠A1B1O=α,
∴∠A2B2O=12α,
同理∠A3B3O=12∠A2B2O=122α,
∠A4B4O=123α,
∴∠AnBnO=12n-1α,
∴∠A2020B2020O=α22019,
故选:B.
3.【解答】解:过点C作CE⊥AB于点E,交BD于点M′,过点M作MN′⊥BC于N′,
∵BD平分∠ABC,M′E⊥AB于点E,M′N′⊥BC于N
∴M′N′=M′E,
∴CE=CM′+M′E
∴当点M与M′重合,点N与N′重合时,CM+MN的最小值.
∵三角形ABC的面积为8,AB=4,
∴12×4?CE=8,
∴CE=4.
即CM+MN的最小值为4.
故选:B.
4.【解答】解:∵AB的垂直平分线MN交AC于D,
∴AD=BD,
∵AB=AC=8cm,△DBC的周长是14cm,
∴BC+CD+BD=BC+CD+AD=BC+AC=14cm,
∴BC=6cm.
故选:B.
5.【解答】解:∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD=40°,∠ADC=90°,
又∵AD=AE,
∴∠ADE=12(180°﹣∠CAD)=70°,
∴∠CDE=90°﹣70°=20°,
故选:B.
6.【解答】解:如图,作出P点关于OM、ON的对称点P1,P2连接P1,P2交OM,ON于A、B两点,此时△PAB的周长最小,由题意可知∠P1PP2=180°﹣∠MON=180°﹣45°=135°,
∴∠P1PA+∠P2PB=∠P1+∠P2=180°﹣∠P1PP2=45°,
∴∠APB=135°﹣45°=90°.
故选:B.
7.【解答】解:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠A=90°,
∴∠BCD=∠A.
∵CE平分∠ACD,
∴∠ACE=∠DCE.
又∵∠BEC=∠A+∠ACE,∠BCE=∠BCD+∠DCE,
∴∠BEC=∠BCE,
∴BC=BE.
故选:A.
8.【解答】解:当腰为6时,另一腰也为6,则底为20﹣2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20﹣6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
9.【解答】解:∵AB=AC,AD⊥BC,
∴∠B=∠C,∠BAD=∠CAD,BD=DC.
∴AD平分∠BAC,
无法确定AB=2BD.
故A、B、D正确,C错误.
故选:C.
10.【解答】解:满足条件的有:
(1)三角形两个内角平分线的交点,共一处;
(2)三角形外角平分线的交点,共三处.
故选:A.
11.【解答】解:连接AO,如图,
∵AB=AC=6,
∴S△ABC=S△ABO+S△AOC=12AB?OE+12AC?OF=15,
∵AB=AC,
∴12AB(OE+OF)=15,
∴OE+OF=5.
故选:A.
12.【解答】解:x-32+x8=1,
4(x﹣3)+x=8,
4x﹣12+x=8,
4x+x=8+12,
5x=20,
x=4,
当等腰三角形的腰为4,底边为3时,这个三角形的周长=4+4+3=11,
当等腰三角形的腰为3,底边为4时,这个三角形的周长=4+3+3=10.
所以这个三角形的周长是10或11.
故选:C.
13.【解答】解:如图所示:作B点关于y轴对称点B′点,连接AB′,交y轴于点P,则此时AP+PB=AP+PB′=AB′的值最小,
∵点B坐标为(1,﹣3),
∴B′(﹣1,﹣3),
∴B′C=AC=5,
∴∠AB′C=45°,
∴PD=B′D=1,
∵OD=|﹣3|=3,
∴OP=2,
∴P(0,﹣2),
故选:D.
14.【解答】解:由题意得,a﹣6=0,b﹣8=0,c﹣10=0,
解得a=6,b=8,c=10,
∵62+82=100=102,
∴a2+b2=c2,
∴∠ACB=90°,
故选:C.
15.【解答】解:∵在△ABC中,∠A:∠B:∠C=1:2:3,
∴∠A=30°,∠B=60°,∠C=90°,
∵BC=a,AC=b,AB=c,
∴a2+b2=c2,c=2a,ba=tan60°=3,bc=sin60°=32,
∴b=3a,c=233b
∴b2=3a2,
故B、C、D均正确,A错误.
故选:A.
16.【解答】解:∵△PDC为等边三角形;
∴∠PCD=∠DPC=∠CDP=60°,且PC=CD=PD,
∵AB=BC=CD,
∴AB=CP,
∵∠BCD=80°,
∴∠BCP=∠BCD﹣∠DCP=80°﹣60°=20°,
∵∠ABC=160°,
∴∠ABC+∠BCP=180°,
∴PC∥AB,
∵AB=CP,
∴四边形ABCP为平行四边形,
∴∠APC=∠ABC=160°,AP=BC,
∴AP=DP,∠APD=360°﹣∠CPD﹣∠APC=140°,
∴∠PDA=∠PAD=180°-∠APD2=20°,
∴∠ADC=∠CDP+∠ADP=60°+20°=80°,
故选:C.
17.【解答】解:连接AD,
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×4×AD=12,
解得AD=6,
∵EF是线段AC的垂直平分线,
∴点C关于直线EF的对称点为点A,
∴AD的长为CP+PD的最小值,
∴△CDP的周长最短=(CP+PD)+CD=AD+12BC=6+12×4=6+2=8.
故选:B.
18.【解答】解:当腰为8时,另一腰也为8,则底为22﹣2×8=6,
∵6+8=14>8,
∴三边能构成三角形.
当底为8时,腰为(22﹣8)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
19.【解答】解:(1)当3是腰长时,底边为16﹣3×2=10,
此时3+3=6<10,不能组成三角形;
(2)当3是底边时,腰长为12×(16﹣3)=6.5,
此时3,6.5,6.5三边能够组成三角形.
所以腰长为6.5.
故选:C.
20.【解答】解:∵当腰是4cm时,则另两边是4cm,6cm;
当底边是4cm时,另两边长是5cm,5cm.
∴该等腰三角形的腰长为4cm或5cm.
故选:C.
21.【解答】解:延长EP、FP分别交AB、BC于G、H,
则由PD∥AB,PE∥BC,PF∥AC,可得,
四边形PGBD,EPHC是平行四边形,
∴PG=BD,PE=HC,
又△ABC是等边三角形,
又有PF∥AC,PD∥AB可得△PFG,△PDH是等边三角形,
∴PF=PG=BD,PD=DH,
又△ABC的周长为12,
∴PD+PE+PF=DH+HC+BD=BC=13×12=4,
故选:C.
22.【解答】解:根据翻折不变性得∠EFD=∠EFD′,
∵∠D′FC=60°,∠DFE+∠EFD′+∠D′FC=180°,
∴2∠EFD=180°﹣60°=120°,
∴∠EFD=60°.
故选:D.
23.【解答】解:设腰长为x,则底边为8﹣2x.
∵8﹣2x﹣x<x<8﹣2x+x,
∴2<x<4,
∵三边长均为整数,
∴x可取的值为:3.
故选:C.
24.【解答】解:∵将△ABD沿着AD翻折,使点B和点E重合,
∴AB=AE,∠B=∠AEB,
∵将△CEF沿着EF翻折,点C恰与点A重合,
∴AE=CE,∠C=∠CAE,
∴AB=EC,∴④正确;
∵∠AEB=∠C+∠CAE=2∠C,
∴∠B=2∠C,故③正确;
故选:B.
25.【解答】解:A、不是轴对称图形,本选项不符合题意;
B、是轴对称图形,本选项符合题意;
C、不是轴对称图形,本选项不符合题意;
D、不是轴对称图形,本选项不符合题意.
故选:B.
26.【解答】解:∵AP1=P1P2,P1P2=P2P3,P3P4=P2P3,P3P4=P4P5,
∴∠A=∠P1P2A,∠P2P1P3=∠P2P3P1,∠P3P2P4=∠P3P4P2,∠P4P3P5=∠P4P5P3,
∴∠P3P5P4=4∠A,
∵∠A=18°,
∴∠P3P5P4=72°,
∴∠P5P4B=90°.
故选:C.
27.【解答】解:∵DE垂直平分边AC,AE=4cm,
∴AD=CD,AC=2AE=8cm,
∵△ABC的周长=AB+AC+BC,
∵△ABD的周长=AB+AD+BD=AB+BC,
∴△ABC的周长与△ABD的周长差AC=8cm.
故选:D.
28.【解答】解:如图,最多能画出7个格点三角形与△ABC成轴对称.
故选:C.
29.【解答】解:∵等腰三角形的两边分别是3和10,
∴应分为两种情况:①3为底,10为腰,则3+10+10=23;
②10为底,3腰,而3+3<10,应舍去,
∴三角形的周长是23.
故选:B.
30.【解答】解:过P点作PF⊥OD,
∵∠AOB=150°,OC平分∠AOB,
∴∠DOP=∠POE=75°,
∵DP∥OA,
∴∠DPO=∠POE=75°,
∴∠DOP=∠DPO﹣75°,
∴DP=OD=4,
∴∠PDO=180°﹣75°﹣75°=30°,
∵PF⊥OD,
∴∠PFD=90°,
∴PF=12DP=2,
∵PE⊥OA,OC平分∠AOB,
∴PE=PF=2,
故选:A.
31.【解答】解:∵AD是等边△ABC的中线,
∴AD⊥BC,∠BAD=∠CAD=12∠BAC=12×60°=30°,
∴∠ADC=90°,
∵AD=AE,
∴∠ADE=∠AED=180°-∠CAD2=75°,
∴∠EDC=∠ADC﹣∠ADE=90°﹣75°=15°.
故选:D.
32.【解答】解:∵MN是线段AB的垂直平分线,
∴AN=BN,
∵△BCN的周长是7cm,
∴BN+NC+BC=7(cm),
∴AN+NC+BC=7(cm),
∵AN+NC=AC,
∴AC+BC=7(cm),
又∵AC=4cm,
∴BC=7﹣4=3(cm).
故选:C.
33.【解答】解:当7为腰时,周长=7+7+3=17cm;
当3为腰时,因为3+3<7,所以不能构成三角形;
故三角形的周长是17cm.
故选:B.
34.【解答】解:根据角平分线的性质,集贸市场应建在∠A、∠B两内角平分线的交点处.
故选:A.
35.【解答】解:AD=CE,
理由:∵△ABC是等边三角形,
∴∠A=∠ACB=60°,
∵∠DFE=120°,
∴∠EFC=60°,
∴∠BDC=60°+∠ACD,∠AEF=40°+∠ACE,
∴∠BDC=∠AEB,
∴∠ADE=∠BEC,
∵AC=BC,
∴△ACD≌△CBE(AAS),
∴AD=CE.
故选:C.
