2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章轴对称图形与等腰三角形填空题精选(Word版含答案)
文档属性
| 名称 | 2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章轴对称图形与等腰三角形填空题精选(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 179.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 18:49:50 | ||
图片预览


文档简介
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章《轴对称图形与等腰三角形》填空题精选
一.填空题(共25小题)
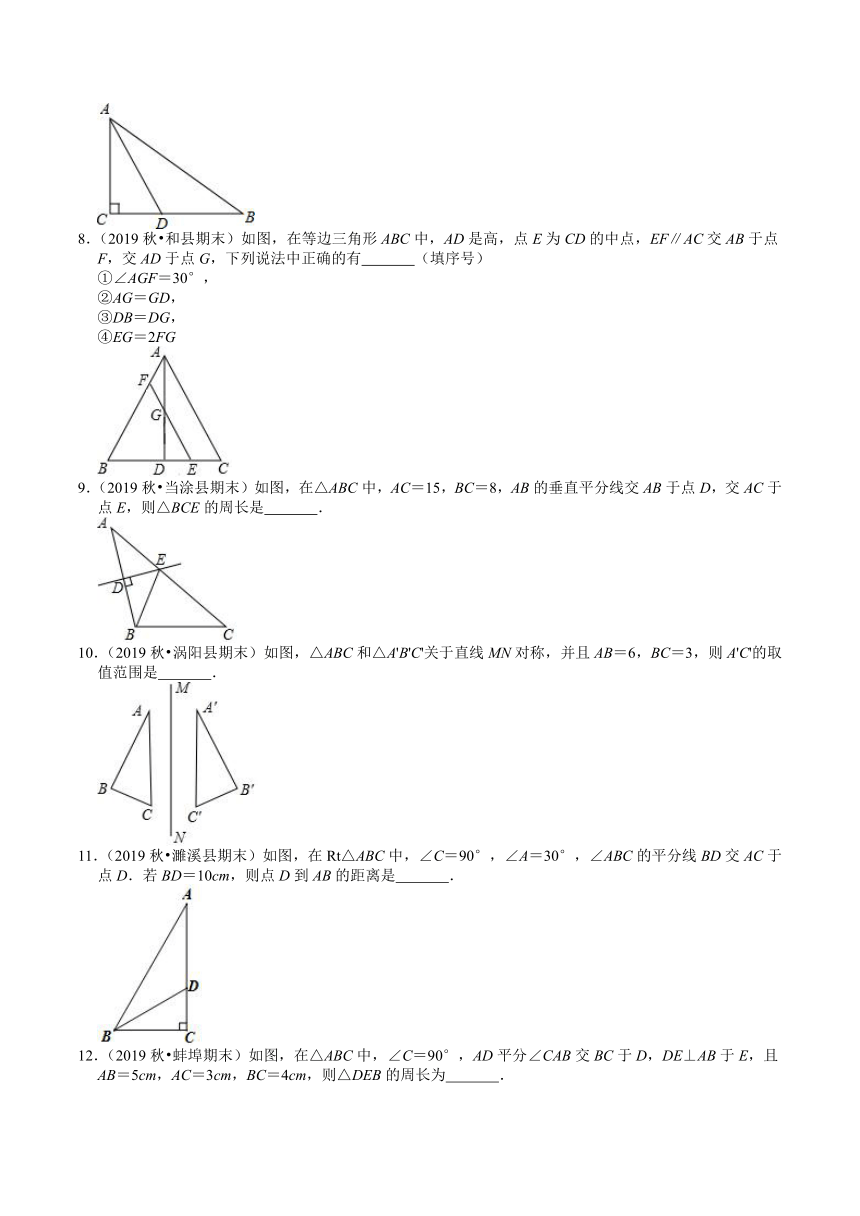
1.(2019秋?宿松县校级期末)已知:如图,△ABC中,BO平分∠ABC,CO平分∠ACB交BO于点O,过点O作DE∥BC交AB于点D,交AC于点E,则△ADE的周长可用△ABC的边表示为 .
2.(2020春?砀山县期末)如图,在△ABC中,AC=5cm,线段AB的垂直平分线交AC于点N,△BCN的周长是8cm,则BC= .
3.(2020春?砀山县期末)如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=5,BC=7,S△ABC=12,则DE的长为 .
4.(2019秋?宿松县期末)已知等腰三角形的周长是14,设其腰长是x,底边长是y,则y与x的函数关系式为y= ,自变量x的取值范围是 .
5.(2019秋?肥西县期末)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PD=2,则PC的长为 .
6.(2019秋?涡阳县期末)如图,在△ABC中,D是AB的中点,且CD⊥AB,∠A=45°,则∠B= .
7.(2019秋?和县期末)如图,在△ABC中,∠C=90°,∠A的平分线交BC于D,AC=4cm,DC=3cm,则点D到斜边AB的距离为 cm.
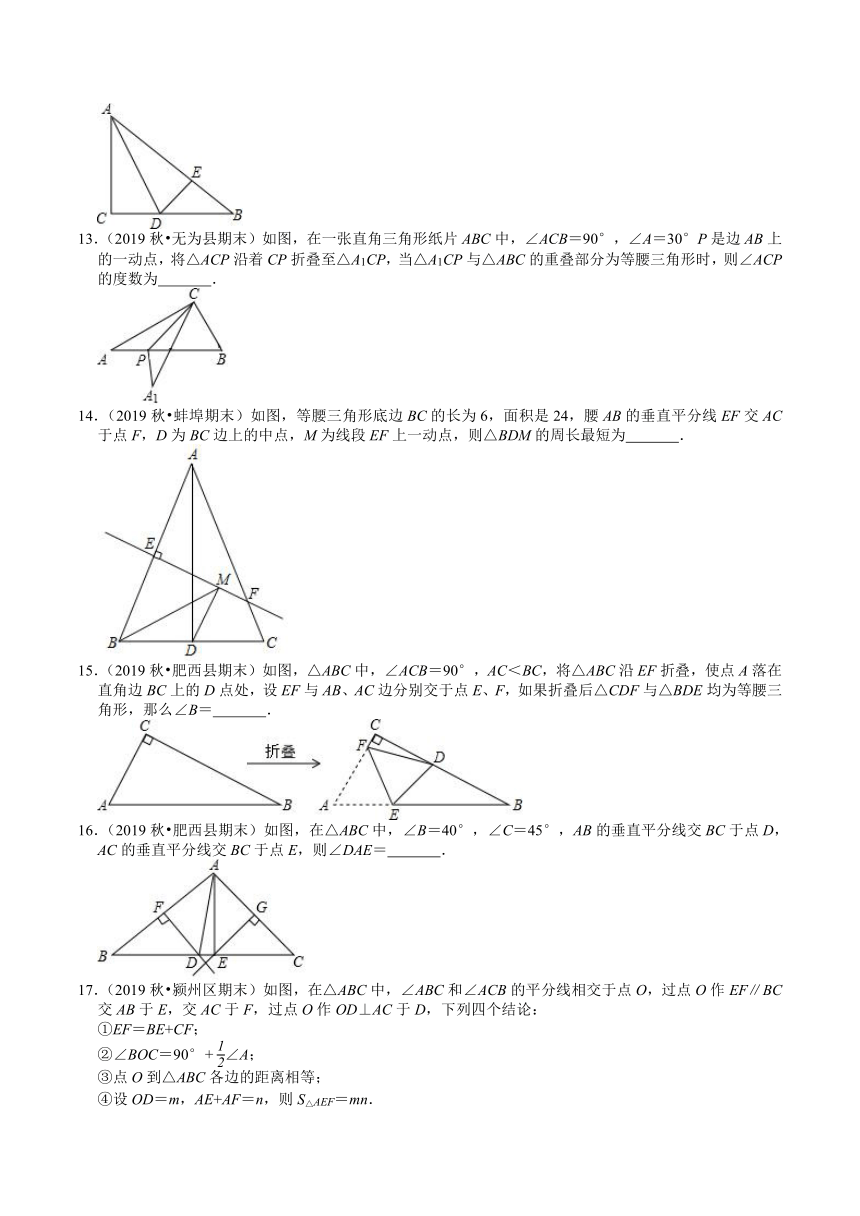
8.(2019秋?和县期末)如图,在等边三角形ABC中,AD是高,点E为CD的中点,EF∥AC交AB于点F,交AD于点G,下列说法中正确的有 (填序号)
①∠AGF=30°,
②AG=GD,
③DB=DG,
④EG=2FG
9.(2019秋?当涂县期末)如图,在△ABC中,AC=15,BC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是 .
10.(2019秋?涡阳县期末)如图,△ABC和△A'B'C'关于直线MN对称,并且AB=6,BC=3,则A'C'的取值范围是 .
11.(2019秋?濉溪县期末)如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于点D.若BD=10cm,则点D到AB的距离是 .
12.(2019秋?蚌埠期末)如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=5cm,AC=3cm,BC=4cm,则△DEB的周长为 .
13.(2019秋?无为县期末)如图,在一张直角三角形纸片ABC中,∠ACB=90°,∠A=30°P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP,当△A1CP与△ABC的重叠部分为等腰三角形时,则∠ACP的度数为 .
14.(2019秋?蚌埠期末)如图,等腰三角形底边BC的长为6,面积是24,腰AB的垂直平分线EF交AC于点F,D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为 .
15.(2019秋?肥西县期末)如图,△ABC中,∠ACB=90°,AC<BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B= .
16.(2019秋?肥西县期末)如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE= .
17.(2019秋?颍州区期末)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+12∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是 .(填序号)
18.(2019秋?蜀山区期末)如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若BD=6,则CD= .
19.(2019秋?宣城期末)如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,则MN的长为 cm.
20.(2019秋?濉溪县期末)如图,在△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,则DE等于 .
21.(2019秋?芜湖期末)如图,在△ABC中,∠ACB=90°,AB的垂直平分线DE交AB于E,交AC于D,∠DBC=30°,BD=4.6,则D到AB的距离为 .
22.(2019秋?芜湖期末)如图所示,△BDC′是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对.
23.(2018秋?庐江县期末)如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=12EC中,正确的是 .
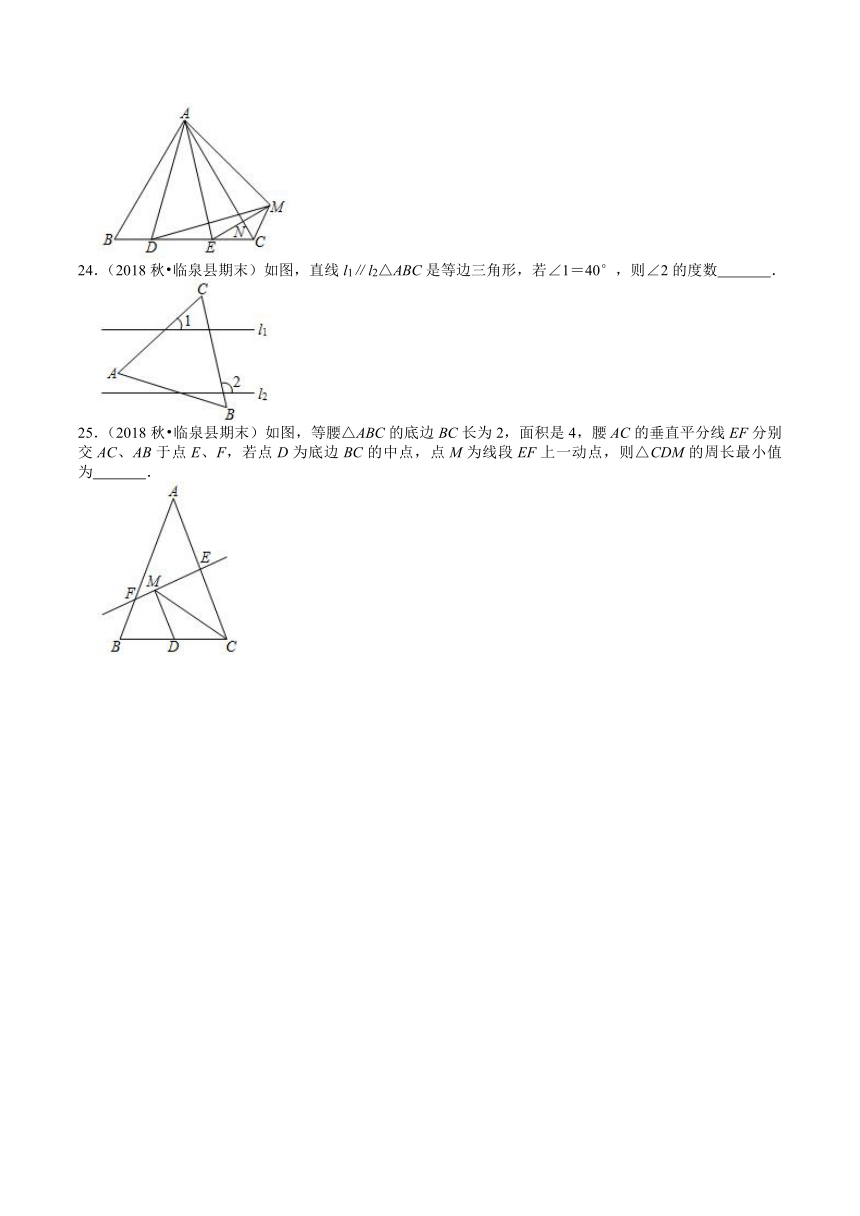
24.(2018秋?临泉县期末)如图,直线l1∥l2△ABC是等边三角形,若∠1=40°,则∠2的度数 .
25.(2018秋?临泉县期末)如图,等腰△ABC的底边BC长为2,面积是4,腰AC的垂直平分线EF分别交AC、AB于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△CDM的周长最小值为 .
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章《轴对称图形与等腰三角形》填空题精选
参考答案与试题解析
一.填空题(共25小题)
1.【解答】解:∵BO平分∠ABC,CO平分∠ACB,
∴∠DBO=∠OBC,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠OBC,∠COE=∠OCB,
∴∠DOB=∠DBO,∠EOC=∠OCE,
∴BD=DO,OE=CE,
∴△ADE的周长=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC
故答案为:AB+AC.
2.【解答】解:∵MN是线段AB的垂直平分线,
∴NA=NB,
∴AC=NA+NC=NB+NC=5,
∵△BCN的周长是8,
∴NB+NC+BC=8,
∴BC=8﹣5=3(cm),
故答案为:3cm.
3.【解答】解:作DF⊥AB于F,
∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DE=DF,
∴12×AB×DF+12×BC×DE=S△ABC,即12×5×DE+12×7×DE=12,
解得,DE=2,
故答案为:2.
4.【解答】解:∵2x+y=14,
∴y=14﹣2x,即x<7,
∵两边之和大于第三边
∴x>72,
综上可得72<x<7
故答案为:y=﹣2x+14,72<x<7.
5.【解答】解:作PE⊥OB于E,如图,
∵OP平分∠AOB,PD⊥OA,PE⊥OB,
∴PE=PD=2,
∵OP平分∠AOB,
∴∠AOB=2∠AOP=2×15°=30°,
∵PC∥OA,
∴∠ECP=∠AOB=30°,
∴PC=2PE=4.
故答案为4.
6.【解答】解:∵D是AB的中点,CD⊥AB,
∴CD是线段AB 的垂直平分线,
∴CA=CB,
∴∠B=∠A=45°,
故答案为:45°.
7.【解答】解:设D到AB的距离为h,
∵∠C=90°,
∴DC⊥AC,
∵AD平分∠CAB,DC=3cm,
∴h=DC=3cm,
故答案为:3.
8.【解答】解:∵△ABC是等边三角形,AD⊥BC,
∴∠DAC=30°.
∵EF∥AC,
∴∠AGF=∠DAC=30°,故①正确,
∵EG∥AC,DE=EC,
∴AG=DG,故②正确,
∵AD=3BD,
∴BD≠DG,故③错误,
设AC=a,
∵∠DAC=30°,
∴AD=AC?cos30°=32a;
∵点G为AD的中点,
∴GE是△ADC的中位线,
∴点E时CD的中点,
∴EF=34AC=34a,
∵EF=34AC=34a,GE=12AC=12a,
∴EG=2FG,故④正确.
故答案为①②④.
9.【解答】解:∵AB的垂直平分线交AB于点D,
∴EA=EB,
∴△BCE的周长=EB+EC+BC=EA+EC+BC=AC+BC=15+8=23.
故答案为23.
10.【解答】解:∵△ABC和△A′B′C′关于MN对称,
∴得出△ABC≌△A′B′C′,
∴AC=A′C′,
∵AB﹣BC<AC<AB+BC,
∴6﹣3<AC<6+3
∴A′C′的取值范围是:3<A′C′<9.
故答案为:3<A′C′<9.
11.【解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠CBD=12∠ABC=30°,
在Rt△BCD中,CD=12BD=12×10cm=5cm,
∵∠ABC的平分线BD交AC于点D,
∴点D到AB的距离为5cm.
故答案为5cm.
12.【解答】解:∵AD平分∠CAB交BC于D,DE⊥AB,DC⊥AC,
∴DC=DE,
在Rt△ADC和△ADE中
AD=ADDC=DE,
∴Rt△ADC≌△ADE(HL),
∴AE=AC=3,
∴BE=AB=5﹣3=2,
∴△DEB的周长=BE+BD+DE=BE+BD+CD=BE+BC=2+4=6(cm).
故答案为6cm.
13.【解答】解:当PC=CE时,如图1所示:
设∠ACP=x,则∠A1CP=x,
∵CP=CE,
∴∠CPE=∠CEP,
∵∠CPE=∠ACP+∠A=x+30°,
∴x+x+30°+x+30°=180°,
∴x=40°;
当CP=CE时,如图2所示:
设∠ACP=x.
则∠CPE=∠CEP=2x﹣90°+30°=2x﹣60°,
在△CPE中,90°﹣x+2(2x﹣60°)=180°,
解得:x=70°,
PE=PC不成立(因为∠CPE=x+30°>x,此时求得x=50°,点E应该在AB延长线上),
综上所述,∠ACP的度数为40°或70°,
故答案为:40°或70°.
14.【解答】解:∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×6×AD=24,解得AD=8,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+12BC=8+12×6=8+3=11.
故答案为11.
15.【解答】解:∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=12∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,如图1所示:
∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.
此时∠B=2x=45°,
∵AC<BC,
∴∠B=45°不成立;
②当BD=BE时,如图2所示:
则∠B=(180°﹣4x)°,∠CAB=60°,∠CAD=22.5°.
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,
此时∠B=(180﹣4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则∠B=12(180﹣2x)°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+12(180﹣2x)°,
此方程无解.
∴DE=BE不成立.
综上所述,∠B=30°.
故答案为:30°.
16.【解答】解:∵点D、E分别是AB、AC边的垂直平分线与BC的交点,
∴AD=BD,AE=CE,
∴∠B=∠BAD,∠C=∠CAE,
∵∠B=40°,∠C=45°,
∴∠B+∠C=85°,∠BAC=95°,
∴∠BAD+∠CAE=85°,
∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=95°﹣85°=10°,
故答案为:10°
17.【解答】解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=12∠ABC,∠OCB=12∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-12∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+12∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=12AE?OM+12AF?OD=12OD?(AE+AF)=12mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故答案是:①②③
18.【解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=180°﹣30°﹣90°=60°,
∵BD是∠ABC的平分线,
∴∠DBC=12∠ABC=30°,
∵∠C=90°,
∴CD=12BD=12×6=3,
故答案为:3.
19.【解答】解:连接AN、AM,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵EM是AB的垂直平分线,
∴MB=MA,
∴∠MAB=∠B=30°,
∴∠NMA=60°,
同理NA=NC,∠MNA=60°,
∴△MAN是等边三角形,
∴BM=MN=NC=13BC=2cm,
故答案为:2.
20.【解答】解:∵BI、CI分别平分∠ABC、∠ACF,
∴∠ABI=∠CBI,∠ECI=∠ICF,
∵DE∥BC,
∴∠DIB=∠CBI,∠EIC=∠ICF,
∴∠ABI=∠DIB,∠ECI=∠EIC,
∴DI=BD=8cm,EI=CE=5cm,
∴DE=DI﹣EI=3(cm).
故答案为:3cm.
21.【解答】解:∵DE垂直平分AB,
∴DB=DA,
∴∠A=∠ABD,
∵∠C=90°,∠DBC=30°,
∴∠A+∠ABD=90°﹣30°=60°,
∴∠ABD=30°,
在Rt△BED中,∠EBD=30°,BD=4.6,
∴DE=12BD=2.3,
即D到AB的距离为2.3.
故答案为2.3.
22.【解答】∵四边形ABCD是长方形,
∴∠A=∠C=90°,AB=CD,AD=BC,
∴△ABD≌△CDB.(HL)
∵△BDC是将长方形纸牌ABCD沿着BD折叠得到的,
∴BC′=AD,BD=BD,∠C′=∠A.
∴△ABD≌△C′DB.(HL)
同理△DCB≌△C′DB.
∵∠A=∠C′,∠AOB=∠C′OD,AB=C′D,
∴△AOB≌△C′OD.(AAS)
所以共有四对全等三角形.
23.【解答】解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=∠ACE=60°,
在△ABD和△ACE中,AB=AC∠B=∠ACEBD=CE,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE,AD=AE,故①正确;
由折叠的性质得:CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,
∴∠DAM=∠BAC=60°,
∴△ADM是等边三角形,
∴DM=AD,
∵AB>AD,
∴AB>DM,
∵∠ACD>∠DAC,
∴AD>DC,
∴△ABD与△DCM不全等,故③正确、②错误;
由折叠的性质得:AE=AM,CE=CM,
∴AC垂直平分EM,
∴∠ENC=90°,
∵∠ACE=60°,
∴∠CEN=30°,
∴CN=12EC,故④正确,
故答案为:①③④.
24.【解答】解:如图,
∵△ABC是等边三角形,
∴∠C=60°,
∵∠1=40°,
∴∠3=40°+60°=100°,
∵直线l1∥l2,
∴∠2=∠3=100°,
故答案为:100°.
25.【解答】解:连接AM、连接AD交EF与点M′.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×2×AD=4,解得AD=4,
∵EF是线段AB的垂直平分线,
∴AM=CM.
∴CM+MD=AM+MD.
∴当点M位于点M′处时,AM+MD有最小值,最小值即为AD=4.
∴△CDM的周长的最小值为CM+MD+CD=AD+CD=4+1=5.
故答案为5.
一.填空题(共25小题)
1.(2019秋?宿松县校级期末)已知:如图,△ABC中,BO平分∠ABC,CO平分∠ACB交BO于点O,过点O作DE∥BC交AB于点D,交AC于点E,则△ADE的周长可用△ABC的边表示为 .
2.(2020春?砀山县期末)如图,在△ABC中,AC=5cm,线段AB的垂直平分线交AC于点N,△BCN的周长是8cm,则BC= .
3.(2020春?砀山县期末)如图,BD平分∠ABC交AC于点D,DE⊥BC于点E,若AB=5,BC=7,S△ABC=12,则DE的长为 .
4.(2019秋?宿松县期末)已知等腰三角形的周长是14,设其腰长是x,底边长是y,则y与x的函数关系式为y= ,自变量x的取值范围是 .
5.(2019秋?肥西县期末)如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PD=2,则PC的长为 .
6.(2019秋?涡阳县期末)如图,在△ABC中,D是AB的中点,且CD⊥AB,∠A=45°,则∠B= .
7.(2019秋?和县期末)如图,在△ABC中,∠C=90°,∠A的平分线交BC于D,AC=4cm,DC=3cm,则点D到斜边AB的距离为 cm.
8.(2019秋?和县期末)如图,在等边三角形ABC中,AD是高,点E为CD的中点,EF∥AC交AB于点F,交AD于点G,下列说法中正确的有 (填序号)
①∠AGF=30°,
②AG=GD,
③DB=DG,
④EG=2FG
9.(2019秋?当涂县期末)如图,在△ABC中,AC=15,BC=8,AB的垂直平分线交AB于点D,交AC于点E,则△BCE的周长是 .
10.(2019秋?涡阳县期末)如图,△ABC和△A'B'C'关于直线MN对称,并且AB=6,BC=3,则A'C'的取值范围是 .
11.(2019秋?濉溪县期末)如图,在Rt△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于点D.若BD=10cm,则点D到AB的距离是 .
12.(2019秋?蚌埠期末)如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=5cm,AC=3cm,BC=4cm,则△DEB的周长为 .
13.(2019秋?无为县期末)如图,在一张直角三角形纸片ABC中,∠ACB=90°,∠A=30°P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP,当△A1CP与△ABC的重叠部分为等腰三角形时,则∠ACP的度数为 .
14.(2019秋?蚌埠期末)如图,等腰三角形底边BC的长为6,面积是24,腰AB的垂直平分线EF交AC于点F,D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为 .
15.(2019秋?肥西县期末)如图,△ABC中,∠ACB=90°,AC<BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B= .
16.(2019秋?肥西县期末)如图,在△ABC中,∠B=40°,∠C=45°,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,则∠DAE= .
17.(2019秋?颍州区期末)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+12∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是 .(填序号)
18.(2019秋?蜀山区期末)如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线.若BD=6,则CD= .
19.(2019秋?宣城期末)如图,在△ABC中,AB=AC,∠A=120°,BC=6cm,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,则MN的长为 cm.
20.(2019秋?濉溪县期末)如图,在△ABC中,BI、CI分别平分∠ABC、∠ACF,DE过点I,且DE∥BC.BD=8cm,CE=5cm,则DE等于 .
21.(2019秋?芜湖期末)如图,在△ABC中,∠ACB=90°,AB的垂直平分线DE交AB于E,交AC于D,∠DBC=30°,BD=4.6,则D到AB的距离为 .
22.(2019秋?芜湖期末)如图所示,△BDC′是将长方形纸牌ABCD沿着BD折叠得到的,图中(包括实线、虚线在内)共有全等三角形 对.
23.(2018秋?庐江县期末)如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=12EC中,正确的是 .
24.(2018秋?临泉县期末)如图,直线l1∥l2△ABC是等边三角形,若∠1=40°,则∠2的度数 .
25.(2018秋?临泉县期末)如图,等腰△ABC的底边BC长为2,面积是4,腰AC的垂直平分线EF分别交AC、AB于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△CDM的周长最小值为 .
2020-2021学年安徽省八年级上册数学(沪科版)期末考试复习:第15章《轴对称图形与等腰三角形》填空题精选
参考答案与试题解析
一.填空题(共25小题)
1.【解答】解:∵BO平分∠ABC,CO平分∠ACB,
∴∠DBO=∠OBC,∠ECO=∠BCO,
∵DE∥BC,
∴∠DOB=∠OBC,∠COE=∠OCB,
∴∠DOB=∠DBO,∠EOC=∠OCE,
∴BD=DO,OE=CE,
∴△ADE的周长=AD+DO+OE+AE=AD+DB+AE+EC=AB+AC
故答案为:AB+AC.
2.【解答】解:∵MN是线段AB的垂直平分线,
∴NA=NB,
∴AC=NA+NC=NB+NC=5,
∵△BCN的周长是8,
∴NB+NC+BC=8,
∴BC=8﹣5=3(cm),
故答案为:3cm.
3.【解答】解:作DF⊥AB于F,
∵BD平分∠ABC,DE⊥BC,DF⊥AB,
∴DE=DF,
∴12×AB×DF+12×BC×DE=S△ABC,即12×5×DE+12×7×DE=12,
解得,DE=2,
故答案为:2.
4.【解答】解:∵2x+y=14,
∴y=14﹣2x,即x<7,
∵两边之和大于第三边
∴x>72,
综上可得72<x<7
故答案为:y=﹣2x+14,72<x<7.
5.【解答】解:作PE⊥OB于E,如图,
∵OP平分∠AOB,PD⊥OA,PE⊥OB,
∴PE=PD=2,
∵OP平分∠AOB,
∴∠AOB=2∠AOP=2×15°=30°,
∵PC∥OA,
∴∠ECP=∠AOB=30°,
∴PC=2PE=4.
故答案为4.
6.【解答】解:∵D是AB的中点,CD⊥AB,
∴CD是线段AB 的垂直平分线,
∴CA=CB,
∴∠B=∠A=45°,
故答案为:45°.
7.【解答】解:设D到AB的距离为h,
∵∠C=90°,
∴DC⊥AC,
∵AD平分∠CAB,DC=3cm,
∴h=DC=3cm,
故答案为:3.
8.【解答】解:∵△ABC是等边三角形,AD⊥BC,
∴∠DAC=30°.
∵EF∥AC,
∴∠AGF=∠DAC=30°,故①正确,
∵EG∥AC,DE=EC,
∴AG=DG,故②正确,
∵AD=3BD,
∴BD≠DG,故③错误,
设AC=a,
∵∠DAC=30°,
∴AD=AC?cos30°=32a;
∵点G为AD的中点,
∴GE是△ADC的中位线,
∴点E时CD的中点,
∴EF=34AC=34a,
∵EF=34AC=34a,GE=12AC=12a,
∴EG=2FG,故④正确.
故答案为①②④.
9.【解答】解:∵AB的垂直平分线交AB于点D,
∴EA=EB,
∴△BCE的周长=EB+EC+BC=EA+EC+BC=AC+BC=15+8=23.
故答案为23.
10.【解答】解:∵△ABC和△A′B′C′关于MN对称,
∴得出△ABC≌△A′B′C′,
∴AC=A′C′,
∵AB﹣BC<AC<AB+BC,
∴6﹣3<AC<6+3
∴A′C′的取值范围是:3<A′C′<9.
故答案为:3<A′C′<9.
11.【解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=60°,
∵BD平分∠ABC,
∴∠CBD=12∠ABC=30°,
在Rt△BCD中,CD=12BD=12×10cm=5cm,
∵∠ABC的平分线BD交AC于点D,
∴点D到AB的距离为5cm.
故答案为5cm.
12.【解答】解:∵AD平分∠CAB交BC于D,DE⊥AB,DC⊥AC,
∴DC=DE,
在Rt△ADC和△ADE中
AD=ADDC=DE,
∴Rt△ADC≌△ADE(HL),
∴AE=AC=3,
∴BE=AB=5﹣3=2,
∴△DEB的周长=BE+BD+DE=BE+BD+CD=BE+BC=2+4=6(cm).
故答案为6cm.
13.【解答】解:当PC=CE时,如图1所示:
设∠ACP=x,则∠A1CP=x,
∵CP=CE,
∴∠CPE=∠CEP,
∵∠CPE=∠ACP+∠A=x+30°,
∴x+x+30°+x+30°=180°,
∴x=40°;
当CP=CE时,如图2所示:
设∠ACP=x.
则∠CPE=∠CEP=2x﹣90°+30°=2x﹣60°,
在△CPE中,90°﹣x+2(2x﹣60°)=180°,
解得:x=70°,
PE=PC不成立(因为∠CPE=x+30°>x,此时求得x=50°,点E应该在AB延长线上),
综上所述,∠ACP的度数为40°或70°,
故答案为:40°或70°.
14.【解答】解:∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×6×AD=24,解得AD=8,
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+12BC=8+12×6=8+3=11.
故答案为11.
15.【解答】解:∵△CDF中,∠C=90°,且△CDF是等腰三角形,
∴CF=CD,
∴∠CFD=∠CDF=45°,
设∠DAE=x°,由对称性可知,AF=FD,AE=DE,
∴∠FDA=12∠CFD=22.5°,∠DEB=2x°,
分类如下:
①当DE=DB时,如图1所示:
∠B=∠DEB=2x°,
由∠CDE=∠DEB+∠B,得45°+22.5°+x=4x,
解得:x=22.5°.
此时∠B=2x=45°,
∵AC<BC,
∴∠B=45°不成立;
②当BD=BE时,如图2所示:
则∠B=(180°﹣4x)°,∠CAB=60°,∠CAD=22.5°.
由∠CDE=∠DEB+∠B得:45°+22.5°+x=2x+180°﹣4x,
解得x=37.5°,
此时∠B=(180﹣4x)°=30°.
图形(2)说明:∠CAB=60°,∠CAD=22.5°.
③DE=BE时,则∠B=12(180﹣2x)°,
由∠CDE=∠DEB+∠B得,45°+22.5°+x=2x+12(180﹣2x)°,
此方程无解.
∴DE=BE不成立.
综上所述,∠B=30°.
故答案为:30°.
16.【解答】解:∵点D、E分别是AB、AC边的垂直平分线与BC的交点,
∴AD=BD,AE=CE,
∴∠B=∠BAD,∠C=∠CAE,
∵∠B=40°,∠C=45°,
∴∠B+∠C=85°,∠BAC=95°,
∴∠BAD+∠CAE=85°,
∴∠DAE=∠BAC﹣(∠BAD+∠CAE)=95°﹣85°=10°,
故答案为:10°
17.【解答】解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=12∠ABC,∠OCB=12∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-12∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+12∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=12AE?OM+12AF?OD=12OD?(AE+AF)=12mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故答案是:①②③
18.【解答】解:∵∠C=90°,∠A=30°,
∴∠ABC=180°﹣30°﹣90°=60°,
∵BD是∠ABC的平分线,
∴∠DBC=12∠ABC=30°,
∵∠C=90°,
∴CD=12BD=12×6=3,
故答案为:3.
19.【解答】解:连接AN、AM,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵EM是AB的垂直平分线,
∴MB=MA,
∴∠MAB=∠B=30°,
∴∠NMA=60°,
同理NA=NC,∠MNA=60°,
∴△MAN是等边三角形,
∴BM=MN=NC=13BC=2cm,
故答案为:2.
20.【解答】解:∵BI、CI分别平分∠ABC、∠ACF,
∴∠ABI=∠CBI,∠ECI=∠ICF,
∵DE∥BC,
∴∠DIB=∠CBI,∠EIC=∠ICF,
∴∠ABI=∠DIB,∠ECI=∠EIC,
∴DI=BD=8cm,EI=CE=5cm,
∴DE=DI﹣EI=3(cm).
故答案为:3cm.
21.【解答】解:∵DE垂直平分AB,
∴DB=DA,
∴∠A=∠ABD,
∵∠C=90°,∠DBC=30°,
∴∠A+∠ABD=90°﹣30°=60°,
∴∠ABD=30°,
在Rt△BED中,∠EBD=30°,BD=4.6,
∴DE=12BD=2.3,
即D到AB的距离为2.3.
故答案为2.3.
22.【解答】∵四边形ABCD是长方形,
∴∠A=∠C=90°,AB=CD,AD=BC,
∴△ABD≌△CDB.(HL)
∵△BDC是将长方形纸牌ABCD沿着BD折叠得到的,
∴BC′=AD,BD=BD,∠C′=∠A.
∴△ABD≌△C′DB.(HL)
同理△DCB≌△C′DB.
∵∠A=∠C′,∠AOB=∠C′OD,AB=C′D,
∴△AOB≌△C′OD.(AAS)
所以共有四对全等三角形.
23.【解答】解:∵△ABC是等边三角形,
∴AB=AC,∠B=∠BAC=∠ACE=60°,
在△ABD和△ACE中,AB=AC∠B=∠ACEBD=CE,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE,AD=AE,故①正确;
由折叠的性质得:CE=CM=BD,AE=AM=AD,∠CAE=∠CAM=∠BAD,
∴∠DAM=∠BAC=60°,
∴△ADM是等边三角形,
∴DM=AD,
∵AB>AD,
∴AB>DM,
∵∠ACD>∠DAC,
∴AD>DC,
∴△ABD与△DCM不全等,故③正确、②错误;
由折叠的性质得:AE=AM,CE=CM,
∴AC垂直平分EM,
∴∠ENC=90°,
∵∠ACE=60°,
∴∠CEN=30°,
∴CN=12EC,故④正确,
故答案为:①③④.
24.【解答】解:如图,
∵△ABC是等边三角形,
∴∠C=60°,
∵∠1=40°,
∴∠3=40°+60°=100°,
∵直线l1∥l2,
∴∠2=∠3=100°,
故答案为:100°.
25.【解答】解:连接AM、连接AD交EF与点M′.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=12BC?AD=12×2×AD=4,解得AD=4,
∵EF是线段AB的垂直平分线,
∴AM=CM.
∴CM+MD=AM+MD.
∴当点M位于点M′处时,AM+MD有最小值,最小值即为AD=4.
∴△CDM的周长的最小值为CM+MD+CD=AD+CD=4+1=5.
故答案为5.
