鲁教版(五四制)2020年七年级上册期末复习(word版,含答案)
文档属性
| 名称 | 鲁教版(五四制)2020年七年级上册期末复习(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 611.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览



文档简介
七上期末考试复习指导课
一、考试范围、分值及难度
期末考试考察的范围为七年级上册全部内容
分值:150分(120分钟)
难度:中等难度
二、常考题型大阅兵
1、三角形基础知识的考察
【考点解析】
三角形基础知识的考察主要围绕内角和、三线、三边关系、特殊三角形(等腰、等边、直角、等腰直角三角形)的性质来进行考察,并且结合第二章的中垂线、角平分线性质来进行考察,全等三角形的判定也会有所涉及,需要熟练掌握几种判定方法ASA、AAS、SAS、SSS,以及不能判定三角形的全等的条件AAA、SSA。
【题型回放】
(1)下列长度的三根木棒首尾相接,不能做成三角形框架的是(
)
A.4cm,7cm,3cm
B.7cm,3cm,8cm
C.5cm,6cm,7cm
D.2cm,4cm,5cm
(第2题)
(第4题)
(第5题)
(第6题)
(2)如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是(
)
A.AB=CD
B.AC=BD
C.∠A=∠D
D.∠ABC=∠DCB
(3)一个等腰三角形的两边长分别为4,8,则它的周长为(
)
A.12
B.16
C.
20
D.16或20
(4)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC=(
)
A.
B.2
C.3
D.+2
(5)如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为(
)
A.3cm
B.6cm
C.12cm
D.16cm
(6)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF//AC交ED的延长线于点F,若
BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有(
)
A.4
B.3
C.2
D.1
(7)如图,AD,CE是△ABC的两条高,已知AD=10,CE=9,AB=12,则
BC的长是(
)
A.10
B.10.8
C.12
D.15
(8)如图,在△ABC中,∠B,∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=(
)
A.110°
B.120°
C.130°
D.140°
(9)将一副三角尺如图叠放,则图中的度数为
。
(10)如图,△ABC三个内角的平分线交于点
O,点D在CA的延长线上,且DC=BC.若∠D=20°,则∠ABC的度数为
。
(第7题)
(第8题)
(第9题)
(第10题)
2、三角形综合题的考察
【考点解析】
三角形综合题的考察主要围绕证明和计算两大部分来进行,需要熟练掌握基本的定理,熟练运用并灵活掌握定理的使用条件。一般运用全等三角形作为解决题目的基本方法,同时结合中垂线、角平分、等腰三角形的三线合一进行综合考察。要熟练掌握基本的几何模型。
【题型回放】
(1)如图,四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC,求证:OA⊥OC
(2)如图,以等腰直角△ABC的直角边AC作等边△ACD,CE⊥AD于E,BD、CE交于点F.
①求∠DCB、∠DFE的度数;
②求证:△ADF是等腰直角三角形;
③求证:AB=2DF.
3、勾股定理相关知识的考察
【考点解析】
勾股定理的考察主要是围绕勾股数、直角三角形的判定、勾股定理的实际应用以及最短路径那个问题,同时还有结合折叠问题,利用方程思想来进行考察。综合题主要围绕计算线段长度和图形面积,以及证明直角三角形等方面进行考察。
【题型回放】
(1)下列各组数中的三个数值分别为三角形的三边长,不能构成直角三角形的是(
)
A.3、4、5
B.5、12、13
C.、2、
D.7、24、25
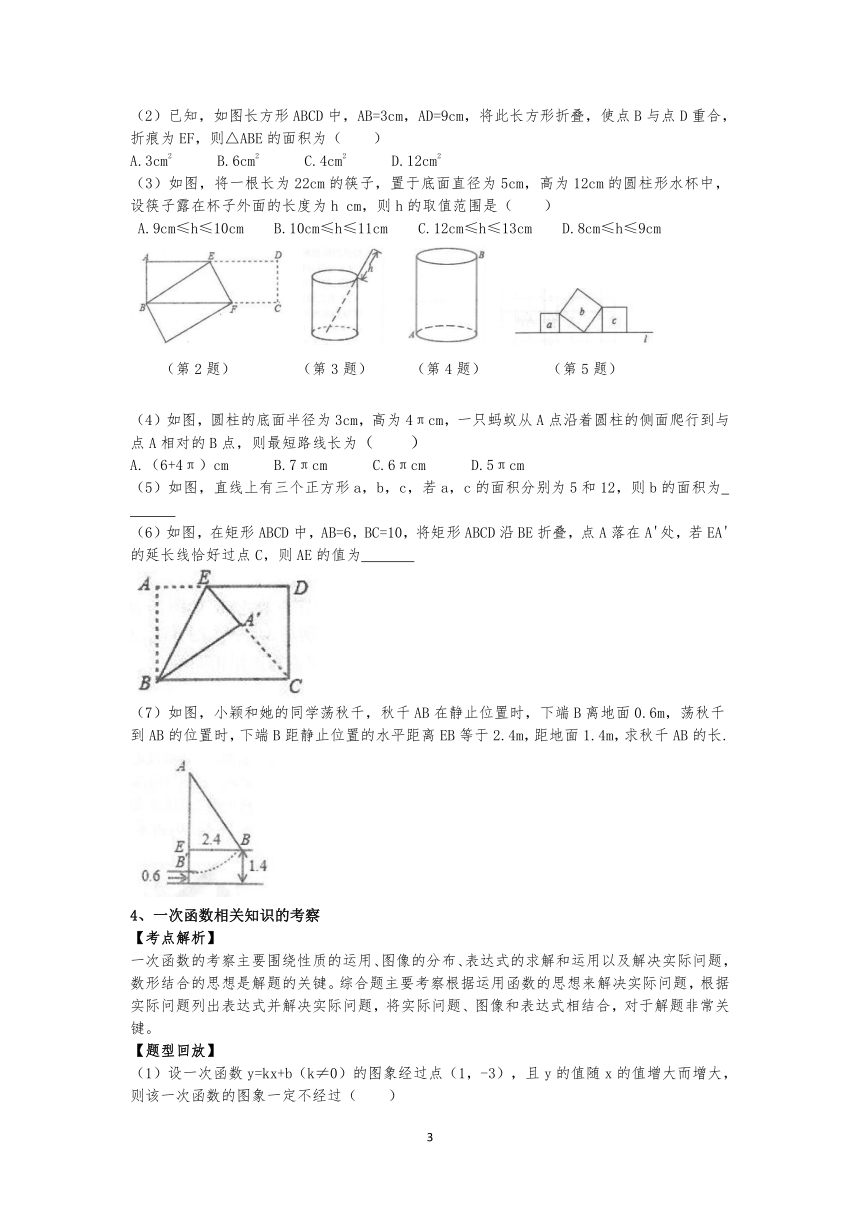
(2)已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为(
)
A.3cm2
B.6cm2
C.4cm2
D.12cm2
(3)如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为h
cm,则h的取值范围是(
)
A.9cm≤h≤10cm
B.10cm≤h≤11cm
C.12cm≤h≤13cm
D.8cm≤h≤9cm
(第2题)
(第3题)
(第4题)
(第5题)
(4)如图,圆柱的底面半径为3cm,高为4πcm,一只蚂蚁从A点沿着圆柱的侧面爬行到与点A相对的B点,则最短路线长为(
)
A.(6+4π)cm
B.7πcm
C.6πcm
D.5πcm
(5)如图,直线上有三个正方形a,b,c,若a,c的面积分别为5和12,则b的面积为
(6)如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA'的延长线恰好过点C,则AE的值为
(7)如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
4、一次函数相关知识的考察
【考点解析】
一次函数的考察主要围绕性质的运用、图像的分布、表达式的求解和运用以及解决实际问题,数形结合的思想是解题的关键。综合题主要考察根据运用函数的思想来解决实际问题,根据实际问题列出表达式并解决实际问题,将实际问题、图像和表达式相结合,对于解题非常关键。
【题型回放】
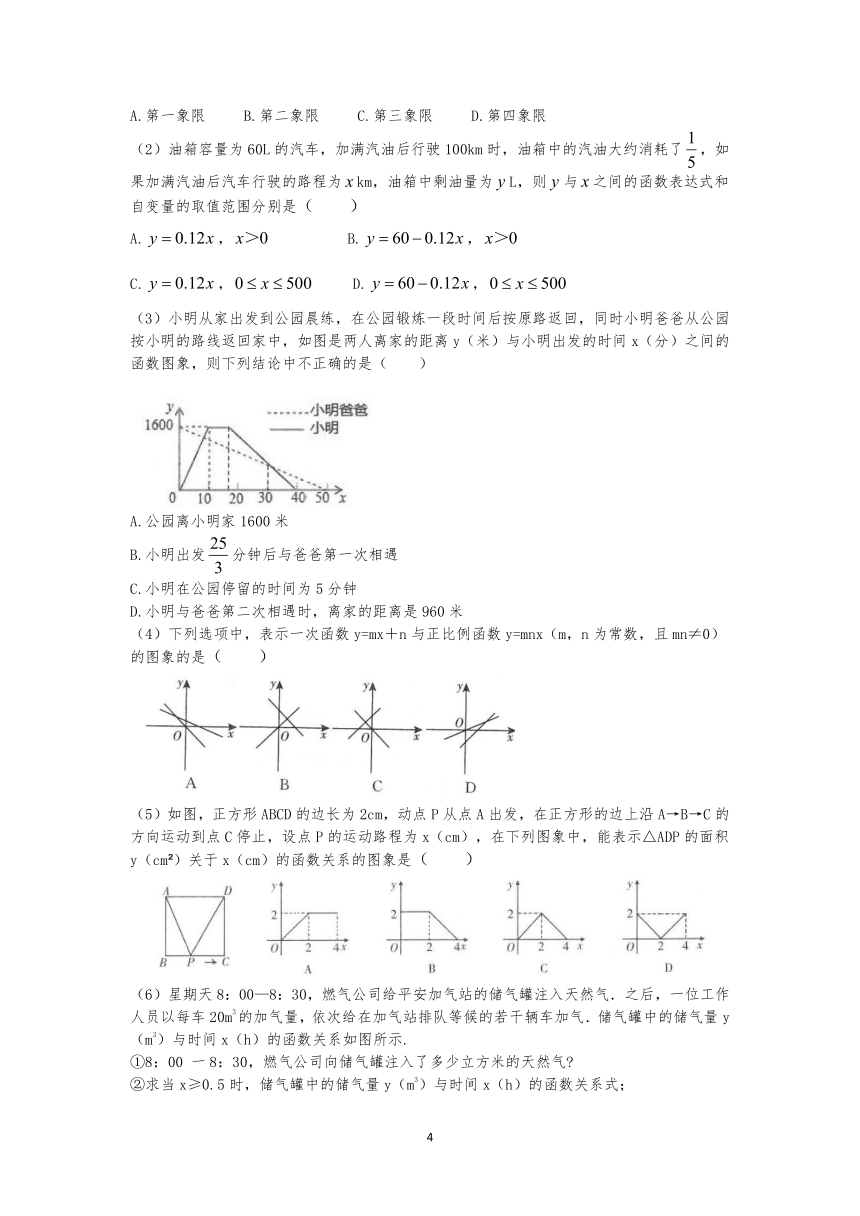
(1)设一次函数y=kx+b(k≠0)的图象经过点(1,-3),且y的值随x的值增大而增大,则该一次函数的图象一定不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
(2)油箱容量为60L的汽车,加满汽油后行驶100km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为km,油箱中剩油量为L,则与之间的函数表达式和自变量的取值范围分别是(
)
A.,
B.,
C.,
D.,
(3)小明从家出发到公园晨练,在公园锻炼一段时间后按原路返回,同时小明爸爸从公园按小明的路线返回家中,如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象,则下列结论中不正确的是(
)
A.公园离小明家1600米
B.小明出发分钟后与爸爸第一次相遇
C.小明在公园停留的时间为5分钟
D.小明与爸爸第二次相遇时,离家的距离是960米
(4)下列选项中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是(
)
(5)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm?)关于x(cm)的函数关系的图象是(
)
(6)星期天8:00—8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20m3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图所示.
①8:00
一8:30,燃气公司向储气罐注入了多少立方米的天然气?
②求当x≥0.5时,储气罐中的储气量y(m3)与时间x(h)的函数关系式;
③请判断:正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
(7)某班级计划暑假组织部分学生夏令营,估计人数在7~13人之间.甲、乙旅行社的服务质量相同,且对外报价都是300元/人,该班联系时,甲旅行社表示可给予每位学生八折优惠;乙旅行社表示,可先免去一位学生的夏令营费用,其余学生九折优惠.
①分别写出两旅行社所报夏令营费用y(元)与人数x(人)的函数表达式;
②若有11
人参加夏令营,选择哪个旅行社更划算?
③人数在什么范围内,选甲旅行社较划算?人数在什么范围内,选乙旅行社较划算?
(8)如图,点A的坐标为(,0),点B的坐标为(0,3).
①求过A,B两点直线的函数表达式;
②过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
5、轴对称、坐标系相关知识的考察
【考点解析】
轴对称的考察主要以选择题和填空题等客观题为主,题目较为简单,轴对称的性质需要熟练掌握,折叠问题需要作为重难点题型进行掌握。坐标系的考查主要是一些简单的题型,往往和对称结合进行考察。
【题型回放】
(1)下列“慢行通过、注意危险、禁止行人通行、禁止非机动车通行”四个交通标志图(黑白阴影图片)中为轴对称图形的是(
)
(2)如图,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠,使点A,D分别落在长方形ABCD外部的点A1D1处,则阴影部分图形的周长为(
)
A.15
B.20
C.25
D.30
(第2题)
(第3题)
(3)如图,△ABP和△DCP是两个全等的等边三角形,且PA⊥PD,有以下4个结论:①∠PBC=15°;②AD//BC;③直线PC⊥AB;④四边形ABCD是轴对称图形.其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
(4)已知点P1(a-1,3)和点P2(2,b-1)关于x轴对称,则的值是(
)
A.1
B.-2
C.2019
D.-2019
(5)在平面直角坐标系中,点(1,1)关于y轴对称的点的坐标是(
)
A.(-1,-1)
B.(1,-1)
C.(-1,1)
D.(1,1)
6、无理数、开方运算等相关知识的考察
【考点解析】
无理数的考察主要以选择题和填空题等客观题为主,题目较为简单,需要掌握清楚无理数的表现形式进行判断。实数范围内的运算也是期末考试必考内容。熟练掌握取绝对值符号的方法。
【题型回放】
(1)若2m-4与3m-1是同一个数的两个平方根,则m为(
)
A.
-3
B.1
C.-3或1
D.-1
(2)在实数:,,,,,,(相邻两个3之间7的个数逐次加1),,,无理数的个数为(
)
A.7个
B.6个
C.5个
D.4个
(3)下列四个数:0,,-π,1,其中最小的数是(
)
A.-π
B.0
C.1
D.
(4)计算:
①
②
参考答案
1、三角形基础知识的考察
1-8
AACCAABB
9、15°10、40°
2、三角形综合题的考察
(1)证明:过点O作OE⊥AC于E,
∵∠ABD=90°,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OB=OE,
∵在Rt△ABO和Rt△AEO
中,
A0=AO
OB=OE
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOB+∠COE=90°
∴
OA⊥OC
(2)①∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=60°+90°=150°,
∵BC=CD
∴∠BDC=(180°-150°)=15°,
∴∠ADF=60°-15°=
45°,
∴∠DFE=180°-∠DEF-∠EDF=45°
②∵△ACD是等边三角形,CE⊥AD,
∴CE垂直平分AD
∴DF=AF
∵∠ADF=45°,∴∠DAF=45°,∠AFD=90°,
∴△ADF是等腰直角三角形;
③∵△ABC是等腰三角形,
∴∠CAB=∠CBA=45°
∴∠ABF=45°-15°=30°
所以AB=2AF=2DF
3、勾股定理相关知识的考察
1-4
CBAD
5、17
6、2
7、设AB=AB’=x,由题意可得出:
B’E=1.4-0.6=0.8(m),
则AE=AB-0.8,
在Rt△AEB中,∵AE2+BE2=AB2,
∴(x-0.8)2+2.42=x2
解得x=4,
答:秋千AB的长为4m.
4、一次函数相关知识的考察
1-5
BDDAA
6.(1)解:由题意得,8:00—8:30,燃气公司向储气罐注入了10000-2000=
8000(立方米),
即8:00—8:30,燃气公司向储气罐注入了8000立方米的天然气;
(2)当x≥0.5
时,设函数关系式为
k=-200解得,
即当x≥
0.5
时,储气罐中的储气量y(m3)与时间x(h)的函数关系式是
(3)能。
理由:18辆汽车需加气18×20=360(m3),
加完气后储气量为10000-360=
9640(m3)
解得,,
∴2.3-0.5=1.8(h),
而8:30
到10:30相差2h,
∴能加完气。
7.(1)对甲旅社,;
对乙旅社,;
(2)若选择甲旅行社,
若选择乙旅行社,
∴应选甲旅行社。
若选甲旅行社,则令,即,解得:
若选甲旅行社,则令,即,解得:
当时,,即所需费用一样。
所以,当人数为9人时,选两家旅行都是一样。当人数少于9人时,应选乙旅行社;当人数多于9人时,应选甲旅行社。
8.(1)设过A,B两点的直线解析式为,则根据题意,得
则过A,B两点的直线解析式为
(2)设P点坐标为(x,0),依据题意得,所有P点坐标分别为(3,0)或(-3,0)
S△ABP的面积为或
5、轴对称、坐标系相关知识的考察
1-5
BDDCA
6、无理数、开方运算等相关知识的考察
1-3
BDA
4(1)-12.5(2)4
一、考试范围、分值及难度
期末考试考察的范围为七年级上册全部内容
分值:150分(120分钟)
难度:中等难度
二、常考题型大阅兵
1、三角形基础知识的考察
【考点解析】
三角形基础知识的考察主要围绕内角和、三线、三边关系、特殊三角形(等腰、等边、直角、等腰直角三角形)的性质来进行考察,并且结合第二章的中垂线、角平分线性质来进行考察,全等三角形的判定也会有所涉及,需要熟练掌握几种判定方法ASA、AAS、SAS、SSS,以及不能判定三角形的全等的条件AAA、SSA。
【题型回放】
(1)下列长度的三根木棒首尾相接,不能做成三角形框架的是(
)
A.4cm,7cm,3cm
B.7cm,3cm,8cm
C.5cm,6cm,7cm
D.2cm,4cm,5cm
(第2题)
(第4题)
(第5题)
(第6题)
(2)如图,已知∠1=∠2,则下列条件中,不能使△ABC≌△DCB成立的是(
)
A.AB=CD
B.AC=BD
C.∠A=∠D
D.∠ABC=∠DCB
(3)一个等腰三角形的两边长分别为4,8,则它的周长为(
)
A.12
B.16
C.
20
D.16或20
(4)如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,DE=1,则BC=(
)
A.
B.2
C.3
D.+2
(5)如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm,△ABD的周长为13cm,则AE的长为(
)
A.3cm
B.6cm
C.12cm
D.16cm
(6)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF//AC交ED的延长线于点F,若
BC恰好平分∠ABF,AE=2BF.给出下列四个结论:
①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有(
)
A.4
B.3
C.2
D.1
(7)如图,AD,CE是△ABC的两条高,已知AD=10,CE=9,AB=12,则
BC的长是(
)
A.10
B.10.8
C.12
D.15
(8)如图,在△ABC中,∠B,∠C的平分线BE,CD相交于点F,∠A=60°,则∠BFC=(
)
A.110°
B.120°
C.130°
D.140°
(9)将一副三角尺如图叠放,则图中的度数为
。
(10)如图,△ABC三个内角的平分线交于点
O,点D在CA的延长线上,且DC=BC.若∠D=20°,则∠ABC的度数为
。
(第7题)
(第8题)
(第9题)
(第10题)
2、三角形综合题的考察
【考点解析】
三角形综合题的考察主要围绕证明和计算两大部分来进行,需要熟练掌握基本的定理,熟练运用并灵活掌握定理的使用条件。一般运用全等三角形作为解决题目的基本方法,同时结合中垂线、角平分、等腰三角形的三线合一进行综合考察。要熟练掌握基本的几何模型。
【题型回放】
(1)如图,四边形ABDC中,∠D=∠B=90°,点O为BD的中点,且AO平分∠BAC,求证:OA⊥OC
(2)如图,以等腰直角△ABC的直角边AC作等边△ACD,CE⊥AD于E,BD、CE交于点F.
①求∠DCB、∠DFE的度数;
②求证:△ADF是等腰直角三角形;
③求证:AB=2DF.
3、勾股定理相关知识的考察
【考点解析】
勾股定理的考察主要是围绕勾股数、直角三角形的判定、勾股定理的实际应用以及最短路径那个问题,同时还有结合折叠问题,利用方程思想来进行考察。综合题主要围绕计算线段长度和图形面积,以及证明直角三角形等方面进行考察。
【题型回放】
(1)下列各组数中的三个数值分别为三角形的三边长,不能构成直角三角形的是(
)
A.3、4、5
B.5、12、13
C.、2、
D.7、24、25
(2)已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为(
)
A.3cm2
B.6cm2
C.4cm2
D.12cm2
(3)如图,将一根长为22cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,设筷子露在杯子外面的长度为h
cm,则h的取值范围是(
)
A.9cm≤h≤10cm
B.10cm≤h≤11cm
C.12cm≤h≤13cm
D.8cm≤h≤9cm
(第2题)
(第3题)
(第4题)
(第5题)
(4)如图,圆柱的底面半径为3cm,高为4πcm,一只蚂蚁从A点沿着圆柱的侧面爬行到与点A相对的B点,则最短路线长为(
)
A.(6+4π)cm
B.7πcm
C.6πcm
D.5πcm
(5)如图,直线上有三个正方形a,b,c,若a,c的面积分别为5和12,则b的面积为
(6)如图,在矩形ABCD中,AB=6,BC=10,将矩形ABCD沿BE折叠,点A落在A'处,若EA'的延长线恰好过点C,则AE的值为
(7)如图,小颖和她的同学荡秋千,秋千AB在静止位置时,下端B离地面0.6m,荡秋千到AB的位置时,下端B距静止位置的水平距离EB等于2.4m,距地面1.4m,求秋千AB的长.
4、一次函数相关知识的考察
【考点解析】
一次函数的考察主要围绕性质的运用、图像的分布、表达式的求解和运用以及解决实际问题,数形结合的思想是解题的关键。综合题主要考察根据运用函数的思想来解决实际问题,根据实际问题列出表达式并解决实际问题,将实际问题、图像和表达式相结合,对于解题非常关键。
【题型回放】
(1)设一次函数y=kx+b(k≠0)的图象经过点(1,-3),且y的值随x的值增大而增大,则该一次函数的图象一定不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
(2)油箱容量为60L的汽车,加满汽油后行驶100km时,油箱中的汽油大约消耗了,如果加满汽油后汽车行驶的路程为km,油箱中剩油量为L,则与之间的函数表达式和自变量的取值范围分别是(
)
A.,
B.,
C.,
D.,
(3)小明从家出发到公园晨练,在公园锻炼一段时间后按原路返回,同时小明爸爸从公园按小明的路线返回家中,如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象,则下列结论中不正确的是(
)
A.公园离小明家1600米
B.小明出发分钟后与爸爸第一次相遇
C.小明在公园停留的时间为5分钟
D.小明与爸爸第二次相遇时,离家的距离是960米
(4)下列选项中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是(
)
(5)如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm?)关于x(cm)的函数关系的图象是(
)
(6)星期天8:00—8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20m3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图所示.
①8:00
一8:30,燃气公司向储气罐注入了多少立方米的天然气?
②求当x≥0.5时,储气罐中的储气量y(m3)与时间x(h)的函数关系式;
③请判断:正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
(7)某班级计划暑假组织部分学生夏令营,估计人数在7~13人之间.甲、乙旅行社的服务质量相同,且对外报价都是300元/人,该班联系时,甲旅行社表示可给予每位学生八折优惠;乙旅行社表示,可先免去一位学生的夏令营费用,其余学生九折优惠.
①分别写出两旅行社所报夏令营费用y(元)与人数x(人)的函数表达式;
②若有11
人参加夏令营,选择哪个旅行社更划算?
③人数在什么范围内,选甲旅行社较划算?人数在什么范围内,选乙旅行社较划算?
(8)如图,点A的坐标为(,0),点B的坐标为(0,3).
①求过A,B两点直线的函数表达式;
②过B点作直线BP与x轴交于点P,且使OP=2OA,求△ABP的面积.
5、轴对称、坐标系相关知识的考察
【考点解析】
轴对称的考察主要以选择题和填空题等客观题为主,题目较为简单,轴对称的性质需要熟练掌握,折叠问题需要作为重难点题型进行掌握。坐标系的考查主要是一些简单的题型,往往和对称结合进行考察。
【题型回放】
(1)下列“慢行通过、注意危险、禁止行人通行、禁止非机动车通行”四个交通标志图(黑白阴影图片)中为轴对称图形的是(
)
(2)如图,在长方形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将长方形ABCD沿EF折叠,使点A,D分别落在长方形ABCD外部的点A1D1处,则阴影部分图形的周长为(
)
A.15
B.20
C.25
D.30
(第2题)
(第3题)
(3)如图,△ABP和△DCP是两个全等的等边三角形,且PA⊥PD,有以下4个结论:①∠PBC=15°;②AD//BC;③直线PC⊥AB;④四边形ABCD是轴对称图形.其中正确的结论有(
)
A.1个
B.2个
C.3个
D.4个
(4)已知点P1(a-1,3)和点P2(2,b-1)关于x轴对称,则的值是(
)
A.1
B.-2
C.2019
D.-2019
(5)在平面直角坐标系中,点(1,1)关于y轴对称的点的坐标是(
)
A.(-1,-1)
B.(1,-1)
C.(-1,1)
D.(1,1)
6、无理数、开方运算等相关知识的考察
【考点解析】
无理数的考察主要以选择题和填空题等客观题为主,题目较为简单,需要掌握清楚无理数的表现形式进行判断。实数范围内的运算也是期末考试必考内容。熟练掌握取绝对值符号的方法。
【题型回放】
(1)若2m-4与3m-1是同一个数的两个平方根,则m为(
)
A.
-3
B.1
C.-3或1
D.-1
(2)在实数:,,,,,,(相邻两个3之间7的个数逐次加1),,,无理数的个数为(
)
A.7个
B.6个
C.5个
D.4个
(3)下列四个数:0,,-π,1,其中最小的数是(
)
A.-π
B.0
C.1
D.
(4)计算:
①
②
参考答案
1、三角形基础知识的考察
1-8
AACCAABB
9、15°10、40°
2、三角形综合题的考察
(1)证明:过点O作OE⊥AC于E,
∵∠ABD=90°,OA平分∠BAC,
∴OB=OE,
∵点O为BD的中点,
∴OB=OD,
∴OE=OD,
∴OB=OE,
∵在Rt△ABO和Rt△AEO
中,
A0=AO
OB=OE
∴Rt△ABO≌Rt△AEO(HL),
∴∠AOB=∠AOE,
同理求出∠COD=∠COE,
∴∠AOC=∠AOB+∠COE=90°
∴
OA⊥OC
(2)①∵△ACD是等边三角形,
∴∠ACD=60°,
∴∠BCD=60°+90°=150°,
∵BC=CD
∴∠BDC=(180°-150°)=15°,
∴∠ADF=60°-15°=
45°,
∴∠DFE=180°-∠DEF-∠EDF=45°
②∵△ACD是等边三角形,CE⊥AD,
∴CE垂直平分AD
∴DF=AF
∵∠ADF=45°,∴∠DAF=45°,∠AFD=90°,
∴△ADF是等腰直角三角形;
③∵△ABC是等腰三角形,
∴∠CAB=∠CBA=45°
∴∠ABF=45°-15°=30°
所以AB=2AF=2DF
3、勾股定理相关知识的考察
1-4
CBAD
5、17
6、2
7、设AB=AB’=x,由题意可得出:
B’E=1.4-0.6=0.8(m),
则AE=AB-0.8,
在Rt△AEB中,∵AE2+BE2=AB2,
∴(x-0.8)2+2.42=x2
解得x=4,
答:秋千AB的长为4m.
4、一次函数相关知识的考察
1-5
BDDAA
6.(1)解:由题意得,8:00—8:30,燃气公司向储气罐注入了10000-2000=
8000(立方米),
即8:00—8:30,燃气公司向储气罐注入了8000立方米的天然气;
(2)当x≥0.5
时,设函数关系式为
k=-200解得,
即当x≥
0.5
时,储气罐中的储气量y(m3)与时间x(h)的函数关系式是
(3)能。
理由:18辆汽车需加气18×20=360(m3),
加完气后储气量为10000-360=
9640(m3)
解得,,
∴2.3-0.5=1.8(h),
而8:30
到10:30相差2h,
∴能加完气。
7.(1)对甲旅社,;
对乙旅社,;
(2)若选择甲旅行社,
若选择乙旅行社,
∴应选甲旅行社。
若选甲旅行社,则令,即,解得:
若选甲旅行社,则令,即,解得:
当时,,即所需费用一样。
所以,当人数为9人时,选两家旅行都是一样。当人数少于9人时,应选乙旅行社;当人数多于9人时,应选甲旅行社。
8.(1)设过A,B两点的直线解析式为,则根据题意,得
则过A,B两点的直线解析式为
(2)设P点坐标为(x,0),依据题意得,所有P点坐标分别为(3,0)或(-3,0)
S△ABP的面积为或
5、轴对称、坐标系相关知识的考察
1-5
BDDCA
6、无理数、开方运算等相关知识的考察
1-3
BDA
4(1)-12.5(2)4
同课章节目录
