2020-2021学年安徽省合肥九年级(上)第一次月考数学试卷(Word版含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥九年级(上)第一次月考数学试卷(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 131.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 08:31:52 | ||
图片预览

文档简介
2020-2021学年安徽省合肥九年级(上)第一次月考数学试卷
题号
一
二
三
四
总分
得分
一、选择题(本大题共10小题,共40.0分)
函数图象顶点坐标是
A.
B.
C.
D.
若将抛物线先向右平移2个单位,再向上平移1个单位,得到的新抛物线的表达式为???
A.
B.
C.
D.
下列四组线段中,能构成比例线段的一组是
A.
1cm,3cm,3cm,6cm
B.
2cm,3cm,4cm,6cm
C.
4cm,5m,6cm,
D.
1cm,,3cm,
已知x:y::4:6,则的值为
A.
B.
1
C.
D.
已知点P是线段AB的一个黄金分割点,且,,则PA的长是
A.
B.
C.
D.
在反比例函数图象上有两点,B?,,,则m的取值范围是
A.
B.
C.
D.
如图为二次函数的图象,下列各式中:,,,,正确的只有
A.
B.
C.
D.
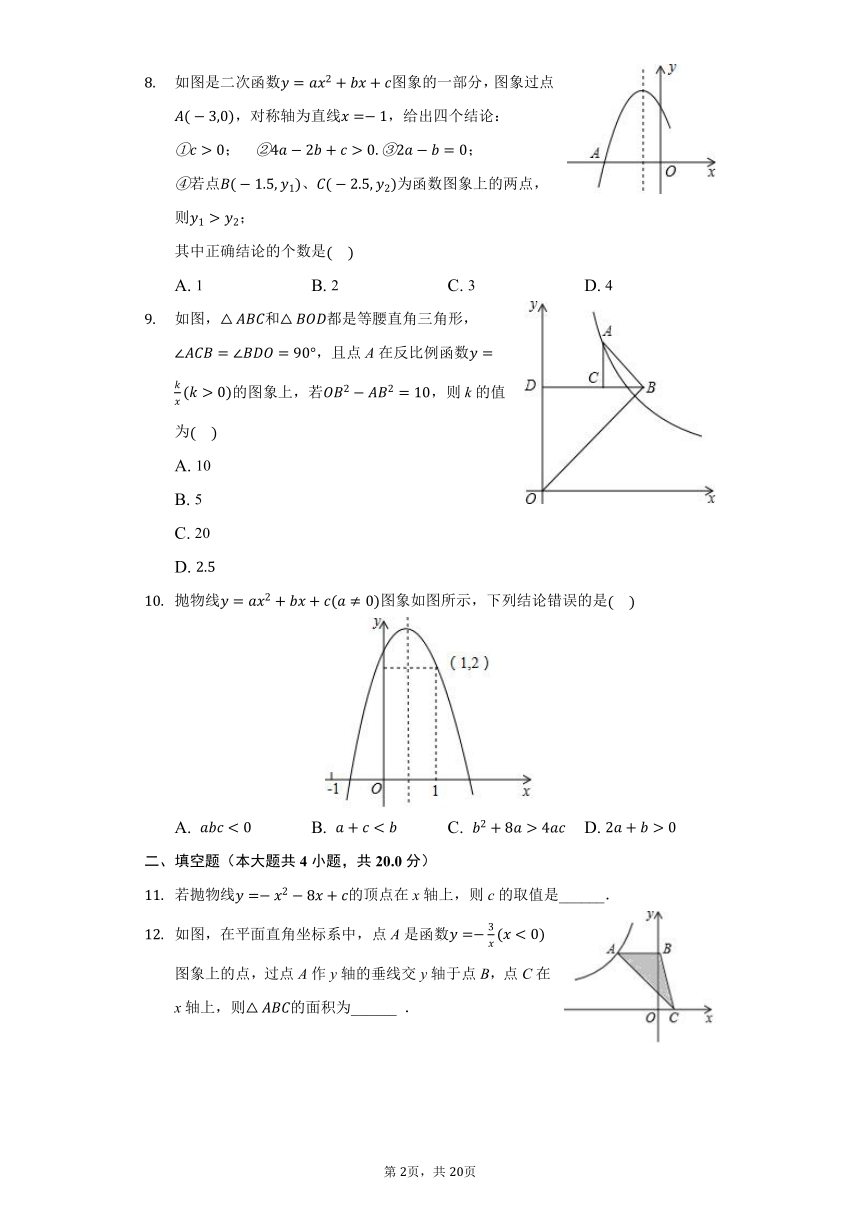
如图是二次函数图象的一部分,图象过点,对称轴为直线,给出四个结论:
;????;
若点、为函数图象上的两点,则;
其中正确结论的个数是
A.
1
B.
2
C.
3
D.
4
如图,和都是等腰直角三角形,,且点A在反比例函数的图象上,若,则k的值为
A.
10
B.
5
C.
20
D.
抛物线图象如图所示,下列结论错误的是
A.
B.
C.
D.
二、填空题(本大题共4小题,共20.0分)
若抛物线的顶点在x轴上,则c的取值是______.
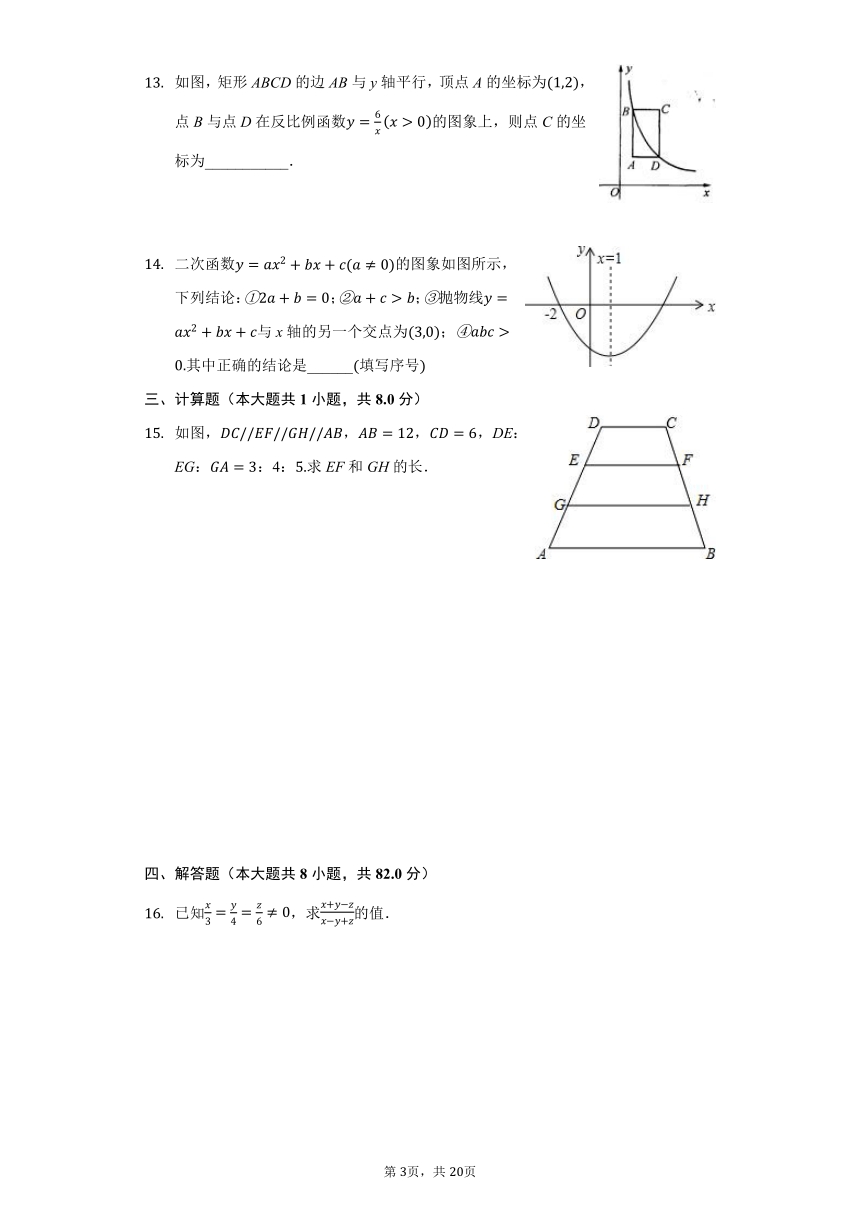
如图,在平面直角坐标系中,点A是函数图象上的点,过点A作y轴的垂线交y轴于点B,点C在x轴上,则的面积为______
.
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为,点B与点D在反比例函数的图象上,则点C的坐标为___________.
二次函数的图象如图所示,下列结论:;;抛物线与x轴的另一个交点为;其中正确的结论是______填写序号
三、计算题(本大题共1小题,共8.0分)
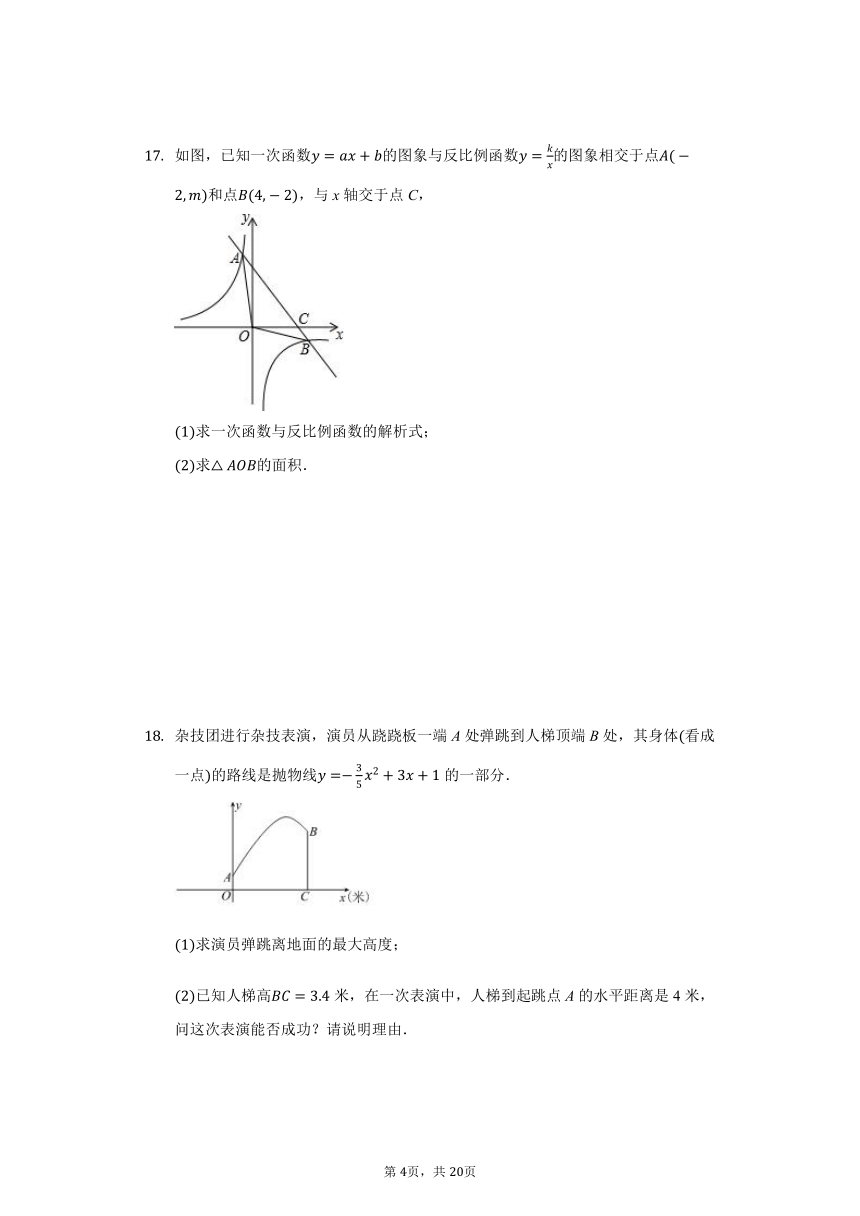
如图,,,,DE:EG::4:求EF和GH的长.
四、解答题(本大题共8小题,共82.0分)
已知,求的值.
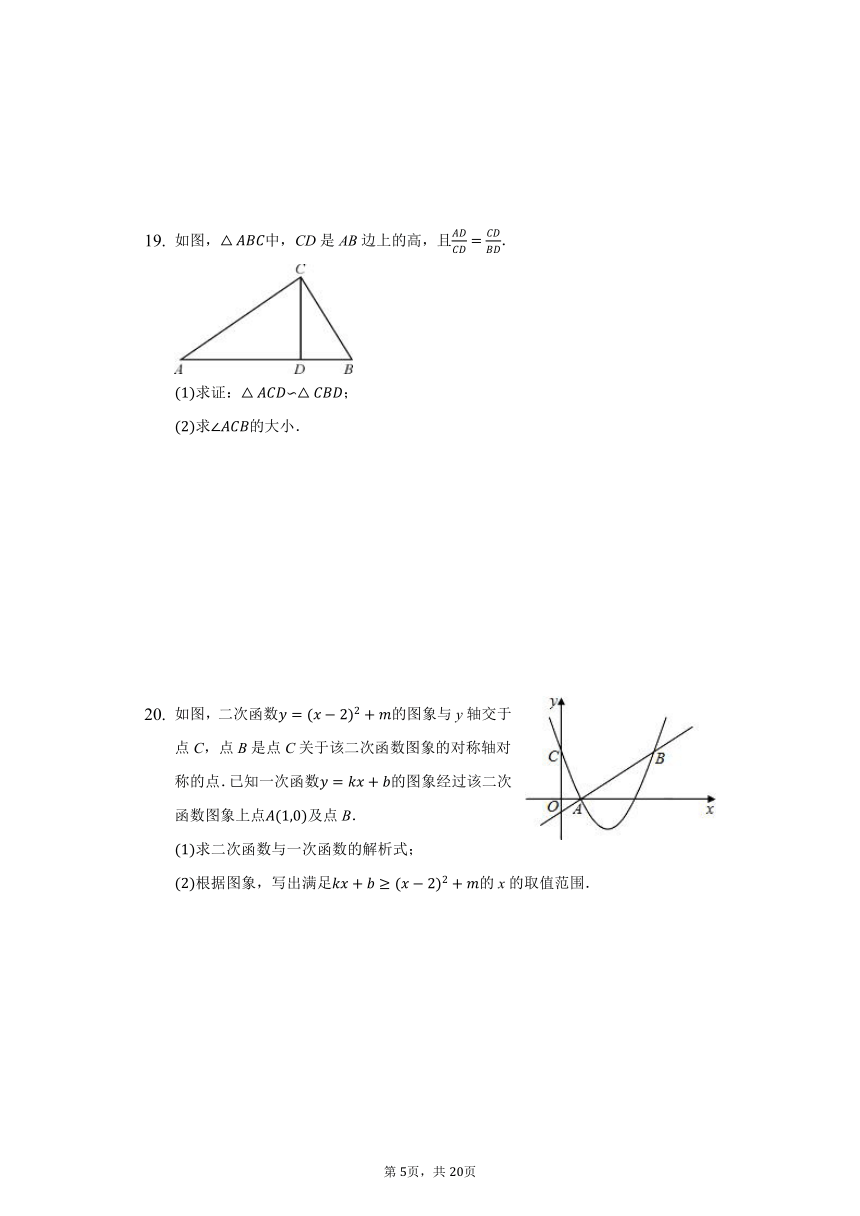
如图,已知一次函数的图象与反比例函数的图象相交于点和点,与x轴交于点C,
求一次函数与反比例函数的解析式;
求的面积.
杂技团进行杂技表演,演员从跷跷板一端A处弹跳到人梯顶端B处,其身体看成一点的路线是抛物线的一部分.
求演员弹跳离地面的最大高度;
已知人梯高米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演能否成功?请说明理由.
如图,中,CD是AB边上的高,且.
求证:∽;
求的大小.
如图,二次函数的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数的图象经过该二次函数图象上点及点B.
求二次函数与一次函数的解析式;
根据图象,写出满足的x的取值范围.
已知:,M为BE中点,求AE:EC的值.
工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到,然后停止煅烧进行锻造操作第时,材料温度降为,煅烧时,温度与时间成一次函数关系锻造时,温度与时间成反比例关系,如图,已知该材料初始温度是.
分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围
根据工艺要求,当材料温度低于时,必须停止操作,那么锻造的操作时间有多长
为了改善小区环境,某小区决定要在一块一边靠墙墙长的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住如图,若设绿化带的AB边长为,绿化带的面积为。?
求y与x之间的函数关系式,并直接写出自变量x的取值范围;
当x为何值时,满足条件的绿化带的面积最大?
答案和解析
1.【答案】D
【解析】解:原函数解析式可化为:,
函数图象的顶点坐标是.
故选:D.
先把二次函数化为顶点式的形式,再得出其顶点坐标即可.
本题考查的是二次函数的性质,根据题意把二次函数的解析式化为顶点式的形式是解答此题的关键.
2.【答案】A
【解析】
【分析】
此题主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.根据平移规律,可得答案.
【解答】
解:先向右平移2个单位,再向上平移1个单位,
得到的新抛物线的表达式为,
故选A.
3.【答案】B
【解析】解:A、,故本选项错误;
B、,故选项正确.
C、,,故本选项错误;
D、,故选项错误.
故选B.
如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
4.【答案】A
【解析】解:由x:y::4:6,得
,.
.
故选:A.
根据比例的性质,可用x表示y,用x表示z,根据分式的性质,可得答案.
本题考查了比例的性质,利用比例的性质得出,是解题关键.
5.【答案】A
【解析】
【试题解析】
【分析】
本题考查了黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值叫做黄金比.熟记黄金分割的公式:较短的线段原线段的,较长的线段原线段的,是解题的关键.
【解答】
解:由于P为线段的黄金分割点,且AP是较长线段;
则.
B选项中只是个近似值,相比A而言,A是准确答案.
故选A.
6.【答案】B
【解析】解:时,,
反比例函数图象在第一,三象限,
,
解得:.
故选:B.
首先根据当时,有则判断函数图象所在象限,再根据所在象限判断的取值范围.
本题主要考查反比例函数的性质,关键是根据题意判断出图象所在象限.
7.【答案】D
【解析】解:如图,抛物线开口方向向上,则故正确;
对称轴方程,即,错误;
抛物线经过原点,故正确;
当时,,即故正确.
综上所述,正确的说法是.
故选D.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
本题考查了二次函数图象与系数的关系.二次函数系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.
8.【答案】D
【解析】解:由函数图象可得,
,故正确,
二次函数的图象过点,对称轴为直线,
当时,,故正确,
,得,故正确,
函数图象开口向下,对称轴为直线,
当时,y随x的增大而增大,
若点、为函数图象上的两点,则,故正确,
故选:D.
根据函数图象和题意,可以判断各个小题中的结论是否正确,从而可以解答本题.
本题考查二次函数图象与系数的关系、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
9.【答案】B
【解析】
【分析】
本题考查了反比例函数图象上点的坐标特征:反比例函数为常数,的图象是双曲线,图象上的点的横纵坐标的积是定值k,即设A点坐标为,根据等腰直角三角形的性质得,,,,则,变形为,利用平方差公式得到,得到,根据反比例函数图象上点的坐标特征易得.
【解答】
解:设A点坐标为,
和都是等腰直角三角形,
,,,,
,
,即,
,
,
.
故选B.
10.【答案】D
【解析】
【分析】
根据二次函数的图象与系数的关系即可求出答案.
本题考查二次函数的综合问题,解题的关键是正确理解二次函数的图象与系数之间的关系,本题属于中等题型.
【解答】
解:由图象开口可知:,由对称轴可知:,,
由抛物线与y轴的交点可知:,,故A正确;
B.由图象可知:,,,,故B正确;
C.由图象可知:顶点的纵坐标大于2,,,,
,故C正确;
D.对称轴,,,故D错误;
故选D.
11.【答案】
【解析】解:抛物线的顶点在x轴上,
,
解得,,
故答案为:.
根据题意,可知抛物线顶点的纵坐标等于0,从而可以求得c的值.
本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
12.【答案】
【解析】
【分析】
本题考查了反比例函数系数k的几何意义,明确是解题的关键.
设点,又点A在函数上,则,即,根据已知条件得到三角形ABC的面积,进而可得结论.?
【解答】
解:设点,又点A在函数上,则,即,
轴,
,
,,
.
故答案为.
13.【答案】
【解析】
【分析】
?本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中为定值是解答此题的关键.设B、D两点的坐标分别为、,再根据点B与点D在反比例函数的图象上求出xy的值,进而可得出C的坐标.
【解答】
解:四边形ABCD是矩形,顶点A的坐标为,
设B、D两点的坐标分别为、,
点B与点D在反比例函数的图象上,
,,
点C的坐标为.
故答案为.
14.【答案】
【解析】
【分析】
本题考查了二次项函数与系数的关系,关键是掌握二次函数的性质:对于二次函数,二次项系数a决定抛物线的开口方向和大小:当时,抛物线向上开口;当时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时即,对称轴在y轴左;当a与b异号时即,对称轴在y轴右.简称:左同右异;常数项c决定抛物线与y轴交点:抛物线与y轴交于;抛物线与x轴交点个数由决定:时,抛物线与x轴有2个交点;时,抛物线与x轴有1个交点;时,抛物线与x轴没有交点.
根据抛物线对称轴方程对进行判断;根据自变量为1时对应的函数值为负数可对进行判断;根据抛物线的对称性,由抛物线与x轴的一个交点为得到抛物线与x轴的另一个交点为,则可对进行判断;由抛物线开口方向得到,由对称轴位置可得,由抛物线与y轴的交点位置可得,于是可对进行判断.
【解答】
解:抛物线的对称轴为直线,
,所以正确;
时,,
,
即,所以错误;
抛物线与x轴的一个交点为
而抛物线的对称轴为直线,
抛物线与x轴的另一个交点为,所以错误;
抛物线开口向上,
,
,
抛物线与y轴的交点在x轴下方,
,
,所以正确.
故答案为.
15.【答案】解:过C作,交GH于N,交EF于M,交AB于Q,如图,
,
四边形AQCD为平行四边形,
,
同理可得,
,
,
:EG::HF::4:5,
,
:::,NH:::,
,,
,.
【解析】【试题解析】
本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边或两边的延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
过C作,交GH于N,交EF于M,交AB于Q,则可判断四边形AQCD为平行四边形,所以,同理可得,则,再利用平行线分线段成比例定理得到DE:EG::HF::4:5,然后根据平行于三角形的一边,并且和其他两边或两边的延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例得到MF:::,NH:::,则可计算出MF和NH,从而得到GH和EF的长
16.【答案】解:设,
则,,,
.
【解析】首先设,即可得,,,然后将其代入,化简即可求得的值.
此题考查了比例的性质.此题比较简单,注意设是解此题的关键.
17.【答案】解:在反比例函数的图象上,
,
又在反比例函数的图象上,
,
,
,
又是一次函数的上的点,
解得,,,
一次函数的解析式为,反比例函数的解析式;
由直线可知,
所以的面积.
【解析】本题考查了反比例函数和一次函数的交点问题,以及用待定系数法求反比例函数和一次函数的解析式,是基础知识要熟练掌握.
由B点的坐标根据待定系数法即可求得在反比例函数的解析式,代入即可求得m,再由待定系数法求出一次函数解析式;
由直线解析式求得C点的坐标,从而求出的面积.
18.【答案】解:将二次函数化成,
当时,y有最大值,,
因此,演员弹跳离地面的最大高度是米.
能成功表演.理由是:
当时,.
即点在抛物线上,
因此,能表演成功.
【解析】本题考查了二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
将二次函数化简为,即可解出的值.
当时代入二次函数可得点B的坐标在抛物线上.
19.【答案】证明:是边AB上的高,
,
.
∽;
解:∽,
,
在中,,
,
,
即.
【解析】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形的判定定理与性质定理.
由两边对应成比例且夹角相等的两个三角形相似,即可证明∽;
由知∽,然后根据相似三角形的对应角相等可得:,然后由,可得:,即.
20.【答案】解:将点代入得,解得,
所以二次函数解析式为;
当时,,
所以C点坐标为,
由于C和B关于对称轴对称,而抛物线的对称轴为直线,
所以B点坐标为,
将、代入得,解得,
所以一次函数解析式为;
当时,.
【解析】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了待定系数法求出一次函数解析式.
先将点代入求出m的值,根据点的对称性确定B点坐标,然后根据待定系数法求出一次函数解析式;
根据图象和A、B的交点坐标可直接求出的x的取值范围.
21.【答案】解:过点M作交AC于点F,
是BE的中点,
,
,
∽,
,
,
,
,
,
,
:::2.
【解析】本题主要考查平行线分线段成比例,相似三角形的判定与性质,过点M作交AC于点F,易证∽,根据相似三角形的对应边成比例进而可得到,再根据平行线分线段成比例进而得到,即可得到,进而得到答案.
22.【答案】解:设锻造时y与x的函数关系式为,
则,,则.
当时,,解得.
锻造时y与x的函数关系式为,
点B的坐标为.
设煅烧时y与x的函数关系式为,
则解得
煅烧时y与x的函数关系式为.
当时,,,
锻造的操作时间为.
【解析】
【分析】本题考查了一次函数,反比例函数的应用根据题意建立函数模型,求出函数解析式,利用函数的思想解决问题是解题的关键.
结合函数图象分当和两种情况分别设函数解析式,再用待定系数法求解析式即可求解;
由题意可知当函数值,代入反比例函数解析式即可求解.
23.【答案】解:由题意得:
,
,?
自变量x的取值范围是;
,
,
,
当时,y有最大值200平方米,
即当时,满足条件的绿化带面积最大.
【解析】本题考查的是二次函数的实际应用.求二次函数的最大小值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.
依题意易求得y与x的函数关系式以及x的取值范围;?
把的函数关系式用配方法化简求得y的最大值即可.
第2页,共2页
第1页,共1页
题号
一
二
三
四
总分
得分
一、选择题(本大题共10小题,共40.0分)
函数图象顶点坐标是
A.
B.
C.
D.
若将抛物线先向右平移2个单位,再向上平移1个单位,得到的新抛物线的表达式为???
A.
B.
C.
D.
下列四组线段中,能构成比例线段的一组是
A.
1cm,3cm,3cm,6cm
B.
2cm,3cm,4cm,6cm
C.
4cm,5m,6cm,
D.
1cm,,3cm,
已知x:y::4:6,则的值为
A.
B.
1
C.
D.
已知点P是线段AB的一个黄金分割点,且,,则PA的长是
A.
B.
C.
D.
在反比例函数图象上有两点,B?,,,则m的取值范围是
A.
B.
C.
D.
如图为二次函数的图象,下列各式中:,,,,正确的只有
A.
B.
C.
D.
如图是二次函数图象的一部分,图象过点,对称轴为直线,给出四个结论:
;????;
若点、为函数图象上的两点,则;
其中正确结论的个数是
A.
1
B.
2
C.
3
D.
4
如图,和都是等腰直角三角形,,且点A在反比例函数的图象上,若,则k的值为
A.
10
B.
5
C.
20
D.
抛物线图象如图所示,下列结论错误的是
A.
B.
C.
D.
二、填空题(本大题共4小题,共20.0分)
若抛物线的顶点在x轴上,则c的取值是______.
如图,在平面直角坐标系中,点A是函数图象上的点,过点A作y轴的垂线交y轴于点B,点C在x轴上,则的面积为______
.
如图,矩形ABCD的边AB与y轴平行,顶点A的坐标为,点B与点D在反比例函数的图象上,则点C的坐标为___________.
二次函数的图象如图所示,下列结论:;;抛物线与x轴的另一个交点为;其中正确的结论是______填写序号
三、计算题(本大题共1小题,共8.0分)
如图,,,,DE:EG::4:求EF和GH的长.
四、解答题(本大题共8小题,共82.0分)
已知,求的值.
如图,已知一次函数的图象与反比例函数的图象相交于点和点,与x轴交于点C,
求一次函数与反比例函数的解析式;
求的面积.
杂技团进行杂技表演,演员从跷跷板一端A处弹跳到人梯顶端B处,其身体看成一点的路线是抛物线的一部分.
求演员弹跳离地面的最大高度;
已知人梯高米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演能否成功?请说明理由.
如图,中,CD是AB边上的高,且.
求证:∽;
求的大小.
如图,二次函数的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数的图象经过该二次函数图象上点及点B.
求二次函数与一次函数的解析式;
根据图象,写出满足的x的取值范围.
已知:,M为BE中点,求AE:EC的值.
工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料煅烧到,然后停止煅烧进行锻造操作第时,材料温度降为,煅烧时,温度与时间成一次函数关系锻造时,温度与时间成反比例关系,如图,已知该材料初始温度是.
分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围
根据工艺要求,当材料温度低于时,必须停止操作,那么锻造的操作时间有多长
为了改善小区环境,某小区决定要在一块一边靠墙墙长的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住如图,若设绿化带的AB边长为,绿化带的面积为。?
求y与x之间的函数关系式,并直接写出自变量x的取值范围;
当x为何值时,满足条件的绿化带的面积最大?
答案和解析
1.【答案】D
【解析】解:原函数解析式可化为:,
函数图象的顶点坐标是.
故选:D.
先把二次函数化为顶点式的形式,再得出其顶点坐标即可.
本题考查的是二次函数的性质,根据题意把二次函数的解析式化为顶点式的形式是解答此题的关键.
2.【答案】A
【解析】
【分析】
此题主要考查了函数图象的平移,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.根据平移规律,可得答案.
【解答】
解:先向右平移2个单位,再向上平移1个单位,
得到的新抛物线的表达式为,
故选A.
3.【答案】B
【解析】解:A、,故本选项错误;
B、,故选项正确.
C、,,故本选项错误;
D、,故选项错误.
故选B.
如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.
此题考查了比例线段,理解成比例线段的概念,注意在线段两两相乘的时候,要让最小的和最大的相乘,另外两条相乘,看它们的积是否相等进行判断.
4.【答案】A
【解析】解:由x:y::4:6,得
,.
.
故选:A.
根据比例的性质,可用x表示y,用x表示z,根据分式的性质,可得答案.
本题考查了比例的性质,利用比例的性质得出,是解题关键.
5.【答案】A
【解析】
【试题解析】
【分析】
本题考查了黄金分割的概念:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值叫做黄金比.熟记黄金分割的公式:较短的线段原线段的,较长的线段原线段的,是解题的关键.
【解答】
解:由于P为线段的黄金分割点,且AP是较长线段;
则.
B选项中只是个近似值,相比A而言,A是准确答案.
故选A.
6.【答案】B
【解析】解:时,,
反比例函数图象在第一,三象限,
,
解得:.
故选:B.
首先根据当时,有则判断函数图象所在象限,再根据所在象限判断的取值范围.
本题主要考查反比例函数的性质,关键是根据题意判断出图象所在象限.
7.【答案】D
【解析】解:如图,抛物线开口方向向上,则故正确;
对称轴方程,即,错误;
抛物线经过原点,故正确;
当时,,即故正确.
综上所述,正确的说法是.
故选D.
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
本题考查了二次函数图象与系数的关系.二次函数系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.
8.【答案】D
【解析】解:由函数图象可得,
,故正确,
二次函数的图象过点,对称轴为直线,
当时,,故正确,
,得,故正确,
函数图象开口向下,对称轴为直线,
当时,y随x的增大而增大,
若点、为函数图象上的两点,则,故正确,
故选:D.
根据函数图象和题意,可以判断各个小题中的结论是否正确,从而可以解答本题.
本题考查二次函数图象与系数的关系、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
9.【答案】B
【解析】
【分析】
本题考查了反比例函数图象上点的坐标特征:反比例函数为常数,的图象是双曲线,图象上的点的横纵坐标的积是定值k,即设A点坐标为,根据等腰直角三角形的性质得,,,,则,变形为,利用平方差公式得到,得到,根据反比例函数图象上点的坐标特征易得.
【解答】
解:设A点坐标为,
和都是等腰直角三角形,
,,,,
,
,即,
,
,
.
故选B.
10.【答案】D
【解析】
【分析】
根据二次函数的图象与系数的关系即可求出答案.
本题考查二次函数的综合问题,解题的关键是正确理解二次函数的图象与系数之间的关系,本题属于中等题型.
【解答】
解:由图象开口可知:,由对称轴可知:,,
由抛物线与y轴的交点可知:,,故A正确;
B.由图象可知:,,,,故B正确;
C.由图象可知:顶点的纵坐标大于2,,,,
,故C正确;
D.对称轴,,,故D错误;
故选D.
11.【答案】
【解析】解:抛物线的顶点在x轴上,
,
解得,,
故答案为:.
根据题意,可知抛物线顶点的纵坐标等于0,从而可以求得c的值.
本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.
12.【答案】
【解析】
【分析】
本题考查了反比例函数系数k的几何意义,明确是解题的关键.
设点,又点A在函数上,则,即,根据已知条件得到三角形ABC的面积,进而可得结论.?
【解答】
解:设点,又点A在函数上,则,即,
轴,
,
,,
.
故答案为.
13.【答案】
【解析】
【分析】
?本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数中为定值是解答此题的关键.设B、D两点的坐标分别为、,再根据点B与点D在反比例函数的图象上求出xy的值,进而可得出C的坐标.
【解答】
解:四边形ABCD是矩形,顶点A的坐标为,
设B、D两点的坐标分别为、,
点B与点D在反比例函数的图象上,
,,
点C的坐标为.
故答案为.
14.【答案】
【解析】
【分析】
本题考查了二次项函数与系数的关系,关键是掌握二次函数的性质:对于二次函数,二次项系数a决定抛物线的开口方向和大小:当时,抛物线向上开口;当时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时即,对称轴在y轴左;当a与b异号时即,对称轴在y轴右.简称:左同右异;常数项c决定抛物线与y轴交点:抛物线与y轴交于;抛物线与x轴交点个数由决定:时,抛物线与x轴有2个交点;时,抛物线与x轴有1个交点;时,抛物线与x轴没有交点.
根据抛物线对称轴方程对进行判断;根据自变量为1时对应的函数值为负数可对进行判断;根据抛物线的对称性,由抛物线与x轴的一个交点为得到抛物线与x轴的另一个交点为,则可对进行判断;由抛物线开口方向得到,由对称轴位置可得,由抛物线与y轴的交点位置可得,于是可对进行判断.
【解答】
解:抛物线的对称轴为直线,
,所以正确;
时,,
,
即,所以错误;
抛物线与x轴的一个交点为
而抛物线的对称轴为直线,
抛物线与x轴的另一个交点为,所以错误;
抛物线开口向上,
,
,
抛物线与y轴的交点在x轴下方,
,
,所以正确.
故答案为.
15.【答案】解:过C作,交GH于N,交EF于M,交AB于Q,如图,
,
四边形AQCD为平行四边形,
,
同理可得,
,
,
:EG::HF::4:5,
,
:::,NH:::,
,,
,.
【解析】【试题解析】
本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.平行于三角形的一边,并且和其他两边或两边的延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例.
过C作,交GH于N,交EF于M,交AB于Q,则可判断四边形AQCD为平行四边形,所以,同理可得,则,再利用平行线分线段成比例定理得到DE:EG::HF::4:5,然后根据平行于三角形的一边,并且和其他两边或两边的延长线相交的直线,所截得的三角形的三边与原三角形的三边对应成比例得到MF:::,NH:::,则可计算出MF和NH,从而得到GH和EF的长
16.【答案】解:设,
则,,,
.
【解析】首先设,即可得,,,然后将其代入,化简即可求得的值.
此题考查了比例的性质.此题比较简单,注意设是解此题的关键.
17.【答案】解:在反比例函数的图象上,
,
又在反比例函数的图象上,
,
,
,
又是一次函数的上的点,
解得,,,
一次函数的解析式为,反比例函数的解析式;
由直线可知,
所以的面积.
【解析】本题考查了反比例函数和一次函数的交点问题,以及用待定系数法求反比例函数和一次函数的解析式,是基础知识要熟练掌握.
由B点的坐标根据待定系数法即可求得在反比例函数的解析式,代入即可求得m,再由待定系数法求出一次函数解析式;
由直线解析式求得C点的坐标,从而求出的面积.
18.【答案】解:将二次函数化成,
当时,y有最大值,,
因此,演员弹跳离地面的最大高度是米.
能成功表演.理由是:
当时,.
即点在抛物线上,
因此,能表演成功.
【解析】本题考查了二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
将二次函数化简为,即可解出的值.
当时代入二次函数可得点B的坐标在抛物线上.
19.【答案】证明:是边AB上的高,
,
.
∽;
解:∽,
,
在中,,
,
,
即.
【解析】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形的判定定理与性质定理.
由两边对应成比例且夹角相等的两个三角形相似,即可证明∽;
由知∽,然后根据相似三角形的对应角相等可得:,然后由,可得:,即.
20.【答案】解:将点代入得,解得,
所以二次函数解析式为;
当时,,
所以C点坐标为,
由于C和B关于对称轴对称,而抛物线的对称轴为直线,
所以B点坐标为,
将、代入得,解得,
所以一次函数解析式为;
当时,.
【解析】本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.也考查了待定系数法求出一次函数解析式.
先将点代入求出m的值,根据点的对称性确定B点坐标,然后根据待定系数法求出一次函数解析式;
根据图象和A、B的交点坐标可直接求出的x的取值范围.
21.【答案】解:过点M作交AC于点F,
是BE的中点,
,
,
∽,
,
,
,
,
,
,
:::2.
【解析】本题主要考查平行线分线段成比例,相似三角形的判定与性质,过点M作交AC于点F,易证∽,根据相似三角形的对应边成比例进而可得到,再根据平行线分线段成比例进而得到,即可得到,进而得到答案.
22.【答案】解:设锻造时y与x的函数关系式为,
则,,则.
当时,,解得.
锻造时y与x的函数关系式为,
点B的坐标为.
设煅烧时y与x的函数关系式为,
则解得
煅烧时y与x的函数关系式为.
当时,,,
锻造的操作时间为.
【解析】
【分析】本题考查了一次函数,反比例函数的应用根据题意建立函数模型,求出函数解析式,利用函数的思想解决问题是解题的关键.
结合函数图象分当和两种情况分别设函数解析式,再用待定系数法求解析式即可求解;
由题意可知当函数值,代入反比例函数解析式即可求解.
23.【答案】解:由题意得:
,
,?
自变量x的取值范围是;
,
,
,
当时,y有最大值200平方米,
即当时,满足条件的绿化带面积最大.
【解析】本题考查的是二次函数的实际应用.求二次函数的最大小值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.
依题意易求得y与x的函数关系式以及x的取值范围;?
把的函数关系式用配方法化简求得y的最大值即可.
第2页,共2页
第1页,共1页
同课章节目录
