七年级数学7.3.2多边形的内角和
文档属性
| 名称 | 七年级数学7.3.2多边形的内角和 |

|
|
| 格式 | rar | ||
| 文件大小 | 248.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-23 20:04:14 | ||
图片预览





文档简介
(共19张PPT)
主讲人:09数一 杨思韵
1 . 什么叫做多边形?
由 多 条不在同一直线上的线段首尾顺次连结组成的平面图形,称为 多边形。
2 . 什么叫做对角线?
连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
3 . 什么叫做正多边形?
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。
温
故
知
新
你能想到什么方法得出下面的四边形的内角和?
D
C
B
A
三角形的内角和等于180°。
A
B
C
以前我们学过
多边形的内角和与三角形的内角和有没有联系?
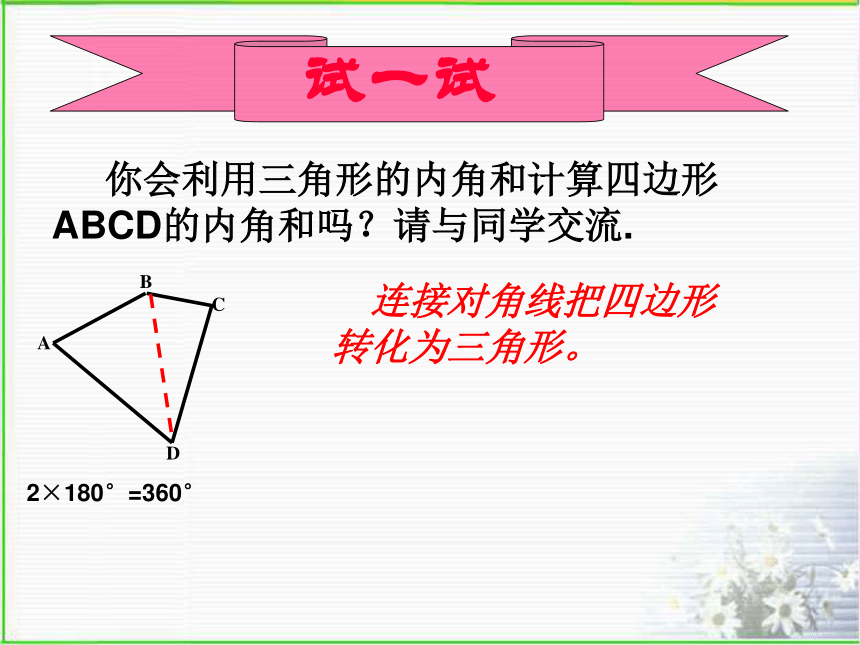
试一试
你会利用三角形的内角和计算四边形ABCD的内角和吗?请与同学交流.
D
C
B
A
2×180°=360°
连接对角线把四边形转化为三角形。
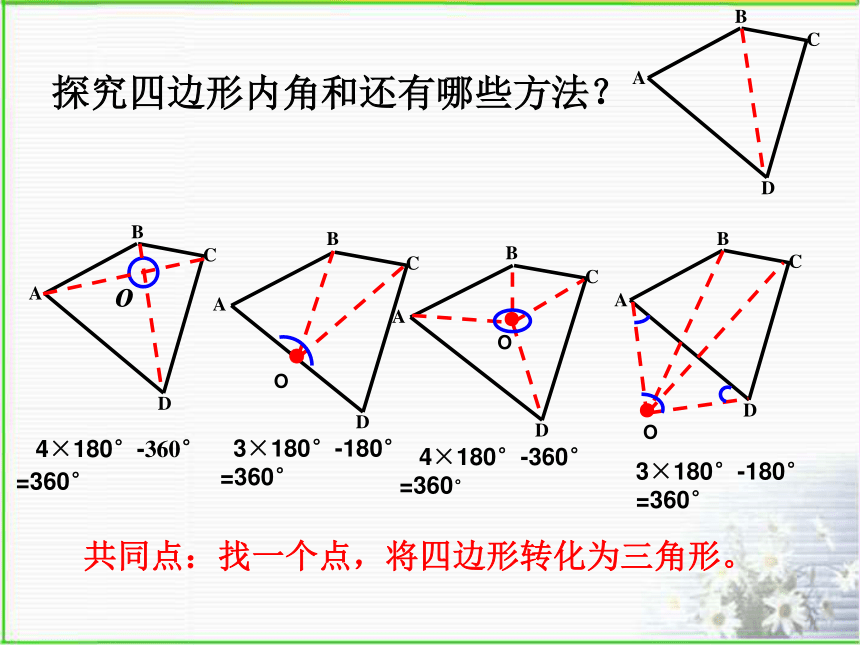
探究四边形内角和还有哪些方法?
D
C
B
A
D
C
B
A
O
D
C
B
A
O
D
C
B
A
O
●
●
●
4×180°-360° =360°
3×180°-180°
=360°
4×180°-360°
=360°
3×180°-180°
=360°
共同点:找一个点,将四边形转化为三角形。
D
C
B
A
o
多边形 边数 分成三角形的个数 图形
计算规律
内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
5
6
7
n
1
n-2
3
4
5
180°
540°
720°
900°
(n-2) ·180°
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
4
2
360°
2 ×180°
想一想
尝试完成下表,你有什么发现?
1 ×180°
结论:n边形内角和公式为:_________。
B
A
C
D
G
F
E
(n-2)·180°
①n代表什么?
② n-2表示什么含义?
③为什么要乘以180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
D
C
B
A
例1 如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
解:如图所示,四边形ABCD中,
∠A + ∠C = 180°.
因为
∠A + ∠ B +∠C + ∠D = (4-2) ×180°= 360°.
所以 ∠ B + ∠D = 360°- (∠A + ∠C )
= 360°- 180°= 180°
(1)十二边形的内角和是多少?
解:(12-2)×180°
=10 ×180°
=1800 °
答:十二边形的内角和为1800 °
练一练
(2)一个多边形的内角和为2700°,求它的边数。
解 :设这是一个n边形,根据题意得:
(n-2)·180 °=2700 °
解得: n=17
答:它的边数为17.
6
E
B
C
D
1
2
3
4
5
A
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
5边形外角和
结论:五边形的外角和等于360°
-(5-2) × 180°
=360 °
=5个平角
-5边形内角和
=5×180°
议一议
猜一猜,七边形、八边形以及n边形的外角和各是多少?你的结论是什么?
n边形外角和
结论:
多边形的外角和等于360°
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
=n×180 °
A
1
E
B
C
D
2
3
4
5
F
n
试一试
议一议
(1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?
在图中标出它们.
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)你能说明上述结论的正确性吗?
♀
清晨 ,小明沿一个五边形广场周围的小路按逆时针方向跑步。
达标检测
(1)若一个多边形的边数增加1,则这个多边形的内角增加_____度。
(2)九边形的内角和是__________
(3)已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为 ;
180
1260°
6
今天的收获
1、n边形的内角和等于:
(n-2)×180°
2、利用类比归纳、转化的学习方法, 可以把多边形问题转化为三角形问题来解决;
3、方程的数学思想在几何中有重要的作用。
A组:课本P62:5、6、7
作业:
D
C
B
E
A
F
B组:
已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
C组:
如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
谢谢大家的观看!
主讲人:09数一 杨思韵
1 . 什么叫做多边形?
由 多 条不在同一直线上的线段首尾顺次连结组成的平面图形,称为 多边形。
2 . 什么叫做对角线?
连结多边形不相邻的两个顶点的线段叫做多边形的对角线。
3 . 什么叫做正多边形?
如果多边形的各边都相等,各内角也都相等,那么就称它为正多边形。
温
故
知
新
你能想到什么方法得出下面的四边形的内角和?
D
C
B
A
三角形的内角和等于180°。
A
B
C
以前我们学过
多边形的内角和与三角形的内角和有没有联系?
试一试
你会利用三角形的内角和计算四边形ABCD的内角和吗?请与同学交流.
D
C
B
A
2×180°=360°
连接对角线把四边形转化为三角形。
探究四边形内角和还有哪些方法?
D
C
B
A
D
C
B
A
O
D
C
B
A
O
D
C
B
A
O
●
●
●
4×180°-360° =360°
3×180°-180°
=360°
4×180°-360°
=360°
3×180°-180°
=360°
共同点:找一个点,将四边形转化为三角形。
D
C
B
A
o
多边形 边数 分成三角形的个数 图形
计算规律
内角和
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
5
6
7
n
1
n-2
3
4
5
180°
540°
720°
900°
(n-2) ·180°
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
4
2
360°
2 ×180°
想一想
尝试完成下表,你有什么发现?
1 ×180°
结论:n边形内角和公式为:_________。
B
A
C
D
G
F
E
(n-2)·180°
①n代表什么?
② n-2表示什么含义?
③为什么要乘以180°
这就是说,如果四边形的一组对角互补,那么另一组对角也互补。
D
C
B
A
例1 如果一个四边形的一组对角互补,
那么另一组对角有什么关系?
解:如图所示,四边形ABCD中,
∠A + ∠C = 180°.
因为
∠A + ∠ B +∠C + ∠D = (4-2) ×180°= 360°.
所以 ∠ B + ∠D = 360°- (∠A + ∠C )
= 360°- 180°= 180°
(1)十二边形的内角和是多少?
解:(12-2)×180°
=10 ×180°
=1800 °
答:十二边形的内角和为1800 °
练一练
(2)一个多边形的内角和为2700°,求它的边数。
解 :设这是一个n边形,根据题意得:
(n-2)·180 °=2700 °
解得: n=17
答:它的边数为17.
6
E
B
C
D
1
2
3
4
5
A
1.任意一个外角和它相邻的内角有什么关系?
2.五个外角加上它们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系?
5边形外角和
结论:五边形的外角和等于360°
-(5-2) × 180°
=360 °
=5个平角
-5边形内角和
=5×180°
议一议
猜一猜,七边形、八边形以及n边形的外角和各是多少?你的结论是什么?
n边形外角和
结论:
多边形的外角和等于360°
-(n-2) × 180°
=360 °
=n个平角-n边形内角和
=n×180 °
A
1
E
B
C
D
2
3
4
5
F
n
试一试
议一议
(1)小明每从一条小路转到下一条小路时,身体转过的角是哪个角?
在图中标出它们.
(2)他每跑完一圈,身体转过的角度之和是多少?
(3)你能说明上述结论的正确性吗?
♀
清晨 ,小明沿一个五边形广场周围的小路按逆时针方向跑步。
达标检测
(1)若一个多边形的边数增加1,则这个多边形的内角增加_____度。
(2)九边形的内角和是__________
(3)已知一个多边形的边数恰好是从一个顶点所画的对角线的条数的2倍,则此多边形的边数为 ;
180
1260°
6
今天的收获
1、n边形的内角和等于:
(n-2)×180°
2、利用类比归纳、转化的学习方法, 可以把多边形问题转化为三角形问题来解决;
3、方程的数学思想在几何中有重要的作用。
A组:课本P62:5、6、7
作业:
D
C
B
E
A
F
B组:
已知一个多边形除了一个内角外,其余各内角的和是2750°,求这个多边形的边数。
C组:
如图:我国的国旗上的五星是正五角星,正五角星中的五边形ABCDE是正五边形,你能求出五角星中∠F的度数?
谢谢大家的观看!
