六年级数学上册课件-5.4 扇形-人教版(共59张PPT)
文档属性
| 名称 | 六年级数学上册课件-5.4 扇形-人教版(共59张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 15:13:54 | ||
图片预览







文档简介
(共59张PPT)
扇
形
这些物体的形状有什么共同的地方?
扇
形
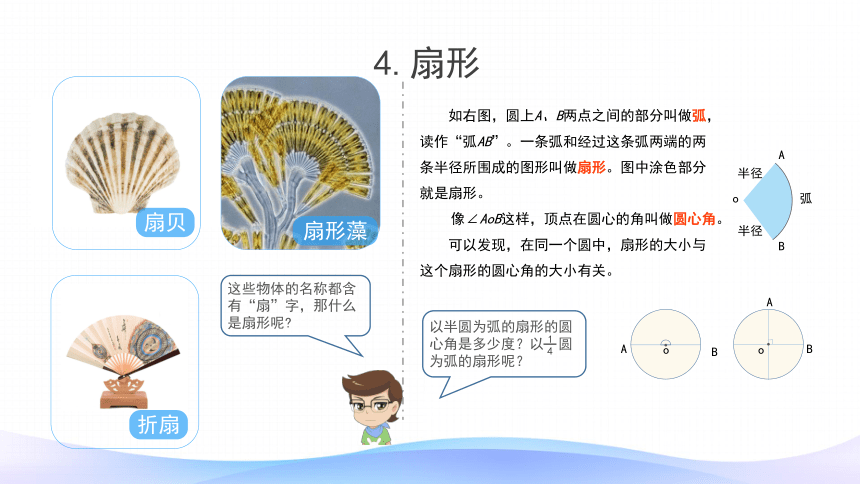
4.扇形
扇贝
扇形藻
折扇
这些物体的名称都含有“扇”字,那什么是扇形呢?
以半圆为弧的扇形的圆心角是多少度?以
圆为弧的扇形呢?
A
o
B
o
A
B
B
A
o
半径
半径
弧
如右图,圆上A、B两点之间的部分叫做弧,读作“弧AB”。一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。图中涂色部分就是扇形。
像∠AoB这样,顶点在圆心的角叫做圆心角。
可以发现,在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
1
4
一条弧和经过这条弧两
端的两条半径所围成的图形
叫做扇形。
什么是扇形?
一条弧和经过这条弧两
端的两条半径所围成的图形
叫做扇形。
一条弧和经过这条弧两
端的两条半径所围成的图形
叫做扇形。
一条弧
两条半径
扇形
圆上AB两点之间的部分叫做弧。
什么是弧?
O
o
A
B
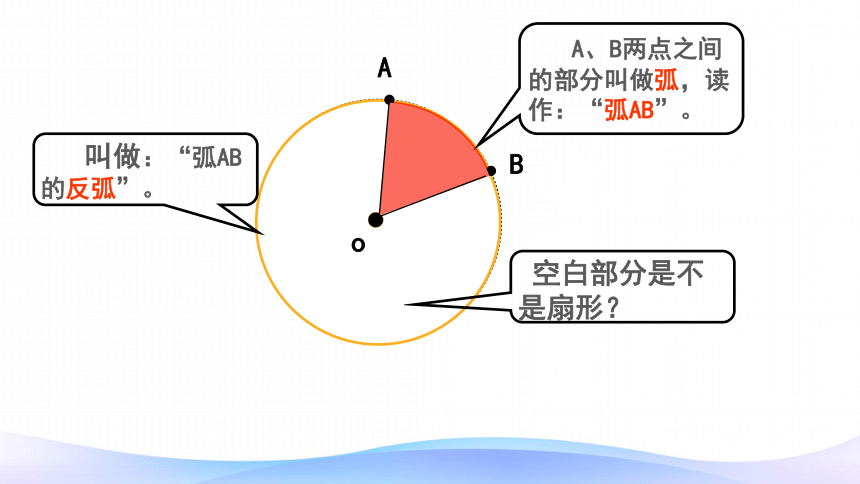
A、B两点之间的部分叫做弧,读作:“弧AB”。
叫做:“弧AB的反弧”。
空白部分是不是扇形?
O
o
A
B
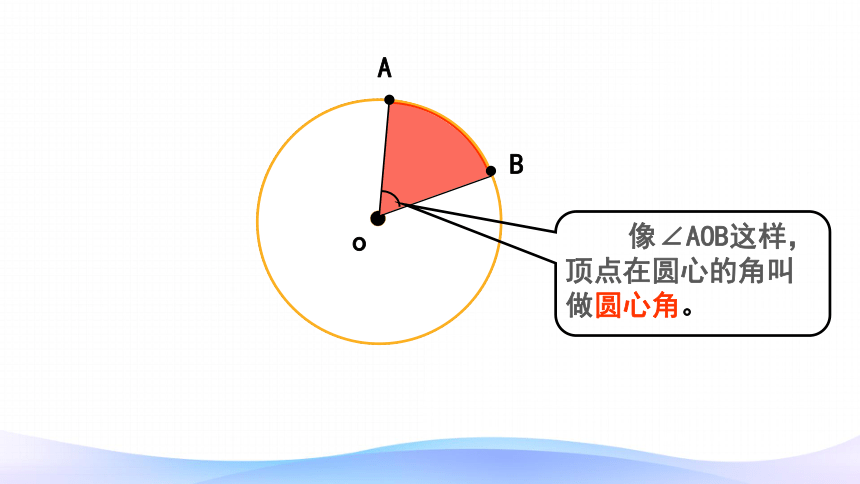
像∠AOB这样,顶点在圆心的角叫做圆心角。
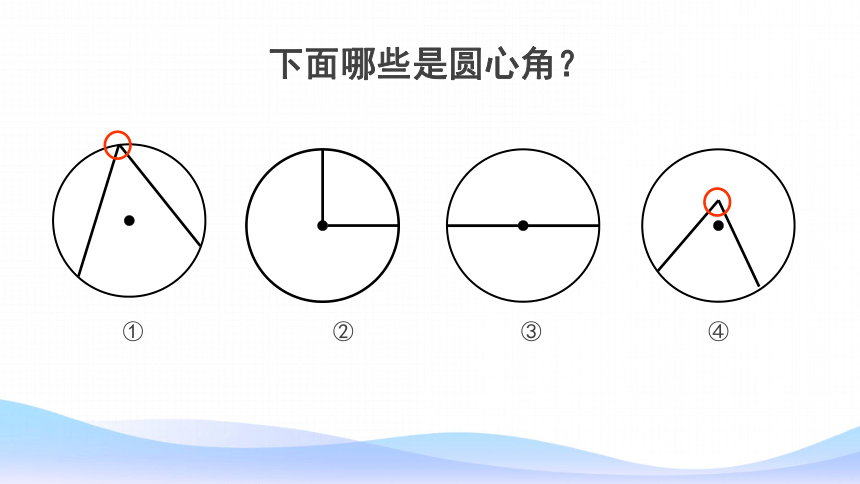
下面哪些是圆心角?
①
②
③
④
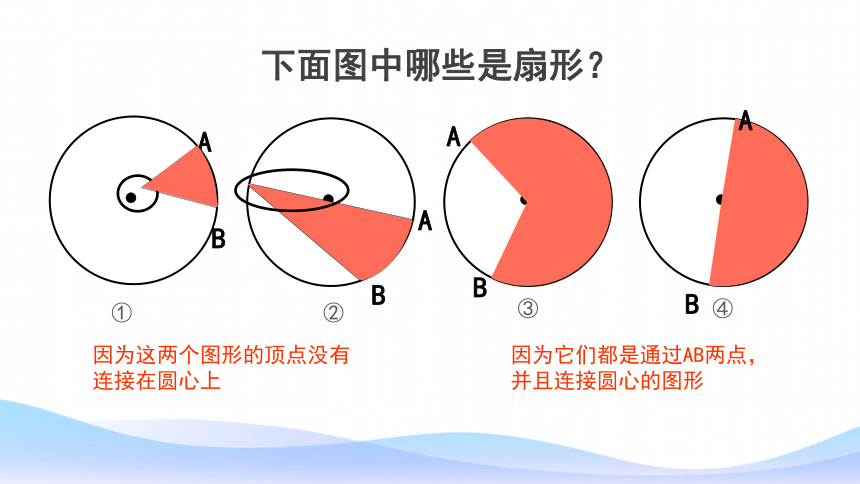
下面图中哪些是扇形?
①
②
③
④
因为它们都是通过AB两点,并且连接圆心的图形
A
B
A
B
A
B
A
B
因为这两个图形的顶点没有连接在圆心上
课堂练习
画一画
先画出一个任意大小的圆,
使扇形的圆心角为60度。
学生作业1
o
5cm
60o
学生作业2
o
3cm
60o
比较两个扇形的大小
学生作业
60o
60o
3cm
5cm
<
学生作业
60o
60o
4cm
2cm
<
半径不同,它们的扇形面积也不同。
60o
60o
比较两个扇形的大小
在大小不同的圆中,圆心角虽然相等,因为半径
不同,所以扇形的大小也不同。半径越大,扇形面积
就越大,扇形的大小和半径有关
。
120o
40o
比较两个扇形的大小
在
中,扇形的大小与这个扇形的
的大小有关,
大的扇形面积大,
小的扇形面积小。
圆心角
同一个圆或等圆
圆心角
圆心角
如何画出两个完全相同的扇形?
先画两条相等的半径,再画相同角度的扇形。
先画等圆,因为半径和圆心角相等,画出的扇形相等。
先画两个相等的圆,之后再画出度数一样的扇形。
60o
60o
扇形的大小与半径的长短和圆心角的大小有关。
比较两个扇形的大小
怎样计算扇形的面积?
以半圆为弧的扇形
以1/4圆为弧的扇形
这两个扇形的圆心角是多少度?
90o
180o
以半圆为弧的扇形
以1/4圆为弧的扇形
90o
扇形的面积所占圆面积的几分之几?
180o
以半圆为弧的扇形
扇形的面积所占圆面积的几分之几?
扇形面积=圆面积×
2
1
180o
扇形面积=圆面积×
360o
180o
以1/4圆为弧的扇形
90o
扇形面积=圆面积×
4
1
扇形面积=圆面积×
360o
90o
扇形的面积所占圆面积的几分之几?
以半圆为弧的扇形
以1/4圆为弧的扇形
90o
180o
扇形的面积所占圆面积的几分之几?
二分之一
四分之一
360o
360o
扇形面积=圆面积×
360o
180o
扇形面积=圆面积×
360o
90o
圆心角
圆心角
扇形的面积和圆心角的大小有关
如果圆心角为no
扇形的面积=圆面积×
360o
no
扇形的面积和圆心角的大小有关
问题:如果圆心角是60度的话,这个扇形的面积是它所占圆面积的几分之几?
回答:六分之一
问题:如果圆心角是20度的话,那这个扇形的面积是它所占圆面积的几分之几呢?
回答:十八分之一
360o
20o
=
18
1
问题:如果圆心角是40度的扇形,它所占圆面积的几分之几呢?
回答:九分之一
1.因为扇形是它所在圆的一部分,那么圆的
一部分一定是扇形。
(
)
×
判断
因为:如果没有连接到圆心或者AB两点的话,就不是扇形。
2.圆的面积比扇形的面积大。
(
)
×
判断
3.顶点在圆上的角是圆心角。
(
)
×
判断
因为:圆心角的顶点在圆心上。
4.半圆也是一个扇形。
(
)
√
判断
因为:半圆是一个圆心角180度的扇形。
1.扇形圆心角的度数是(
)
A
大于0o
B
大于360o
C
大于0o小于360o
D
任意度
选择
c
扇形只是圆的一部分
2.扇形的大小(
)
A
只与圆心角的大小有关
B
只与半径的长短有关
C
与圆心角的大小、半径的长短都有关
选择
c
生活中的扇形物件
耳环
盘子
玻璃
灯
120o
60o
求出扇形的面积
r=3cm
r=3cm
学生作业
s
=32×3.14×
=32×3.14×
=4.71(cm2)
360o
60o
6
1
60o
r=3cm
学生作业
s
=3×3×3.14×
=3×3×3.14×
=9.42(cm2)
360o
120o
3
1
120o
r=3cm
求出扇形的面积
s
=πr2×
=3.14×32×
=4.71(cm2)
360o
no
360o
60o
s
=πr2×
=3.14×32×
=9.42(cm2)
360o
no
360o
120o
求下面扇环的面积
1.先算大扇形的面积
2.再算出小扇形的面积
3.大扇形面积减去小扇
形面积
4.得出扇环面积
求下面扇环的面积
120o
9cm
3cm
学生作业1
9×9×3.14×
-3×3×
3
1
3
1
360o
120o
9cm
?
6×6
3cm
求下面扇环的面积
R=9(cm)
r=9-3=6(cm)
S=πR2×
-πr2
×
=3.14
×81×
-3.14
×36×
=47.1(cm2)
360o
120o
360o
120o
3
1
3
1
根据08年北京奥运会,中国、美国、俄罗斯三个国家获得的金牌数,绘制了这样一幅图,你们从这副图中发现了什么?
中国
美国
俄罗斯
看到了这样一幅图,你有什么想说的?
中国
美国
俄罗斯
1984年,第23届洛杉矶奥运会上,中国射击运动员许海峰为中国获得首枚金牌,是我国参加奥运会历史上首位冠军得主,实现中国奥运史上金牌“零”的突破。
许海峰
你有何感想?
努力学习,发愤图强。
我为我们的祖国感到骄傲。
努力学习,以后也成为祖国的骄傲。
你有哪些收获?
我知道了扇环,我也知道怎么样计算扇环的面积。
我知道什么是扇形,还知道了怎么计算出扇形的面积。
你有哪些收获?
我知道怎么算圆的面积。
我知道了弧是什么。
小结
认识了什么是扇形。
知道怎样计算扇形的面积。
也知道了如何计算扇环的面积。
再见!
扇
形
这些物体的形状有什么共同的地方?
扇
形
4.扇形
扇贝
扇形藻
折扇
这些物体的名称都含有“扇”字,那什么是扇形呢?
以半圆为弧的扇形的圆心角是多少度?以
圆为弧的扇形呢?
A
o
B
o
A
B
B
A
o
半径
半径
弧
如右图,圆上A、B两点之间的部分叫做弧,读作“弧AB”。一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。图中涂色部分就是扇形。
像∠AoB这样,顶点在圆心的角叫做圆心角。
可以发现,在同一个圆中,扇形的大小与这个扇形的圆心角的大小有关。
1
4
一条弧和经过这条弧两
端的两条半径所围成的图形
叫做扇形。
什么是扇形?
一条弧和经过这条弧两
端的两条半径所围成的图形
叫做扇形。
一条弧和经过这条弧两
端的两条半径所围成的图形
叫做扇形。
一条弧
两条半径
扇形
圆上AB两点之间的部分叫做弧。
什么是弧?
O
o
A
B
A、B两点之间的部分叫做弧,读作:“弧AB”。
叫做:“弧AB的反弧”。
空白部分是不是扇形?
O
o
A
B
像∠AOB这样,顶点在圆心的角叫做圆心角。
下面哪些是圆心角?
①
②
③
④
下面图中哪些是扇形?
①
②
③
④
因为它们都是通过AB两点,并且连接圆心的图形
A
B
A
B
A
B
A
B
因为这两个图形的顶点没有连接在圆心上
课堂练习
画一画
先画出一个任意大小的圆,
使扇形的圆心角为60度。
学生作业1
o
5cm
60o
学生作业2
o
3cm
60o
比较两个扇形的大小
学生作业
60o
60o
3cm
5cm
<
学生作业
60o
60o
4cm
2cm
<
半径不同,它们的扇形面积也不同。
60o
60o
比较两个扇形的大小
在大小不同的圆中,圆心角虽然相等,因为半径
不同,所以扇形的大小也不同。半径越大,扇形面积
就越大,扇形的大小和半径有关
。
120o
40o
比较两个扇形的大小
在
中,扇形的大小与这个扇形的
的大小有关,
大的扇形面积大,
小的扇形面积小。
圆心角
同一个圆或等圆
圆心角
圆心角
如何画出两个完全相同的扇形?
先画两条相等的半径,再画相同角度的扇形。
先画等圆,因为半径和圆心角相等,画出的扇形相等。
先画两个相等的圆,之后再画出度数一样的扇形。
60o
60o
扇形的大小与半径的长短和圆心角的大小有关。
比较两个扇形的大小
怎样计算扇形的面积?
以半圆为弧的扇形
以1/4圆为弧的扇形
这两个扇形的圆心角是多少度?
90o
180o
以半圆为弧的扇形
以1/4圆为弧的扇形
90o
扇形的面积所占圆面积的几分之几?
180o
以半圆为弧的扇形
扇形的面积所占圆面积的几分之几?
扇形面积=圆面积×
2
1
180o
扇形面积=圆面积×
360o
180o
以1/4圆为弧的扇形
90o
扇形面积=圆面积×
4
1
扇形面积=圆面积×
360o
90o
扇形的面积所占圆面积的几分之几?
以半圆为弧的扇形
以1/4圆为弧的扇形
90o
180o
扇形的面积所占圆面积的几分之几?
二分之一
四分之一
360o
360o
扇形面积=圆面积×
360o
180o
扇形面积=圆面积×
360o
90o
圆心角
圆心角
扇形的面积和圆心角的大小有关
如果圆心角为no
扇形的面积=圆面积×
360o
no
扇形的面积和圆心角的大小有关
问题:如果圆心角是60度的话,这个扇形的面积是它所占圆面积的几分之几?
回答:六分之一
问题:如果圆心角是20度的话,那这个扇形的面积是它所占圆面积的几分之几呢?
回答:十八分之一
360o
20o
=
18
1
问题:如果圆心角是40度的扇形,它所占圆面积的几分之几呢?
回答:九分之一
1.因为扇形是它所在圆的一部分,那么圆的
一部分一定是扇形。
(
)
×
判断
因为:如果没有连接到圆心或者AB两点的话,就不是扇形。
2.圆的面积比扇形的面积大。
(
)
×
判断
3.顶点在圆上的角是圆心角。
(
)
×
判断
因为:圆心角的顶点在圆心上。
4.半圆也是一个扇形。
(
)
√
判断
因为:半圆是一个圆心角180度的扇形。
1.扇形圆心角的度数是(
)
A
大于0o
B
大于360o
C
大于0o小于360o
D
任意度
选择
c
扇形只是圆的一部分
2.扇形的大小(
)
A
只与圆心角的大小有关
B
只与半径的长短有关
C
与圆心角的大小、半径的长短都有关
选择
c
生活中的扇形物件
耳环
盘子
玻璃
灯
120o
60o
求出扇形的面积
r=3cm
r=3cm
学生作业
s
=32×3.14×
=32×3.14×
=4.71(cm2)
360o
60o
6
1
60o
r=3cm
学生作业
s
=3×3×3.14×
=3×3×3.14×
=9.42(cm2)
360o
120o
3
1
120o
r=3cm
求出扇形的面积
s
=πr2×
=3.14×32×
=4.71(cm2)
360o
no
360o
60o
s
=πr2×
=3.14×32×
=9.42(cm2)
360o
no
360o
120o
求下面扇环的面积
1.先算大扇形的面积
2.再算出小扇形的面积
3.大扇形面积减去小扇
形面积
4.得出扇环面积
求下面扇环的面积
120o
9cm
3cm
学生作业1
9×9×3.14×
-3×3×
3
1
3
1
360o
120o
9cm
?
6×6
3cm
求下面扇环的面积
R=9(cm)
r=9-3=6(cm)
S=πR2×
-πr2
×
=3.14
×81×
-3.14
×36×
=47.1(cm2)
360o
120o
360o
120o
3
1
3
1
根据08年北京奥运会,中国、美国、俄罗斯三个国家获得的金牌数,绘制了这样一幅图,你们从这副图中发现了什么?
中国
美国
俄罗斯
看到了这样一幅图,你有什么想说的?
中国
美国
俄罗斯
1984年,第23届洛杉矶奥运会上,中国射击运动员许海峰为中国获得首枚金牌,是我国参加奥运会历史上首位冠军得主,实现中国奥运史上金牌“零”的突破。
许海峰
你有何感想?
努力学习,发愤图强。
我为我们的祖国感到骄傲。
努力学习,以后也成为祖国的骄傲。
你有哪些收获?
我知道了扇环,我也知道怎么样计算扇环的面积。
我知道什么是扇形,还知道了怎么计算出扇形的面积。
你有哪些收获?
我知道怎么算圆的面积。
我知道了弧是什么。
小结
认识了什么是扇形。
知道怎样计算扇形的面积。
也知道了如何计算扇环的面积。
再见!
