江苏省扬州市2020-2021学年度第一学期高三适应性练习试题高三数学试题 PDF版含答案
文档属性
| 名称 | 江苏省扬州市2020-2021学年度第一学期高三适应性练习试题高三数学试题 PDF版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:45:22 | ||
图片预览




文档简介
2020—2021学年度第一学期高三适应性练习试题
高三数学
2021.1
(全卷满分150分,考试时间:120分钟
项选择題(本大题共8小题,每5分,共40分,在每小题给出的选项中,只有一项符合要求)
1已知集合A={x|(x-2(x
2已知复数z满足(+)=2,则的共轭复数在复平面内对应的点位于()
A第一象限
B第二象限
第三象限
D第四象限
3(2-x)(1+2x)展开式中,含x2项的系数为
B.30
4如图是某品牌手机的商标图案,制作时以曲线段AB为分界线,裁去-部分图形而成
已知该分界线是一段半径为R的圆弧,若圆弧的长度为一,,则A,B两点间的距离为
5已知正ΔABC的边长为2,P是AB边上一点,且BP=2PA
6过抛物线y2=4x焦点F的直线/交抛物线于AB两点(点A在第一象限),若直线l的倾斜角为60°,则
的值为(
7已知数列{n是各项均为正数的等比数列,若a3-a2=5,则a+8a2的最小值为(
x2|的最大值为
多项选择题(本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要
得5分,部分选对的得3分,有选错的得0分)
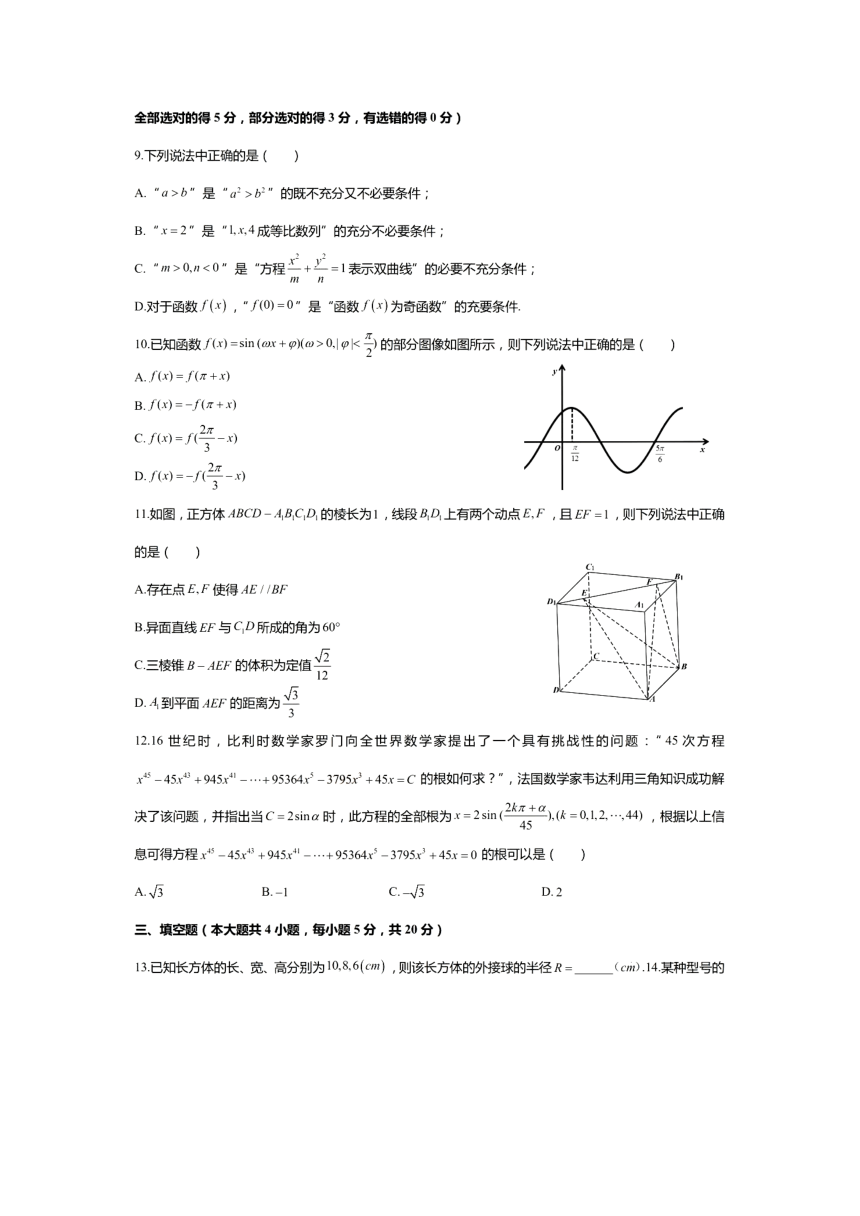
9.下列说法中正确的是(
a>b"是“a2>b2”的既不充分又不必要条件
是"L,x4成等比数列"的充分不必要条件
是“方程
表示双曲线”的必要不充分条件
D对于函数/(x),“f(0)=0“是“函数f(x)为奇函数”的充要条件
10已知函数f(x)-sin(ax+o>0k2)的部分图像如图所示,则下列说法中正确的是()
如图,正方体ABCD-ABCD的棱长为1,线段BD上有两个动点E,F,且EF=1,则下列说法中正确
的是
存在点E,F使得AE∥BF
B.异面直线EF与CD所成的角为6
棱锥B-AEF的体积为定值
D.A到平面AEF的距离为
12.16世纪时,比利时数学家罗门向全世界数学家提出了一个具有挑战性的问题
次方程
95364x-3795x+45x=C的根如何求?
国数学家韦达利用三角知识成功解
决了该问题,并指出当C=2sina时,此方程的全部根为x-2si(
息可得方程x4-45x43+94
95x+4
的根可以是
空题(本大题共4小题,每小题5分,共20分)
3已知长方体的长、宽、高分别为1086(m),则该长方体的外接球的半径R
机器使用总时间X(年)(其中x≥4
)与所需支出的维修总费用(万元)的统计数据如下表:根
据表中数据可得与X之间的线性回归方程为y=0
若该设备维修总费用超过12万元就报废,据此
模型预测该设备最多可使用
年(填整数)
是勾股定理,一个是黄金分割,其中顶角为36°的等腰
三角形被称为“黄金三角形”如图,已知五角星是由5个“黄金三角形”与1个正五
组成
部分的面积为S,正五边形的面积为S
☆
S1
6已知双曲线C
石右顶点为A
交于M,N两点,若OM=2ON(其中O为坐标原点),则双曲线的离心率为
解答題(本大题共6小题,计70分,解答应写出必要的文字说明、证明过程或演算步骤
17、(本小满分10分
在△ABC中,角4,B,C的对边分别为a,,C,△4BC的面积为
1)求B
bc这三个条件中任选一个,补充在上面的问题中
并加以解答.
解答,按第一个解答计
高三数学
2021.1
(全卷满分150分,考试时间:120分钟
项选择題(本大题共8小题,每5分,共40分,在每小题给出的选项中,只有一项符合要求)
1已知集合A={x|(x-2(x
2已知复数z满足(+)=2,则的共轭复数在复平面内对应的点位于()
A第一象限
B第二象限
第三象限
D第四象限
3(2-x)(1+2x)展开式中,含x2项的系数为
B.30
4如图是某品牌手机的商标图案,制作时以曲线段AB为分界线,裁去-部分图形而成
已知该分界线是一段半径为R的圆弧,若圆弧的长度为一,,则A,B两点间的距离为
5已知正ΔABC的边长为2,P是AB边上一点,且BP=2PA
6过抛物线y2=4x焦点F的直线/交抛物线于AB两点(点A在第一象限),若直线l的倾斜角为60°,则
的值为(
7已知数列{n是各项均为正数的等比数列,若a3-a2=5,则a+8a2的最小值为(
x2|的最大值为
多项选择题(本题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要
得5分,部分选对的得3分,有选错的得0分)
9.下列说法中正确的是(
a>b"是“a2>b2”的既不充分又不必要条件
是"L,x4成等比数列"的充分不必要条件
是“方程
表示双曲线”的必要不充分条件
D对于函数/(x),“f(0)=0“是“函数f(x)为奇函数”的充要条件
10已知函数f(x)-sin(ax+o>0k2)的部分图像如图所示,则下列说法中正确的是()
如图,正方体ABCD-ABCD的棱长为1,线段BD上有两个动点E,F,且EF=1,则下列说法中正确
的是
存在点E,F使得AE∥BF
B.异面直线EF与CD所成的角为6
棱锥B-AEF的体积为定值
D.A到平面AEF的距离为
12.16世纪时,比利时数学家罗门向全世界数学家提出了一个具有挑战性的问题
次方程
95364x-3795x+45x=C的根如何求?
国数学家韦达利用三角知识成功解
决了该问题,并指出当C=2sina时,此方程的全部根为x-2si(
息可得方程x4-45x43+94
95x+4
的根可以是
空题(本大题共4小题,每小题5分,共20分)
3已知长方体的长、宽、高分别为1086(m),则该长方体的外接球的半径R
机器使用总时间X(年)(其中x≥4
)与所需支出的维修总费用(万元)的统计数据如下表:根
据表中数据可得与X之间的线性回归方程为y=0
若该设备维修总费用超过12万元就报废,据此
模型预测该设备最多可使用
年(填整数)
是勾股定理,一个是黄金分割,其中顶角为36°的等腰
三角形被称为“黄金三角形”如图,已知五角星是由5个“黄金三角形”与1个正五
组成
部分的面积为S,正五边形的面积为S
☆
S1
6已知双曲线C
石右顶点为A
交于M,N两点,若OM=2ON(其中O为坐标原点),则双曲线的离心率为
解答題(本大题共6小题,计70分,解答应写出必要的文字说明、证明过程或演算步骤
17、(本小满分10分
在△ABC中,角4,B,C的对边分别为a,,C,△4BC的面积为
1)求B
bc这三个条件中任选一个,补充在上面的问题中
并加以解答.
解答,按第一个解答计
同课章节目录
