华师大版数学八年级下平面直角坐标系课件
文档属性
| 名称 | 华师大版数学八年级下平面直角坐标系课件 |  | |
| 格式 | rar | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-23 21:06:23 | ||
图片预览






文档简介
(共26张PPT)
函数图像(1)
青州市工农子弟学校 崔海利
质以忠信为美 德以好学为机
总结新知
巩固练习
知识回顾
拓展延伸
初二课堂
合作探究
f =
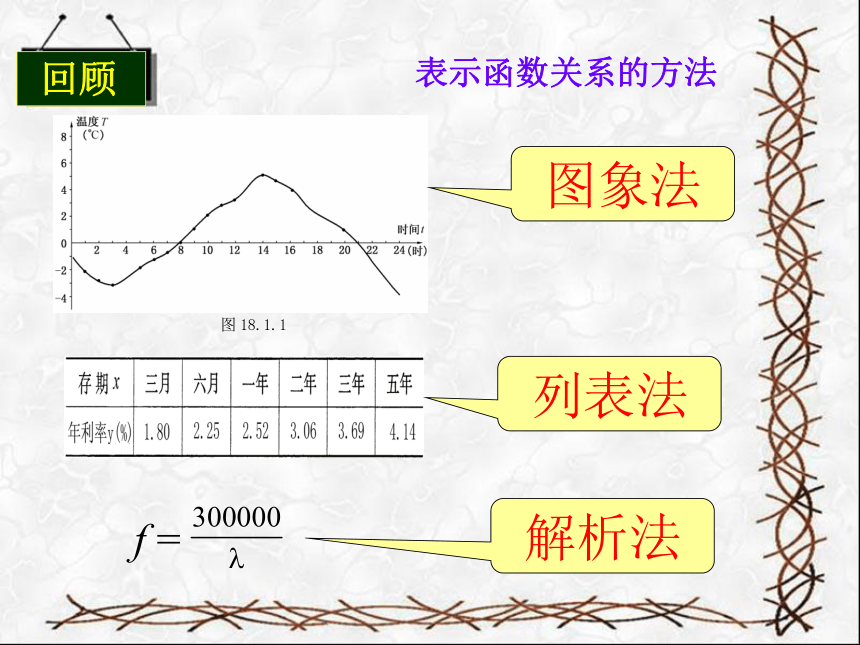
表示函数关系的方法
图象法
解析法
列表法
回顾
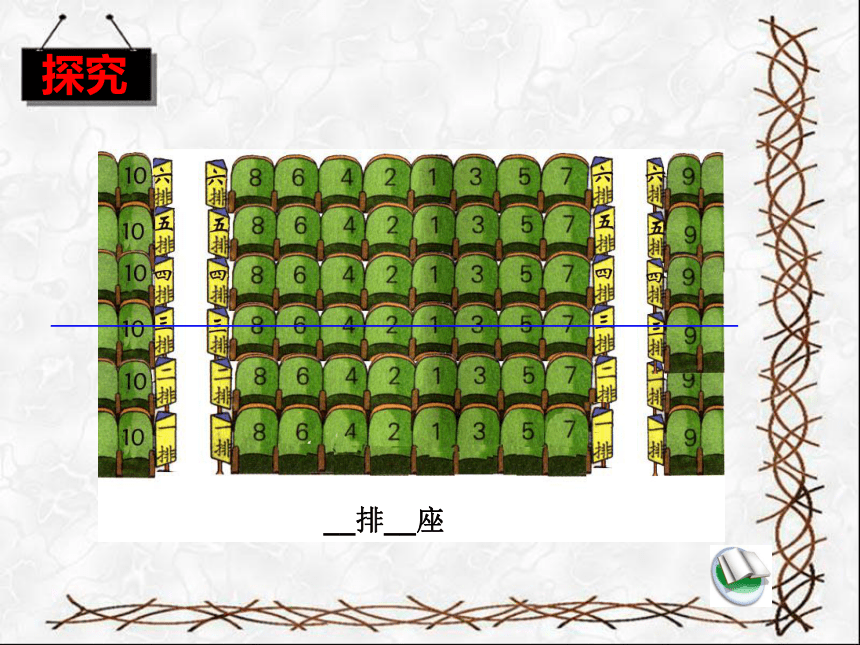
探究
__排__座
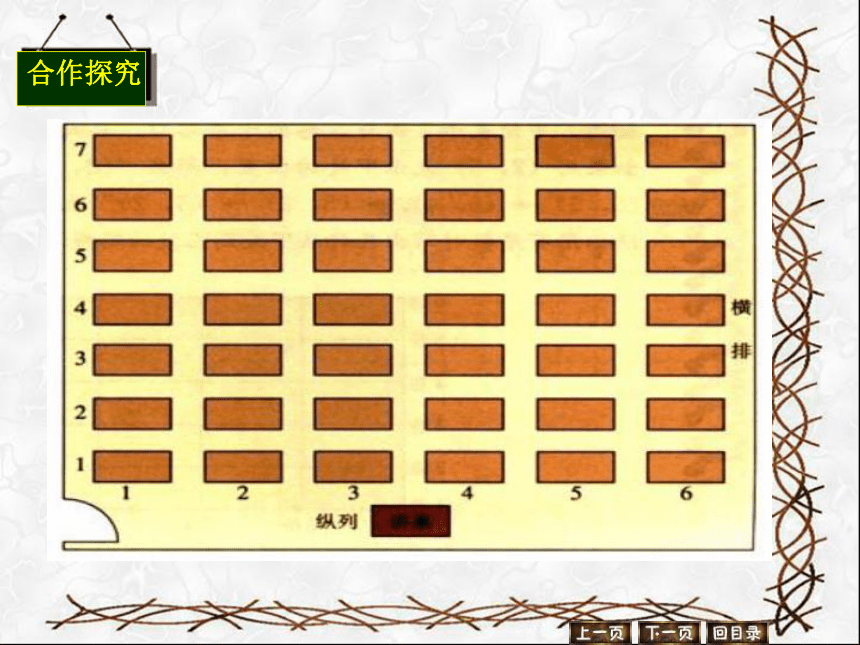
合作探究
探究
想一想:确定一个具体位置至少需要几个数据
2个
回顾
A
x
0
1
2
3
-1
-2
-3
-4
B
A点的坐标是3
B点的坐标是-2
C
C点的坐标是-1
探究
·
·
·
p1
p
p2
背景
法国数学家笛卡儿
最早引入坐标系,用代数方法研究几何图形.笛卡儿是近代科学的始祖。笛卡儿是欧洲近代哲学的奠基人之一,黑格尔称他为“现代哲学之父”。同时,他又是一位勇于探索的科学家,他所建立的解析几何在数学史上具有划时代的意义。
新知
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
坐标原点
第一象限
第四象限
第三象限
第二象限
坐标平面
注意:坐标轴上的点不属于任何象限。
平面直角坐标系
X轴或横轴
y轴或纵轴
新知
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
坐标原点
说一说:平面直角坐标系具有哪些特征呢?
两条数轴:(一般性特征)
(1)互相垂直(通常取向上、向右为正方向)
(2)原点重合
(3)单位长度一般取相同的
X
O
练习:下面四个图形中,是平面直角坐标系的是( )
X
X
Y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
(A)
教程
3 2 1 -1 -2 -3
X
Y
2
1
-1
-2
(B)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
(D)
O
D
新知
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
p
.
M
N
(3,2)
P点的横坐标
P点的纵坐标
P点的坐标
横坐标在前,纵坐标在后,中间用逗号隔开,用小括号括号起来。
·
·
·
p1
p2
(-3,-2)
(-2,1)
(0,0)
练习
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
L
写出图中点L、M、N、U、V、W的坐标。
(-3,1)
(1,3)
(2,-2)
(0,-1)
(3,0)
(-2,-3)
·
·
·
·
·
·
M
U
V
N
W
练习
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
A
.
B
.
.
D
.
C
.
E
F
.
写出图中点A、B、C、D、E、F的坐标。
(-1,2)
(2,1)
(2,-1)
(0,3)
(-2,0)
(-1,-1)
·
·
·
·
·
·
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
B
.
(2,1)
·
·
合作探究
1.在四个象限内的点的坐标有什么特征?
·
(1,2)
第一象限
(+,+)
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
B
(-2,1)
·
·
合作探究
1.在四个象限内的点的坐标有什么特征?
第二象限
(-,+)
(-1,2)
·
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
D
(2,-1)
·
·
合作探究
1.在四个象限内的点的坐标有什么特征?
第三象限
(-,-)
(-1,-1)
第四象限
·
C
·
·
·
(+,-)
总结
1.在四个象限内的点的坐标有什么特征?
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
(+,+)
(+, - )
(- ,+)
( - ,- )
探究总结
2.两条坐标轴上的点的坐标有什么特征?
在Y轴上的点,
它的横坐标为0,
纵坐标为任意实数;
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
·
(-2,0)
F
·
·
·
(0,3)
(2,0)
·
·
·
·
E
(0,-2)
在X轴上的点,
它的纵坐标为0,
横坐标为任意实数;
探究
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
分别描出坐标是(2,3)、 (-2,3)、 (3,-2)
的点Q、S、R。
S
.
.
Q
.
R
·
·
·
Q (2,3)与P (3,2)
是同一点吗?
S (-2,3)与 R (3,-2)
是同一点吗?
·
p
.
新知
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
A
.
B
.
.
D
.
C
.
E
F
.
(-1,2)
(2,1)
(2,-1)
(0,3)
(-2,0)
(-1,-1)
·
·
·
·
·
·
在平面直角坐标系中的点和有序实数对是一一对应的。
在直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴
及原点的对称点,并写出这些点的坐标。
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
A
·
A3
·
A1
·
A2
·
(2,- 3)
(2,3)
(- 2,- 3)
(- 2,3)
观察讨论:关于x轴对称的两点的坐标之间有什么关系?
关于y轴对称的两点的坐标之间有什么关系?
关于原点对称的两点的坐标之间有什么关系?
拓展延伸
总结
对称点的坐标有什么特征?
关于X轴对称的两点,它们的横坐标相同,纵坐标互为相反数;
关于y轴对称的两点,它们的纵坐标相同,横坐标互为相反数;
关于原点对称的两点,它们的横坐标和纵坐标都互为相反数;
认识了平面直角坐标系
根据点的坐标找出的位置;
由点的位置确定它的坐标。
平面直角坐标系中的点
与有序实数对是一一对应的
知识回顾
平面直角坐标系中的点
的特征
函数图像(1)
青州市工农子弟学校 崔海利
质以忠信为美 德以好学为机
总结新知
巩固练习
知识回顾
拓展延伸
初二课堂
合作探究
f =
表示函数关系的方法
图象法
解析法
列表法
回顾
探究
__排__座
合作探究
探究
想一想:确定一个具体位置至少需要几个数据
2个
回顾
A
x
0
1
2
3
-1
-2
-3
-4
B
A点的坐标是3
B点的坐标是-2
C
C点的坐标是-1
探究
·
·
·
p1
p
p2
背景
法国数学家笛卡儿
最早引入坐标系,用代数方法研究几何图形.笛卡儿是近代科学的始祖。笛卡儿是欧洲近代哲学的奠基人之一,黑格尔称他为“现代哲学之父”。同时,他又是一位勇于探索的科学家,他所建立的解析几何在数学史上具有划时代的意义。
新知
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
y
坐标原点
第一象限
第四象限
第三象限
第二象限
坐标平面
注意:坐标轴上的点不属于任何象限。
平面直角坐标系
X轴或横轴
y轴或纵轴
新知
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
坐标原点
说一说:平面直角坐标系具有哪些特征呢?
两条数轴:(一般性特征)
(1)互相垂直(通常取向上、向右为正方向)
(2)原点重合
(3)单位长度一般取相同的
X
O
练习:下面四个图形中,是平面直角坐标系的是( )
X
X
Y
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
(A)
教程
3 2 1 -1 -2 -3
X
Y
2
1
-1
-2
(B)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
(C)
O
-3 -2 -1 1 2 3
3
2
1
-1
-2
-3
Y
(D)
O
D
新知
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
p
.
M
N
(3,2)
P点的横坐标
P点的纵坐标
P点的坐标
横坐标在前,纵坐标在后,中间用逗号隔开,用小括号括号起来。
·
·
·
p1
p2
(-3,-2)
(-2,1)
(0,0)
练习
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
L
写出图中点L、M、N、U、V、W的坐标。
(-3,1)
(1,3)
(2,-2)
(0,-1)
(3,0)
(-2,-3)
·
·
·
·
·
·
M
U
V
N
W
练习
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
A
.
B
.
.
D
.
C
.
E
F
.
写出图中点A、B、C、D、E、F的坐标。
(-1,2)
(2,1)
(2,-1)
(0,3)
(-2,0)
(-1,-1)
·
·
·
·
·
·
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
B
.
(2,1)
·
·
合作探究
1.在四个象限内的点的坐标有什么特征?
·
(1,2)
第一象限
(+,+)
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
B
(-2,1)
·
·
合作探究
1.在四个象限内的点的坐标有什么特征?
第二象限
(-,+)
(-1,2)
·
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
D
(2,-1)
·
·
合作探究
1.在四个象限内的点的坐标有什么特征?
第三象限
(-,-)
(-1,-1)
第四象限
·
C
·
·
·
(+,-)
总结
1.在四个象限内的点的坐标有什么特征?
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
(+,+)
(+, - )
(- ,+)
( - ,- )
探究总结
2.两条坐标轴上的点的坐标有什么特征?
在Y轴上的点,
它的横坐标为0,
纵坐标为任意实数;
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
·
(-2,0)
F
·
·
·
(0,3)
(2,0)
·
·
·
·
E
(0,-2)
在X轴上的点,
它的纵坐标为0,
横坐标为任意实数;
探究
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
分别描出坐标是(2,3)、 (-2,3)、 (3,-2)
的点Q、S、R。
S
.
.
Q
.
R
·
·
·
Q (2,3)与P (3,2)
是同一点吗?
S (-2,3)与 R (3,-2)
是同一点吗?
·
p
.
新知
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
A
.
B
.
.
D
.
C
.
E
F
.
(-1,2)
(2,1)
(2,-1)
(0,3)
(-2,0)
(-1,-1)
·
·
·
·
·
·
在平面直角坐标系中的点和有序实数对是一一对应的。
在直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴
及原点的对称点,并写出这些点的坐标。
x
y
O
1
2
3
- 1
- 2
- 3
1
2
3
- 1
- 2
- 3
A
·
A3
·
A1
·
A2
·
(2,- 3)
(2,3)
(- 2,- 3)
(- 2,3)
观察讨论:关于x轴对称的两点的坐标之间有什么关系?
关于y轴对称的两点的坐标之间有什么关系?
关于原点对称的两点的坐标之间有什么关系?
拓展延伸
总结
对称点的坐标有什么特征?
关于X轴对称的两点,它们的横坐标相同,纵坐标互为相反数;
关于y轴对称的两点,它们的纵坐标相同,横坐标互为相反数;
关于原点对称的两点,它们的横坐标和纵坐标都互为相反数;
认识了平面直角坐标系
根据点的坐标找出的位置;
由点的位置确定它的坐标。
平面直角坐标系中的点
与有序实数对是一一对应的
知识回顾
平面直角坐标系中的点
的特征
