人教八下数学第17章 勾股定理 授课教案(5课时)
文档属性
| 名称 | 人教八下数学第17章 勾股定理 授课教案(5课时) | 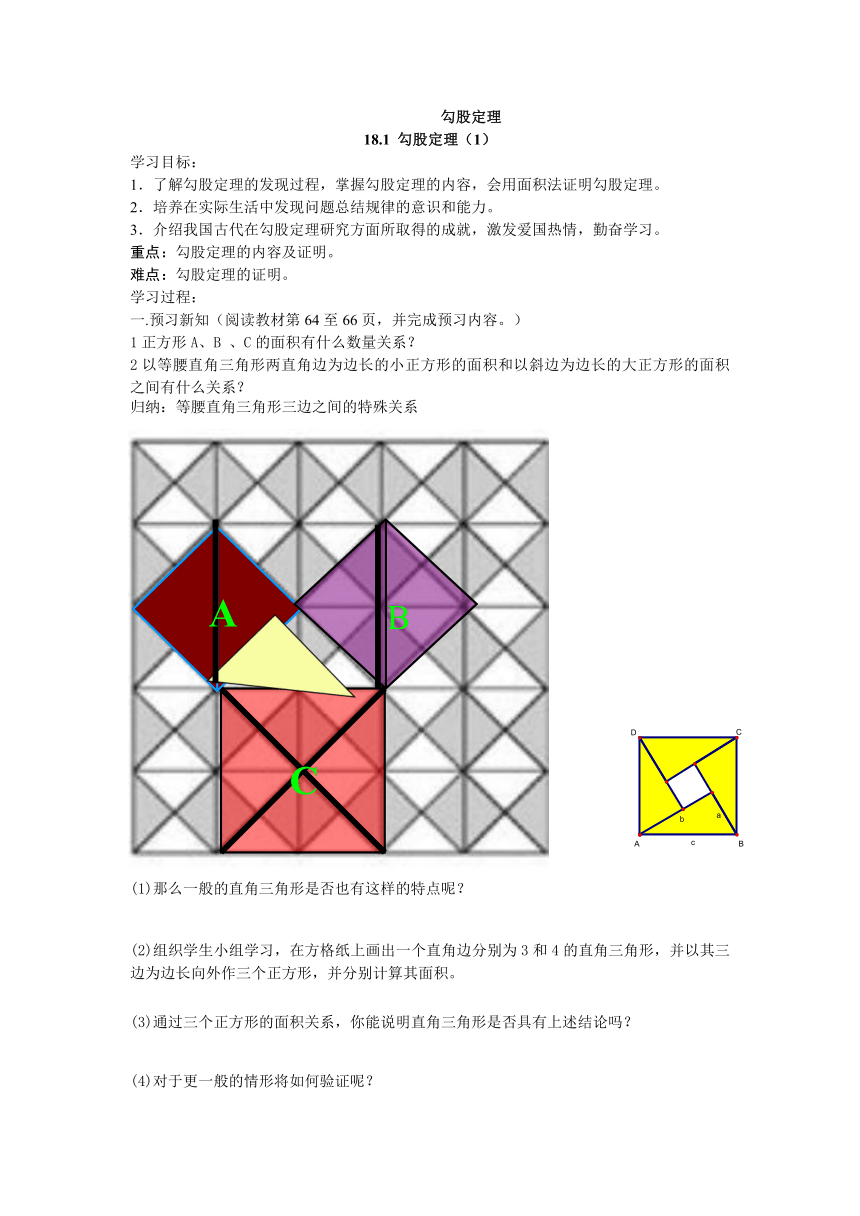 | |
| 格式 | zip | ||
| 文件大小 | 385.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 13:38:39 | ||
图片预览





文档简介
勾股定理
18.1
勾股定理(1)
学习目标:
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
3.介绍我国古代在勾股定理研究方面所取得的成就,激发爱国热情,勤奋学习。
重点:勾股定理的内容及证明。
难点:勾股定理的证明。
学习过程:
一.预习新知(阅读教材第64至66页,并完成预习内容。)
1正方形A、B
、C的面积有什么数量关系?
2以等腰直角三角形两直角边为边长的小正方形的面积和以斜边为边长的大正方形的面积之间有什么关系?
归纳:等腰直角三角形三边之间的特殊关系
(1)那么一般的直角三角形是否也有这样的特点呢?
(2)组织学生小组学习,在方格纸上画出一个直角边分别为3和4的直角三角形,并以其三边为边长向外作三个正方形,并分别计算其面积。
(3)通过三个正方形的面积关系,你能说明直角三角形是否具有上述结论吗?
(4)对于更一般的情形将如何验证呢?
二.课堂展示
方法一;
如图,让学生剪4个全等的直角三角形,拼成如图图形,利用面积证明。
S正方形=_______________=____________________
方法二;
已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证:a2+b2=c2。
分析:左右两边的正方形边长相等,则两个正方形的面积相等。
左边S=______________
右边S=_______________
左边和右边面积相等,
即
化简可得。
方法三:
以a、b
为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab.
把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.
∵
RtΔEAD
≌
RtΔCBE,
∴
∠ADE
=
∠BEC.
∵
∠AED
+
∠ADE
=
90?,
∴
∠AED
+
∠BEC
=
90?.
∴
∠DEC
=
180?―90?=
90?.
∴
ΔDEC是一个等腰直角三角形,
它的面积等于c2.
又∵
∠DAE
=
90?,
∠EBC
=
90?,
∴
AD∥BC.
∴
ABCD是一个直角梯形,它的面积等于_________________
归纳:勾股定理的具体内容是
。
三.随堂练习
1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
⑴两锐角之间的关系:
;
(2)若∠B=30°,则∠B的对边和斜边:
;
(3)三边之间的关系:
2.完成书上P69习题1、2
四.课堂检测新课
标
第
一
网
1.在Rt△ABC中,∠C=90°
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC
=________。
2.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c=
。(已知a、b,求c)
⑵a=
。(已知b、c,求a)
⑶b=
。(已知a、c,求b)
3.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
4.已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A、25
B、14
C、7
D、7或25
5.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56
B、48
C、40
D、32
五.小结与反思
18.1
勾股定理(2)
学习目标:
1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
3.经历探究勾股定理在实际问题中的应用过程,感受勾股定理的应用方法。
4.培养思维意识,发展数学理念,体会勾股定理的应用价值。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
一.预习新知(阅读教材第66至67页,并完成预习内容。)
1.①在解决问题时,每个直角三角形需知道几个条件?
②直角三角形中哪条边最长?
2.在长方形ABCD中,宽AB为1m,长BC为2m
,求AC长.
问题(1)在长方形ABCD中AB、BC、AC大小关系?
(2)一个门框的尺寸如图1所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
图1
二.课堂展示
例:如图2,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
①求梯子的底端B距墙角O多少米?
②如果梯的顶端A沿墙下滑0.5米至C.
算一算,底端滑动的距离近似值(结果保留两位小数).
三.随堂练习
1.书上P68练习1、2
2.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是
米。
3.如图,山坡上两株树木之间的坡面距离是米,则这两株树之间的垂直距离是
米,水平距离是
米。
3题图
四.课堂检测
1.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是
。
1题图
2.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?
2题图
3.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,
∠B=60°,则江面的宽度为
。
4.有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为
米。
5.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ=
厘米。
6.如图3,分别以Rt
△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式
.
变式:书上P71
-11题如图4.
五.小结与反思
18.1
勾股定理(3)
学习目标:
1、能利用勾股定理,根据已知直角三角形的两边长求第三条边长;并在数轴上表示无理数。
2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。
3、培养数形结合的数学思想,并积极参与交流,并积极发表意见。
重点:利用勾股定理在数轴上表示无理数。
难点:确定以无理数为斜边的直角三角形的两条直角边长。
一.预习新知(阅读教材第67至68页,并完成预习内容。)
1.探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
2.分析:如果能画出长为_______的线段,就能在数轴上画出表示的点。容易知道,长为的线段是两条直角边都为______的直角边的斜边。长为的线段能是直角边为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,长为的线段是直角边为正整数_____、
______的直角三角形的斜边。
3.作法:在数轴上找到点A,使OA=_____,作直线垂直于OA,在上取点B,使AB=_____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点。
4.在数轴上画出表示的点?(尺规作图)
二.课堂展示
例1已知直角三角形的两边长分别为5和12,求第三边。
例2已知:如图,等边△ABC的边长是6cm。
⑴求等边△ABC的高。
⑵求S△ABC。
三.随堂练习
1.完成书上P71第9题
2.填空题
⑴在Rt△ABC,∠C=90°,a=8,b=15,则c=
。
⑵在Rt△ABC,∠B=90°,a=3,b=4,则c=
。
⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,则a=
,b=
。
(4)已知直角三角形的两边长分别为3cm和5cm,,则第三边长为
。
2.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形面积。
四.课堂检测
1.已知直角三角形中30°角所对的直角边长是cm,则另一条直角边的长是(
)A.
4cm
B.
cm
C.
6cm
D.
cm
2.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42
B.32
C.42
或
32
D.37
或
33
3.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动(
)
A.
9分米 B.
15分米 C.
5分米
D.
8分米
4.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
5.
等腰△ABC的腰长AB=10cm,底BC为16cm,则底边上的高为
,面积为
.
6.
一个直角三角形的三边为三个连续偶数,则它的三边长分别为
.
7.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,
AB⊥AC,∠B=60°,CD=1cm,求BC的长。
五.小结与反思
18.2
勾股定理的逆定理(一)
学习目标
1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.探究勾股定理的逆定理的证明方法。
3.理解原命题、逆命题、逆定理的概念及关系。
重点:掌握勾股定理的逆定理及简单应用。
难点:勾股定理的逆定理的证明。
一.预习新知(阅读教材P73
—
75
,
完成课前预习)
1.三边长度分别为3
cm、4
cm、5
cm的三角形与以3
cm、4
cm为直角边的直角三角形之间有什么关系?你是怎样得到的?
2.你能证明以6cm、8cm、10cm为三边长的三角形是直角三角形吗?
3.如图18.2-2,若△ABC的三边长、、满足,试证明△ABC是直角三角形,请简要地写出证明过程.
4.此定理与勾股定理之间有怎样的关系?
(1)什么叫互为逆命题
(2)什么叫互为逆定理
(3)任何一个命题都有
_____,但任何一个定理未必都有
__
5.说出下列命题的逆命题。这些命题的逆命题成立吗?
两直线平行,内错角相等;
如果两个实数相等,那么它们的绝对值相等;
全等三角形的对应角相等;
角的内部到角的两边距离相等的点在角的平分线上。
二.课堂展示
例1:判断由线段、、组成的三角形是不是直角三角形:
(1);
(2).
(3);
(4);
三.随堂练习
1.完成书上P75练习1、2
2.如果三条线段长a,b,c满足,这三条线段组成的三角形是不是直角三角形?为什么?
3.A,B,C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
4.思考:我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗?一般地,如果a、b、c是一组勾股数,那么ak、bk、ck(k是正整数)也是一组勾股数吗?
四.课堂检测
1.若△ABC的三边a,b,c满足条件a2+b2+c2+338=10a+24b+26c,试判定△ABC的形状.
2.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为多少米?此三角形的形状为?
3.已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD。
求证:△ABC是直角三角形。
五.小结与反思
18.2勾股定理逆定理(2)
学习目标:
1.进一步掌握勾股定理的逆定理,并会应用勾股定理的逆定理判断一个三角形是否是直角三角形,能够理解勾股定理及其逆定理的区别与联系,掌握它们的应用范围。
2.培养逻辑推理能力,体会“形”与“数”的结合。
3.在不同条件、不同环境中反复运用定理,达到熟练使用,灵活运用的程度。
4.培养数学思维以及合情推理意识,感悟勾股定理和逆定理的应用价值。
重点:勾股定理的逆定理
难点:勾股定理的逆定理的应用
一.预习新知
已知:如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3。
求:四边形ABCD的面积。
归纳:求不规则图形的面积时,要把不规则图形
二.课堂展示
例1.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例2.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
三.随堂练习
1.完成书上P76练习3
2.一个三角形三边之比为3:4:5,则这个三角形三边上的高值比为
A
3:4:5
B
5:4:3
C
20:15:12
D
10:8:2
3.如果△ABC的三边a,b,c满足关系式
+(b-18)2+=0则△ABC是
_______三角形。
四.课堂检测
1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是(
)
A.等腰三角形;
B.直角三角形;
C.等腰三角形或直角三角形;
D.等腰直角三角形。
2.若△ABC的三边a、b、c,满足a:b:c=1:1:,试判断△ABC的形状。
3.已知:如图,四边形ABCD,AB=1,BC=,CD=,AD=3,且AB⊥BC。
求:四边形ABCD的面积。
4.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是
。
5.一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
6.已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状。
7.如图,在正方形ABCD中,F为DC的中点,E为BC上一点且EC=BC,求证:∠EFA=90。.
五.小结与反思
18.1
勾股定理(1)
学习目标:
1.了解勾股定理的发现过程,掌握勾股定理的内容,会用面积法证明勾股定理。
2.培养在实际生活中发现问题总结规律的意识和能力。
3.介绍我国古代在勾股定理研究方面所取得的成就,激发爱国热情,勤奋学习。
重点:勾股定理的内容及证明。
难点:勾股定理的证明。
学习过程:
一.预习新知(阅读教材第64至66页,并完成预习内容。)
1正方形A、B
、C的面积有什么数量关系?
2以等腰直角三角形两直角边为边长的小正方形的面积和以斜边为边长的大正方形的面积之间有什么关系?
归纳:等腰直角三角形三边之间的特殊关系
(1)那么一般的直角三角形是否也有这样的特点呢?
(2)组织学生小组学习,在方格纸上画出一个直角边分别为3和4的直角三角形,并以其三边为边长向外作三个正方形,并分别计算其面积。
(3)通过三个正方形的面积关系,你能说明直角三角形是否具有上述结论吗?
(4)对于更一般的情形将如何验证呢?
二.课堂展示
方法一;
如图,让学生剪4个全等的直角三角形,拼成如图图形,利用面积证明。
S正方形=_______________=____________________
方法二;
已知:在△ABC中,∠C=90°,∠A、∠B、∠C的对边为a、b、c。
求证:a2+b2=c2。
分析:左右两边的正方形边长相等,则两个正方形的面积相等。
左边S=______________
右边S=_______________
左边和右边面积相等,
即
化简可得。
方法三:
以a、b
为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab.
把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.
∵
RtΔEAD
≌
RtΔCBE,
∴
∠ADE
=
∠BEC.
∵
∠AED
+
∠ADE
=
90?,
∴
∠AED
+
∠BEC
=
90?.
∴
∠DEC
=
180?―90?=
90?.
∴
ΔDEC是一个等腰直角三角形,
它的面积等于c2.
又∵
∠DAE
=
90?,
∠EBC
=
90?,
∴
AD∥BC.
∴
ABCD是一个直角梯形,它的面积等于_________________
归纳:勾股定理的具体内容是
。
三.随堂练习
1.如图,直角△ABC的主要性质是:∠C=90°,(用几何语言表示)
⑴两锐角之间的关系:
;
(2)若∠B=30°,则∠B的对边和斜边:
;
(3)三边之间的关系:
2.完成书上P69习题1、2
四.课堂检测新课
标
第
一
网
1.在Rt△ABC中,∠C=90°
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=__________;
④若a∶b=3∶4,c=10则SRt△ABC
=________。
2.已知在Rt△ABC中,∠B=90°,a、b、c是△ABC的三边,则
⑴c=
。(已知a、b,求c)
⑵a=
。(已知b、c,求a)
⑶b=
。(已知a、c,求b)
3.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。
4.已知一个Rt△的两边长分别为3和4,则第三边长的平方是( )
A、25
B、14
C、7
D、7或25
5.等腰三角形底边上的高为8,周长为32,则三角形的面积为( )
A、56
B、48
C、40
D、32
五.小结与反思
18.1
勾股定理(2)
学习目标:
1.会用勾股定理解决简单的实际问题。
2.树立数形结合的思想。
3.经历探究勾股定理在实际问题中的应用过程,感受勾股定理的应用方法。
4.培养思维意识,发展数学理念,体会勾股定理的应用价值。
重点:勾股定理的应用。
难点:实际问题向数学问题的转化。
一.预习新知(阅读教材第66至67页,并完成预习内容。)
1.①在解决问题时,每个直角三角形需知道几个条件?
②直角三角形中哪条边最长?
2.在长方形ABCD中,宽AB为1m,长BC为2m
,求AC长.
问题(1)在长方形ABCD中AB、BC、AC大小关系?
(2)一个门框的尺寸如图1所示.
①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?
②若薄木板长3米,宽1.5米呢?
③若薄木板长3米,宽2.2米呢?为什么?
图1
二.课堂展示
例:如图2,一个3米长的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.
①求梯子的底端B距墙角O多少米?
②如果梯的顶端A沿墙下滑0.5米至C.
算一算,底端滑动的距离近似值(结果保留两位小数).
三.随堂练习
1.书上P68练习1、2
2.小明和爸爸妈妈十一登香山,他们沿着45度的坡路走了500米,看到了一棵红叶树,这棵红叶树的离地面的高度是
米。
3.如图,山坡上两株树木之间的坡面距离是米,则这两株树之间的垂直距离是
米,水平距离是
米。
3题图
四.课堂检测
1.如图,一根12米高的电线杆两侧各用15米的铁丝固定,两个固定点之间的距离是
。
1题图
2.如图,原计划从A地经C地到B地修建一条高速公路,后因技术攻关,可以打隧道由A地到B地直接修建,已知高速公路一公里造价为300万元,隧道总长为2公里,隧道造价为500万元,AC=80公里,BC=60公里,则改建后可省工程费用是多少?
2题图
3.如图,欲测量松花江的宽度,沿江岸取B、C两点,在江对岸取一点A,使AC垂直江岸,测得BC=50米,
∠B=60°,则江面的宽度为
。
4.有一个边长为1米正方形的洞口,想用一个圆形盖去盖住这个洞口,则圆形盖半径至少为
米。
5.一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ=
厘米。
6.如图3,分别以Rt
△ABC三边为边向外作三个正方形,其面积分别用S1、S2、S3表示,容易得出S1、S2、S3之间有的关系式
.
变式:书上P71
-11题如图4.
五.小结与反思
18.1
勾股定理(3)
学习目标:
1、能利用勾股定理,根据已知直角三角形的两边长求第三条边长;并在数轴上表示无理数。
2、体会数与形的密切联系,增强应用意识,提高运用勾股定理解决问题的能力。
3、培养数形结合的数学思想,并积极参与交流,并积极发表意见。
重点:利用勾股定理在数轴上表示无理数。
难点:确定以无理数为斜边的直角三角形的两条直角边长。
一.预习新知(阅读教材第67至68页,并完成预习内容。)
1.探究:我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示的点吗?
2.分析:如果能画出长为_______的线段,就能在数轴上画出表示的点。容易知道,长为的线段是两条直角边都为______的直角边的斜边。长为的线段能是直角边为正整数的直角三角形的斜边吗?
利用勾股定理,可以发现,长为的线段是直角边为正整数_____、
______的直角三角形的斜边。
3.作法:在数轴上找到点A,使OA=_____,作直线垂直于OA,在上取点B,使AB=_____,以原点O为圆心,以OB为半径作弧,弧与数轴的交点C即为表示的点。
4.在数轴上画出表示的点?(尺规作图)
二.课堂展示
例1已知直角三角形的两边长分别为5和12,求第三边。
例2已知:如图,等边△ABC的边长是6cm。
⑴求等边△ABC的高。
⑵求S△ABC。
三.随堂练习
1.完成书上P71第9题
2.填空题
⑴在Rt△ABC,∠C=90°,a=8,b=15,则c=
。
⑵在Rt△ABC,∠B=90°,a=3,b=4,则c=
。
⑶在Rt△ABC,∠C=90°,c=10,a:b=3:4,则a=
,b=
。
(4)已知直角三角形的两边长分别为3cm和5cm,,则第三边长为
。
2.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形面积。
四.课堂检测
1.已知直角三角形中30°角所对的直角边长是cm,则另一条直角边的长是(
)A.
4cm
B.
cm
C.
6cm
D.
cm
2.△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42
B.32
C.42
或
32
D.37
或
33
3.一架25分米长的梯子,斜立在一竖直的墙上,这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米,那么梯足将滑动(
)
A.
9分米 B.
15分米 C.
5分米
D.
8分米
4.
如图,学校有一块长方形花铺,有极少数人为了避开拐角走“捷径”,在花铺内走出了一条“路”.他们仅仅少走了
步路(假设2步为1米),却踩伤了花草.
5.
等腰△ABC的腰长AB=10cm,底BC为16cm,则底边上的高为
,面积为
.
6.
一个直角三角形的三边为三个连续偶数,则它的三边长分别为
.
7.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC,
AB⊥AC,∠B=60°,CD=1cm,求BC的长。
五.小结与反思
18.2
勾股定理的逆定理(一)
学习目标
1.体会勾股定理的逆定理得出过程,掌握勾股定理的逆定理。
2.探究勾股定理的逆定理的证明方法。
3.理解原命题、逆命题、逆定理的概念及关系。
重点:掌握勾股定理的逆定理及简单应用。
难点:勾股定理的逆定理的证明。
一.预习新知(阅读教材P73
—
75
,
完成课前预习)
1.三边长度分别为3
cm、4
cm、5
cm的三角形与以3
cm、4
cm为直角边的直角三角形之间有什么关系?你是怎样得到的?
2.你能证明以6cm、8cm、10cm为三边长的三角形是直角三角形吗?
3.如图18.2-2,若△ABC的三边长、、满足,试证明△ABC是直角三角形,请简要地写出证明过程.
4.此定理与勾股定理之间有怎样的关系?
(1)什么叫互为逆命题
(2)什么叫互为逆定理
(3)任何一个命题都有
_____,但任何一个定理未必都有
__
5.说出下列命题的逆命题。这些命题的逆命题成立吗?
两直线平行,内错角相等;
如果两个实数相等,那么它们的绝对值相等;
全等三角形的对应角相等;
角的内部到角的两边距离相等的点在角的平分线上。
二.课堂展示
例1:判断由线段、、组成的三角形是不是直角三角形:
(1);
(2).
(3);
(4);
三.随堂练习
1.完成书上P75练习1、2
2.如果三条线段长a,b,c满足,这三条线段组成的三角形是不是直角三角形?为什么?
3.A,B,C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
4.思考:我们知道3、4、5是一组勾股数,那么3k、4k、5k(k是正整数)也是一组勾股数吗?一般地,如果a、b、c是一组勾股数,那么ak、bk、ck(k是正整数)也是一组勾股数吗?
四.课堂检测
1.若△ABC的三边a,b,c满足条件a2+b2+c2+338=10a+24b+26c,试判定△ABC的形状.
2.一根24米绳子,折成三边为三个连续偶数的三角形,则三边长分别为多少米?此三角形的形状为?
3.已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD。
求证:△ABC是直角三角形。
五.小结与反思
18.2勾股定理逆定理(2)
学习目标:
1.进一步掌握勾股定理的逆定理,并会应用勾股定理的逆定理判断一个三角形是否是直角三角形,能够理解勾股定理及其逆定理的区别与联系,掌握它们的应用范围。
2.培养逻辑推理能力,体会“形”与“数”的结合。
3.在不同条件、不同环境中反复运用定理,达到熟练使用,灵活运用的程度。
4.培养数学思维以及合情推理意识,感悟勾股定理和逆定理的应用价值。
重点:勾股定理的逆定理
难点:勾股定理的逆定理的应用
一.预习新知
已知:如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3。
求:四边形ABCD的面积。
归纳:求不规则图形的面积时,要把不规则图形
二.课堂展示
例1.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
例2.如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
三.随堂练习
1.完成书上P76练习3
2.一个三角形三边之比为3:4:5,则这个三角形三边上的高值比为
A
3:4:5
B
5:4:3
C
20:15:12
D
10:8:2
3.如果△ABC的三边a,b,c满足关系式
+(b-18)2+=0则△ABC是
_______三角形。
四.课堂检测
1.若△ABC的三边a、b、c,满足(a-b)(a2+b2-c2)=0,则△ABC是(
)
A.等腰三角形;
B.直角三角形;
C.等腰三角形或直角三角形;
D.等腰直角三角形。
2.若△ABC的三边a、b、c,满足a:b:c=1:1:,试判断△ABC的形状。
3.已知:如图,四边形ABCD,AB=1,BC=,CD=,AD=3,且AB⊥BC。
求:四边形ABCD的面积。
4.小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是
。
5.一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
6.已知△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状。
7.如图,在正方形ABCD中,F为DC的中点,E为BC上一点且EC=BC,求证:∠EFA=90。.
五.小结与反思
