五年级上册数学教案-组合图形的面积 北师大版
文档属性
| 名称 | 五年级上册数学教案-组合图形的面积 北师大版 |

|
|
| 格式 | doc | ||
| 文件大小 | 61.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览


文档简介
组合图形的面积
教学设计
教学内容:
北师大版小学数学五年级上册第6单元“组合图形面积”。
教材分析:
本册教材的第4单元,学生已经学行四边形、三角形与梯形的面积。在此基础上学习组合图形,一方面可以巩固已学的基本图形,另一方面能将所学的知识进行综合,提高学生综合能力。在“组合图形面积”中,重点探索计算组合图形面积的计算方法。由于本单元是小学阶段平面几何直线型内容的最后章节,因此,教材所安排的内容除了巩固学生所学的知识外,更重要的是将解决问题的思考策略渗透其中。
教学目标:
1、在自主探索的活动中,理解计算组合图形面积的多种方法,并渗透转化的数学思想。
2、能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
3、能运用所学的知识,解决生活中组合图形的实际问题。
4、在有效的情境中激发学生学习的兴趣的主动性,培养热爱数学的思想感情。
教学重点:
探索组合图形面积的计算方法。
教学难点:
根据组合图形的条件,有效地选择计算方法。
教学准备:
课件
教学方法:
任务驱动
教学过程:
复习导入
师:这片草地里隐藏了很多我们学过的平面图形,猜一猜可能是什么图形?猜的对不对呢?我们一边看,一边说出它的名称。
师:这些是基本的平面图形。他们的面积公式,你还记得吗?
生:背诵面积公式。
二引入新课。
师:这个图形属于刚刚看过的基本图形吗?那它是一个什么样的图形呢?我们还可以把它看成是由哪些基本图形组成的呢?
生:自由回答
师:我们发现,这个图形可以由几个基本图形组合而成,我们把这样的图形叫组合图形。
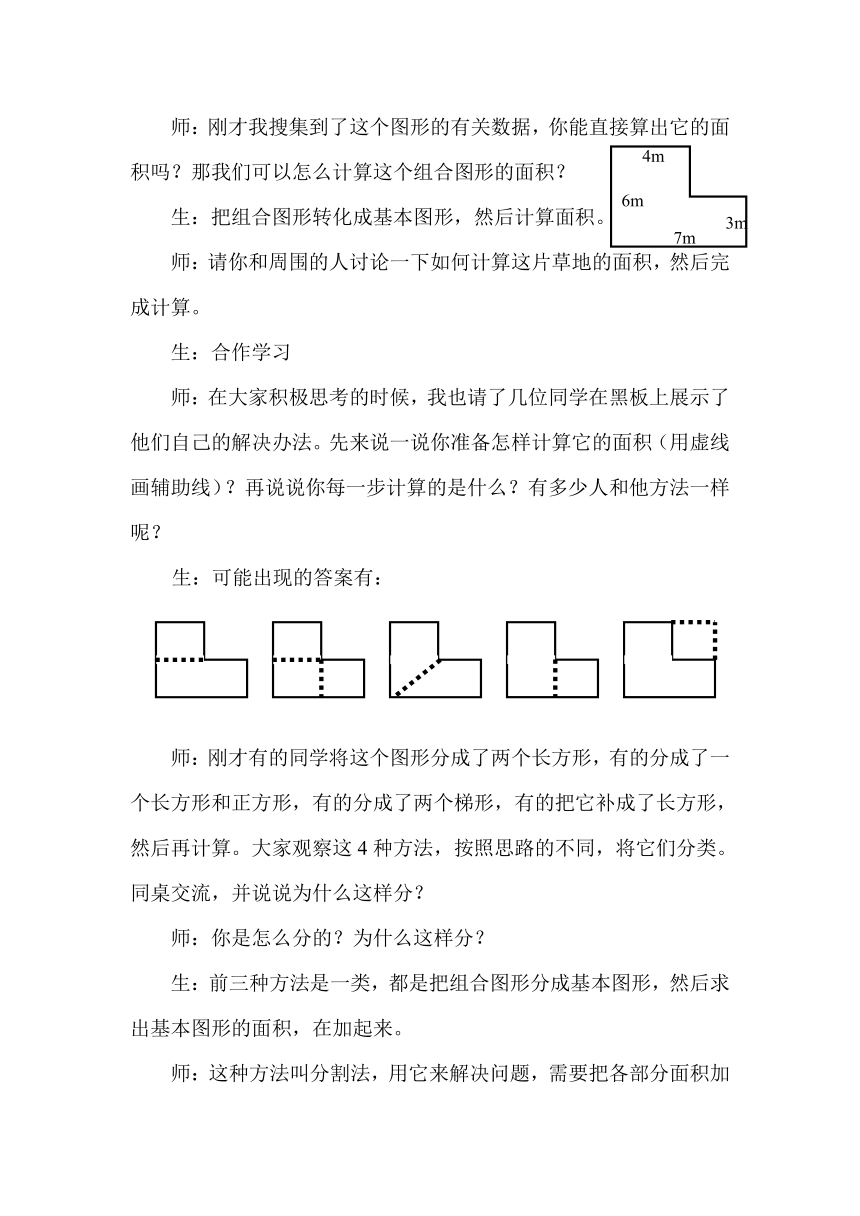
师:刚才我搜集到了这个图形的有关数据,你能直接算出它的面积吗?那我们可以怎么计算这个组合图形的面积?
生:把组合图形转化成基本图形,然后计算面积。
师:请你和周围的人讨论一下如何计算这片草地的面积,然后完成计算。
生:合作学习
师:在大家积极思考的时候,我也请了几位同学在黑板上展示了他们自己的解决办法。先来说一说你准备怎样计算它的面积(用虚线画辅助线)?再说说你每一步计算的是什么?有多少人和他方法一样呢?
生:可能出现的答案有:
师:刚才有的同学将这个图形分成了两个长方形,有的分成了一个长方形和正方形,有的分成了两个梯形,有的把它补成了长方形,然后再计算。大家观察这4种方法,按照思路的不同,将它们分类。同桌交流,并说说为什么这样分?
师:你是怎么分的?为什么这样分?
生:前三种方法是一类,都是把组合图形分成基本图形,然后求出基本图形的面积,在加起来。
师:这种方法叫分割法,用它来解决问题,需要把各部分面积加起来。
生:后一种方法是一类,把组合图形补完整,求出完整图形的面积,在减去补上的面积。
师:这种方法叫添补法,用它来解决问题,需要用大面积减去小面积。
师:还有一种方法是割补法。
师:其实无论是哪种方法,他们的目的都是将组合图形转化成基本图形,从而完成面积计算。这种思想就是转化的思想,是学习数学经常要用到的一个方法。希望同学们在以后的学习中,能够运用转化的思想,把不能解决的问题转化成以前学过的问题,加以解决。
三、练习
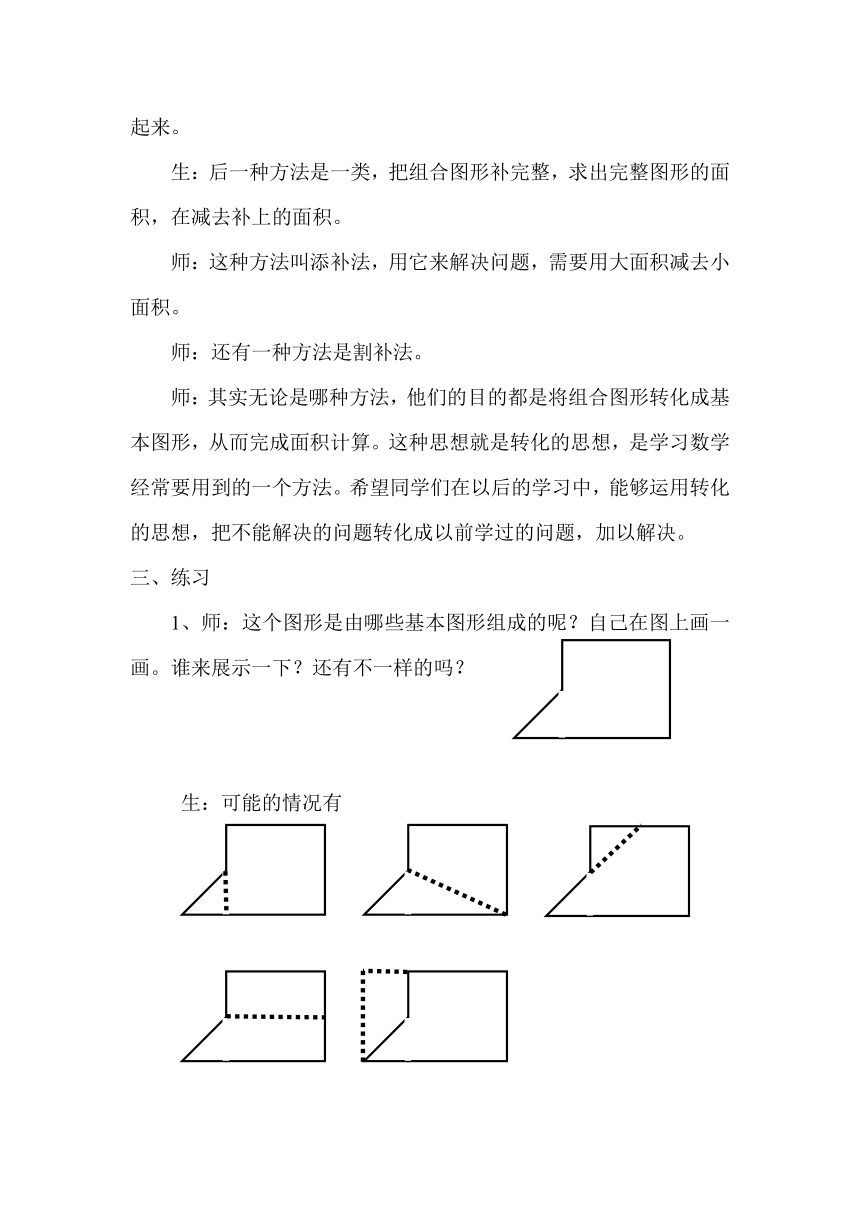
1、师:这个图形是由哪些基本图形组成的呢?自己在图上画一画。谁来展示一下?还有不一样的吗?
生:可能的情况有
师:请你来评价一下这两种方法。
(分成了不是已学过的图形)
(分得过细,数量上过多)
师:想一想,在分割的过程中,怎样才能使你的计算简单呢?
生:分成两个图形的比分成三个图形的要相对简单些;同样分成两个图形的,分成长方形、正方形的比分成梯形、三角形的在计算上相对又要简单些。
师:计算组合图形面积的方法很多,但我们要选择简单的方法。分割的图形越少、越简单,计算就越容易。
2、师:独立计算这个图形的面积
7cm
生:独立完成。
3、师:一个问题,同学生想出了这么多而又简单的方法,真是了不起。下面请看这里。
师:看哪些同学能很快地求出共要多少钱?
反馈:只有一种“补”的解法。
师:看来,求组合图形的面积,并不是所有的方法都可以的,有时,我们还得根据条件选择合适的方法。
四、总结。
学习了这一课,你学会了什么?
教学反思:
《组合图形的面积》这一课,是在学生学习了长方形、正方形、平行四边形、三角形与梯形面积计算的基础上进行展开教学的,本课教学从学生的原有认知水平和思维特点出发,设计了一系列的操作活动,引导学生经历实践、思考问题的探索过程,发展空间观念,提高解决问题的能力。具体体现在以下几个方面:
一、创设情境,激发学习兴趣
让学生用已学的平行四边形、三角形等拼成自己喜欢的图形,让学生体会由几个简单的图形组合而成是组合图形。再观察生活中的组合图形,使学生逐步熟悉组合图形,调动学生的学习兴趣。
二、提供自主探索的空间,感受解题策略、方法的多样性
充分考虑儿童的原有认知水平及儿童心理发展水平,放手让学生自主探究,让学生动手操作、小组交流,亲身经历计算组合图形面积的过程,重视把学生的思维过程充分暴露出来。在自主探索、解决问题中感受解题策略、方法的多样性。
三、在探索中感悟数学思想方法
本节课设计,力求有效渗透转化、优化等数学思想方法。特别是转化的数学思想方法在本节课的各个环节都进行精心的设计,这种思想方法对学生学习数学终身受用。
教学设计
教学内容:
北师大版小学数学五年级上册第6单元“组合图形面积”。
教材分析:
本册教材的第4单元,学生已经学行四边形、三角形与梯形的面积。在此基础上学习组合图形,一方面可以巩固已学的基本图形,另一方面能将所学的知识进行综合,提高学生综合能力。在“组合图形面积”中,重点探索计算组合图形面积的计算方法。由于本单元是小学阶段平面几何直线型内容的最后章节,因此,教材所安排的内容除了巩固学生所学的知识外,更重要的是将解决问题的思考策略渗透其中。
教学目标:
1、在自主探索的活动中,理解计算组合图形面积的多种方法,并渗透转化的数学思想。
2、能根据各种组合图形的条件,有效地选择计算方法并进行正确的解答。
3、能运用所学的知识,解决生活中组合图形的实际问题。
4、在有效的情境中激发学生学习的兴趣的主动性,培养热爱数学的思想感情。
教学重点:
探索组合图形面积的计算方法。
教学难点:
根据组合图形的条件,有效地选择计算方法。
教学准备:
课件
教学方法:
任务驱动
教学过程:
复习导入
师:这片草地里隐藏了很多我们学过的平面图形,猜一猜可能是什么图形?猜的对不对呢?我们一边看,一边说出它的名称。
师:这些是基本的平面图形。他们的面积公式,你还记得吗?
生:背诵面积公式。
二引入新课。
师:这个图形属于刚刚看过的基本图形吗?那它是一个什么样的图形呢?我们还可以把它看成是由哪些基本图形组成的呢?
生:自由回答
师:我们发现,这个图形可以由几个基本图形组合而成,我们把这样的图形叫组合图形。
师:刚才我搜集到了这个图形的有关数据,你能直接算出它的面积吗?那我们可以怎么计算这个组合图形的面积?
生:把组合图形转化成基本图形,然后计算面积。
师:请你和周围的人讨论一下如何计算这片草地的面积,然后完成计算。
生:合作学习
师:在大家积极思考的时候,我也请了几位同学在黑板上展示了他们自己的解决办法。先来说一说你准备怎样计算它的面积(用虚线画辅助线)?再说说你每一步计算的是什么?有多少人和他方法一样呢?
生:可能出现的答案有:
师:刚才有的同学将这个图形分成了两个长方形,有的分成了一个长方形和正方形,有的分成了两个梯形,有的把它补成了长方形,然后再计算。大家观察这4种方法,按照思路的不同,将它们分类。同桌交流,并说说为什么这样分?
师:你是怎么分的?为什么这样分?
生:前三种方法是一类,都是把组合图形分成基本图形,然后求出基本图形的面积,在加起来。
师:这种方法叫分割法,用它来解决问题,需要把各部分面积加起来。
生:后一种方法是一类,把组合图形补完整,求出完整图形的面积,在减去补上的面积。
师:这种方法叫添补法,用它来解决问题,需要用大面积减去小面积。
师:还有一种方法是割补法。
师:其实无论是哪种方法,他们的目的都是将组合图形转化成基本图形,从而完成面积计算。这种思想就是转化的思想,是学习数学经常要用到的一个方法。希望同学们在以后的学习中,能够运用转化的思想,把不能解决的问题转化成以前学过的问题,加以解决。
三、练习
1、师:这个图形是由哪些基本图形组成的呢?自己在图上画一画。谁来展示一下?还有不一样的吗?
生:可能的情况有
师:请你来评价一下这两种方法。
(分成了不是已学过的图形)
(分得过细,数量上过多)
师:想一想,在分割的过程中,怎样才能使你的计算简单呢?
生:分成两个图形的比分成三个图形的要相对简单些;同样分成两个图形的,分成长方形、正方形的比分成梯形、三角形的在计算上相对又要简单些。
师:计算组合图形面积的方法很多,但我们要选择简单的方法。分割的图形越少、越简单,计算就越容易。
2、师:独立计算这个图形的面积
7cm
生:独立完成。
3、师:一个问题,同学生想出了这么多而又简单的方法,真是了不起。下面请看这里。
师:看哪些同学能很快地求出共要多少钱?
反馈:只有一种“补”的解法。
师:看来,求组合图形的面积,并不是所有的方法都可以的,有时,我们还得根据条件选择合适的方法。
四、总结。
学习了这一课,你学会了什么?
教学反思:
《组合图形的面积》这一课,是在学生学习了长方形、正方形、平行四边形、三角形与梯形面积计算的基础上进行展开教学的,本课教学从学生的原有认知水平和思维特点出发,设计了一系列的操作活动,引导学生经历实践、思考问题的探索过程,发展空间观念,提高解决问题的能力。具体体现在以下几个方面:
一、创设情境,激发学习兴趣
让学生用已学的平行四边形、三角形等拼成自己喜欢的图形,让学生体会由几个简单的图形组合而成是组合图形。再观察生活中的组合图形,使学生逐步熟悉组合图形,调动学生的学习兴趣。
二、提供自主探索的空间,感受解题策略、方法的多样性
充分考虑儿童的原有认知水平及儿童心理发展水平,放手让学生自主探究,让学生动手操作、小组交流,亲身经历计算组合图形面积的过程,重视把学生的思维过程充分暴露出来。在自主探索、解决问题中感受解题策略、方法的多样性。
三、在探索中感悟数学思想方法
本节课设计,力求有效渗透转化、优化等数学思想方法。特别是转化的数学思想方法在本节课的各个环节都进行精心的设计,这种思想方法对学生学习数学终身受用。
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
