9.2中心对称与中心对称图形(2)-江苏省新沂市钟吾中学苏科版八年级数学下册导学案(含答案)
文档属性
| 名称 | 9.2中心对称与中心对称图形(2)-江苏省新沂市钟吾中学苏科版八年级数学下册导学案(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 102.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览


文档简介
钟吾中学八年级(下)数学导学案
课题 中心对称与中心对称图形(2) 课型 新授 章节 9.2
时间
课时 第 课时
学习目标:
1.认识中心对称图形,理解中心对称图形的性质,会判别轴对称和中心对称;
2.会应用中心对称的性质解决问题.
学习重点:中心对称性质及其应用
(二)预学成果
1.预学作业:
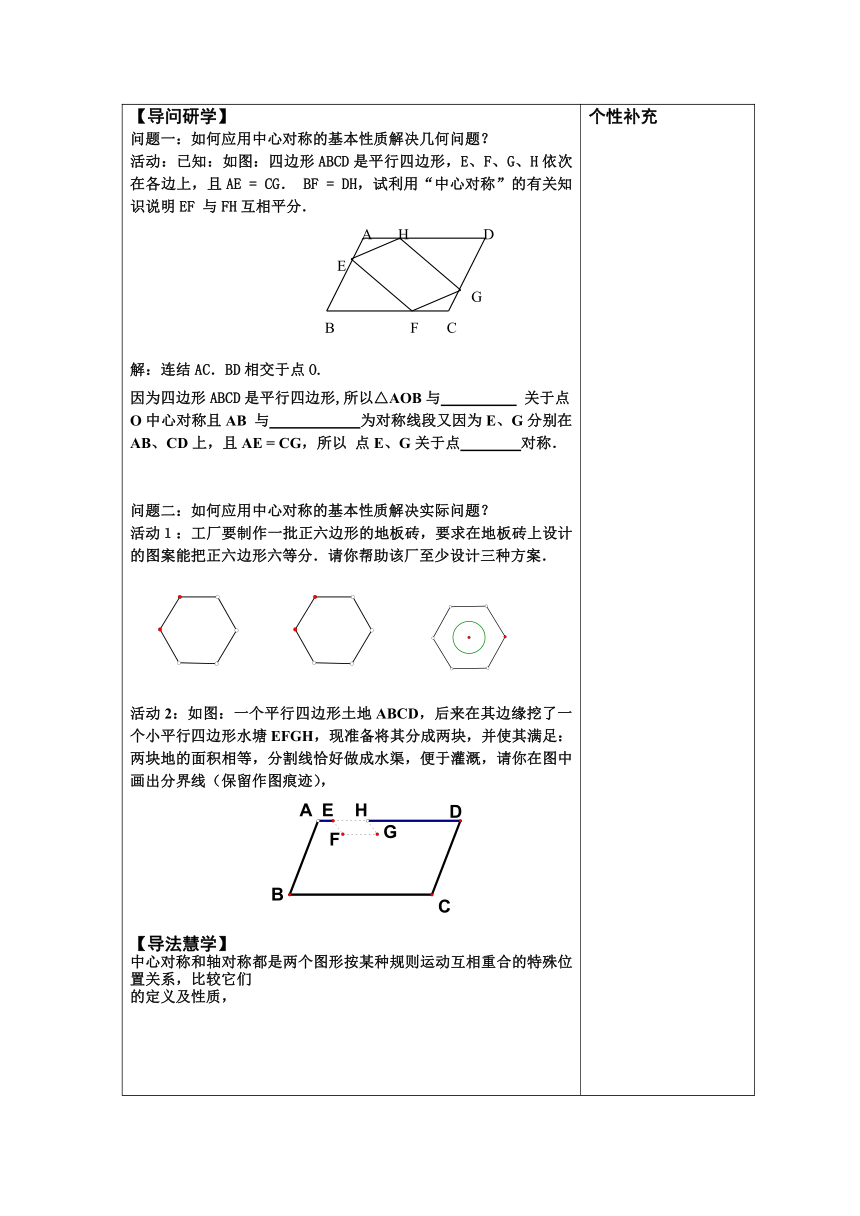
问题:这些图形中,哪些是中心对称图形 ,哪些是轴对称图形
(2)平面内,如果把一个图形 ,那么这个
图形叫做中心对称图形. 就是它的对称中心.两个图形中的 叫做对称点.
2.预学检测:
(1)预习作业1中的四个图案中, 是轴对称图形, 是中心对称图形, 既是中心对称图形又是轴对称图形.
(2)中心对称图形是 个图形的特征,而中心对称是指 图形间的关系.
(3)认一认:下列常见图形哪些是轴对称图形?哪些是中心对称图形?
线段a 等边三角形b 平行四边形c
长方形d 圆形e 直角三角形f
3.预学质疑:对于中心对称与中心对称图形联系与区别的预学,你有哪些疑惑?
个性补充
【导问研学】 问题一:如何应用中心对称的基本性质解决几何问题?
活动:已知:如图:四边形ABCD是平行四边形,E、F、G、H依次在各边上,且AE = CG. BF = DH,试利用“中心对称”的有关知识说明EF 与FH互相平分.
解:连结AC.BD相交于点O.
因为四边形ABCD是平行四边形,所以△AOB与 关于点O中心对称且AB 与 为对称线段又因为E、G分别在AB、CD上,且AE = CG,所以 点E、G关于点 对称.
问题二:如何应用中心对称的基本性质解决实际问题?
活动1:工厂要制作一批正六边形的地板砖,要求在地板砖上设计的图案能把正六边形六等分.请你帮助该厂至少设计三种方案.
活动2:如图:一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线(保留作图痕迹),
【导法慧学】
中心对称和轴对称都是两个图形按某种规则运动互相重合的特殊位置关系,比较它们
的定义及性质,
个性补充
【导评促学】
1.下列图形中,既是轴对称图形,又是中心对称图形的有
2.下列说法正确的是( )
A.中心对称图形不一定是轴对称图形
B.中心对称图形的对称中心不一定唯一
C.轴对称图形一定不是中心对称图形
D.轴对称图形的对称轴不一定唯一
3.已知:AC与BD互相平分于O,E、F分别在AB.CD上,且AE = CF,试利用“中心对称”的有关知识说明:点E、O、F 在同一直线上,且OE= OF
★4.如右图,正方形ABCD和正方形OEFG的边长均为4,点O是正方形ABCD的对称中心,则图中阴影部分的面积为 .
个性补充
教学反思
钟吾中学八年级(下)数学导学案
课题 中心对称与中心对称图形(2) 课型 新授 章节 9.2
时间
课时 第 课时
学习目标:
1.认识中心对称图形,理解中心对称图形的性质,会判别轴对称和中心对称;
2.会应用中心对称的性质解决问题.
学习重点:中心对称性质及其应用
(二)预学成果
1.预学作业:
问题:这些图形中,哪些是中心对称图形 ,哪些是轴对称图形
(2)平面内,如果把一个图形 ,那么这个
图形叫做中心对称图形. 就是它的对称中心.两个图形中的 叫做对称点.
2.预学检测:
(1)预习作业1中的四个图案中, 是轴对称图形, 是中心对称图形, 既是中心对称图形又是轴对称图形.
(2)中心对称图形是 个图形的特征,而中心对称是指 图形间的关系.
(3)认一认:下列常见图形哪些是轴对称图形?哪些是中心对称图形?
线段a 等边三角形b 平行四边形c
长方形d 圆形e 直角三角形f
3.预学质疑:对于中心对称与中心对称图形联系与区别的预学,你有哪些疑惑?
个性补充
中心对称图形:④③②
轴对称图形:①④
绕着某一点旋转180,如果它能与原来的图形重合 这个点 对应点
1 2
轴对称图形:a、b、d、e
中心对称图形:c、d、e
【导问研学】 问题一:如何应用中心对称的基本性质解决几何问题?
活动:已知:如图:四边形ABCD是平行四边形,E、F、G、H依次在各边上,且AE = CG. BF = DH,试利用“中心对称”的有关知识说明EG 与FH互相平分.
解:连结AC.BD相交于点O.
因为四边形ABCD是平行四边形,所以△AOB与 关于点O中心对称且AB 与 为对称线段又因为E、G分别在AB、CD上,且AE = CG,所以 点E、G关于点 对称.
问题二:如何应用中心对称的基本性质解决实际问题?
活动1:工厂要制作一批正六边形的地板砖,要求在地板砖上设计的图案能把正六边形六等分.请你帮助该厂至少设计三种方案.
活动2:如图:一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线(保留作图痕迹),
【导法慧学】
中心对称和轴对称都是两个图形按某种规则运动互相重合的特殊位置关系,比较它们
的定义及性质,
个性补充
△COD CD
点O
充分放手与学生,发挥他们的想象,拓展他们的思维。
【导评促学】
1.下列图形中,既是轴对称图形,又是中心对称图形的有
2.下列说法正确的是( )
A.中心对称图形不一定是轴对称图形
B.中心对称图形的对称中心不一定唯一
C.轴对称图形一定不是中心对称图形
D.轴对称图形的对称轴不一定唯一
3.已知:AC与BD互相平分于O,E、F分别在AB.CD上,且AE = CF,试利用“中心对称”的有关知识说明:点E、O、F 在同一直线上,且OE= OF
★4.如右图,正方形ABCD和正方形OEFG的边长均为4,点O是正方形ABCD的对称中心,则图中阴影部分的面积为 .
个性补充
⑵ ⑷
A
因为AC与BD关于点O中心对称,且AC 与BD 为对称线段又因为E、F分别在AC、BD上,且AE = CF,所以 点E、F关于点O对称.
所以OE= OF
1
先独立完成,互相批阅,找出错误,教师点评。
教学反思
课题 中心对称与中心对称图形(2) 课型 新授 章节 9.2
时间
课时 第 课时
学习目标:
1.认识中心对称图形,理解中心对称图形的性质,会判别轴对称和中心对称;
2.会应用中心对称的性质解决问题.
学习重点:中心对称性质及其应用
(二)预学成果
1.预学作业:
问题:这些图形中,哪些是中心对称图形 ,哪些是轴对称图形
(2)平面内,如果把一个图形 ,那么这个
图形叫做中心对称图形. 就是它的对称中心.两个图形中的 叫做对称点.
2.预学检测:
(1)预习作业1中的四个图案中, 是轴对称图形, 是中心对称图形, 既是中心对称图形又是轴对称图形.
(2)中心对称图形是 个图形的特征,而中心对称是指 图形间的关系.
(3)认一认:下列常见图形哪些是轴对称图形?哪些是中心对称图形?
线段a 等边三角形b 平行四边形c
长方形d 圆形e 直角三角形f
3.预学质疑:对于中心对称与中心对称图形联系与区别的预学,你有哪些疑惑?
个性补充
【导问研学】 问题一:如何应用中心对称的基本性质解决几何问题?
活动:已知:如图:四边形ABCD是平行四边形,E、F、G、H依次在各边上,且AE = CG. BF = DH,试利用“中心对称”的有关知识说明EF 与FH互相平分.
解:连结AC.BD相交于点O.
因为四边形ABCD是平行四边形,所以△AOB与 关于点O中心对称且AB 与 为对称线段又因为E、G分别在AB、CD上,且AE = CG,所以 点E、G关于点 对称.
问题二:如何应用中心对称的基本性质解决实际问题?
活动1:工厂要制作一批正六边形的地板砖,要求在地板砖上设计的图案能把正六边形六等分.请你帮助该厂至少设计三种方案.
活动2:如图:一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线(保留作图痕迹),
【导法慧学】
中心对称和轴对称都是两个图形按某种规则运动互相重合的特殊位置关系,比较它们
的定义及性质,
个性补充
【导评促学】
1.下列图形中,既是轴对称图形,又是中心对称图形的有
2.下列说法正确的是( )
A.中心对称图形不一定是轴对称图形
B.中心对称图形的对称中心不一定唯一
C.轴对称图形一定不是中心对称图形
D.轴对称图形的对称轴不一定唯一
3.已知:AC与BD互相平分于O,E、F分别在AB.CD上,且AE = CF,试利用“中心对称”的有关知识说明:点E、O、F 在同一直线上,且OE= OF
★4.如右图,正方形ABCD和正方形OEFG的边长均为4,点O是正方形ABCD的对称中心,则图中阴影部分的面积为 .
个性补充
教学反思
钟吾中学八年级(下)数学导学案
课题 中心对称与中心对称图形(2) 课型 新授 章节 9.2
时间
课时 第 课时
学习目标:
1.认识中心对称图形,理解中心对称图形的性质,会判别轴对称和中心对称;
2.会应用中心对称的性质解决问题.
学习重点:中心对称性质及其应用
(二)预学成果
1.预学作业:
问题:这些图形中,哪些是中心对称图形 ,哪些是轴对称图形
(2)平面内,如果把一个图形 ,那么这个
图形叫做中心对称图形. 就是它的对称中心.两个图形中的 叫做对称点.
2.预学检测:
(1)预习作业1中的四个图案中, 是轴对称图形, 是中心对称图形, 既是中心对称图形又是轴对称图形.
(2)中心对称图形是 个图形的特征,而中心对称是指 图形间的关系.
(3)认一认:下列常见图形哪些是轴对称图形?哪些是中心对称图形?
线段a 等边三角形b 平行四边形c
长方形d 圆形e 直角三角形f
3.预学质疑:对于中心对称与中心对称图形联系与区别的预学,你有哪些疑惑?
个性补充
中心对称图形:④③②
轴对称图形:①④
绕着某一点旋转180,如果它能与原来的图形重合 这个点 对应点
1 2
轴对称图形:a、b、d、e
中心对称图形:c、d、e
【导问研学】 问题一:如何应用中心对称的基本性质解决几何问题?
活动:已知:如图:四边形ABCD是平行四边形,E、F、G、H依次在各边上,且AE = CG. BF = DH,试利用“中心对称”的有关知识说明EG 与FH互相平分.
解:连结AC.BD相交于点O.
因为四边形ABCD是平行四边形,所以△AOB与 关于点O中心对称且AB 与 为对称线段又因为E、G分别在AB、CD上,且AE = CG,所以 点E、G关于点 对称.
问题二:如何应用中心对称的基本性质解决实际问题?
活动1:工厂要制作一批正六边形的地板砖,要求在地板砖上设计的图案能把正六边形六等分.请你帮助该厂至少设计三种方案.
活动2:如图:一个平行四边形土地ABCD,后来在其边缘挖了一个小平行四边形水塘EFGH,现准备将其分成两块,并使其满足:两块地的面积相等,分割线恰好做成水渠,便于灌溉,请你在图中画出分界线(保留作图痕迹),
【导法慧学】
中心对称和轴对称都是两个图形按某种规则运动互相重合的特殊位置关系,比较它们
的定义及性质,
个性补充
△COD CD
点O
充分放手与学生,发挥他们的想象,拓展他们的思维。
【导评促学】
1.下列图形中,既是轴对称图形,又是中心对称图形的有
2.下列说法正确的是( )
A.中心对称图形不一定是轴对称图形
B.中心对称图形的对称中心不一定唯一
C.轴对称图形一定不是中心对称图形
D.轴对称图形的对称轴不一定唯一
3.已知:AC与BD互相平分于O,E、F分别在AB.CD上,且AE = CF,试利用“中心对称”的有关知识说明:点E、O、F 在同一直线上,且OE= OF
★4.如右图,正方形ABCD和正方形OEFG的边长均为4,点O是正方形ABCD的对称中心,则图中阴影部分的面积为 .
个性补充
⑵ ⑷
A
因为AC与BD关于点O中心对称,且AC 与BD 为对称线段又因为E、F分别在AC、BD上,且AE = CF,所以 点E、F关于点O对称.
所以OE= OF
1
先独立完成,互相批阅,找出错误,教师点评。
教学反思
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
