2020_2021学年高中数学第十一章立体几何初步章末检测精英同步练 Word含解析新人教B版必修第四册
文档属性
| 名称 | 2020_2021学年高中数学第十一章立体几何初步章末检测精英同步练 Word含解析新人教B版必修第四册 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览




文档简介
第十一章
章末检测
1、一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是(
)
A.
B.
C.
D.
都不对
2、有一个圆锥与一个圆柱的底面半径相等,圆锥的母线与底面所成角为,若圆柱的外接球的表面积是圆锥的侧面积的倍,则圆柱的高是其底面半径的(???)
A.
倍
B.
倍
C.
倍
D.
倍
3、已知三棱锥中,,则该三棱锥的外接球的体积为(
)
A.
B.
C.
D.
4、一个直角梯形的两底长分别为2和5,高为4,绕其较长的底旋转一周,所得的几何体的体积为(
)
A.
B.
C.
D.
5、在长方体中,,则当该长方体的表面积最大时,异面直线与所成角的大小为(
)
A.
B.
C.
D.
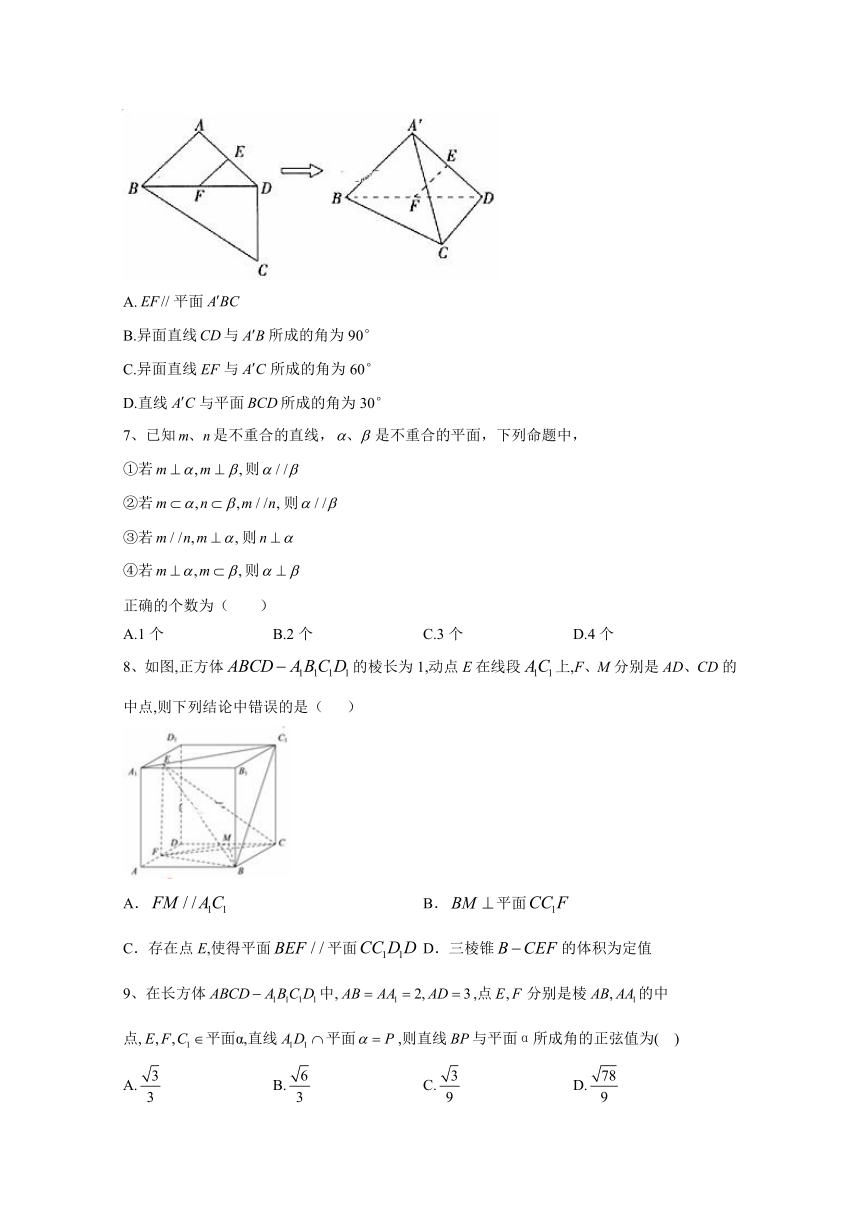
6、如图,平面四边形中,是的中点,,,,将沿对角线折起至,使平面平面,则四面体中,下列结论不正确的是(
)
A.平面
B.异面直线与所成的角为90°
C.异面直线与所成的角为60°
D.直线与平面所成的角为30°
7、已知是不重合的直线,是不重合的平面,下列命题中,
①若则
②若则
③若则
④若则
正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
8、如图,正方体的棱长为1,动点E在线段上,F、M分别是AD、CD的中点,则下列结论中错误的是(
)
A.
B.平面
C.存在点E,使得平面平面
D.三棱锥的体积为定值
9、在长方体中,,点分别是棱的中点,平面α,直线平面,则直线与平面α所成角的正弦值为(
)
A.
B.
C.
D.
10、设三棱锥的底面是正三角形,侧棱长均相等,P是棱上的点(不含端点),记直线与直线所成角为α,直线与平面所成角为β,二面角的平面角为γ,则(
)
A.
B.
C.
D.
11、已知正方体中,E为的中点,则异面直线AE与BC所成角的余弦值为________.
12、设是两条不同的直线是两个不同的平面,且直线平面直线平面给出下列说法:①””是””必要条件
②“”是””的必要条件
③””是””充要条件
④””是””的充分条件,其中所有正确说法的序号是_________.
13、如图,在长方体中,
E是(含端点)上一动点,则以下命题中,正确的序号是___________.
①
;
②与平面所成角最小为;
③三棱锥体积为定值
;
④与所成的最大角为。
14、如图,正三角形仙的中线与中位线相交于点,已知是绕旋转过程中的一个图形,现给出下列四个命题:
①?恒有平面;
②
动点在平面上的射影在线段上;
③?三棱锥的体积有最大值;
④
直线与不可能垂直.
其中正确命题的序号是__________.
?
15、如图,在多面体中,四边形,四边形均为菱形,
(1)求证:平面平面
(2)若,求二面角的余弦值
答案以及解析
1答案及解析:
答案:A
解析:∵三角形在其直观图中对应一个边长为2正三角形,
∴直观图的面积是
由斜二测画法中直观图和原图的面积的关系,
∴原三角形的面积为,
2答案及解析:
答案:A
解析:
设圆柱的高为,底面半径为,圆柱的外接球的半径为,则,
因为圆锥的母线长.所以圆锥的高为,圆锥的侧面积为,
所以,
所以,整理可得,
则,故选A.
3答案及解析:
答案:B
解析:又因为,∴是直角三角形。
取中点O,则
∴O为三棱锥外接球的球心,外接圆的半径为,
∴该三棱锥外接球的体积为,
故答案为:.
4答案及解析:
答案:C
解析:绕较长的底旋转一周得到的几何体是粮仓形,下面是底面半径为4,高为2的圆柱,上面是底面半径为4,高为3的圆锥,
所以,所得几何体的体积为.
5答案及解析:
答案:A
解析:设,根据已知,得,长方体的表面积
当且仅当时取等号,此时长方体为正方体,如图,
连接,则,则即异面直线与所成的角,易知为等边三角形,O为的中点,所以.
6答案及解析:
答案:C
解析:因为分别为和的中点,所以,则平面,故A中结论正确;
因为平面平面,交线为,且,所以平面,则,故B中结论正确;
取中点M,连接,则,所以为异面直线与所成的角,又由,,,
可知,故C中结论错误;
连接,可得,由面面垂直的性质定理可得,平面,连接,可得为直线与平面所成的角,
由,得直线与平面所成的角为30°故D中结论正确.故选C.
7答案及解析:
答案:C
解析:①因为是不重合的平面,,根据垂直于同一直线的两个平面平行,可知,故①正确;
②若时,,也满足题设条件,故②不正确;
③若,根据两条平行线中有一条垂直于平面,则另一条也垂直于这个平面,可知,故③正确;
④若,根据如果一个平面经过另一平面的垂线,那么面面垂直,可知,故④正确
故正确命题的个数为3个
故选C.
8答案及解析:
答案:C
解析:在A中,因为F、M分别是AD、CD的中点,所以,故A正确;
在B中,F,M是底面正方形边的中点,由平面几何得,又底面
,所以,,所以平面,故B正确;
在C中,BF与平面有交点,所以不存在点E,使得平面平面,故C错误.
在D中,三棱锥以面BCF为底,则高为上下底面的距离,所以三棱锥的体积为定值,故D正确.
9答案及解析:
答案:C
解析:连接并延长,交直线于点G,连接交于点P,则易知
以B为原点,,所以直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,连接,可求得,设平面α的法向量为,则,得,令,则,则,设直线与平面α所成的角为,则,故选C.
10答案及解析:
答案:B
解析:由题意,不妨设该棱锥的侧棱长与底面边长相等,闪为点P是棱以上的点(不含端点),所以直线与平面所成的角β小于直线与平面所成的角,而直线与平面所成的角小于二曲角的平角γ,所以;因为平面,所以直线直线所成的角α大于直线与平面所成的角β,即.故选B.
11答案及解析:
答案:
解析:取的中点M,连接EM,AM,
则就是异面直线AE与BC所成的角.
在中,
.
12答案及解析:
答案:①
解析:对于①由能推出,但由””不能推出””所以①正确
对于②,由””不能推出所以②不
正确.
对于③,由””不能推出””,还可能相交,所以③不
正确.
对于④,由””不能推出””,所以④不正确.
13答案及解析:
答案:①③④
解析:①由平面,且,可证.②取中点,易知为所找的线面角,为定长,则当最长时,线面角最小,当与重合时线面角最小,小于.③三棱锥顶点换为,底面大小确定,又因为,所以点到底面的距离不变,命题正确.④因为,所以异面直线所成角与相等或互补(取锐角或直角),当与重合时,此时命题正确.
14答案及解析:
答案:①②③
解析:对于命题①,由题意,知,故平面.因为平面,所以平面平面,故该命题正确;
对于命题②,由①可知正确;
对于命题③,当平面时,三棱锥的体积有最大值,故命题③正确;
对于命题④,当在平面上的射影与直线垂直时,易证与垂直,故该命题不正确.
15答案及解析:
答案:
(1)设,连接
因为四边形为菱形,所以O为的中点
因为四边形为菱形且,所以为等边三角行,所以
因为四边形为菱形,所以,因为,平面,平面,所以平面,所以平面平面
(2)如图,连接
因为,所以,又,平面,平面,,所以平面
所以平面平面
由(1)知,,所以平面,所以两两垂直
以点O为坐标原点,所在直线分别为轴建立如图所的空间直角坐标系
设,则
设平面的法向量为,则即
得,令,得平面的一个法向量为
设平面的一个法向量为,则即
令,得平面的法向量为
,由图知,二面角的平面角为钝角
所以二面角的余弦值为
解析:
PAGE
章末检测
1、一个三角形用斜二测画法画出来的直观图是边长为2的正三角形,则原三角形的面积是(
)
A.
B.
C.
D.
都不对
2、有一个圆锥与一个圆柱的底面半径相等,圆锥的母线与底面所成角为,若圆柱的外接球的表面积是圆锥的侧面积的倍,则圆柱的高是其底面半径的(???)
A.
倍
B.
倍
C.
倍
D.
倍
3、已知三棱锥中,,则该三棱锥的外接球的体积为(
)
A.
B.
C.
D.
4、一个直角梯形的两底长分别为2和5,高为4,绕其较长的底旋转一周,所得的几何体的体积为(
)
A.
B.
C.
D.
5、在长方体中,,则当该长方体的表面积最大时,异面直线与所成角的大小为(
)
A.
B.
C.
D.
6、如图,平面四边形中,是的中点,,,,将沿对角线折起至,使平面平面,则四面体中,下列结论不正确的是(
)
A.平面
B.异面直线与所成的角为90°
C.异面直线与所成的角为60°
D.直线与平面所成的角为30°
7、已知是不重合的直线,是不重合的平面,下列命题中,
①若则
②若则
③若则
④若则
正确的个数为(
)
A.1个
B.2个
C.3个
D.4个
8、如图,正方体的棱长为1,动点E在线段上,F、M分别是AD、CD的中点,则下列结论中错误的是(
)
A.
B.平面
C.存在点E,使得平面平面
D.三棱锥的体积为定值
9、在长方体中,,点分别是棱的中点,平面α,直线平面,则直线与平面α所成角的正弦值为(
)
A.
B.
C.
D.
10、设三棱锥的底面是正三角形,侧棱长均相等,P是棱上的点(不含端点),记直线与直线所成角为α,直线与平面所成角为β,二面角的平面角为γ,则(
)
A.
B.
C.
D.
11、已知正方体中,E为的中点,则异面直线AE与BC所成角的余弦值为________.
12、设是两条不同的直线是两个不同的平面,且直线平面直线平面给出下列说法:①””是””必要条件
②“”是””的必要条件
③””是””充要条件
④””是””的充分条件,其中所有正确说法的序号是_________.
13、如图,在长方体中,
E是(含端点)上一动点,则以下命题中,正确的序号是___________.
①
;
②与平面所成角最小为;
③三棱锥体积为定值
;
④与所成的最大角为。
14、如图,正三角形仙的中线与中位线相交于点,已知是绕旋转过程中的一个图形,现给出下列四个命题:
①?恒有平面;
②
动点在平面上的射影在线段上;
③?三棱锥的体积有最大值;
④
直线与不可能垂直.
其中正确命题的序号是__________.
?
15、如图,在多面体中,四边形,四边形均为菱形,
(1)求证:平面平面
(2)若,求二面角的余弦值
答案以及解析
1答案及解析:
答案:A
解析:∵三角形在其直观图中对应一个边长为2正三角形,
∴直观图的面积是
由斜二测画法中直观图和原图的面积的关系,
∴原三角形的面积为,
2答案及解析:
答案:A
解析:
设圆柱的高为,底面半径为,圆柱的外接球的半径为,则,
因为圆锥的母线长.所以圆锥的高为,圆锥的侧面积为,
所以,
所以,整理可得,
则,故选A.
3答案及解析:
答案:B
解析:又因为,∴是直角三角形。
取中点O,则
∴O为三棱锥外接球的球心,外接圆的半径为,
∴该三棱锥外接球的体积为,
故答案为:.
4答案及解析:
答案:C
解析:绕较长的底旋转一周得到的几何体是粮仓形,下面是底面半径为4,高为2的圆柱,上面是底面半径为4,高为3的圆锥,
所以,所得几何体的体积为.
5答案及解析:
答案:A
解析:设,根据已知,得,长方体的表面积
当且仅当时取等号,此时长方体为正方体,如图,
连接,则,则即异面直线与所成的角,易知为等边三角形,O为的中点,所以.
6答案及解析:
答案:C
解析:因为分别为和的中点,所以,则平面,故A中结论正确;
因为平面平面,交线为,且,所以平面,则,故B中结论正确;
取中点M,连接,则,所以为异面直线与所成的角,又由,,,
可知,故C中结论错误;
连接,可得,由面面垂直的性质定理可得,平面,连接,可得为直线与平面所成的角,
由,得直线与平面所成的角为30°故D中结论正确.故选C.
7答案及解析:
答案:C
解析:①因为是不重合的平面,,根据垂直于同一直线的两个平面平行,可知,故①正确;
②若时,,也满足题设条件,故②不正确;
③若,根据两条平行线中有一条垂直于平面,则另一条也垂直于这个平面,可知,故③正确;
④若,根据如果一个平面经过另一平面的垂线,那么面面垂直,可知,故④正确
故正确命题的个数为3个
故选C.
8答案及解析:
答案:C
解析:在A中,因为F、M分别是AD、CD的中点,所以,故A正确;
在B中,F,M是底面正方形边的中点,由平面几何得,又底面
,所以,,所以平面,故B正确;
在C中,BF与平面有交点,所以不存在点E,使得平面平面,故C错误.
在D中,三棱锥以面BCF为底,则高为上下底面的距离,所以三棱锥的体积为定值,故D正确.
9答案及解析:
答案:C
解析:连接并延长,交直线于点G,连接交于点P,则易知
以B为原点,,所以直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,连接,可求得,设平面α的法向量为,则,得,令,则,则,设直线与平面α所成的角为,则,故选C.
10答案及解析:
答案:B
解析:由题意,不妨设该棱锥的侧棱长与底面边长相等,闪为点P是棱以上的点(不含端点),所以直线与平面所成的角β小于直线与平面所成的角,而直线与平面所成的角小于二曲角的平角γ,所以;因为平面,所以直线直线所成的角α大于直线与平面所成的角β,即.故选B.
11答案及解析:
答案:
解析:取的中点M,连接EM,AM,
则就是异面直线AE与BC所成的角.
在中,
.
12答案及解析:
答案:①
解析:对于①由能推出,但由””不能推出””所以①正确
对于②,由””不能推出所以②不
正确.
对于③,由””不能推出””,还可能相交,所以③不
正确.
对于④,由””不能推出””,所以④不正确.
13答案及解析:
答案:①③④
解析:①由平面,且,可证.②取中点,易知为所找的线面角,为定长,则当最长时,线面角最小,当与重合时线面角最小,小于.③三棱锥顶点换为,底面大小确定,又因为,所以点到底面的距离不变,命题正确.④因为,所以异面直线所成角与相等或互补(取锐角或直角),当与重合时,此时命题正确.
14答案及解析:
答案:①②③
解析:对于命题①,由题意,知,故平面.因为平面,所以平面平面,故该命题正确;
对于命题②,由①可知正确;
对于命题③,当平面时,三棱锥的体积有最大值,故命题③正确;
对于命题④,当在平面上的射影与直线垂直时,易证与垂直,故该命题不正确.
15答案及解析:
答案:
(1)设,连接
因为四边形为菱形,所以O为的中点
因为四边形为菱形且,所以为等边三角行,所以
因为四边形为菱形,所以,因为,平面,平面,所以平面,所以平面平面
(2)如图,连接
因为,所以,又,平面,平面,,所以平面
所以平面平面
由(1)知,,所以平面,所以两两垂直
以点O为坐标原点,所在直线分别为轴建立如图所的空间直角坐标系
设,则
设平面的法向量为,则即
得,令,得平面的一个法向量为
设平面的一个法向量为,则即
令,得平面的法向量为
,由图知,二面角的平面角为钝角
所以二面角的余弦值为
解析:
PAGE
