人教版八年级数学上册教学设计:11.2.2 三角形的外角
文档属性
| 名称 | 人教版八年级数学上册教学设计:11.2.2 三角形的外角 |

|
|
| 格式 | zip | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览

文档简介
八年级数学上册教学设计
课题
11.2.2
三角形的外角
教学
目标
1.三角形的外角可以解决求角的度数;是四边形和圆证明角等或是找角之间的关系的基础。
2.三角形的内角和与外角和计算角的度数
3.正确找出外角;理解三角形内角和定理的推论并会运用;数学兴趣的培养。
教学
重点
三角形外角的定义。
2.由三角形内角和定理证明它的推论及外角和。
教学
难点
三角形的外角等于与它不相邻的两个内角的和
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、外角定义和外角的性质
1.如图1,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做____________.
分析:剖析三角形外角的定义,是三角形的内角的两条边,其中一条的反向延长线,与另一边组成的角。同时我们从图中又可以发现。三角形的外角与它相邻的内角是互为邻补角的。
2.如图1,△ABC中,∠A=80°,∠B=40°,∠ACD是△ABC的一个外角,则∠ACD=___°.
试猜想∠ACD与∠A,∠B的关系是____________.
3.如图2,一个三角形有___个外角.
每个顶点处有___个外角,这两个外角是_______.
4.任意一个三角形的一个外角与它不相邻的两个外角是否都有这种关系?
证明:过点C作CM∥AB,延长BC到D
.
则∠ACM=∠A,(
)
∠MCD=∠B.
(
)
所以∠ACM
+
∠MCD
=∠A+∠B.即
∠
_____=∠A+∠B.
二、外角和定理
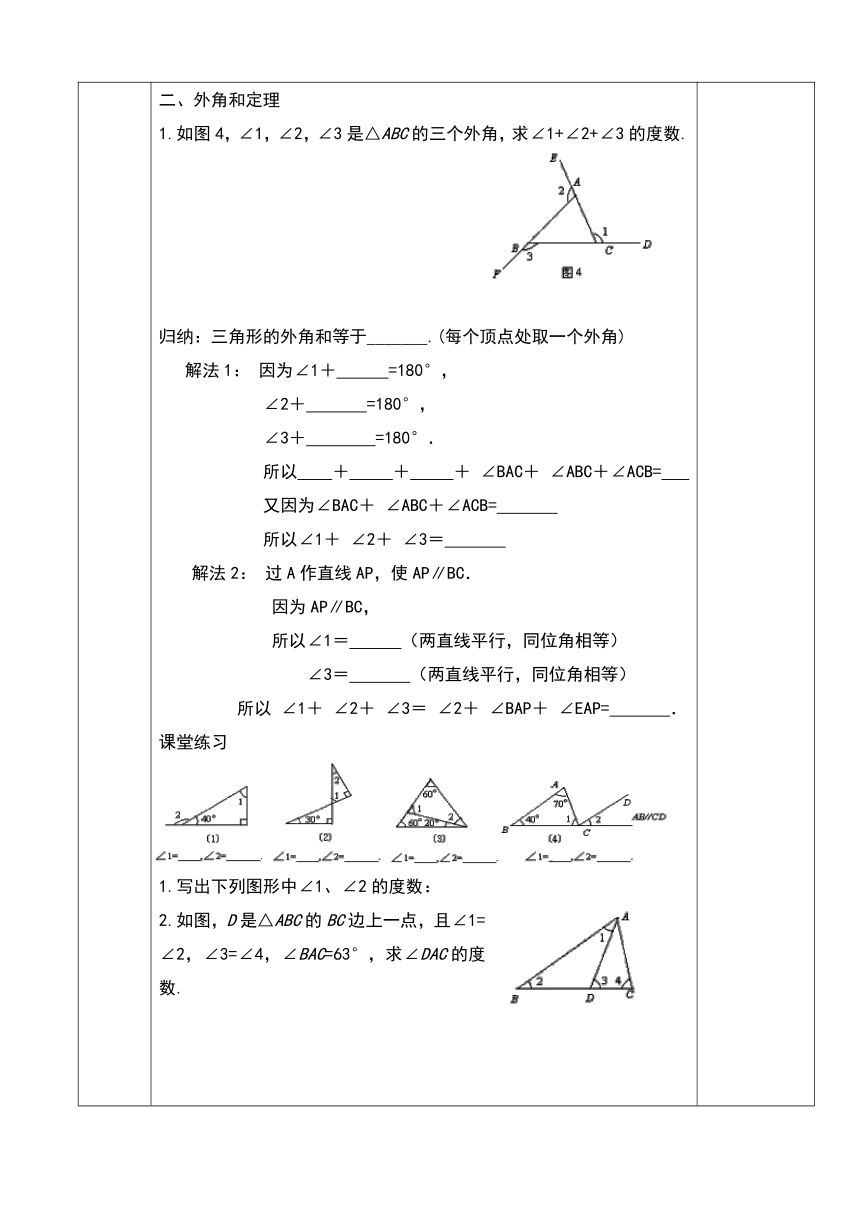
1.如图4,∠1,∠2,∠3是△ABC的三个外角,求∠1+∠2+∠3的度数.
归纳:三角形的外角和等于_______.(每个顶点处取一个外角)
解法1:
因为∠1+
=180°,
∠2+
=180°,
∠3+
=180°.
所以
+
+
+
∠BAC+
∠ABC+∠ACB=
又因为∠BAC+
∠ABC+∠ACB=
所以∠1+
∠2+
∠3=
解法2:
过A作直线AP,使AP∥BC.
因为AP∥BC,
所以∠1=
(两直线平行,同位角相等)
∠3=
(两直线平行,同位角相等)
所以
∠1+
∠2+
∠3=
∠2+
∠BAP+
∠EAP=
.
课堂练习
1.写出下列图形中∠1、∠2的度数:
2.如图,D是△ABC的BC边上一点,且∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
3.如图,D是△ABC
的BC
边上一点,∠B
=∠BAD,∠ADC
=80°,
∠BAC
=70°.求:(1)∠B
的度数;(2)∠C
的度数.
4.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数.
5.如图,在△ABC中,∠A=60°,BD、CE分别是AC、AB上的高,H是BD、CE的交点,求∠BHC的度数.
6.所示,在△ABC中,∠A=70°,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
7.所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,
求∠DAC的度数.
板
书
设
计
一、外角定义和外角的性质
二、外角和定理
教
学
反
思
课题
11.2.2
三角形的外角
教学
目标
1.三角形的外角可以解决求角的度数;是四边形和圆证明角等或是找角之间的关系的基础。
2.三角形的内角和与外角和计算角的度数
3.正确找出外角;理解三角形内角和定理的推论并会运用;数学兴趣的培养。
教学
重点
三角形外角的定义。
2.由三角形内角和定理证明它的推论及外角和。
教学
难点
三角形的外角等于与它不相邻的两个内角的和
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、外角定义和外角的性质
1.如图1,把△ABC的一边BC延长,得到∠ACD.像这样,三角形的一边与另一边的延长线组成的角,叫做____________.
分析:剖析三角形外角的定义,是三角形的内角的两条边,其中一条的反向延长线,与另一边组成的角。同时我们从图中又可以发现。三角形的外角与它相邻的内角是互为邻补角的。
2.如图1,△ABC中,∠A=80°,∠B=40°,∠ACD是△ABC的一个外角,则∠ACD=___°.
试猜想∠ACD与∠A,∠B的关系是____________.
3.如图2,一个三角形有___个外角.
每个顶点处有___个外角,这两个外角是_______.
4.任意一个三角形的一个外角与它不相邻的两个外角是否都有这种关系?
证明:过点C作CM∥AB,延长BC到D
.
则∠ACM=∠A,(
)
∠MCD=∠B.
(
)
所以∠ACM
+
∠MCD
=∠A+∠B.即
∠
_____=∠A+∠B.
二、外角和定理
1.如图4,∠1,∠2,∠3是△ABC的三个外角,求∠1+∠2+∠3的度数.
归纳:三角形的外角和等于_______.(每个顶点处取一个外角)
解法1:
因为∠1+
=180°,
∠2+
=180°,
∠3+
=180°.
所以
+
+
+
∠BAC+
∠ABC+∠ACB=
又因为∠BAC+
∠ABC+∠ACB=
所以∠1+
∠2+
∠3=
解法2:
过A作直线AP,使AP∥BC.
因为AP∥BC,
所以∠1=
(两直线平行,同位角相等)
∠3=
(两直线平行,同位角相等)
所以
∠1+
∠2+
∠3=
∠2+
∠BAP+
∠EAP=
.
课堂练习
1.写出下列图形中∠1、∠2的度数:
2.如图,D是△ABC的BC边上一点,且∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
3.如图,D是△ABC
的BC
边上一点,∠B
=∠BAD,∠ADC
=80°,
∠BAC
=70°.求:(1)∠B
的度数;(2)∠C
的度数.
4.如图3,在△ABC中,AE是角平分线,且∠B=52°,∠C=78°,求∠AEB的度数.
5.如图,在△ABC中,∠A=60°,BD、CE分别是AC、AB上的高,H是BD、CE的交点,求∠BHC的度数.
6.所示,在△ABC中,∠A=70°,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
7.所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,
求∠DAC的度数.
板
书
设
计
一、外角定义和外角的性质
二、外角和定理
教
学
反
思
