人教版八年级数学上册11.3.1多边形教学设计
文档属性
| 名称 | 人教版八年级数学上册11.3.1多边形教学设计 |
|
|
| 格式 | zip | ||
| 文件大小 | 52.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览

文档简介
八年级数学上册教学设计
课题
11.3.1多边形
教学
目标
1.多边形定义的准确理解。主要区别于三角形定义的关键条件。
2.多边形的对角线的概念及公式推导。
3.正多边形的概念
教学
重点
多边形的定义的理解;正多边形的定义理解。
教学
难点
正确判断多边形有几条对角线。一条对角线将n边形分成几个三角形。
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、多边形概念
1.定义:在同一平面内由一些线段首尾顺次相接组成封闭图形叫做多边形。边数为n时的多边形叫做n边形。
⑴多边形的内角:多边形相邻两边组成的角叫做多边形的内角。
⑵多边形的外角:多边形的边与它邻边的延长线组成的角叫做外角。
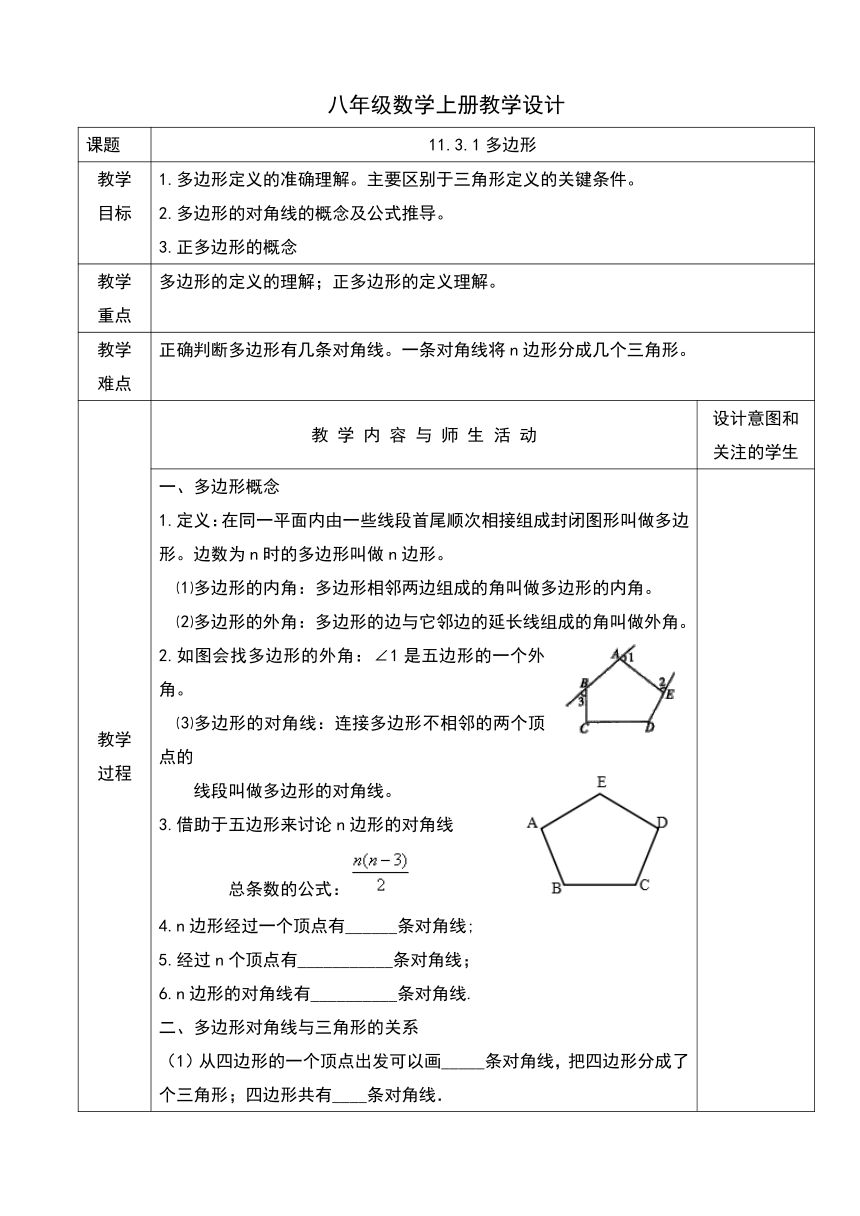
2.如图会找多边形的外角:∠1是五边形的一个外角。
⑶多边形的对角线:连接多边形不相邻的两个顶点的
线段叫做多边形的对角线。
3.借助于五边形来讨论n边形的对角线
总条数的公式:
4.n边形经过一个顶点有______条对角线;
5.经过n个顶点有___________条对角线;
6.n边形的对角线有__________条对角线.
二、多边形对角线与三角形的关系
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了
个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了
个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了
个三角形;六边形共有____条对角线.
三、正多边形的概念
1.正多边形的定义:各个角都相等
各条边都相等的多边形叫做正多边形。
注:定义中的两个条件缺一不可。
2.长方形_____正多边形。(填“是”或“不是”
)
3.菱形________正多边形。
课堂练习
1、n边形有____个内角.
2、画出下列多边形的全部对角线:
3、下图中的五边形应表示为
___________
,指出它的内角和已有的外角,并在左图中画出它所有的对角线,在右图每个顶点处各再画出一个外角.
解:如图,五边形的内角是_________________;
已有的外角是_________;它有_____条对角线.
3、下面两图哪个是凸多边形?
4、三角形_____凸多边形,五角星____凸多边形(填上“是”或“不是”).
注意:若没有特殊说明,我们在习题、作业中提到的多边形都是凸多边形.
5、下面的图形都是正多边形,请你观察图形并写出它们的名称:
6、判断:(1)等腰三角形是正多边形
。
(
)
(2)等边三角形是正多边形。
(
)
(3)平行四边形是正多边形。
(
)
(4)长方形是正多边形。
(
)
(4)菱形是正多边形。
(
)
(5)正方形是正多边形。
(
)
板
书
设
计
一、多边形概念
二、多边形对角线与三角形的关系
三、正多边形的概念
教
学
反
思
课题
11.3.1多边形
教学
目标
1.多边形定义的准确理解。主要区别于三角形定义的关键条件。
2.多边形的对角线的概念及公式推导。
3.正多边形的概念
教学
重点
多边形的定义的理解;正多边形的定义理解。
教学
难点
正确判断多边形有几条对角线。一条对角线将n边形分成几个三角形。
教学
过程
教
学
内
容
与
师
生
活
动
设计意图和
关注的学生
一、多边形概念
1.定义:在同一平面内由一些线段首尾顺次相接组成封闭图形叫做多边形。边数为n时的多边形叫做n边形。
⑴多边形的内角:多边形相邻两边组成的角叫做多边形的内角。
⑵多边形的外角:多边形的边与它邻边的延长线组成的角叫做外角。
2.如图会找多边形的外角:∠1是五边形的一个外角。
⑶多边形的对角线:连接多边形不相邻的两个顶点的
线段叫做多边形的对角线。
3.借助于五边形来讨论n边形的对角线
总条数的公式:
4.n边形经过一个顶点有______条对角线;
5.经过n个顶点有___________条对角线;
6.n边形的对角线有__________条对角线.
二、多边形对角线与三角形的关系
(1)从四边形的一个顶点出发可以画_____条对角线,把四边形分成了
个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了
个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了
个三角形;六边形共有____条对角线.
三、正多边形的概念
1.正多边形的定义:各个角都相等
各条边都相等的多边形叫做正多边形。
注:定义中的两个条件缺一不可。
2.长方形_____正多边形。(填“是”或“不是”
)
3.菱形________正多边形。
课堂练习
1、n边形有____个内角.
2、画出下列多边形的全部对角线:
3、下图中的五边形应表示为
___________
,指出它的内角和已有的外角,并在左图中画出它所有的对角线,在右图每个顶点处各再画出一个外角.
解:如图,五边形的内角是_________________;
已有的外角是_________;它有_____条对角线.
3、下面两图哪个是凸多边形?
4、三角形_____凸多边形,五角星____凸多边形(填上“是”或“不是”).
注意:若没有特殊说明,我们在习题、作业中提到的多边形都是凸多边形.
5、下面的图形都是正多边形,请你观察图形并写出它们的名称:
6、判断:(1)等腰三角形是正多边形
。
(
)
(2)等边三角形是正多边形。
(
)
(3)平行四边形是正多边形。
(
)
(4)长方形是正多边形。
(
)
(4)菱形是正多边形。
(
)
(5)正方形是正多边形。
(
)
板
书
设
计
一、多边形概念
二、多边形对角线与三角形的关系
三、正多边形的概念
教
学
反
思
