第1章全等三角形 题型专项训练-苏科版八年级数学上册期末复习(word版含答案)
文档属性
| 名称 | 第1章全等三角形 题型专项训练-苏科版八年级数学上册期末复习(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 426.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 10:49:10 | ||
图片预览



文档简介
八年级上册期末复习一:全等三角形
知识导图:
题型与方法
题型1:根据全等三角形性质计算
1.如图,△ABD≌△ACE,∠AEC=110°,则∠DAE的度数为(
).
A.
30°
B.
40°
C.
50°
D.60°
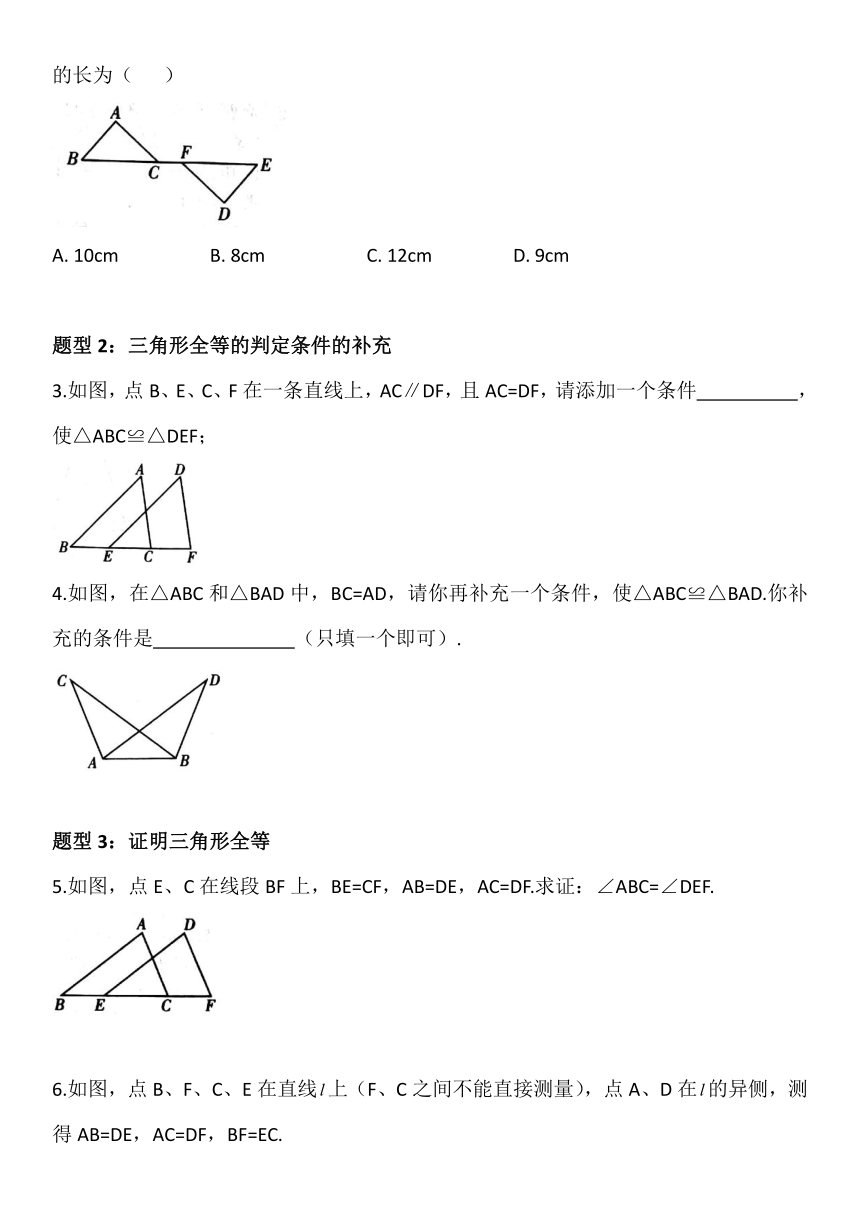
2.如图,若△ABC≌DEF,△DEF的周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC的长为(
)
A.
10cm
B.
8cm
C.
12cm
D.
9cm
题型2:三角形全等的判定条件的补充
3.如图,点B、E、C、F在一条直线上,AC∥DF,且AC=DF,请添加一个条件
,使△ABC≌△DEF;
4.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是
(只填一个即可).
题型3:证明三角形全等
5.如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.
6.如图,点B、F、C、E在直线上(F、C之间不能直接测量),点A、D在的异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
题型4:尺规作图
7.如图,在△ABC中,AB=AC,点D在△ABC的外部,∠ACD=∠B,∠ADC=90°.
(1)作图,作∠BAC的平分线AO,交BC于点O(用尺规作图,保留作图痕迹,不写作法);
(2)求证:BC=2CD.
随堂小练习
8.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应该钉在(
).
A.
A、C两点之间
B.
E、G两点之间
C.
B、F两点之间
D.G、H两点之间
9.若△ABC≌△DEF,AB=2,AC=4,且△DEF的周长为奇数,则EF的值为(
).
3
B.
4
C.
3或5
D.3或4或5
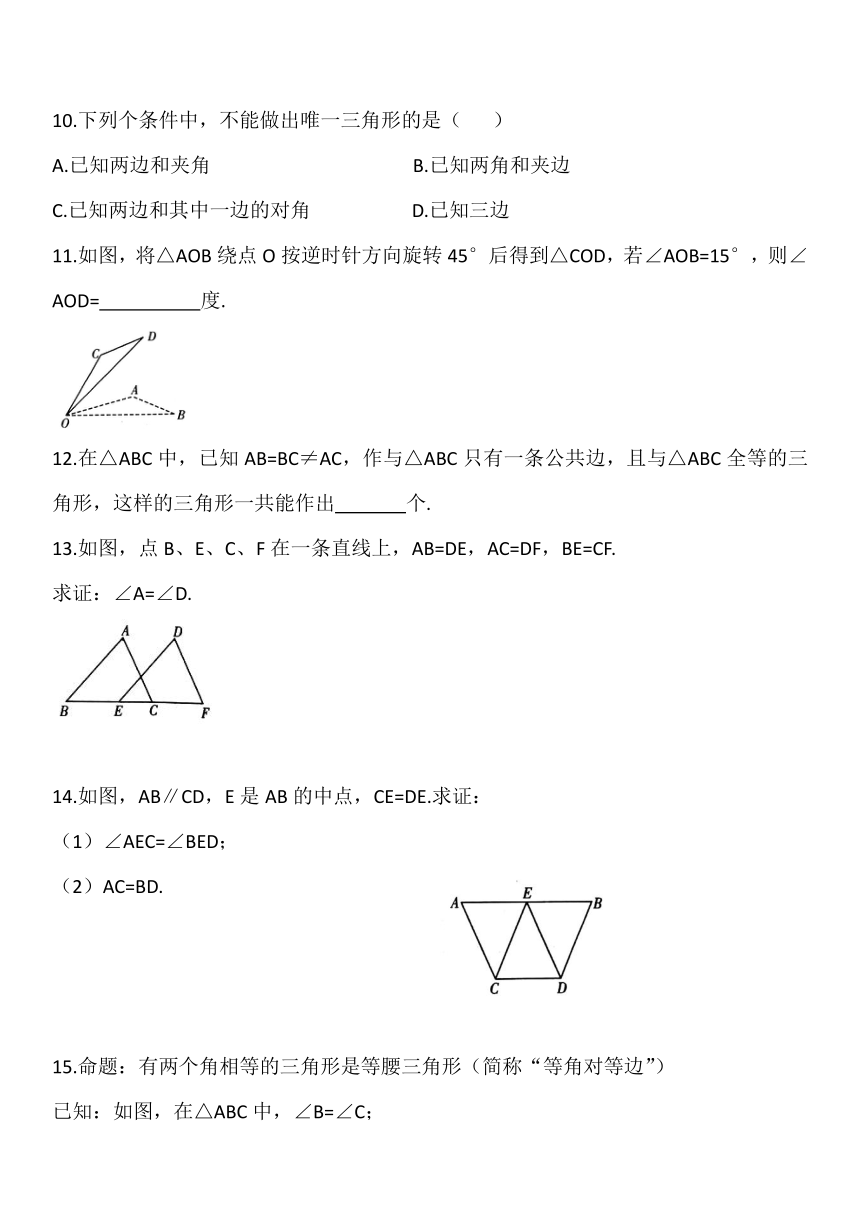
10.下列个条件中,不能做出唯一三角形的是(
)
A.已知两边和夹角
B.已知两角和夹边
C.已知两边和其中一边的对角
D.已知三边
11.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=
度.
12.在△ABC中,已知AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出
个.
13.如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D.
14.如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
15.命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”)
已知:如图,在△ABC中,∠B=∠C;
求证:AB=AC.
三位同学给出了不同的辅助线,并完成了命题的证明.小刚的方法:作∠BAC的平分线AD,可证明△ABD≌△ACD,得AB=AC;小亮的方法:作BC边上的高AD,可证明△ABD≌△ACD,得AB=AC;小莉的方法:作BC边上的中线AD.
请你写出小刚与小亮方法中△ABD≌△ACD的理由:
.
请你按照小莉的思路完成命题的证明.
提优特训:全等三角形中的辅助线的作法
类型1:倍长中线(线段)造全等
1.如图,在△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
类型2:截长补短
2.如图,AD∥BC,EA、EB分别平分∠DAB、∠CBA,CD过点E,求证:AB=AD+BC.
类型3:借助角平分线构造全等
3.如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O.
求证:OE=OD,DC+AE=AC.
类型四:旋转
4.在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
参考答案
1.B
2.A
3.答案不唯一,如∠A=∠D
4.AC=BD(或∠CBA=∠DAB)
5.∵BE=CF
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF.
6.(1)∵BF=CE,
∴BF+FC=FC+CE,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)结论:AB∥DE,AC∥DF,理由如下:
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE.
∴AB∥DE,AC∥DF.
7.(1)略.
(2)在△ABO和△ACO中,
∴△ABO≌△ACO,
∴∠AOB=∠AOC,BO=CO.
∵∠AOB+∠AOC=180°,
∴∠AOB=90°
在△ABO和△ACD中,
∴△ABO≌△ACD,
∴BO=CD,
∵OB=OC,
∴BC=2CD.
B
9.
C
10.
C
11.
30
12.
7
13.∵BE=CF,
∴BC=EF,
在△ABC和△DEF
中,
∴△ABC≌△DEF(SSS),
∴∠A=∠D
14.(1)∵AB∥CD,
∴∠AEC=∠ECD,∠BED=∠EDC.
∵CE=DE
∴△ECD是等腰三角形,
∴∠ECD=∠EDC,
∴∠AEC=∠BED.
(2)∵E是AB的中点,
∴AE=BE.
在△AEC和△BED中,
∴△AEC≌△BED(SAS).
∴AC=BD.
15.(1)AAS
(2)如图,过点D作DE⊥AB于点E,过点D作DF⊥AC于点F.
∵∠BED=∠CFD=90°,∠B=∠C,BD=CD,
∴△BDE≌△CDF(AAS),
∴BE=CF,DE=DF,
在Rt△AED和Rt△AFD中,∠AED=∠AFD=90°,
∵AD=AD,DE=DF.
∴Rt△AED≌Rt△AFD,
∴AE=AF,
∴AE+BE=AF+CF,即AB=AC.
提优特训
1.延长AE至点G,使AG=2AE,连接BG、DG.
∵AE=GE,∠AEC=∠GED,CE=DE,
∴DG=CA,∠ACB=∠EDG.
∵AC=DG,
∴∠ADC=∠CAD.
∴∠ADB=∠CAD+∠ACB=∠ADC+∠ACB=∠ADC+∠EDG=∠ADG.
又BD=AC,
∴BD=GD.
∴△ADB≌△ADG(ASA),
∴∠BAD=∠GAD,即AD平分∠BAE.
2.(截长法)在AB上取点F,使AF=AD,连接FE,
易知△ADE≌△AFE(SAS)
∴∠ADE=∠AFE.
∵AD∥BC,
∴∠ADE+∠BCE=180°.
又∠AFE+∠BFE=180°,
∴∠ECB=∠BFE,
∴△FBE≌△CBE(AAS),
∴BF=BC,
∴AB=AD+BC.
3.∵∠B=60°,
∴∠BAC+∠BCA=120°,
∵AD、CE均为角平分线,
∴∠OAC+∠OCA=60°=∠AOE=∠COD,∠AOC=120°.
在AC上截取线段AF=AE,连接OF.
又AO=AO,∠OAE=∠OAF,
∴△OAE≌△OAF(SAS),
∴OE=OF,AE=AF,∠AOF=∠AOE=60°,
∴∠COF=∠AOC-∠AOF=60°=∠COD.
又CO=CO,∠OCD=∠OCF,
∴△OCD≌△OCF(ASA),
∴OD=OF,CD=CF,
∴OE=OD,
∴DC+AE=CF+AF=AC.
4.将△ADF绕点A顺时针旋转90°至△ABG,交CB的延长线于点G,则GE=GB+BE=DF+BE=EF.
又AE=AE,AF=AG,
∴△AEF≌△AEG(SSS),
∴∠EAF=∠GAE=∠BAE+∠GAB=∠BAE+∠DAF.
又∠EAF+∠BAE+∠DAF=90°,
∴∠EAF=45°.
知识导图:
题型与方法
题型1:根据全等三角形性质计算
1.如图,△ABD≌△ACE,∠AEC=110°,则∠DAE的度数为(
).
A.
30°
B.
40°
C.
50°
D.60°
2.如图,若△ABC≌DEF,△DEF的周长是32cm,DE=9cm,EF=13cm,∠E=∠B,则AC的长为(
)
A.
10cm
B.
8cm
C.
12cm
D.
9cm
题型2:三角形全等的判定条件的补充
3.如图,点B、E、C、F在一条直线上,AC∥DF,且AC=DF,请添加一个条件
,使△ABC≌△DEF;
4.如图,在△ABC和△BAD中,BC=AD,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是
(只填一个即可).
题型3:证明三角形全等
5.如图,点E、C在线段BF上,BE=CF,AB=DE,AC=DF.求证:∠ABC=∠DEF.
6.如图,点B、F、C、E在直线上(F、C之间不能直接测量),点A、D在的异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
题型4:尺规作图
7.如图,在△ABC中,AB=AC,点D在△ABC的外部,∠ACD=∠B,∠ADC=90°.
(1)作图,作∠BAC的平分线AO,交BC于点O(用尺规作图,保留作图痕迹,不写作法);
(2)求证:BC=2CD.
随堂小练习
8.如图,工人师傅做了一个长方形窗框ABCD,E、F、G、H分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应该钉在(
).
A.
A、C两点之间
B.
E、G两点之间
C.
B、F两点之间
D.G、H两点之间
9.若△ABC≌△DEF,AB=2,AC=4,且△DEF的周长为奇数,则EF的值为(
).
3
B.
4
C.
3或5
D.3或4或5
10.下列个条件中,不能做出唯一三角形的是(
)
A.已知两边和夹角
B.已知两角和夹边
C.已知两边和其中一边的对角
D.已知三边
11.如图,将△AOB绕点O按逆时针方向旋转45°后得到△COD,若∠AOB=15°,则∠AOD=
度.
12.在△ABC中,已知AB=BC≠AC,作与△ABC只有一条公共边,且与△ABC全等的三角形,这样的三角形一共能作出
个.
13.如图,点B、E、C、F在一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D.
14.如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
15.命题:有两个角相等的三角形是等腰三角形(简称“等角对等边”)
已知:如图,在△ABC中,∠B=∠C;
求证:AB=AC.
三位同学给出了不同的辅助线,并完成了命题的证明.小刚的方法:作∠BAC的平分线AD,可证明△ABD≌△ACD,得AB=AC;小亮的方法:作BC边上的高AD,可证明△ABD≌△ACD,得AB=AC;小莉的方法:作BC边上的中线AD.
请你写出小刚与小亮方法中△ABD≌△ACD的理由:
.
请你按照小莉的思路完成命题的证明.
提优特训:全等三角形中的辅助线的作法
类型1:倍长中线(线段)造全等
1.如图,在△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.
类型2:截长补短
2.如图,AD∥BC,EA、EB分别平分∠DAB、∠CBA,CD过点E,求证:AB=AD+BC.
类型3:借助角平分线构造全等
3.如图,已知在△ABC中,∠B=60°,△ABC的角平分线AD、CE相交于点O.
求证:OE=OD,DC+AE=AC.
类型四:旋转
4.在正方形ABCD中,E为BC上的一点,F为CD上的一点,BE+DF=EF,求∠EAF的度数.
参考答案
1.B
2.A
3.答案不唯一,如∠A=∠D
4.AC=BD(或∠CBA=∠DAB)
5.∵BE=CF
∴BE+EC=CF+EC,即BC=EF,
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
∴∠ABC=∠DEF.
6.(1)∵BF=CE,
∴BF+FC=FC+CE,即BC=EF.
在△ABC和△DEF中,
∴△ABC≌△DEF(SSS)
(2)结论:AB∥DE,AC∥DF,理由如下:
∵△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE.
∴AB∥DE,AC∥DF.
7.(1)略.
(2)在△ABO和△ACO中,
∴△ABO≌△ACO,
∴∠AOB=∠AOC,BO=CO.
∵∠AOB+∠AOC=180°,
∴∠AOB=90°
在△ABO和△ACD中,
∴△ABO≌△ACD,
∴BO=CD,
∵OB=OC,
∴BC=2CD.
B
9.
C
10.
C
11.
30
12.
7
13.∵BE=CF,
∴BC=EF,
在△ABC和△DEF
中,
∴△ABC≌△DEF(SSS),
∴∠A=∠D
14.(1)∵AB∥CD,
∴∠AEC=∠ECD,∠BED=∠EDC.
∵CE=DE
∴△ECD是等腰三角形,
∴∠ECD=∠EDC,
∴∠AEC=∠BED.
(2)∵E是AB的中点,
∴AE=BE.
在△AEC和△BED中,
∴△AEC≌△BED(SAS).
∴AC=BD.
15.(1)AAS
(2)如图,过点D作DE⊥AB于点E,过点D作DF⊥AC于点F.
∵∠BED=∠CFD=90°,∠B=∠C,BD=CD,
∴△BDE≌△CDF(AAS),
∴BE=CF,DE=DF,
在Rt△AED和Rt△AFD中,∠AED=∠AFD=90°,
∵AD=AD,DE=DF.
∴Rt△AED≌Rt△AFD,
∴AE=AF,
∴AE+BE=AF+CF,即AB=AC.
提优特训
1.延长AE至点G,使AG=2AE,连接BG、DG.
∵AE=GE,∠AEC=∠GED,CE=DE,
∴DG=CA,∠ACB=∠EDG.
∵AC=DG,
∴∠ADC=∠CAD.
∴∠ADB=∠CAD+∠ACB=∠ADC+∠ACB=∠ADC+∠EDG=∠ADG.
又BD=AC,
∴BD=GD.
∴△ADB≌△ADG(ASA),
∴∠BAD=∠GAD,即AD平分∠BAE.
2.(截长法)在AB上取点F,使AF=AD,连接FE,
易知△ADE≌△AFE(SAS)
∴∠ADE=∠AFE.
∵AD∥BC,
∴∠ADE+∠BCE=180°.
又∠AFE+∠BFE=180°,
∴∠ECB=∠BFE,
∴△FBE≌△CBE(AAS),
∴BF=BC,
∴AB=AD+BC.
3.∵∠B=60°,
∴∠BAC+∠BCA=120°,
∵AD、CE均为角平分线,
∴∠OAC+∠OCA=60°=∠AOE=∠COD,∠AOC=120°.
在AC上截取线段AF=AE,连接OF.
又AO=AO,∠OAE=∠OAF,
∴△OAE≌△OAF(SAS),
∴OE=OF,AE=AF,∠AOF=∠AOE=60°,
∴∠COF=∠AOC-∠AOF=60°=∠COD.
又CO=CO,∠OCD=∠OCF,
∴△OCD≌△OCF(ASA),
∴OD=OF,CD=CF,
∴OE=OD,
∴DC+AE=CF+AF=AC.
4.将△ADF绕点A顺时针旋转90°至△ABG,交CB的延长线于点G,则GE=GB+BE=DF+BE=EF.
又AE=AE,AF=AG,
∴△AEF≌△AEG(SSS),
∴∠EAF=∠GAE=∠BAE+∠GAB=∠BAE+∠DAF.
又∠EAF+∠BAE+∠DAF=90°,
∴∠EAF=45°.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
