高中数学人教A版1.3.2 函数的奇偶性 课件(24张PPT)
文档属性
| 名称 | 高中数学人教A版1.3.2 函数的奇偶性 课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:27:55 | ||
图片预览





文档简介
毕达哥拉斯曾说:“一切平面图形中,最美的是圆形。”
那是因为圆在各个方向上都是对称的,是一种极致的美,是最完美的对称,可以这样说,大自然便是用对称来组织与生成 的。
1.3.2 函数的奇偶性
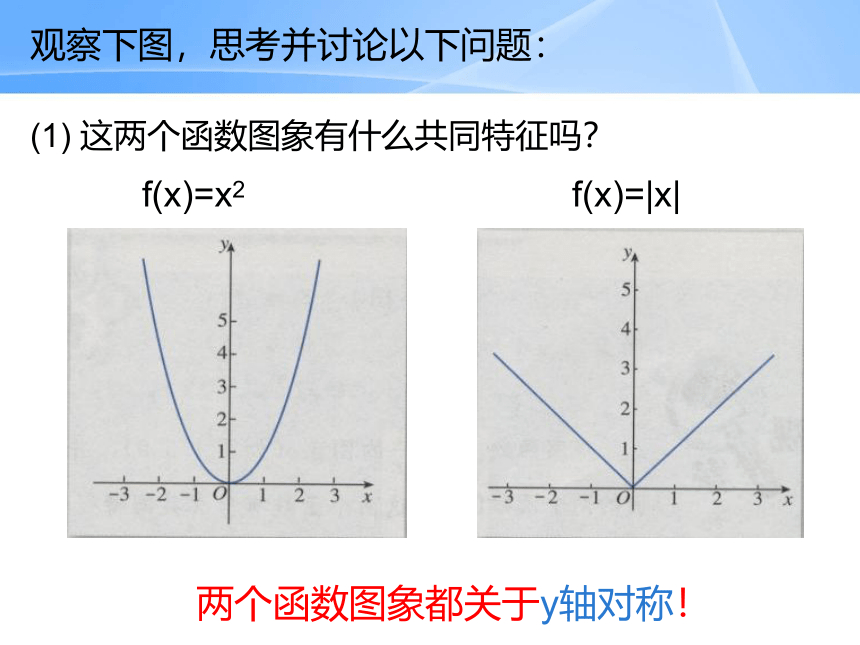
观察下图,思考并讨论以下问题:
(1) 这两个函数图象有什么共同特征吗?
f(x)=x2
f(x)=|x|
两个函数图象都关于y轴对称!
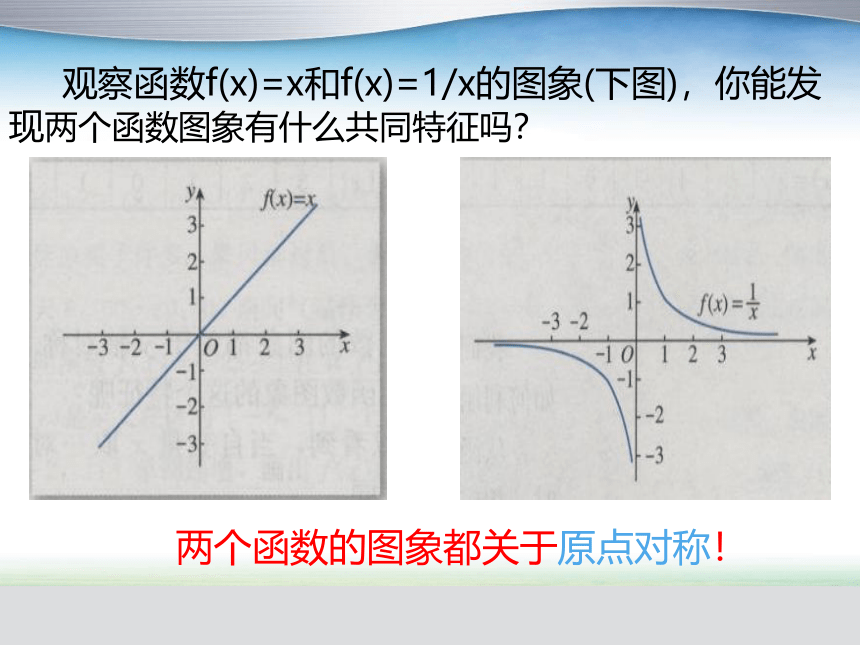
观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?
两个函数的图象都关于原点对称!
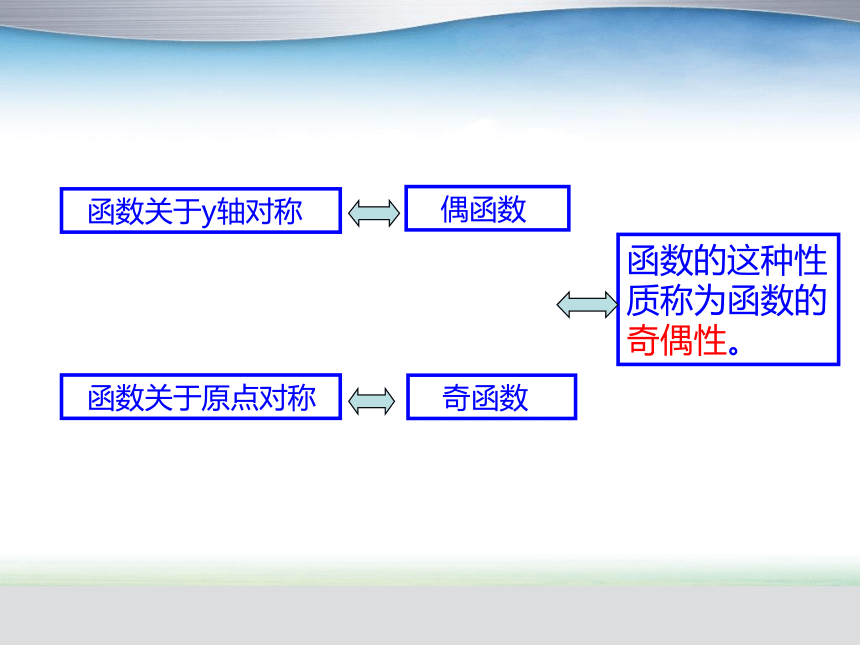
函数关于原点对称
奇函数
函数关于y轴对称
偶函数
函数的这种性质称为函数的奇偶性。
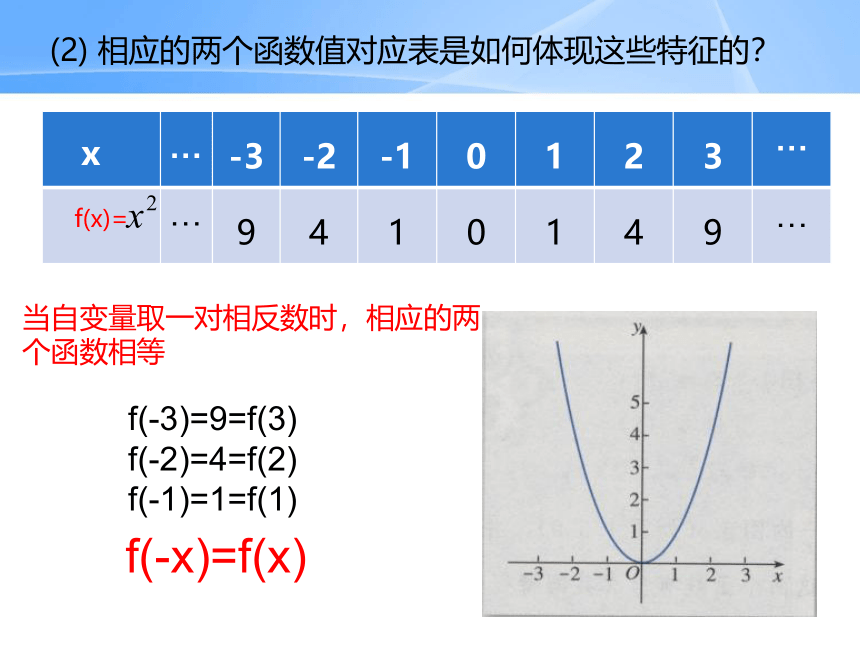
(2) 相应的两个函数值对应表是如何体现这些特征的?
x
…
-3
-2
-1
0
1
2
3
…
f(x)=
…
9
4
1
0
1
4
9
…
f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)
f(-x)=f(x)
当自变量取一对相反数时,相应的两个函数相等
偶函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
形:偶函数的图象关于y轴对称。
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x
…
-3
-2
-1
0
1
2
3
…
f(-x)=-f(x)
(2) 相应的两个函数值对应表是如何体现这些特征的?
当自变量取一对相反数时,相应的两个函数值也互为一对相反数
奇函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数.
形:奇函数的图象关于原点对称。
判断f (-x)=f (x)还是f (-x)=-f (x).
根据定义判断一个函数是奇函数还是偶函数
就是判断______?
注意:
1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
2、由函数的奇偶性定义可知,函数具有奇偶性的一个必须满足的满足条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量,x与-x必须同时在定义域内(即定义域关于原点对称).
第一步:先判断函数的定义域是否关于原点对称;
第二步:判断f (-x)=f (x)还是判断f (-x)=-f (x).
根据定义判断一个函数是奇函数还是偶函数的方法和步骤是:
函数按是否有奇偶性可分为四类:
奇函数
偶函数
既是奇函数又是偶函数
既不是奇函数又不是偶函数
小结
那是因为圆在各个方向上都是对称的,是一种极致的美,是最完美的对称,可以这样说,大自然便是用对称来组织与生成 的。
1.3.2 函数的奇偶性
观察下图,思考并讨论以下问题:
(1) 这两个函数图象有什么共同特征吗?
f(x)=x2
f(x)=|x|
两个函数图象都关于y轴对称!
观察函数f(x)=x和f(x)=1/x的图象(下图),你能发现两个函数图象有什么共同特征吗?
两个函数的图象都关于原点对称!
函数关于原点对称
奇函数
函数关于y轴对称
偶函数
函数的这种性质称为函数的奇偶性。
(2) 相应的两个函数值对应表是如何体现这些特征的?
x
…
-3
-2
-1
0
1
2
3
…
f(x)=
…
9
4
1
0
1
4
9
…
f(-3)=9=f(3) f(-2)=4=f(2) f(-1)=1=f(1)
f(-x)=f(x)
当自变量取一对相反数时,相应的两个函数相等
偶函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.
形:偶函数的图象关于y轴对称。
f(-3)=-3=-f(3) f(-2)=-2=-f(2) f(-1)=-1=-f(1)
x
…
-3
-2
-1
0
1
2
3
…
f(x)=x
…
-3
-2
-1
0
1
2
3
…
f(-x)=-f(x)
(2) 相应的两个函数值对应表是如何体现这些特征的?
当自变量取一对相反数时,相应的两个函数值也互为一对相反数
奇函数
一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数.
形:奇函数的图象关于原点对称。
判断f (-x)=f (x)还是f (-x)=-f (x).
根据定义判断一个函数是奇函数还是偶函数
就是判断______?
注意:
1、函数是奇函数或是偶函数称为函数的奇偶性,函数的奇偶性是函数的整体性质;
2、由函数的奇偶性定义可知,函数具有奇偶性的一个必须满足的满足条件是,对于定义域内的任意一个x,则-x也一定是定义域内的一个自变量,x与-x必须同时在定义域内(即定义域关于原点对称).
第一步:先判断函数的定义域是否关于原点对称;
第二步:判断f (-x)=f (x)还是判断f (-x)=-f (x).
根据定义判断一个函数是奇函数还是偶函数的方法和步骤是:
函数按是否有奇偶性可分为四类:
奇函数
偶函数
既是奇函数又是偶函数
既不是奇函数又不是偶函数
小结
