高中数学人教A版必修1第二章2.2.1对数与对数运算课件(26张PPT)
文档属性
| 名称 | 高中数学人教A版必修1第二章2.2.1对数与对数运算课件(26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:20:12 | ||
图片预览








文档简介
2.2.1对数与对数运算
教学目标
1、理解对数的概念,并能进行指数式与对数式的互化、求定义域、求值;
2、了解常用对数与自然对数的意义;
3、理解对数的性质并能用于有关对数的计算。
4、体会类比、转化的数学思想。
教学重难点
重点 :
对数的概念;对数式与指数式的相互转化。
难点 :
对数概念的理解;对数性质的理解。
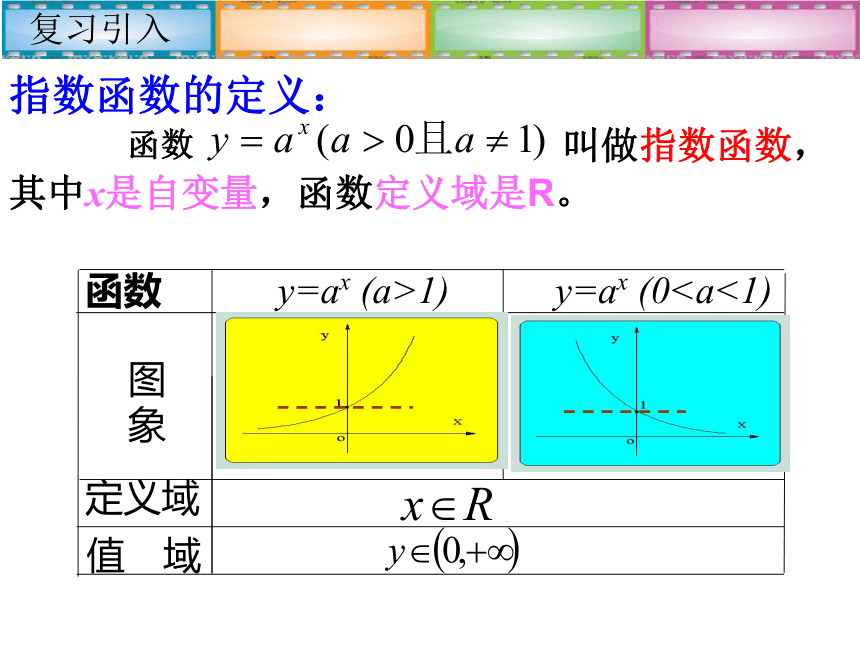
复习引入
指数函数的定义:
函数
其中x是自变量,函数定义域是R。
叫做指数函数,
函数
y=ax (a>1)
y=ax (0图
象
定义域
值 域
问题:以上式子是给出底数和指数求值,
那你能求下式的x值呢?
4
8
16
怎样求出这个
=7
探究新知
上述问题,实质就是已知 和 的值,求 .
底数
幂
指数
式子1:
式子2:
问题:观察上述两例在求值时有何共同特征?
问题:如何求指数x的值?
代数字1、2、3、4......
问题:能否像加减运算,采取“移项”的方法,用一个式子来表达?
对数
探究新知
对数的发明是17世纪数学史的重大事件。对数的创始人是苏格兰数学家纳皮尔(Napier,1550年——1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明。
纳皮尔与对数
运用对数解决实际问题(一)
例: 20世纪30年代,里克特制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的地震立氏震级M。其计算公式为M=lgA-lgA0,其中A是被测地震的最大振幅,A0是“标准地震”的振幅
碳14“半衰期”为5730年,用对数运算计算马王堆汉墓女尸出土时碳14的残余量,推算马王堆汉墓的年代。
运用对数解决实际问题(二)
探究新知
问题:什么是对数?如何读?如何写?如何用符号表示
一.对数的概念:
记作:
其中 叫做对数的底数,N 叫做真数
一般地,如果 ,那么数 叫做以 为底 的对数
对数的读法:
对数的写法:
a
N
log
对数的符号:
log
以a为底N的对数
探究新知
问题:指数式与对数式中a、x、N的名称、位置、范围分别是什么,写出名称和范围?
a
x
N
指数式
对数式
对数的底数
指数
幂值
指数的底数
真数
对数
指数对以a为底N的对数
a x = N
x = log a N
指数式
对数式
底数对底数
幂值对真数
问题:是否所有的实数都有对数?
负数和零没有对数
范围
探究新知
练习:根据对数的定义,写出x的值。
(1)
(2)
两种特殊的对数:
(1)常用对数
我们通常将以10为底的对数叫做常用对数。
为了简便,N的常用对数 ,简记作: .
(2)自然对数
在科学技术界常常使用以无理e=2.71828……
为底的对数,以e为底的对数,叫做自然对数。
为了简便,N的自然对数 ,简记为:
探究新知
例题巩固
例1:将下列指数式化为对数式,对数式化为指数式。
*
例题巩固
例2:求使式子有意义时,x的取值范围?
练习:
例3 求下列各式中x的值:
例题巩固
例题巩固
练习:课本P64页 练习第3题
(1)
(3)
(2)
(4)
=-4
=3
例题巩固
*
探究性质
问题:通过计算,你能找出下列各组式子的规律吗?
第一组
结论:
0
0
0
0
“1”的对数等于零,即
第二组
结论:
1
1
1
1
底数的对数等于“1”,即
探究性质
对数的性质:
1、“1”的对数等于零,即
2、底数的对数等于“1”,即
能力提升
例4 求下列各式x的值:
变式:
已知 ,求x的值。
能力提升
*
高考链接
1.(2016年.上海)
若log2(x+1)=3,则x= .
2.(2015年.四川)
lg0.01+log216的值是 .
3.(2014年.陕西)
已知4a=2,lgx=a,则x= .
7
2
归纳小结
1、这节课你学到了哪些知识?
2、你又学到了哪些数学思想方法?
归纳小结
一、对数的概念
二、对数式与指数式的互相转化
三、两个特殊对数
常用对数 自然对数
四、对数的基本性质
a x = N
x = log a N
a x = N
x = log a N
探究性质
问题:通过计算,你能找出下列各组式子的规律吗?
第三组
结论:
第四组
结论:
课后思考
课后作业
必做题
1、课本p74页习题2.2A组 第1、2题
2、
选做题
3、求下列各式的值。
谢谢
教学目标
1、理解对数的概念,并能进行指数式与对数式的互化、求定义域、求值;
2、了解常用对数与自然对数的意义;
3、理解对数的性质并能用于有关对数的计算。
4、体会类比、转化的数学思想。
教学重难点
重点 :
对数的概念;对数式与指数式的相互转化。
难点 :
对数概念的理解;对数性质的理解。
复习引入
指数函数的定义:
函数
其中x是自变量,函数定义域是R。
叫做指数函数,
函数
y=ax (a>1)
y=ax (0
象
定义域
值 域
问题:以上式子是给出底数和指数求值,
那你能求下式的x值呢?
4
8
16
怎样求出这个
=7
探究新知
上述问题,实质就是已知 和 的值,求 .
底数
幂
指数
式子1:
式子2:
问题:观察上述两例在求值时有何共同特征?
问题:如何求指数x的值?
代数字1、2、3、4......
问题:能否像加减运算,采取“移项”的方法,用一个式子来表达?
对数
探究新知
对数的发明是17世纪数学史的重大事件。对数的创始人是苏格兰数学家纳皮尔(Napier,1550年——1617年)。他发明了供天文计算作参考的对数,并于1614年在爱丁堡出版了《奇妙的对数定律说明书》,公布了他的发明。
纳皮尔与对数
运用对数解决实际问题(一)
例: 20世纪30年代,里克特制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大,这就是我们常说的地震立氏震级M。其计算公式为M=lgA-lgA0,其中A是被测地震的最大振幅,A0是“标准地震”的振幅
碳14“半衰期”为5730年,用对数运算计算马王堆汉墓女尸出土时碳14的残余量,推算马王堆汉墓的年代。
运用对数解决实际问题(二)
探究新知
问题:什么是对数?如何读?如何写?如何用符号表示
一.对数的概念:
记作:
其中 叫做对数的底数,N 叫做真数
一般地,如果 ,那么数 叫做以 为底 的对数
对数的读法:
对数的写法:
a
N
log
对数的符号:
log
以a为底N的对数
探究新知
问题:指数式与对数式中a、x、N的名称、位置、范围分别是什么,写出名称和范围?
a
x
N
指数式
对数式
对数的底数
指数
幂值
指数的底数
真数
对数
指数对以a为底N的对数
a x = N
x = log a N
指数式
对数式
底数对底数
幂值对真数
问题:是否所有的实数都有对数?
负数和零没有对数
范围
探究新知
练习:根据对数的定义,写出x的值。
(1)
(2)
两种特殊的对数:
(1)常用对数
我们通常将以10为底的对数叫做常用对数。
为了简便,N的常用对数 ,简记作: .
(2)自然对数
在科学技术界常常使用以无理e=2.71828……
为底的对数,以e为底的对数,叫做自然对数。
为了简便,N的自然对数 ,简记为:
探究新知
例题巩固
例1:将下列指数式化为对数式,对数式化为指数式。
*
例题巩固
例2:求使式子有意义时,x的取值范围?
练习:
例3 求下列各式中x的值:
例题巩固
例题巩固
练习:课本P64页 练习第3题
(1)
(3)
(2)
(4)
=-4
=3
例题巩固
*
探究性质
问题:通过计算,你能找出下列各组式子的规律吗?
第一组
结论:
0
0
0
0
“1”的对数等于零,即
第二组
结论:
1
1
1
1
底数的对数等于“1”,即
探究性质
对数的性质:
1、“1”的对数等于零,即
2、底数的对数等于“1”,即
能力提升
例4 求下列各式x的值:
变式:
已知 ,求x的值。
能力提升
*
高考链接
1.(2016年.上海)
若log2(x+1)=3,则x= .
2.(2015年.四川)
lg0.01+log216的值是 .
3.(2014年.陕西)
已知4a=2,lgx=a,则x= .
7
2
归纳小结
1、这节课你学到了哪些知识?
2、你又学到了哪些数学思想方法?
归纳小结
一、对数的概念
二、对数式与指数式的互相转化
三、两个特殊对数
常用对数 自然对数
四、对数的基本性质
a x = N
x = log a N
a x = N
x = log a N
探究性质
问题:通过计算,你能找出下列各组式子的规律吗?
第三组
结论:
第四组
结论:
课后思考
课后作业
必做题
1、课本p74页习题2.2A组 第1、2题
2、
选做题
3、求下列各式的值。
谢谢
