高中数学人教A版必修2第三章3.1.1倾斜角与斜率课件(45张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第三章3.1.1倾斜角与斜率课件(45张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 382.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:28:57 | ||
图片预览










文档简介
3.1 直线的倾斜 角与斜率
3.1.1 倾斜角与斜率
1、理解斜率的概念,掌握直线斜率的定义公式,会求已知直线的斜率.
2、能用增量比的概念解析直线的斜率为正?为负?为0以及斜率不存在的各种情况时直线的特点.
3、理解直线的倾斜角的概念,并了解直线的倾斜角与直线斜率之间的关系.
4、知道直线的斜率及倾斜角是与我们日常生活密切相关的,并能用它们解释生活中的某些现象.
教学目标:
问题提出:
1.在平面直角坐标系中,一次函数 y=kx+b的图象是什么?其中k,b的几何意义如何?
2.在平面直角坐标系中,经过一点P可以作无数条直线,如何区别这些直线的不同位置?
倾斜角与斜率
知识探究(一):直线的倾斜角
x
y
o
P
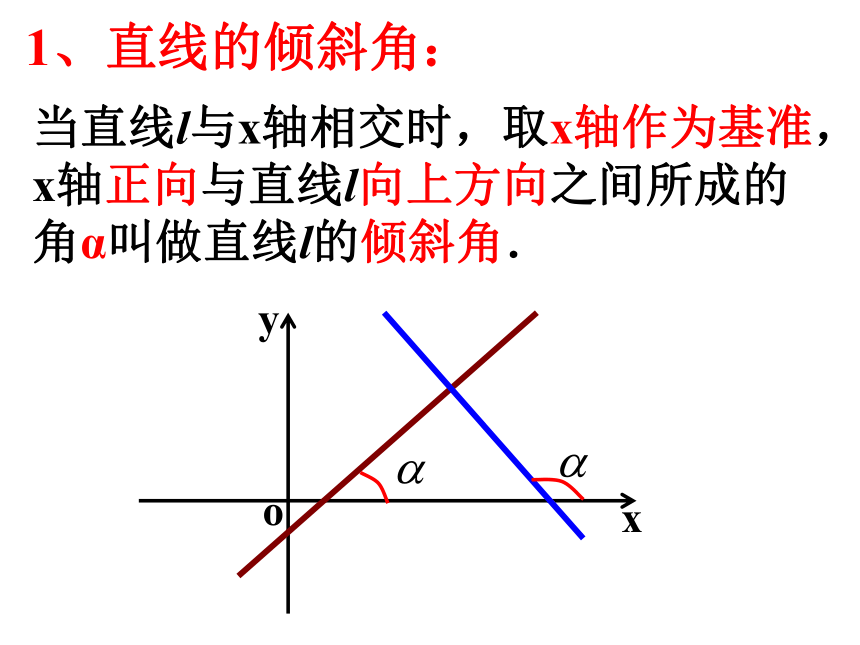
当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
x
y
o
1、直线的倾斜角:
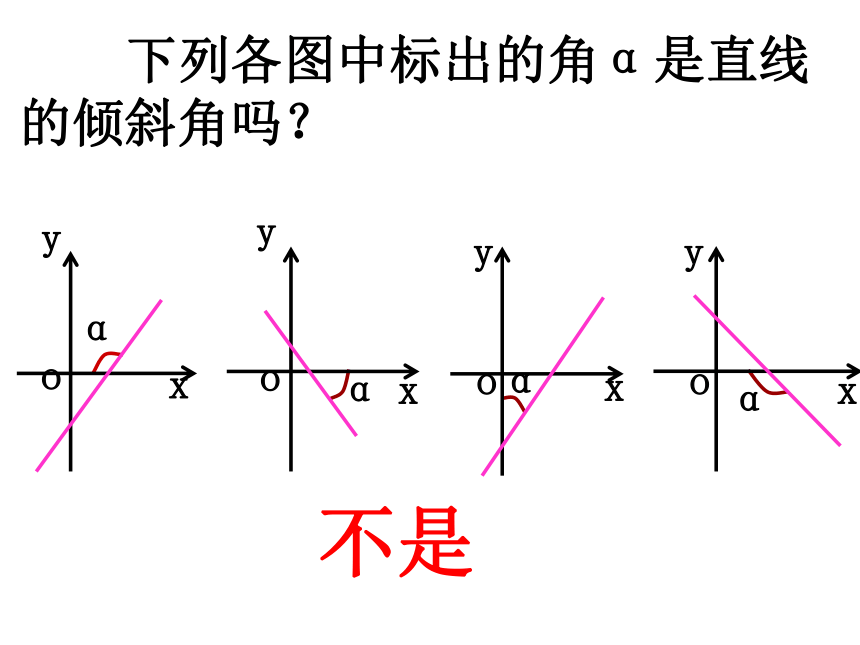
下列各图中标出的角α是直线的倾斜角吗?
x
o
y
α
x
o
y
α
x
o
y
α
o
α
x
y
不是
下图中直线l1,l2,l3的倾斜角大致是一个什么范围内的角?
x
y
o
l1
l2
l3
锐角、直角、钝角
什么是直线的倾斜角?如何理解?
1、直线倾斜角的定义可理解为:
当直线与x轴相交时,x轴绕交点按逆时针方向旋转与直线重合时所成的最小正角为直线的倾斜角,当直线与x轴平行时,规定直线的倾斜角为0°.
2、清楚定义中的三个条件:
(1)直线向上方向; (2)x轴正向;(3)0°≤α<180°.
3、任何一条直线都有唯一的倾斜角.
4、确定一条直线,必须具备两个条件:
(1)定点;
(2)倾斜角,二者缺一不可.
问: 任何一条直线都有倾斜角吗?
直线的倾斜角的取值范围:
0°≤α<180°
有
初中学过的“坡度(比)”是什么含义?它能否表示直线的倾斜程度?它与这条直线的倾斜角之间有什么关系?
前进量
升高量
α
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k表示,即k=tanα,那么任何一条直线都有斜率吗?
倾斜角是900的直线(与x轴垂直的直线)没有斜率.
2、直线的斜率:
思考2:当α是锐角时,有
tan(1800-α)=-tanα. 那么当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少?
思考1:当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少?
思考3:斜率相等的直线其倾斜角相等吗?斜率大的直线其倾斜角也大吗?
问:倾斜角为锐角、钝角的直线的斜率的取值范围分别是什么?一般地,直线的斜率的取值范围是什么?
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为00时,k=0.
倾斜角是900时没有斜率.
相等
不一定
知识探究(三):直线的斜率公式
思考1:在直角坐标系中,经过两点 A(2,4)、B(-1,3)的直线有几条?直线AB的斜率是多少?
α
C
α
x
y
o
A
B
(2,4)
(-1,3)
思考2:一般地,已知直线上的两点
P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?
x
y
o
α
P1
P2
Q
θ
x
y
o
α
P1
P2
Q
α
(x1,y1)
两点连线的斜率公式
思考3:当直线P1P2平行于x轴或与x轴重合时,上述公式还适用吗?为什么?
思考4:当直线P1P2平行于y轴或与y轴重合时,上述公式还适用吗?为什么?
适用
不适用
思考5:经过点A(a,b)、B(m,n)(a≠m)的直线的斜率是什么?
思考6:对于三个不同的点A,B,C,若 ,则这三点的位置关系如何?
三点共线
什么是直线的斜率?如何理解?
1、定义见课本P83;
2、对直线斜率的理解:
(1)由k=tanα知,当α=0°时,k=0;
当0°<α<90°时,k>0;
当α=90°时,k不存在;
当90°<α<180°时,k<0.
(2)任何一条直线的倾斜角都存在;当α=90°,斜率不存在.但直线存在,它与x轴垂直.
3、什么是直线的斜率公式?如何理解?
直线l经过点P1(x1,y1)?P2(x2,y2).
由公式k= (x2≠x1)知
(1)当x1=x2时,斜率k不存在,此时,直线l垂直x轴;
(2)当y1=y2时,k=0,此时,l平行x轴(或与x轴重合);
(3)当 时,斜率存在且
由表达式知交换点 与 公式不变,
例1 如下图,已知A(3,2),B(-4,1),
C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是纯角.
O
x
y
A
C
B
例题分析:
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
例题分析:
O
x
y
A3
A1
A2
A4
直线的倾斜角与斜率
在平面直角坐标系中,当直线l与x轴相交时,我们取x轴作为基准, x轴正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角。
当直线l和x轴平行或重合时,我们规定直线的倾斜角为00.
倾斜角不是900的直线,它的倾斜角的正切叫做这条直线的斜率,常用k来表示.
k>0,则倾斜角是锐角;k<0,则倾斜角是钝角.
小结:
小结:
斜率公式:
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是 或1800
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
练习:
F
F
F
F
T
T
练习:
l1
l2
l3
D
(3)如图,直线l1的倾斜角α1=300,
直线l1⊥l2,求l1、l2的斜率.
练习:
例1、下列叙述中不正确的是( )
A.若直线的斜率存在,则必有倾斜角与之对应;
B.每一条直线都对应唯一的倾斜角;
C.与坐标轴垂直的直线的倾斜角为0°或90°;
D.若直线的倾斜角为α,则直线的斜率为k=tanα.
题型一 斜率?倾斜角的概念
解析:由于每条直线都有唯一的倾斜角.垂直x轴的倾斜角
为90°,垂直y轴的倾斜角为0°.当倾斜角为90°时,其斜率
tanα不存在,故应选D.
D
误区警示:正确理解倾斜角?斜率的概念及它们之间的关系.
变式训练1:经过下列两点的直线的斜率是否存在?如果存在求其斜率.
(1)(-1,1)?(3,2); (2)(1,-2),(5,-2);
(3)(3,4),(2,5); (4)(2,0),(2, ).
例2、经过两点A(m2+2,m2-3),B(3-m-m2,2m)的直线l的倾斜角为135°,求m的值.
题型二 斜率公式的应用
变式训练2:当且仅当m为何值时,经过两点
A(m,2),B(-m,2m-1)的直线的倾斜角为60°?
解:连结PA?PB,kPA=-1,kPB=1,由已知l
与线段AB总有公共点,∴k∈[-1,1].
相应倾斜角α的范围是0°≤α≤45°
或135°≤α<180°.
误区警示:由斜率的范围来确定倾斜角α的范围一定要结合图形,观察直线l的运动范围.
题型三 斜率与倾斜角的关系
例3、过点P(0,-1)作直线l,若直线l与连结A(1,-2),B(2,1)的
线段总有公共点,求直线l的倾斜角α与斜率k的取值范围.
分析:作出图示,连结PA?PB,由
的变化来找倾斜角
α的范围.
解:设倾斜角为α,则k=tanα.
又0≤k<1
∴0≤tanα<1 又0°≤α<180°,∴0°≤α<45°.
变式训练3:如果直线的斜率k的取值范围是
0≤k<1,求它的倾斜角的取值范围.
例4、如图所示,已知点A(-2,3),B(3,2),P(0,-2),过点P的直线l与线段AB有公共点,求直线l的斜率k的变化范围.
易错探究
错因分析:对直线的斜率与倾斜角之间的变化关系理解不准确.直线l是一组绕点P转动而形成的直线,点A和B是它的极端位置,当l从PB位置逆时转到PA时,倾斜角从锐角变化到钝角,其斜率从正数kPB到+∞,又从-∞到一个负数kPA.
2.如下图有三条直线l1,l2,l3,倾斜角分别为α1,α2,α3,则下列关系正确的是( )
基础强化:
1.直线l经过原点和点(-1,-1),则它的斜率是( )
A.1 B.-1 C.-1或1 D.以上都不对
A
D
解析:MN⊥x轴,∴倾斜角为90°.
4.直线l经过原点和(1,-1),则它的倾斜角是( )
A.45° B.135°
C.45°或135° D.-45°
解析:k=tanα=-1,又0°≤α<180°,
∴α=135°.
3.已知M(a,b),N(a,c)(b≠c),则直线MN的
倾斜角是( )
A.不存在 B.45° C.135° D.90°
D
B
5.斜率为2的直线经过点(3,5),(a,7),(-1,b)三点,
则a,b的值是( )
A.a=4,b=0 B.a=-4,b=-3
C.a=4,b=-3 D.a=-4,b=3
C
6.已知点P(3,m)在过M(2,-1),N(-3,4)的直线上,
则m=________.
-2
7.已知点P(3,2),点Q在x轴上,若直线PQ的倾斜角为150°,
则点Q的坐标为________.
8.已知A(0,1),B(1,0),C(3,2),D(2,3),求证:四边形ABCD为
平行四边形.
解:由于AD∥BC,可知AD与BC所在直线的倾斜角都为60°,其斜率都为tan60°= .
又AB∥CD,且AB与x轴重合,
从而可知
AB与CD的倾斜角都为0°,
其斜率都为tan0°=0.
由于AC和BD是菱形的对角线,则αAC=30°,αBD=120°,其斜率分别为kAC=tan30°= ,kBD=tan120°= .
能力提升:
9.如下图,菱形ABCD中,∠BAD=60°,求菱形各边和两条对角线所在直线的倾斜角与斜率.
解:当-1≤k<0时,即-1≤tanα<0,
且0°≤α<180°,∴135°≤α<180°;
当k≥0时,即tanα≥0,
又∵0°≤α<180°,∴0°≤α<90°.
综上知,直线l的倾斜角的取值范围是[0°,90°)∪[135°,180°).
10.已知直线l的斜率k≥-1,求其倾斜角α的
取值范围.
11.若三点A(2,2),B(a,0),C(0,b),(ab≠0)共线,则 的值等于________.
12.已知a>0,若平面内三点A(1,a),B(2,a2),C(3,a3)共线,则a=________.
课堂小结:
1. 倾斜角、斜率的概念;
2. 斜率的计算公式.
作业:
P86练习:1、2、3、4.
P89习题3.1 A组:1、2、3、4、5.
P90习题3.1 B组:1、5、6
3.1.1 倾斜角与斜率
1、理解斜率的概念,掌握直线斜率的定义公式,会求已知直线的斜率.
2、能用增量比的概念解析直线的斜率为正?为负?为0以及斜率不存在的各种情况时直线的特点.
3、理解直线的倾斜角的概念,并了解直线的倾斜角与直线斜率之间的关系.
4、知道直线的斜率及倾斜角是与我们日常生活密切相关的,并能用它们解释生活中的某些现象.
教学目标:
问题提出:
1.在平面直角坐标系中,一次函数 y=kx+b的图象是什么?其中k,b的几何意义如何?
2.在平面直角坐标系中,经过一点P可以作无数条直线,如何区别这些直线的不同位置?
倾斜角与斜率
知识探究(一):直线的倾斜角
x
y
o
P
当直线l与x轴相交时,取x轴作为基准,x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.
x
y
o
1、直线的倾斜角:
下列各图中标出的角α是直线的倾斜角吗?
x
o
y
α
x
o
y
α
x
o
y
α
o
α
x
y
不是
下图中直线l1,l2,l3的倾斜角大致是一个什么范围内的角?
x
y
o
l1
l2
l3
锐角、直角、钝角
什么是直线的倾斜角?如何理解?
1、直线倾斜角的定义可理解为:
当直线与x轴相交时,x轴绕交点按逆时针方向旋转与直线重合时所成的最小正角为直线的倾斜角,当直线与x轴平行时,规定直线的倾斜角为0°.
2、清楚定义中的三个条件:
(1)直线向上方向; (2)x轴正向;(3)0°≤α<180°.
3、任何一条直线都有唯一的倾斜角.
4、确定一条直线,必须具备两个条件:
(1)定点;
(2)倾斜角,二者缺一不可.
问: 任何一条直线都有倾斜角吗?
直线的倾斜角的取值范围:
0°≤α<180°
有
初中学过的“坡度(比)”是什么含义?它能否表示直线的倾斜程度?它与这条直线的倾斜角之间有什么关系?
前进量
升高量
α
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.常用小写字母k表示,即k=tanα,那么任何一条直线都有斜率吗?
倾斜角是900的直线(与x轴垂直的直线)没有斜率.
2、直线的斜率:
思考2:当α是锐角时,有
tan(1800-α)=-tanα. 那么当倾斜角α=1200,1350,1500时,这条直线的斜率分别等于多少?
思考1:当倾斜角α=00,300,450,600时,这条直线的斜率分别等于多少?
思考3:斜率相等的直线其倾斜角相等吗?斜率大的直线其倾斜角也大吗?
问:倾斜角为锐角、钝角的直线的斜率的取值范围分别是什么?一般地,直线的斜率的取值范围是什么?
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为00时,k=0.
倾斜角是900时没有斜率.
相等
不一定
知识探究(三):直线的斜率公式
思考1:在直角坐标系中,经过两点 A(2,4)、B(-1,3)的直线有几条?直线AB的斜率是多少?
α
C
α
x
y
o
A
B
(2,4)
(-1,3)
思考2:一般地,已知直线上的两点
P1(x1,y1),P2(x2,y2),且直线P1P2与x轴不垂直,即x1≠x2,直线P1P2的斜率是什么?
x
y
o
α
P1
P2
Q
θ
x
y
o
α
P1
P2
Q
α
(x1,y1)
两点连线的斜率公式
思考3:当直线P1P2平行于x轴或与x轴重合时,上述公式还适用吗?为什么?
思考4:当直线P1P2平行于y轴或与y轴重合时,上述公式还适用吗?为什么?
适用
不适用
思考5:经过点A(a,b)、B(m,n)(a≠m)的直线的斜率是什么?
思考6:对于三个不同的点A,B,C,若 ,则这三点的位置关系如何?
三点共线
什么是直线的斜率?如何理解?
1、定义见课本P83;
2、对直线斜率的理解:
(1)由k=tanα知,当α=0°时,k=0;
当0°<α<90°时,k>0;
当α=90°时,k不存在;
当90°<α<180°时,k<0.
(2)任何一条直线的倾斜角都存在;当α=90°,斜率不存在.但直线存在,它与x轴垂直.
3、什么是直线的斜率公式?如何理解?
直线l经过点P1(x1,y1)?P2(x2,y2).
由公式k= (x2≠x1)知
(1)当x1=x2时,斜率k不存在,此时,直线l垂直x轴;
(2)当y1=y2时,k=0,此时,l平行x轴(或与x轴重合);
(3)当 时,斜率存在且
由表达式知交换点 与 公式不变,
例1 如下图,已知A(3,2),B(-4,1),
C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是纯角.
O
x
y
A
C
B
例题分析:
例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。
例题分析:
O
x
y
A3
A1
A2
A4
直线的倾斜角与斜率
在平面直角坐标系中,当直线l与x轴相交时,我们取x轴作为基准, x轴正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角。
当直线l和x轴平行或重合时,我们规定直线的倾斜角为00.
倾斜角不是900的直线,它的倾斜角的正切叫做这条直线的斜率,常用k来表示.
k>0,则倾斜角是锐角;k<0,则倾斜角是钝角.
小结:
小结:
斜率公式:
公式的特点:
(1)与两点的顺序无关;
(2) 公式表明,直线对于x轴的倾斜度,可以通过直线上任意两点的坐标来表示,而不需要求出直线的倾斜角;
(3)当x1=x2时,公式不适用,此时直线与x轴垂直,α=900
下列哪些说法是正确的( )
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
C 、平行于x轴的直线的倾斜角是 或1800
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
练习:
F
F
F
F
T
T
练习:
l1
l2
l3
D
(3)如图,直线l1的倾斜角α1=300,
直线l1⊥l2,求l1、l2的斜率.
练习:
例1、下列叙述中不正确的是( )
A.若直线的斜率存在,则必有倾斜角与之对应;
B.每一条直线都对应唯一的倾斜角;
C.与坐标轴垂直的直线的倾斜角为0°或90°;
D.若直线的倾斜角为α,则直线的斜率为k=tanα.
题型一 斜率?倾斜角的概念
解析:由于每条直线都有唯一的倾斜角.垂直x轴的倾斜角
为90°,垂直y轴的倾斜角为0°.当倾斜角为90°时,其斜率
tanα不存在,故应选D.
D
误区警示:正确理解倾斜角?斜率的概念及它们之间的关系.
变式训练1:经过下列两点的直线的斜率是否存在?如果存在求其斜率.
(1)(-1,1)?(3,2); (2)(1,-2),(5,-2);
(3)(3,4),(2,5); (4)(2,0),(2, ).
例2、经过两点A(m2+2,m2-3),B(3-m-m2,2m)的直线l的倾斜角为135°,求m的值.
题型二 斜率公式的应用
变式训练2:当且仅当m为何值时,经过两点
A(m,2),B(-m,2m-1)的直线的倾斜角为60°?
解:连结PA?PB,kPA=-1,kPB=1,由已知l
与线段AB总有公共点,∴k∈[-1,1].
相应倾斜角α的范围是0°≤α≤45°
或135°≤α<180°.
误区警示:由斜率的范围来确定倾斜角α的范围一定要结合图形,观察直线l的运动范围.
题型三 斜率与倾斜角的关系
例3、过点P(0,-1)作直线l,若直线l与连结A(1,-2),B(2,1)的
线段总有公共点,求直线l的倾斜角α与斜率k的取值范围.
分析:作出图示,连结PA?PB,由
的变化来找倾斜角
α的范围.
解:设倾斜角为α,则k=tanα.
又0≤k<1
∴0≤tanα<1 又0°≤α<180°,∴0°≤α<45°.
变式训练3:如果直线的斜率k的取值范围是
0≤k<1,求它的倾斜角的取值范围.
例4、如图所示,已知点A(-2,3),B(3,2),P(0,-2),过点P的直线l与线段AB有公共点,求直线l的斜率k的变化范围.
易错探究
错因分析:对直线的斜率与倾斜角之间的变化关系理解不准确.直线l是一组绕点P转动而形成的直线,点A和B是它的极端位置,当l从PB位置逆时转到PA时,倾斜角从锐角变化到钝角,其斜率从正数kPB到+∞,又从-∞到一个负数kPA.
2.如下图有三条直线l1,l2,l3,倾斜角分别为α1,α2,α3,则下列关系正确的是( )
基础强化:
1.直线l经过原点和点(-1,-1),则它的斜率是( )
A.1 B.-1 C.-1或1 D.以上都不对
A
D
解析:MN⊥x轴,∴倾斜角为90°.
4.直线l经过原点和(1,-1),则它的倾斜角是( )
A.45° B.135°
C.45°或135° D.-45°
解析:k=tanα=-1,又0°≤α<180°,
∴α=135°.
3.已知M(a,b),N(a,c)(b≠c),则直线MN的
倾斜角是( )
A.不存在 B.45° C.135° D.90°
D
B
5.斜率为2的直线经过点(3,5),(a,7),(-1,b)三点,
则a,b的值是( )
A.a=4,b=0 B.a=-4,b=-3
C.a=4,b=-3 D.a=-4,b=3
C
6.已知点P(3,m)在过M(2,-1),N(-3,4)的直线上,
则m=________.
-2
7.已知点P(3,2),点Q在x轴上,若直线PQ的倾斜角为150°,
则点Q的坐标为________.
8.已知A(0,1),B(1,0),C(3,2),D(2,3),求证:四边形ABCD为
平行四边形.
解:由于AD∥BC,可知AD与BC所在直线的倾斜角都为60°,其斜率都为tan60°= .
又AB∥CD,且AB与x轴重合,
从而可知
AB与CD的倾斜角都为0°,
其斜率都为tan0°=0.
由于AC和BD是菱形的对角线,则αAC=30°,αBD=120°,其斜率分别为kAC=tan30°= ,kBD=tan120°= .
能力提升:
9.如下图,菱形ABCD中,∠BAD=60°,求菱形各边和两条对角线所在直线的倾斜角与斜率.
解:当-1≤k<0时,即-1≤tanα<0,
且0°≤α<180°,∴135°≤α<180°;
当k≥0时,即tanα≥0,
又∵0°≤α<180°,∴0°≤α<90°.
综上知,直线l的倾斜角的取值范围是[0°,90°)∪[135°,180°).
10.已知直线l的斜率k≥-1,求其倾斜角α的
取值范围.
11.若三点A(2,2),B(a,0),C(0,b),(ab≠0)共线,则 的值等于________.
12.已知a>0,若平面内三点A(1,a),B(2,a2),C(3,a3)共线,则a=________.
课堂小结:
1. 倾斜角、斜率的概念;
2. 斜率的计算公式.
作业:
P86练习:1、2、3、4.
P89习题3.1 A组:1、2、3、4、5.
P90习题3.1 B组:1、5、6
