高中数学人教A版必修2第三章3.1.2两条直线平行与垂直的判定课件(18张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第三章3.1.2两条直线平行与垂直的判定课件(18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 162.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览




文档简介
3.1直线的倾斜角与斜率
3.1.2 两条直线平行与垂直的判定
问题提出:
1.直线的倾斜角和斜率的含义分别是什么?
2.经过两点的直线的斜率公式是什么?
直线的倾斜程度
相对于x轴的倾斜程度
两条直线平行与垂直的判定
为了在平面直角坐标系内表示直线的倾斜程度,我们引入了直线倾斜角的概念,进而又引入了直线的斜率——表示直线相对于x轴的倾斜程度,并导出了计算斜率的公式,即把几何问题转化为代数问题.那么,我们能否通过直线的斜率,来判断两条直线的位置关系呢?
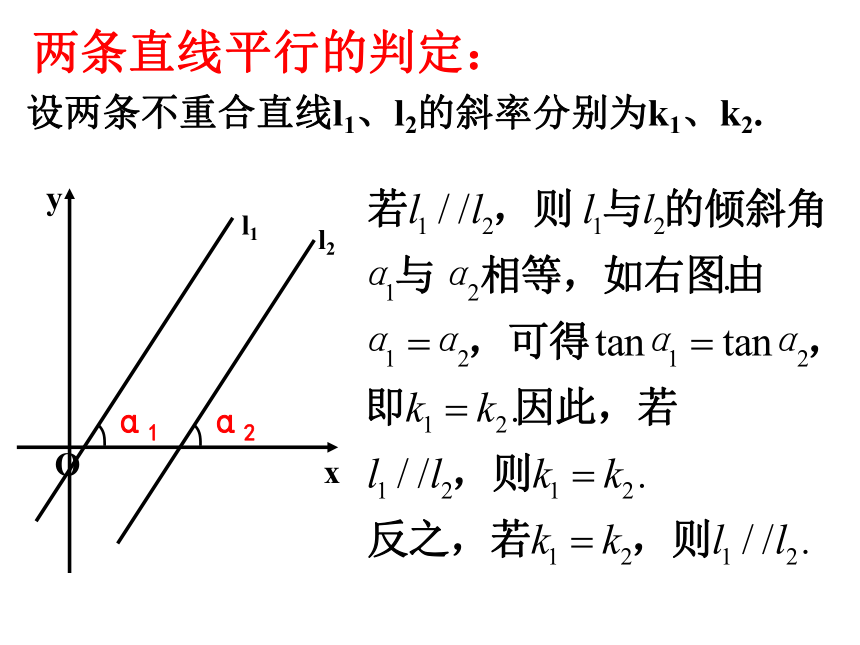
设两条不重合直线l1、l2的斜率分别为k1、k2.
x
O
y
l2
l1
α1
α2
两条直线平行的判定:
x
O
y
l2
l1
α1
α2
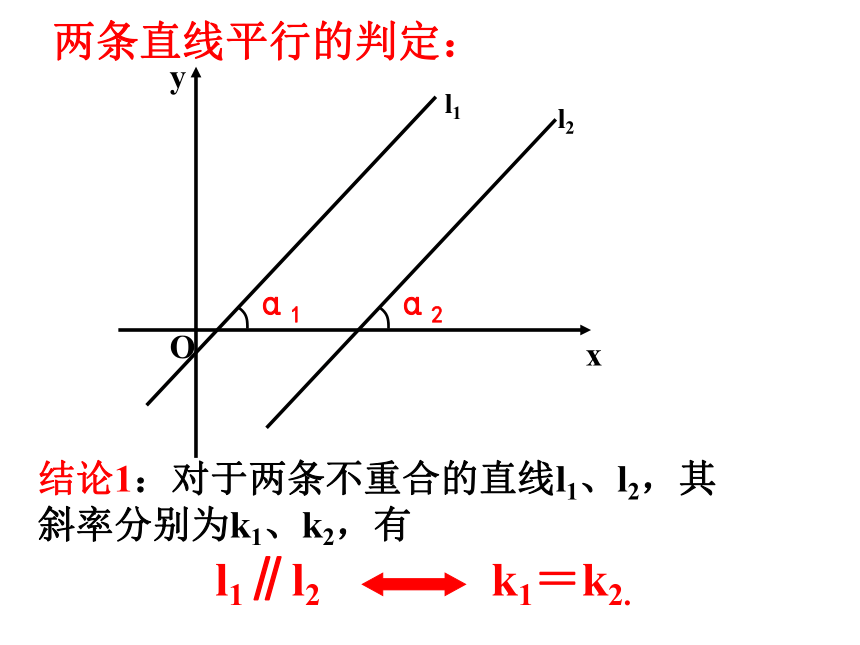
结论1:对于两条不重合的直线l1、l2,其斜率分别为k1、k2,有
l1∥l2 k1=k2.
两条直线平行的判定:
x
O
y
l2
l1
α1
α2
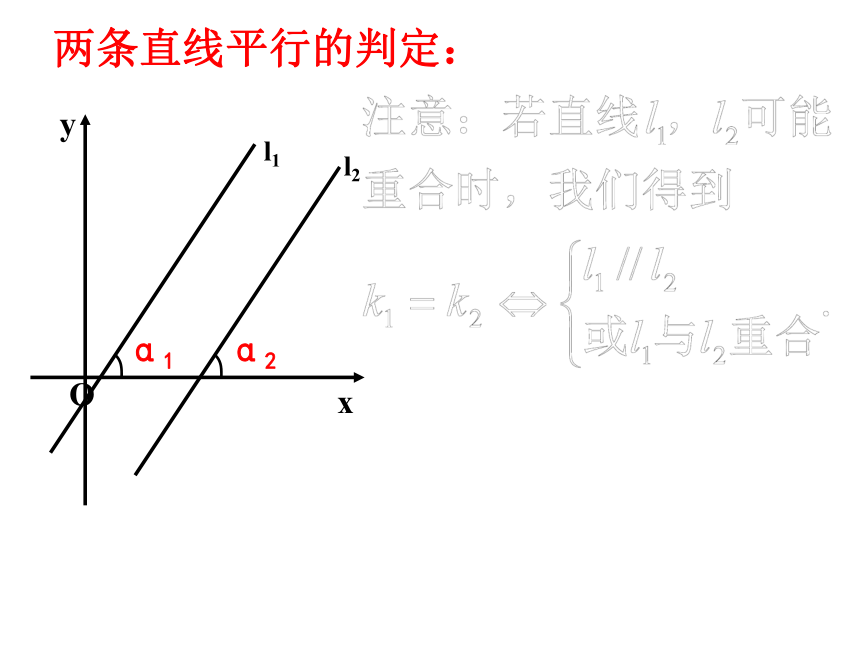
两条直线平行的判定:
例题讲解:
例3、已知A(2,3),B(-4,0),
P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
O
x
y
A
B
P
Q
∥
例4、已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
例题讲解:
O
x
y
D
C
A
B
∥
∥
设两条直线l1、l2的倾斜角分别为α1、α2( α1、α2≠90°).
x
O
y
l1
α1
l2
α2
两条直线垂直的判定:
设两条直线l1、l2的倾斜角分别为α1、α2( α1、α2≠90°).
x
O
y
l1
α1
l2
α2
结论2:如果两条直线l1、l2都有斜率,且分别为k1、k2,则有
l1⊥l2 k1k2=-1.
两条直线垂直的判定:
例5、已知A(-6,0),B(3,6),P(0,3) Q(6,-6),判断直线AB与PQ的位置关系。
例题讲解:
例题讲解:
例6、已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。
O
x
y
A
C
B
小结:结论1
如果直线L1,L2的斜率为k1,k2.
那么
注意:上面的等价是在两直线斜率存在的前提下才成立 的,缺少这个前提,结论并不存立.
特殊情况下的两直线平行:
两直线的倾斜角都为90°,互相平行.
或 L1与L2 重合
L1∥L2
k1=k2
?
知识点梳理
知识点梳理
结论2:
如果两直线的斜率为k1,,k2,那么
注意:上面的等价是在两直线斜率存在的前提下才成立的,缺少这个前提,结论并不存立.
特殊情况下的两直线垂直.
即两条直线中有一条直线没有斜率时,另一条直线的斜率为0时.
一条直线的倾斜角为900,另一条直线的倾斜角为0°,则 两直线互相垂直.
l1⊥l2 k1k2=-1.
1、已知直线l 的倾斜角是α,且450≤α≤1350,求直线的斜率k的取值范围。
练习:
2、已知直线l 的斜率是k,且0≤k≤1,求直线l的倾斜角α的取值范围。
3、 若三点A(5,1),B(a,3),C(-4,2)
在同一条直线上,确定常数a的值.
练习:
课堂练习:P89 1、2
课外作业:P89 习题3.1 A组6、7、8
B组 1、2、3、4、5、6
3.1.2 两条直线平行与垂直的判定
问题提出:
1.直线的倾斜角和斜率的含义分别是什么?
2.经过两点的直线的斜率公式是什么?
直线的倾斜程度
相对于x轴的倾斜程度
两条直线平行与垂直的判定
为了在平面直角坐标系内表示直线的倾斜程度,我们引入了直线倾斜角的概念,进而又引入了直线的斜率——表示直线相对于x轴的倾斜程度,并导出了计算斜率的公式,即把几何问题转化为代数问题.那么,我们能否通过直线的斜率,来判断两条直线的位置关系呢?
设两条不重合直线l1、l2的斜率分别为k1、k2.
x
O
y
l2
l1
α1
α2
两条直线平行的判定:
x
O
y
l2
l1
α1
α2
结论1:对于两条不重合的直线l1、l2,其斜率分别为k1、k2,有
l1∥l2 k1=k2.
两条直线平行的判定:
x
O
y
l2
l1
α1
α2
两条直线平行的判定:
例题讲解:
例3、已知A(2,3),B(-4,0),
P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论.
O
x
y
A
B
P
Q
∥
例4、已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
例题讲解:
O
x
y
D
C
A
B
∥
∥
设两条直线l1、l2的倾斜角分别为α1、α2( α1、α2≠90°).
x
O
y
l1
α1
l2
α2
两条直线垂直的判定:
设两条直线l1、l2的倾斜角分别为α1、α2( α1、α2≠90°).
x
O
y
l1
α1
l2
α2
结论2:如果两条直线l1、l2都有斜率,且分别为k1、k2,则有
l1⊥l2 k1k2=-1.
两条直线垂直的判定:
例5、已知A(-6,0),B(3,6),P(0,3) Q(6,-6),判断直线AB与PQ的位置关系。
例题讲解:
例题讲解:
例6、已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。
O
x
y
A
C
B
小结:结论1
如果直线L1,L2的斜率为k1,k2.
那么
注意:上面的等价是在两直线斜率存在的前提下才成立 的,缺少这个前提,结论并不存立.
特殊情况下的两直线平行:
两直线的倾斜角都为90°,互相平行.
或 L1与L2 重合
L1∥L2
k1=k2
?
知识点梳理
知识点梳理
结论2:
如果两直线的斜率为k1,,k2,那么
注意:上面的等价是在两直线斜率存在的前提下才成立的,缺少这个前提,结论并不存立.
特殊情况下的两直线垂直.
即两条直线中有一条直线没有斜率时,另一条直线的斜率为0时.
一条直线的倾斜角为900,另一条直线的倾斜角为0°,则 两直线互相垂直.
l1⊥l2 k1k2=-1.
1、已知直线l 的倾斜角是α,且450≤α≤1350,求直线的斜率k的取值范围。
练习:
2、已知直线l 的斜率是k,且0≤k≤1,求直线l的倾斜角α的取值范围。
3、 若三点A(5,1),B(a,3),C(-4,2)
在同一条直线上,确定常数a的值.
练习:
课堂练习:P89 1、2
课外作业:P89 习题3.1 A组6、7、8
B组 1、2、3、4、5、6
