高中数学人教A版必修2第四章4.2.3直线与圆的方程的应用课件(23张PPT)
文档属性
| 名称 | 高中数学人教A版必修2第四章4.2.3直线与圆的方程的应用课件(23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 309.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:29:55 | ||
图片预览






文档简介
4.2.3 直线与圆的方程的应用
情境问题:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域,已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
分析:以台风中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,其中,取10km为单位长度.
问题归结为圆O与直线l 是否有交点
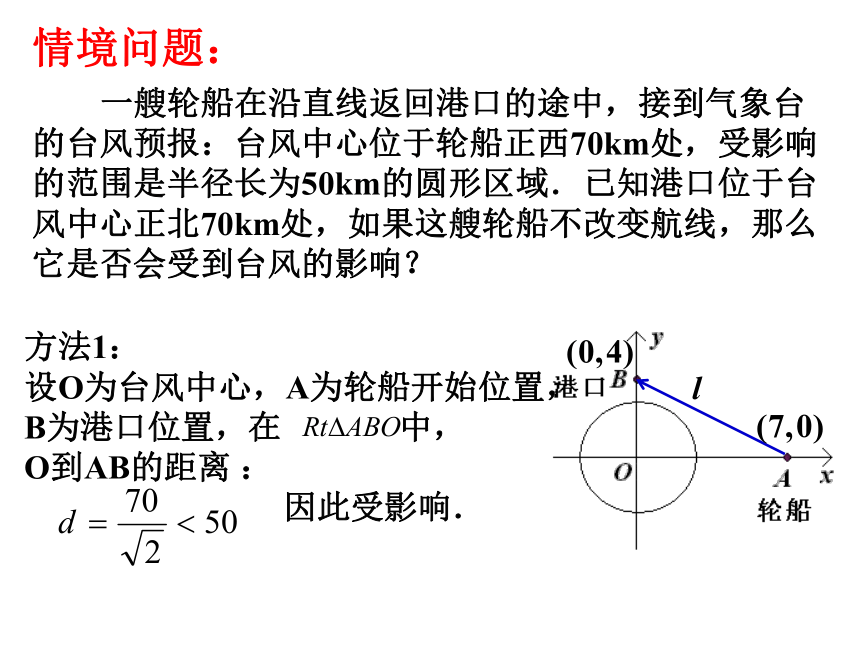
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为50km的圆形区域.已知港口位于台风中心正北70km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
情境问题:
方法1:
设O为台风中心,A为轮船开始位置,
B为港口位置,在 中,
O到AB的距离 :
因此受影响.
为解决这个问题,我们以台风中心为原点 O,东西方向为 x 轴,建立如图所示的直角坐标系,其中取 10km 为单位长度.
方法2:建立坐标系后,圆的方程0
,直线的方程
联立: 消元得:
方程组有两组解,相交
方法3:圆心到直线的距离 , 相交
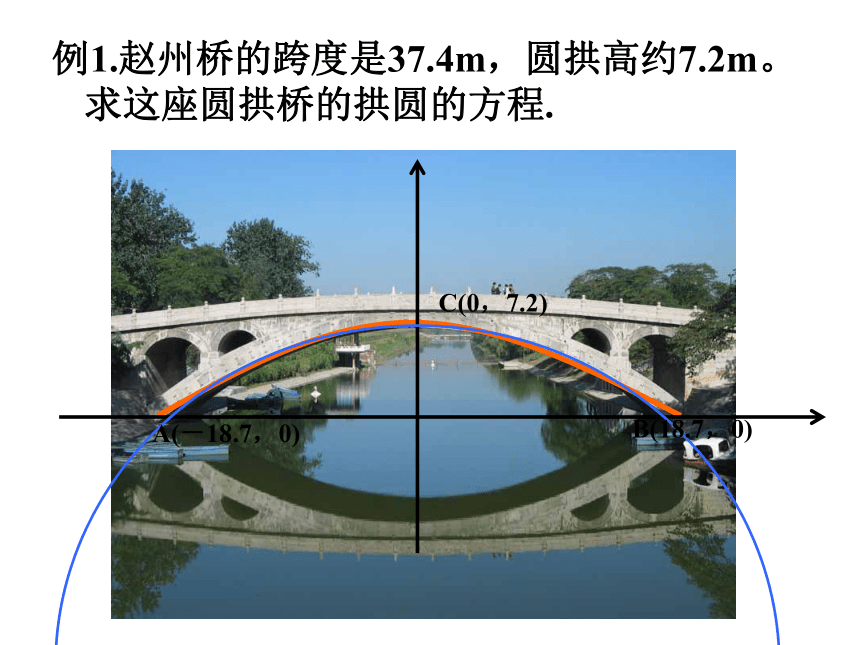
例1.赵州桥的跨度是37.4m,圆拱高约7.2m。求这座圆拱桥的拱圆的方程.
A(-18.7,0)
B(18.7,0)
C(0,7.2)
圆心在y轴上,并且过三个点A(-18.7,0), B(18.7,0),C(0,7.2).
解:设圆心坐标为(0,b),所以圆的方程为:
将B,C两点的坐标代入方程,得到方程组:
所以圆的方程为:
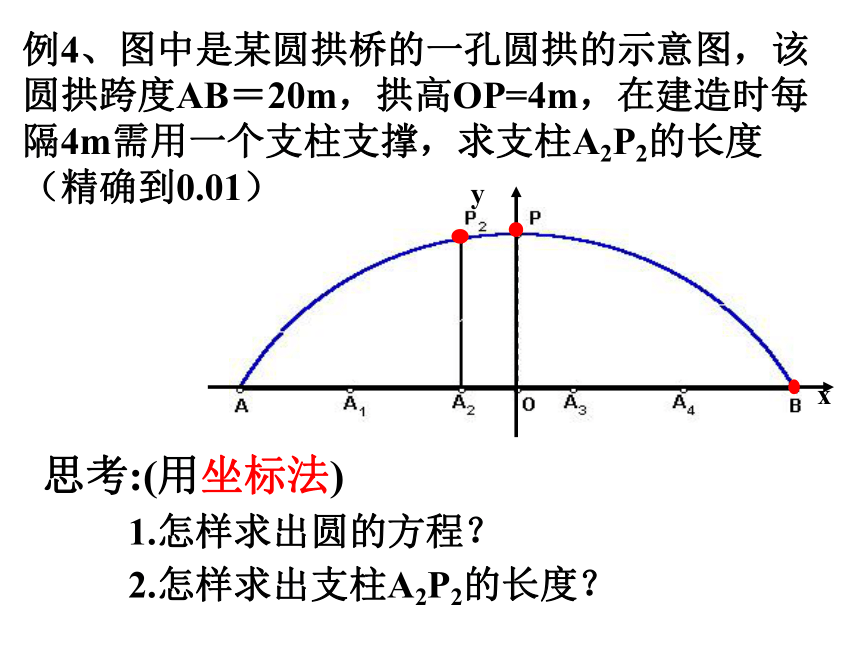
例4、图中是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01)
y
x
思考:(用坐标法)
1.怎样求出圆的方程?
2.怎样求出支柱A2P2的长度?
解:建立如图所示的坐标系,设圆心坐标是(0,b),
圆的半径是r ,则圆的方程是x2+(y-b)2=r2 .
把P(0,4) B(10,0)代入圆的方程得方程组:
02+(4-b)2= r2
102+(0-b)2=r2
解得, b= -10.5
r2=14.52
所以圆的方程是: x2+(y+10.5)2=14.52
把点P2的横坐标x= -2 代入圆的方程,得 (-2)2+(y+10.5)2=14.52
因为y>0,所以y=
14.52-(-2)2 -10.5≈14.36-10.5=3.86(m)
答:支柱A2P2的长度约为3.86m.
E
例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
E
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
E
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
E
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
o
y
x
(6,0)
(2,0)
(0,0)
A
B
D
C
E
P
o
y
x
(6,0)
(2,0)
(0,0)
A
B
D
C
E
P
o
y
x
(6,0)
(2,0)
(0,0)
A
B
D
C
E
P
用坐标法解决平面几何问题的步骤:
第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算结果“翻译”成几何结论.
练习:
1、求直线l: 2x-y-2=0被圆C: (x-3)2+y2=0所截得的弦长.
2、某圆拱桥的水面跨度20 m,拱高4 m. 现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?
5
O
M
N
P
练习:
3、点M在圆心为C1的方程:
x2+y2+6x-2y+1=0,点N在圆心为C2的方程x2+y2+2x+4y+1=0,求|MN|的最大值.
课堂练习:P132
练习 1、2、3、4
课外作业:P133 B组 1、2、3、4、5
情境问题:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域,已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
分析:以台风中心为原点O,东西方向为x轴,建立如图所示的直角坐标系,其中,取10km为单位长度.
问题归结为圆O与直线l 是否有交点
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为50km的圆形区域.已知港口位于台风中心正北70km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
情境问题:
方法1:
设O为台风中心,A为轮船开始位置,
B为港口位置,在 中,
O到AB的距离 :
因此受影响.
为解决这个问题,我们以台风中心为原点 O,东西方向为 x 轴,建立如图所示的直角坐标系,其中取 10km 为单位长度.
方法2:建立坐标系后,圆的方程0
,直线的方程
联立: 消元得:
方程组有两组解,相交
方法3:圆心到直线的距离 , 相交
例1.赵州桥的跨度是37.4m,圆拱高约7.2m。求这座圆拱桥的拱圆的方程.
A(-18.7,0)
B(18.7,0)
C(0,7.2)
圆心在y轴上,并且过三个点A(-18.7,0), B(18.7,0),C(0,7.2).
解:设圆心坐标为(0,b),所以圆的方程为:
将B,C两点的坐标代入方程,得到方程组:
所以圆的方程为:
例4、图中是某圆拱桥的一孔圆拱的示意图,该圆拱跨度AB=20m,拱高OP=4m,在建造时每隔4m需用一个支柱支撑,求支柱A2P2的长度(精确到0.01)
y
x
思考:(用坐标法)
1.怎样求出圆的方程?
2.怎样求出支柱A2P2的长度?
解:建立如图所示的坐标系,设圆心坐标是(0,b),
圆的半径是r ,则圆的方程是x2+(y-b)2=r2 .
把P(0,4) B(10,0)代入圆的方程得方程组:
02+(4-b)2= r2
102+(0-b)2=r2
解得, b= -10.5
r2=14.52
所以圆的方程是: x2+(y+10.5)2=14.52
把点P2的横坐标x= -2 代入圆的方程,得 (-2)2+(y+10.5)2=14.52
因为y>0,所以y=
14.52-(-2)2 -10.5≈14.36-10.5=3.86(m)
答:支柱A2P2的长度约为3.86m.
E
例5、已知内接于圆的四边形的对角线互相垂直,求证圆心到一边的距离等于这条边所对边长的一半.
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
E
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
E
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
E
x
y
O
C
A
B
D
(a,0)
(0,b)
(c,0)
(0,d)
O`
M
N
o
y
x
(6,0)
(2,0)
(0,0)
A
B
D
C
E
P
o
y
x
(6,0)
(2,0)
(0,0)
A
B
D
C
E
P
o
y
x
(6,0)
(2,0)
(0,0)
A
B
D
C
E
P
用坐标法解决平面几何问题的步骤:
第一步:建立适当的坐标系,用坐标和方程表示问题中的几何元素,将平面几何问题转化为代数问题;
第二步:通过代数运算,解决代数问题;
第三步:把代数运算结果“翻译”成几何结论.
练习:
1、求直线l: 2x-y-2=0被圆C: (x-3)2+y2=0所截得的弦长.
2、某圆拱桥的水面跨度20 m,拱高4 m. 现有一船,宽10 m,水面以上高3 m,这条船能否从桥下通过?
5
O
M
N
P
练习:
3、点M在圆心为C1的方程:
x2+y2+6x-2y+1=0,点N在圆心为C2的方程x2+y2+2x+4y+1=0,求|MN|的最大值.
课堂练习:P132
练习 1、2、3、4
课外作业:P133 B组 1、2、3、4、5
