高中数学人教A版必修4第二章:2.3.4平面向量共线的坐标表示课件(15张PPT)
文档属性
| 名称 | 高中数学人教A版必修4第二章:2.3.4平面向量共线的坐标表示课件(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 324.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:31:56 | ||
图片预览






文档简介
2.3.4平面向量共线的坐标表示
2.平面向量的坐标运算:
1.向量共线充要条件:
复习回顾:
注:向量坐标等于终点坐标减去起点坐标
例5.如图,已知 的三个顶点A、B、C的坐标分别是
(-2,1)、(-1,3)、(3,4),试求顶点D的坐标。
A
B
C
D
x
y
O
解:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
向量共线的条件用坐标表示:
已知a ,b
∥
注意:
不能写成
,因为
有可能为0;
如何用坐标表示两个共线向量?
例7.已知 A(-1,-1),B(1,3),C(2,5),试判断A、B、C三点
之间的位置关系。
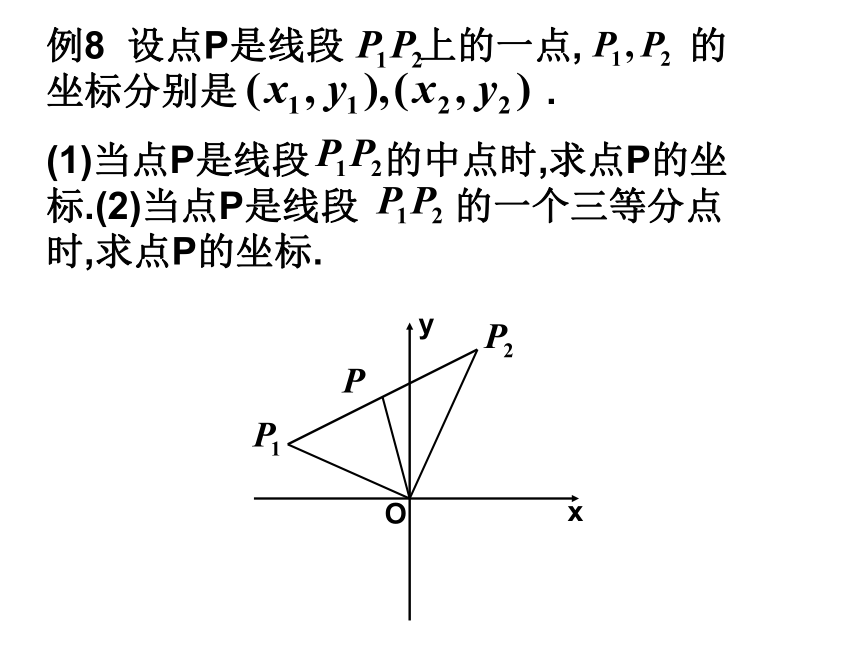
例8 设点P是线段 上的一点, 的坐标分别是 .
(1)当点P是线段 的中点时,求点P的坐标.(2)当点P是线段 的一个三等分点时,求点P的坐标.
O
x
y
结论:中点坐标公式:
x
y
O
P1
P2
P
x
y
O
P1
P2
P
O
x
y
探究
设点P是线段 上(或延长线上)的一点, 的坐标分别是 .
结论:线段定比分点坐标公式:
练习
P100—101 :
第4、5、6、7题
作业布置
P101 A组:
第1、3、4、5 、6、7题
课堂小结
一.向量共线的条件:
∥
(1)
存在唯一实数λ,使
∥
(2)
已知a ,b
二.中点坐标公式:
三.线段定比分点坐标公式:
2
1
PP
P
P
l
=
练习巩固
坐标是
A、(3,2) B、(2,3) C、(-3,-2) D、(-2,-3)
B
A、x=1,y=3 B、x=3,y=1
C、x=1,y=-3 D、x=5,y=-1
B
标
坐标为
A、(x-2,y+1) B、(x+2,y-1)
C、(-2-x,1-y) D、(x+2,y+1)
C
B
B
标
的坐标为(i,j),则点A
的坐标为
A、(m-i,n-j) B、(i-m,j-n)
C、(m+i,n+j) D、(m+n,i+j)
A
2.平面向量的坐标运算:
1.向量共线充要条件:
复习回顾:
注:向量坐标等于终点坐标减去起点坐标
例5.如图,已知 的三个顶点A、B、C的坐标分别是
(-2,1)、(-1,3)、(3,4),试求顶点D的坐标。
A
B
C
D
x
y
O
解:设点D的坐标为(x,y)
解得 x=2,y=2
所以顶点D的坐标为(2,2)
向量共线的条件用坐标表示:
已知a ,b
∥
注意:
不能写成
,因为
有可能为0;
如何用坐标表示两个共线向量?
例7.已知 A(-1,-1),B(1,3),C(2,5),试判断A、B、C三点
之间的位置关系。
例8 设点P是线段 上的一点, 的坐标分别是 .
(1)当点P是线段 的中点时,求点P的坐标.(2)当点P是线段 的一个三等分点时,求点P的坐标.
O
x
y
结论:中点坐标公式:
x
y
O
P1
P2
P
x
y
O
P1
P2
P
O
x
y
探究
设点P是线段 上(或延长线上)的一点, 的坐标分别是 .
结论:线段定比分点坐标公式:
练习
P100—101 :
第4、5、6、7题
作业布置
P101 A组:
第1、3、4、5 、6、7题
课堂小结
一.向量共线的条件:
∥
(1)
存在唯一实数λ,使
∥
(2)
已知a ,b
二.中点坐标公式:
三.线段定比分点坐标公式:
2
1
PP
P
P
l
=
练习巩固
坐标是
A、(3,2) B、(2,3) C、(-3,-2) D、(-2,-3)
B
A、x=1,y=3 B、x=3,y=1
C、x=1,y=-3 D、x=5,y=-1
B
标
坐标为
A、(x-2,y+1) B、(x+2,y-1)
C、(-2-x,1-y) D、(x+2,y+1)
C
B
B
标
的坐标为(i,j),则点A
的坐标为
A、(m-i,n-j) B、(i-m,j-n)
C、(m+i,n+j) D、(m+n,i+j)
A
