高中数学人教A版必修5第三章3.4基本不等式课件(共16张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章3.4基本不等式课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览




文档简介
§3.4基本不等式
2002年国际数学家大会会标
创设情境、体会感知:
三国时期吴国的数学家赵爽
思考:这会标中含有怎样的几何图形?
思考:你能否在这个图案中找出一些相等关系或不等关系?
一 、探究
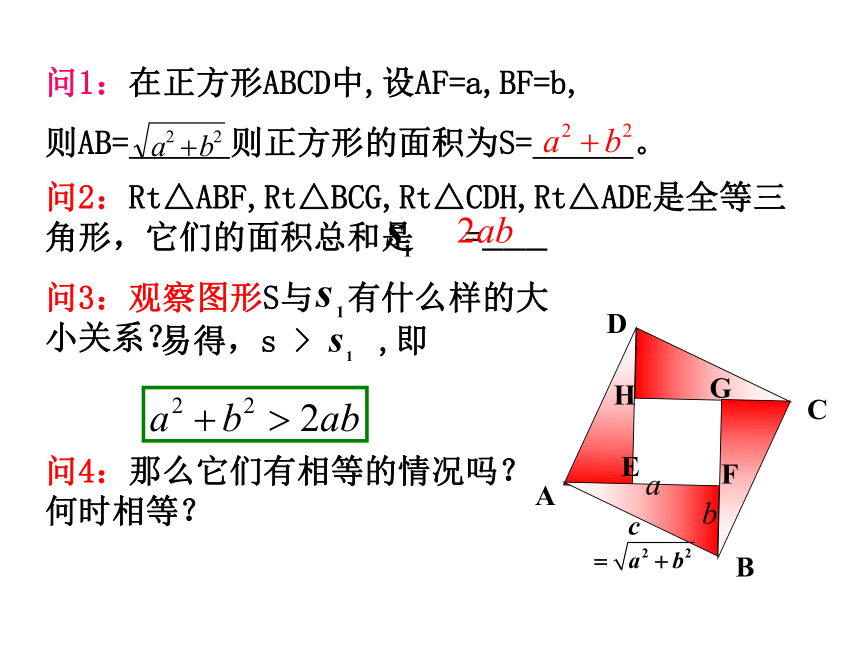
问1:在正方形ABCD中,设AF=a,BF=b,
则AB= 则正方形的面积为S= 。
问2:Rt△ABF,Rt△BCG,Rt△CDH,Rt△ADE是全等三角形,它们的面积总和是 =———
问3:观察图形S与 有什么样的大小关系?
易得,s > ,即
A
D
C
B
H
G
F
E
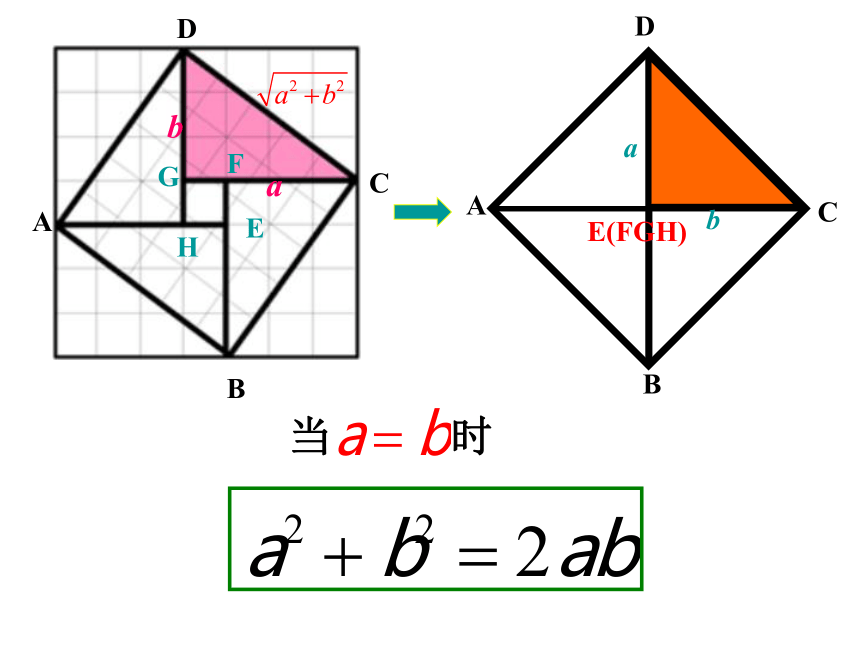
问4:那么它们有相等的情况吗?
何时相等?
A
D
B
C
E
F
G
H
b
a
A
B
C
D
E(FGH)
a
b
当 时
结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立
问5:当a,b为任意实数时,
还成立吗?
形
数
此不等式称为重要不等式
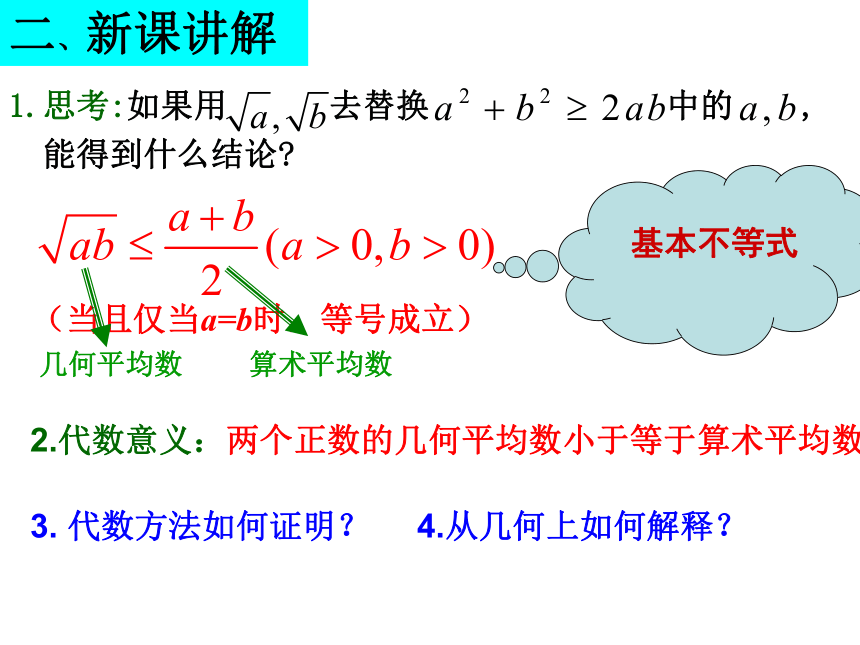
2.代数意义:两个正数的几何平均数小于等于算术平均数
(当且仅当a=b时,等号成立)
二、新课讲解
1.思考:如果用 去替换 中的 ,
能得到什么结论?
算术平均数
几何平均数
基本不等式
3. 代数方法如何证明?
4.从几何上如何解释?
证明:要证
只要证
( )
①
②
要证②,只要证
( )
③
要证③,只要证( - )
④
显然: 是成立的,当且仅当 时
④
④
中的等号成立.
证明:当 时, .
分析法
代数方法:
o
a
b
A
B
P
Q
如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则半弦PQ=____,半径AO=_____
几何意义:圆的半径不小于圆内半弦长
你能用这个图得出基本不等式的几何解释吗?
几何方法:
2.基本不等式:
当且仅当a =b时,等号成立.
当且仅当a=b时,等号成立.
1.重要不等式:
(1)不同点:两个不等式的适用条件不同。
(2)相同点:当且仅当a=b时,等号成立。
知识要点:
(3)不等式的简单应用:主要在于求最值
把握 “七字方针” 即 “一正,二定,三相等”
三、应用
当两正数积为定值时,求其和的最小值
练习2:若 求 的最小值.
例1、(1)若 求 的最小值.
( 2 ) 若 求 的最大值.
练习1:若 求 的最小值.
练习3:设a>0,b>0,证明下列不等式
例2:若 ,求 的最小值.
构造条件
1、本节课主要内容?
你会了吗?
谢 谢!
1.设 >0, >0,若 是 与 的等比中项,则
得最小值为( )
A. 8 B. 4 C. 1 D.
B
x>0, 当x取何值时, 的值最小?最小值是多少?
已知直角三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小,最小值是多少?
用20cm长的铁丝折成一个面积最大的矩形,应怎样折?
作业
(课本100页)
2002年国际数学家大会会标
创设情境、体会感知:
三国时期吴国的数学家赵爽
思考:这会标中含有怎样的几何图形?
思考:你能否在这个图案中找出一些相等关系或不等关系?
一 、探究
问1:在正方形ABCD中,设AF=a,BF=b,
则AB= 则正方形的面积为S= 。
问2:Rt△ABF,Rt△BCG,Rt△CDH,Rt△ADE是全等三角形,它们的面积总和是 =———
问3:观察图形S与 有什么样的大小关系?
易得,s > ,即
A
D
C
B
H
G
F
E
问4:那么它们有相等的情况吗?
何时相等?
A
D
B
C
E
F
G
H
b
a
A
B
C
D
E(FGH)
a
b
当 时
结论:一般地,对于任意实数a、b,我们有
当且仅当a=b时,等号成立
问5:当a,b为任意实数时,
还成立吗?
形
数
此不等式称为重要不等式
2.代数意义:两个正数的几何平均数小于等于算术平均数
(当且仅当a=b时,等号成立)
二、新课讲解
1.思考:如果用 去替换 中的 ,
能得到什么结论?
算术平均数
几何平均数
基本不等式
3. 代数方法如何证明?
4.从几何上如何解释?
证明:要证
只要证
( )
①
②
要证②,只要证
( )
③
要证③,只要证( - )
④
显然: 是成立的,当且仅当 时
④
④
中的等号成立.
证明:当 时, .
分析法
代数方法:
o
a
b
A
B
P
Q
如图,AB是圆o的直径,Q是AB上任一点,AQ=a,BQ=b,过点Q作垂直于AB的弦PQ,连AP,BP,
则半弦PQ=____,半径AO=_____
几何意义:圆的半径不小于圆内半弦长
你能用这个图得出基本不等式的几何解释吗?
几何方法:
2.基本不等式:
当且仅当a =b时,等号成立.
当且仅当a=b时,等号成立.
1.重要不等式:
(1)不同点:两个不等式的适用条件不同。
(2)相同点:当且仅当a=b时,等号成立。
知识要点:
(3)不等式的简单应用:主要在于求最值
把握 “七字方针” 即 “一正,二定,三相等”
三、应用
当两正数积为定值时,求其和的最小值
练习2:若 求 的最小值.
例1、(1)若 求 的最小值.
( 2 ) 若 求 的最大值.
练习1:若 求 的最小值.
练习3:设a>0,b>0,证明下列不等式
例2:若 ,求 的最小值.
构造条件
1、本节课主要内容?
你会了吗?
谢 谢!
1.设 >0, >0,若 是 与 的等比中项,则
得最小值为( )
A. 8 B. 4 C. 1 D.
B
x>0, 当x取何值时, 的值最小?最小值是多少?
已知直角三角形的面积等于50,两条直角边各为多少时,两条直角边的和最小,最小值是多少?
用20cm长的铁丝折成一个面积最大的矩形,应怎样折?
作业
(课本100页)
