高中数学人教A版必修二2.2.4平面与平面平行的性质 课件(共38张PPT))
文档属性
| 名称 | 高中数学人教A版必修二2.2.4平面与平面平行的性质 课件(共38张PPT)) |

|
|
| 格式 | ppt | ||
| 文件大小 | 432.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:33:40 | ||
图片预览




文档简介
2.2.4 平面与平面平行的性质
2.2 直线、平面平
行的判定及其性质
教学目标:
:1、掌握平面与平面平行的性质定理.明确由面面平行可推出线面平行.
2、结合具体问题体会空间与平面的转化关系.
问题提出:
1.平面与平面平行的判定定理是什么?
2.平面与平面平行的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的条件下,可以得到什么结论呢?
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
平面与平面平行的性质
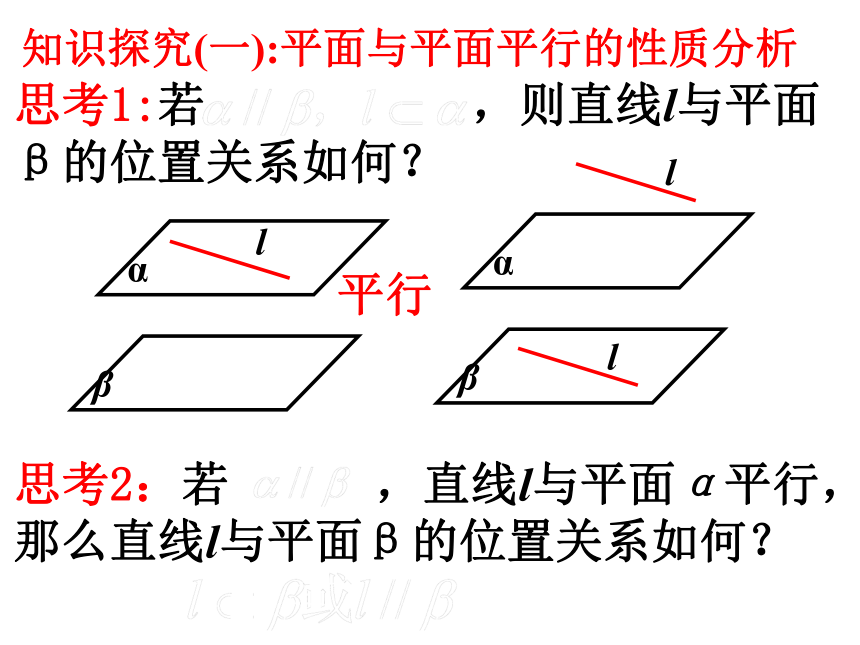
知识探究(一):平面与平面平行的性质分析
思考1:若 ,则直线l与平面β的位置关系如何?
l
β
α
思考2:若 ,直线l与平面α平行,那么直线l与平面β的位置关系如何?
l
平行
β
α
l
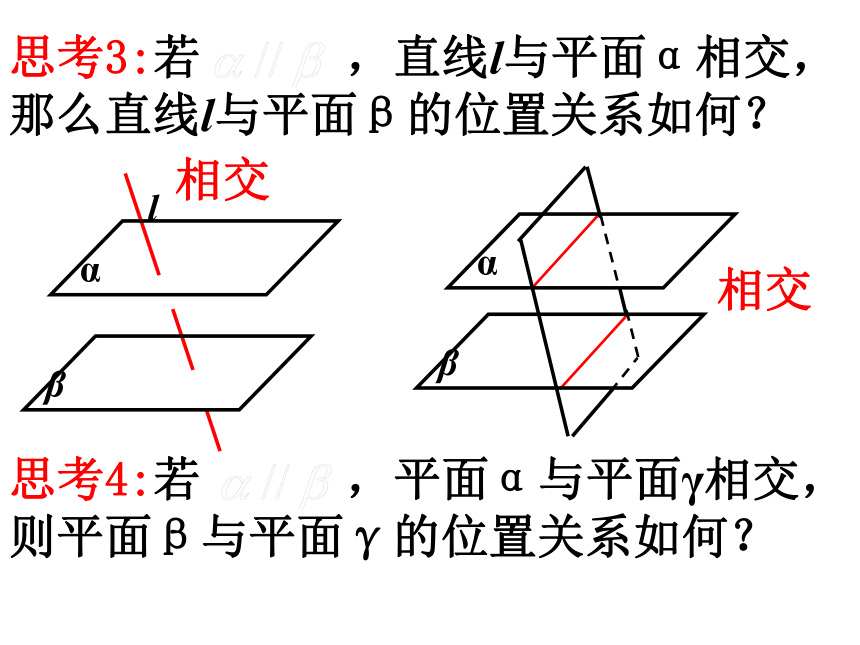
思考4:若 ,平面α与平面γ相交,则平面β与平面γ的位置关系如何?
思考3:若 ,直线l与平面α相交,那么直线l与平面β的位置关系如何?
l
β
α
β
α
相交
相交
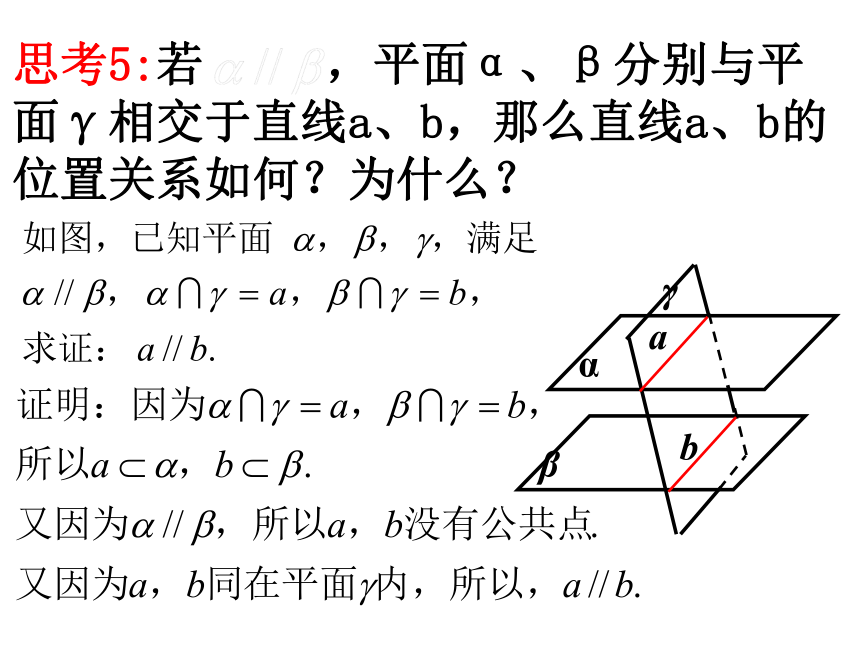
思考5:若 ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?
β
α
γ
a
b
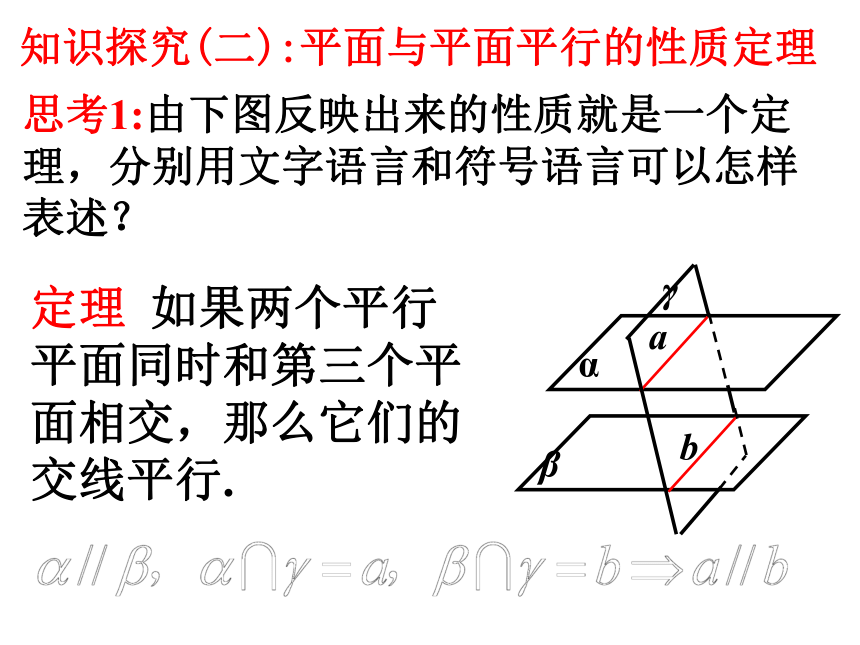
知识探究(二):平面与平面平行的性质定理
思考1:由下图反映出来的性质就是一个定理,分别用文字语言和符号语言可以怎样表述?
定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
β
α
a
b
γ
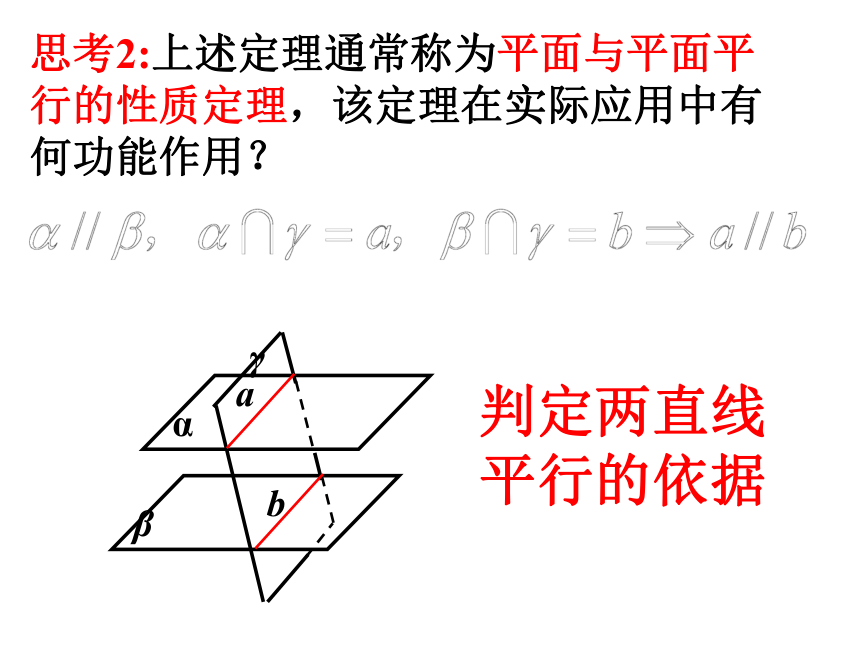
思考2:上述定理通常称为平面与平面平行的性质定理,该定理在实际应用中有何功能作用?
判定两直线平行的依据
β
α
γ
a
b
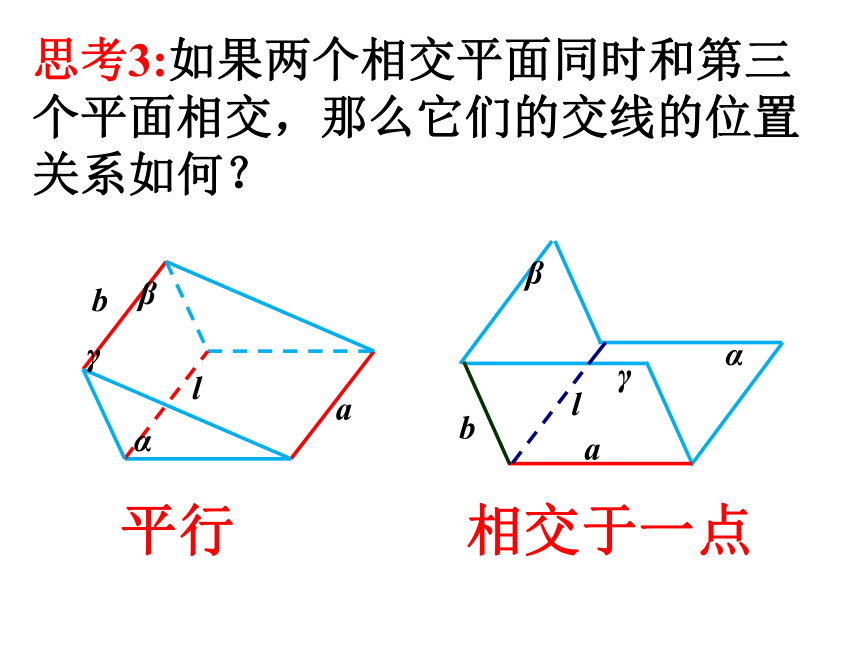
思考3:如果两个相交平面同时和第三个平面相交,那么它们的交线的位置关系如何?
α
β
γ
a
b
l
α
β
γ
a
b
l
平行
相交于一点
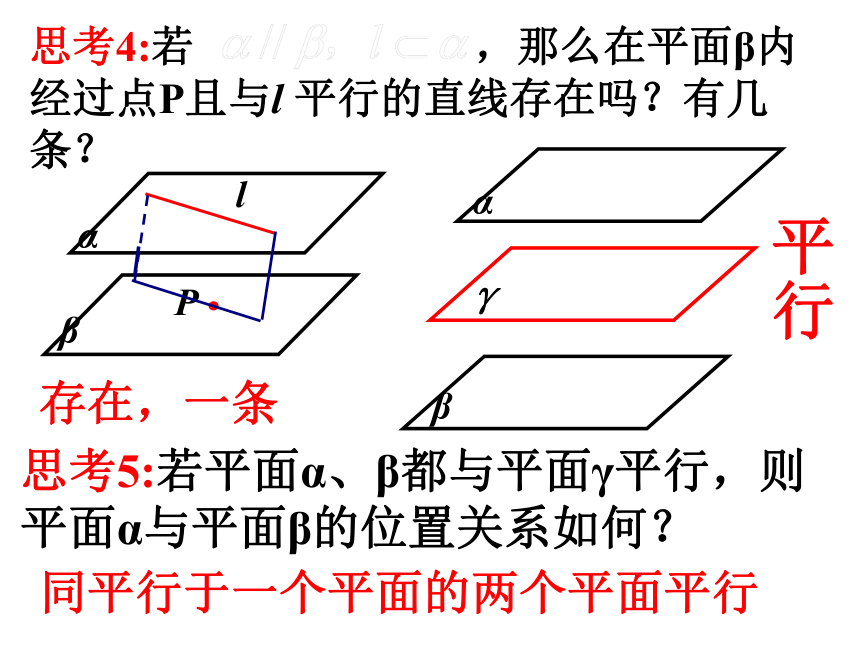
思考4:若 ,那么在平面β内经过点P且与l 平行的直线存在吗?有几条?
l
β
α
P
思考5:若平面α、β都与平面γ平行,则平面α与平面β的位置关系如何?
β
α
γ
存在,一条
平行
同平行于一个平面的两个平面平行
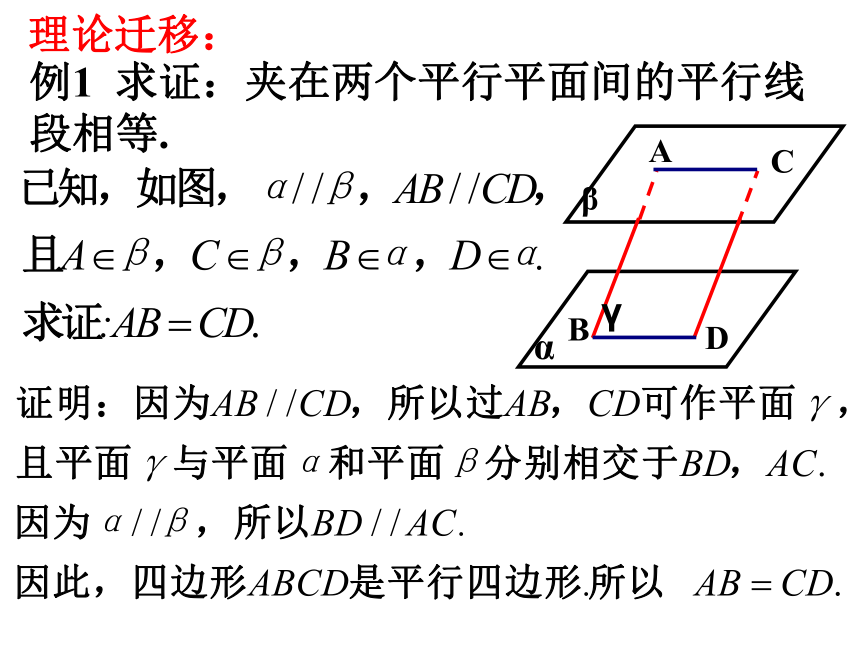
理论迁移:
例1 求证:夹在两个平行平面间的平行线段相等.
α
β
D
B
A
C
γ
面面平行的性质定理的几个常用结论:
(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面;
(2)夹在两个平行平面之间的平行线段相等;
(3)经过平面外一点有且只有一个平面与已知平面平行;
(4)两条直线被三个平行平面所截,截得的对应线段成比例 ;
(5)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
例2 在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线B′M与平面A′BD的位置关系,并说明理由.
A′
B′
C′
D′
A
B
C
D
M
平行
例3 如图,已知AB、CD是夹在两个平行
平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面β.
M
N
A
B
C
D
E
l
β
α
基础强化:
1.已知直线a∥平面α,则a与平面α内的直线的位置关系为( )
A.相交 B.平行 C.异面或平行 D.异面
C
2.已知m?n表示两条直线,α?β?γ表示平面,下列命题中正确的个数是( )
①若α∩γ=m,β∩γ=n,且m∥n,则α∥β;
②若m?n相交且都在α外,m∥α,m∥β,n∥α,
n∥β,则α∥β;
③若m∥α,m∥β,则α∥β;
④若m∥α,n∥β,且m∥n,则α∥β.
A.1 B.2 C.3 D.4
解析:∵直线m与n相交,∴m与n确定一个平面π,
又m∥α,n∥α,∴α∥π,同理β∥π,∴α∥β.故②正确.其它均错.故选A.
A
3.已知平面α∥β,P是α?β外一点,过点P的直线m与α?β分别交于A?C,过点P的直线n与α?β分别交于B?D,且PA=6,AC=9,PD=8,则BD的长为( )
解析:当点P在平面α与β的同侧时,由平行线截线段成比例知
当P在平面α与β之间时,同理可求得BD=24.
B
4.α?β?γ是三个两两平行的平面,且α与β之间的距离是3,α与γ之间的距离是4,则β与γ之间的距离的取值范围是( )
A.{1} B.{7} C.{1,7} D.[1,7]
C
5.已知平面α∥平面β,它们之间的距离为d,直线
a α,则在β内与直线a相距为2d的直线有( )
A.一条 B.两条 C.无数条 D.不存在
B
6.给出下列互不相同的直线l?m?n和平面α?β?γ的三个命题:
①若l与m为异面直线,l α,m β,则α∥β.
②若α∥β,l α,m β,则l∥m.
③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
其中真命题的个数为( )
A.3 B.2 C.1 D.0
解析:①中α与β也可能相交.∴①错;在②中l与m也可能异面,∴②错.③正确.
C
7.已知直线l∥平面α,设A∈l,B∈l,C∈α,D∈α,且AC∥BD.则AC________BD(填“=”或“≠”).
8.过正方体ABCD—A1B1C1D1的三顶点A1?C1?B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是__________.
=
平行
9.如下图,两条异面直线AC?DF与三个平行平面α?β?γ分别交于A?B?C和D?E?F,又AF?CD分别与β交于G?H,求证:HEGB是平行四边形.
能力提升
证明:∵AC∩CD=C,
∴AC?CD确定平面ACD.
又α∥β,平面ACD与α?β交于AD?BH,∴AD∥BH.又AF∩DF=F,
∴AF?FD确定平面AFD.
又∵α∥β,平面AFD交α?β于AD?GE,∴AD∥GE.∴BH∥GE.
同理BG∥HE.
∴四边形HEGB是平行四边形.
10.如图(1)所示,在空间六边形(即六个顶点中没有任何五点共面)ABCC1D1A1中,每相邻的两边互相垂直,边长均等于a,并且AA1∥CC1.
求证:平面A1BC1∥平面ACD1.
分析:由本题的条件不难联想到正方体,从而用补形法证之.
证明:首先将图形补成正方体框架,如下图(2)所示.
则在正方体ABCD-A1B1C1D1中,证平面A1BC1∥平面ACD1.
由正方体的性质易知,AC∥A1C1.
∴AC∥平面A1BC1,同理
可证CD1∥平面A1BC1.
又AC∩CD1=C,
∴平面A1BC1∥平面ACD1.
11.过平行六面体ABCD—A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有( )
A.4条 B.6条 C.8条 D.12条
解析:如图取各棱的中点.
D
易证平面EFGH∥平面 ,故平行四边形EFGH的四条边及对角线均为各棱中点的连线均平行于面 ,共6条,同理在平行四边形JKMN中也有6条满足条件,故共有12条.
12.如图,在四面体ABCD中,CB=CD,AD⊥BD,且E?F分别是AB?BD的中点.
求证:直线EF∥面ACD.
证明:在△ABD中,
∵E?F分别是AB?BD的中点,
∴EF∥AD.
又AD 平面ACD,
EF 平面ACD,
∴直线EF∥面ACD.
题型一 证明线面平行
例1.在正方体ABCD-A1B1C1D1中,E为CD的中点,F为B1C1的中点.
求证:EF∥平面BB1D1D.
分析:如右图所示.
要证线面平行,可先证面面平行,取BC的中点H,连结FH?EH.
易证平面EFH∥平面 .
再用两面平行的性质得证.
证明:如上图,取BC的中点H.连结EH,FH.∵E为CD的中点.
∴EH∥BD,EH 平面 .∴EH∥平面 .
又F为 的中点.∴ BH,∴ 为平行四边形,
∴FH∥ ,又FH 平面 .∴FH∥平面 .
又FH∩EH=H,∴平面EFH∥平面 .
∴EF∥平面 .
规律技巧:在证明线面平行时,常用:线线平行,线面平行,面面平行进行相互转化,达到证题的目的.
变式训练1:如图所示,直三棱柱ABC—A1B1C1底面为等腰直角三角形,∠ABC=90°, P?Q分别为A1B和CC1的中点。求证:PQ∥平面A1B1C1.
证法一:如图(1)所示,取A1B1的中点D,连结DP?DC1,则有DP? .
又Q为CC1的中点,
∴DP? QC1.
∴四边形PQC1D是平行四边形,
∴PQ∥C1D.
又PQ 平面A1B1C1,
C1D 平面A1B1C1,
∴PQ∥平面A1B1C1.
证法二:如图(2)所示,取BB1的中点E,连结EP?EQ,则有PE∥A1B1,QE∥B1C1.
又PE 平面A1B1C1,QE 平面A1B1C1,A1B1 平面A1B1C1,B1C1 平面A1B1C1,
∴PE∥平面A1B1C1,QE∥平面A1B1C1.
又PE 平面PQE,QE 平面PQE,PE∩QE=E,
∴平面PQE∥平面A1B1C1.
又PQ 平面PQE,
∴PQ∥平面A1B1C1.
题型二 证明面面平行
例2.已知a,b是异面直线,a 平面α,b 平面β,a∥β,b∥α,求证:α∥β.
分析:要证α∥β,由判定定理知,在β内找出两
条相交直线都平行于α.由已知,b β,b∥α,
再找出一条直线a′∥α.这需要作辅助平面γ,
使γ∩α=a,γ∩β=a′,只要a′∥a,就可得
α∥β,具体如何作出辅助平面γ,请看证明.
证明:在b上任取一点P,设直线a与点P确定平面为γ,如下图所示.
设β∩γ=a′,∵a∥β,∴a′∥a,∴a′∥α.
又b∥α,且a′∩b=P,a′ β,b β,
∴α∥β.
变式训练2.已知:平面α∥平面β,平面β∥平面γ.
求证:α∥γ.
证明:如图,作两个相交平面分别与α?β?γ交于a?c?e
和b?d?f.
∵α∥β,
∴a∥c,b∥d.
又β∥γ,∴c∥e,d∥f.
∴a∥e,b∥f,又a与b相交,
∴α∥γ.
题型三 综合性问题
例3.如下图,在三棱柱ABC—A1B1C1中,点D?D1分别为AC?A1C1上的点.
(1)当 的值等于何值时,
BC1∥平面AB1D1;
(2)若平面BC1D∥平面AB1D1,
求 的值.
分析:若BC1∥平面AB1D1,则平面AB1D1中存在直线与BC1平行,连结A1B交AB1于O,由棱柱的定义知O为A1B的中点,平面A1BC1与平面AB1D1的交线OD1与直线BC1平行,由
三角形中位线定理知D1为
A1C1的中点,此时
若平面BC1D∥平面AB1D1,
易知
解:(1)如下图,取D1为线段A1C1的中点,此时
连结A1B交AB1于点O,连结OD1.
由棱柱的定义,知四边形A1ABB1为平行四边形,所以点O为A1B的中点.
在△A1BC1中,点O?D1分别为A1B?A1C1的中点,∴OD1∥BC1.
又∵OD1 平面AB1D1,BC1 平面AB1D1,
∴BC1∥平面AB1D1.
∴ 时,BC1∥平面AB1D1.
(2)由已知,平面BC1D∥平面AB1D1.
且平面A1BC1∩平面BDC1=BC1,
平面A1BC1∩平面AB1D1=D1O,
因此BC1∥D1O,同理AD1∥DC1.
规律技巧:探索平行问题,即找平行成立具备的条件,
三种平行关系的相互转化是解决问题常用的方法.
变式训练3.如图,已知α∥β,P是平面α,β外的一点,直线PAB,PCD分别与α?β相交于A?B和C?D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
(1)证明:∵PB∩PD=P,∴直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD,又α∥β,∴AC∥BD.
(2)解:由(1)得AC∥BD,
作业:
P61练习:(做在书上)
P63习题2.2B组:4(做在书上)
P63习题2.2B组:3.
2.2 直线、平面平
行的判定及其性质
教学目标:
:1、掌握平面与平面平行的性质定理.明确由面面平行可推出线面平行.
2、结合具体问题体会空间与平面的转化关系.
问题提出:
1.平面与平面平行的判定定理是什么?
2.平面与平面平行的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的条件下,可以得到什么结论呢?
定理 如果一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.
平面与平面平行的性质
知识探究(一):平面与平面平行的性质分析
思考1:若 ,则直线l与平面β的位置关系如何?
l
β
α
思考2:若 ,直线l与平面α平行,那么直线l与平面β的位置关系如何?
l
平行
β
α
l
思考4:若 ,平面α与平面γ相交,则平面β与平面γ的位置关系如何?
思考3:若 ,直线l与平面α相交,那么直线l与平面β的位置关系如何?
l
β
α
β
α
相交
相交
思考5:若 ,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?
β
α
γ
a
b
知识探究(二):平面与平面平行的性质定理
思考1:由下图反映出来的性质就是一个定理,分别用文字语言和符号语言可以怎样表述?
定理 如果两个平行平面同时和第三个平面相交,那么它们的交线平行.
β
α
a
b
γ
思考2:上述定理通常称为平面与平面平行的性质定理,该定理在实际应用中有何功能作用?
判定两直线平行的依据
β
α
γ
a
b
思考3:如果两个相交平面同时和第三个平面相交,那么它们的交线的位置关系如何?
α
β
γ
a
b
l
α
β
γ
a
b
l
平行
相交于一点
思考4:若 ,那么在平面β内经过点P且与l 平行的直线存在吗?有几条?
l
β
α
P
思考5:若平面α、β都与平面γ平行,则平面α与平面β的位置关系如何?
β
α
γ
存在,一条
平行
同平行于一个平面的两个平面平行
理论迁移:
例1 求证:夹在两个平行平面间的平行线段相等.
α
β
D
B
A
C
γ
面面平行的性质定理的几个常用结论:
(1)两个平面平行,其中一个平面内的任意一条直线平行于另一个平面;
(2)夹在两个平行平面之间的平行线段相等;
(3)经过平面外一点有且只有一个平面与已知平面平行;
(4)两条直线被三个平行平面所截,截得的对应线段成比例 ;
(5)如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
例2 在正方体ABCD-A′B′C′D′中,点M在CD′上,试判断直线B′M与平面A′BD的位置关系,并说明理由.
A′
B′
C′
D′
A
B
C
D
M
平行
例3 如图,已知AB、CD是夹在两个平行
平面α、β之间的线段,M、N分别为AB、CD的中点,求证:MN∥平面β.
M
N
A
B
C
D
E
l
β
α
基础强化:
1.已知直线a∥平面α,则a与平面α内的直线的位置关系为( )
A.相交 B.平行 C.异面或平行 D.异面
C
2.已知m?n表示两条直线,α?β?γ表示平面,下列命题中正确的个数是( )
①若α∩γ=m,β∩γ=n,且m∥n,则α∥β;
②若m?n相交且都在α外,m∥α,m∥β,n∥α,
n∥β,则α∥β;
③若m∥α,m∥β,则α∥β;
④若m∥α,n∥β,且m∥n,则α∥β.
A.1 B.2 C.3 D.4
解析:∵直线m与n相交,∴m与n确定一个平面π,
又m∥α,n∥α,∴α∥π,同理β∥π,∴α∥β.故②正确.其它均错.故选A.
A
3.已知平面α∥β,P是α?β外一点,过点P的直线m与α?β分别交于A?C,过点P的直线n与α?β分别交于B?D,且PA=6,AC=9,PD=8,则BD的长为( )
解析:当点P在平面α与β的同侧时,由平行线截线段成比例知
当P在平面α与β之间时,同理可求得BD=24.
B
4.α?β?γ是三个两两平行的平面,且α与β之间的距离是3,α与γ之间的距离是4,则β与γ之间的距离的取值范围是( )
A.{1} B.{7} C.{1,7} D.[1,7]
C
5.已知平面α∥平面β,它们之间的距离为d,直线
a α,则在β内与直线a相距为2d的直线有( )
A.一条 B.两条 C.无数条 D.不存在
B
6.给出下列互不相同的直线l?m?n和平面α?β?γ的三个命题:
①若l与m为异面直线,l α,m β,则α∥β.
②若α∥β,l α,m β,则l∥m.
③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.
其中真命题的个数为( )
A.3 B.2 C.1 D.0
解析:①中α与β也可能相交.∴①错;在②中l与m也可能异面,∴②错.③正确.
C
7.已知直线l∥平面α,设A∈l,B∈l,C∈α,D∈α,且AC∥BD.则AC________BD(填“=”或“≠”).
8.过正方体ABCD—A1B1C1D1的三顶点A1?C1?B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是__________.
=
平行
9.如下图,两条异面直线AC?DF与三个平行平面α?β?γ分别交于A?B?C和D?E?F,又AF?CD分别与β交于G?H,求证:HEGB是平行四边形.
能力提升
证明:∵AC∩CD=C,
∴AC?CD确定平面ACD.
又α∥β,平面ACD与α?β交于AD?BH,∴AD∥BH.又AF∩DF=F,
∴AF?FD确定平面AFD.
又∵α∥β,平面AFD交α?β于AD?GE,∴AD∥GE.∴BH∥GE.
同理BG∥HE.
∴四边形HEGB是平行四边形.
10.如图(1)所示,在空间六边形(即六个顶点中没有任何五点共面)ABCC1D1A1中,每相邻的两边互相垂直,边长均等于a,并且AA1∥CC1.
求证:平面A1BC1∥平面ACD1.
分析:由本题的条件不难联想到正方体,从而用补形法证之.
证明:首先将图形补成正方体框架,如下图(2)所示.
则在正方体ABCD-A1B1C1D1中,证平面A1BC1∥平面ACD1.
由正方体的性质易知,AC∥A1C1.
∴AC∥平面A1BC1,同理
可证CD1∥平面A1BC1.
又AC∩CD1=C,
∴平面A1BC1∥平面ACD1.
11.过平行六面体ABCD—A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有( )
A.4条 B.6条 C.8条 D.12条
解析:如图取各棱的中点.
D
易证平面EFGH∥平面 ,故平行四边形EFGH的四条边及对角线均为各棱中点的连线均平行于面 ,共6条,同理在平行四边形JKMN中也有6条满足条件,故共有12条.
12.如图,在四面体ABCD中,CB=CD,AD⊥BD,且E?F分别是AB?BD的中点.
求证:直线EF∥面ACD.
证明:在△ABD中,
∵E?F分别是AB?BD的中点,
∴EF∥AD.
又AD 平面ACD,
EF 平面ACD,
∴直线EF∥面ACD.
题型一 证明线面平行
例1.在正方体ABCD-A1B1C1D1中,E为CD的中点,F为B1C1的中点.
求证:EF∥平面BB1D1D.
分析:如右图所示.
要证线面平行,可先证面面平行,取BC的中点H,连结FH?EH.
易证平面EFH∥平面 .
再用两面平行的性质得证.
证明:如上图,取BC的中点H.连结EH,FH.∵E为CD的中点.
∴EH∥BD,EH 平面 .∴EH∥平面 .
又F为 的中点.∴ BH,∴ 为平行四边形,
∴FH∥ ,又FH 平面 .∴FH∥平面 .
又FH∩EH=H,∴平面EFH∥平面 .
∴EF∥平面 .
规律技巧:在证明线面平行时,常用:线线平行,线面平行,面面平行进行相互转化,达到证题的目的.
变式训练1:如图所示,直三棱柱ABC—A1B1C1底面为等腰直角三角形,∠ABC=90°, P?Q分别为A1B和CC1的中点。求证:PQ∥平面A1B1C1.
证法一:如图(1)所示,取A1B1的中点D,连结DP?DC1,则有DP? .
又Q为CC1的中点,
∴DP? QC1.
∴四边形PQC1D是平行四边形,
∴PQ∥C1D.
又PQ 平面A1B1C1,
C1D 平面A1B1C1,
∴PQ∥平面A1B1C1.
证法二:如图(2)所示,取BB1的中点E,连结EP?EQ,则有PE∥A1B1,QE∥B1C1.
又PE 平面A1B1C1,QE 平面A1B1C1,A1B1 平面A1B1C1,B1C1 平面A1B1C1,
∴PE∥平面A1B1C1,QE∥平面A1B1C1.
又PE 平面PQE,QE 平面PQE,PE∩QE=E,
∴平面PQE∥平面A1B1C1.
又PQ 平面PQE,
∴PQ∥平面A1B1C1.
题型二 证明面面平行
例2.已知a,b是异面直线,a 平面α,b 平面β,a∥β,b∥α,求证:α∥β.
分析:要证α∥β,由判定定理知,在β内找出两
条相交直线都平行于α.由已知,b β,b∥α,
再找出一条直线a′∥α.这需要作辅助平面γ,
使γ∩α=a,γ∩β=a′,只要a′∥a,就可得
α∥β,具体如何作出辅助平面γ,请看证明.
证明:在b上任取一点P,设直线a与点P确定平面为γ,如下图所示.
设β∩γ=a′,∵a∥β,∴a′∥a,∴a′∥α.
又b∥α,且a′∩b=P,a′ β,b β,
∴α∥β.
变式训练2.已知:平面α∥平面β,平面β∥平面γ.
求证:α∥γ.
证明:如图,作两个相交平面分别与α?β?γ交于a?c?e
和b?d?f.
∵α∥β,
∴a∥c,b∥d.
又β∥γ,∴c∥e,d∥f.
∴a∥e,b∥f,又a与b相交,
∴α∥γ.
题型三 综合性问题
例3.如下图,在三棱柱ABC—A1B1C1中,点D?D1分别为AC?A1C1上的点.
(1)当 的值等于何值时,
BC1∥平面AB1D1;
(2)若平面BC1D∥平面AB1D1,
求 的值.
分析:若BC1∥平面AB1D1,则平面AB1D1中存在直线与BC1平行,连结A1B交AB1于O,由棱柱的定义知O为A1B的中点,平面A1BC1与平面AB1D1的交线OD1与直线BC1平行,由
三角形中位线定理知D1为
A1C1的中点,此时
若平面BC1D∥平面AB1D1,
易知
解:(1)如下图,取D1为线段A1C1的中点,此时
连结A1B交AB1于点O,连结OD1.
由棱柱的定义,知四边形A1ABB1为平行四边形,所以点O为A1B的中点.
在△A1BC1中,点O?D1分别为A1B?A1C1的中点,∴OD1∥BC1.
又∵OD1 平面AB1D1,BC1 平面AB1D1,
∴BC1∥平面AB1D1.
∴ 时,BC1∥平面AB1D1.
(2)由已知,平面BC1D∥平面AB1D1.
且平面A1BC1∩平面BDC1=BC1,
平面A1BC1∩平面AB1D1=D1O,
因此BC1∥D1O,同理AD1∥DC1.
规律技巧:探索平行问题,即找平行成立具备的条件,
三种平行关系的相互转化是解决问题常用的方法.
变式训练3.如图,已知α∥β,P是平面α,β外的一点,直线PAB,PCD分别与α?β相交于A?B和C?D.
(1)求证:AC∥BD;
(2)已知PA=4,AB=5,PC=3,求PD的长.
(1)证明:∵PB∩PD=P,∴直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD,又α∥β,∴AC∥BD.
(2)解:由(1)得AC∥BD,
作业:
P61练习:(做在书上)
P63习题2.2B组:4(做在书上)
P63习题2.2B组:3.
