高中数学人教A版必修三:2.2.1 用样本的频率分布估计总体分布 课件(24张PPT)
文档属性
| 名称 | 高中数学人教A版必修三:2.2.1 用样本的频率分布估计总体分布 课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:33:53 | ||
图片预览





文档简介
2.2.1 用样本的频率分布估计总体分布
统计的基本思想方法
用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况.
统计的核心问题
如何根据样本的情况对总体的情况作出推断.这里包括两类问题:
一类是如何从总体中抽取样本?(已学习)
另一类是如何根据对样本的整理、计算、分析, 对总体的情况作出推断.
用样本的有关情况去估计总体的相应情况,
大体分为两类:
一类是用样本频率分布估计总体分布;
一类是用样本的某种数字特征(例如平均数、方差等)去估计总体的相应数字特征。
整体介绍
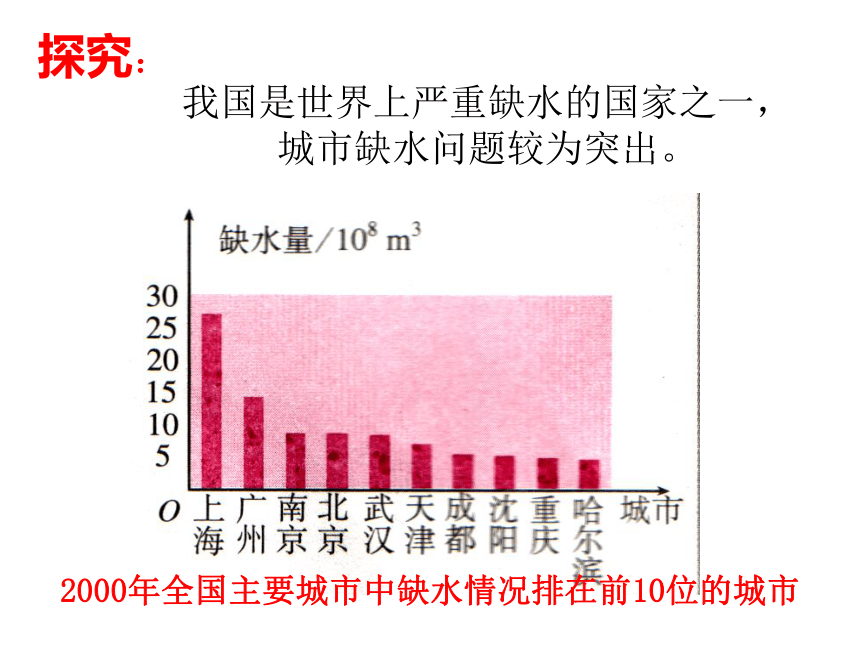
我国是世界上严重缺水的国家之一,
城市缺水问题较为突出。
2000年全国主要城市中缺水情况排在前10位的城市
探究:
问题:某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费。
①如果希望大部分居民的日常生活不受影响,那
么标准a定为多少比较合理呢?
②为了较合理地确定这个标准,你认为需要做
哪些工作?
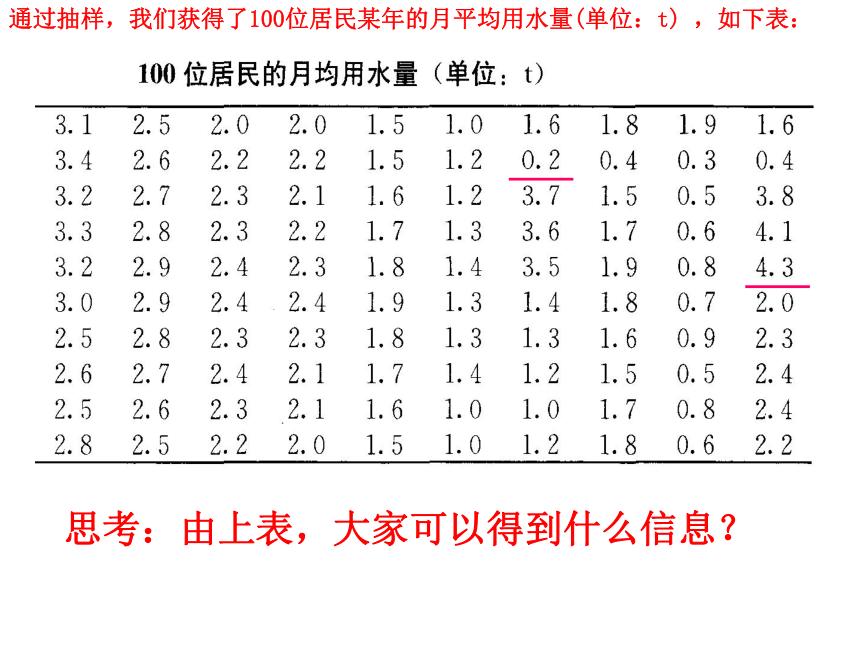
思考:由上表,大家可以得到什么信息?
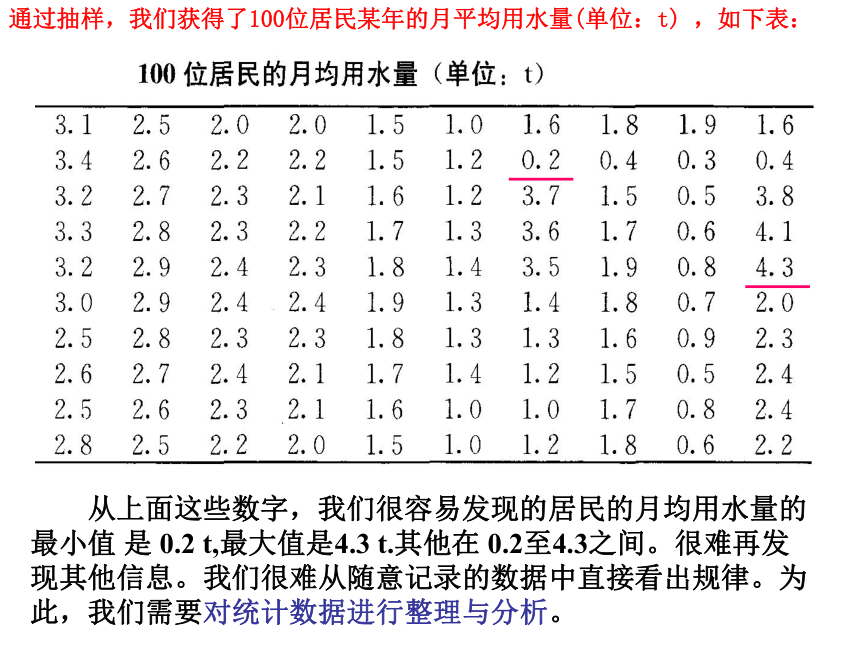
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
从上面这些数字,我们很容易发现的居民的月均用水量的最小值 是 0.2 t,最大值是4.3 t.其他在 0.2至4.3之间。很难再发现其他信息。我们很难从随意记录的数据中直接看出规律。为此,我们需要对统计数据进行整理与分析。
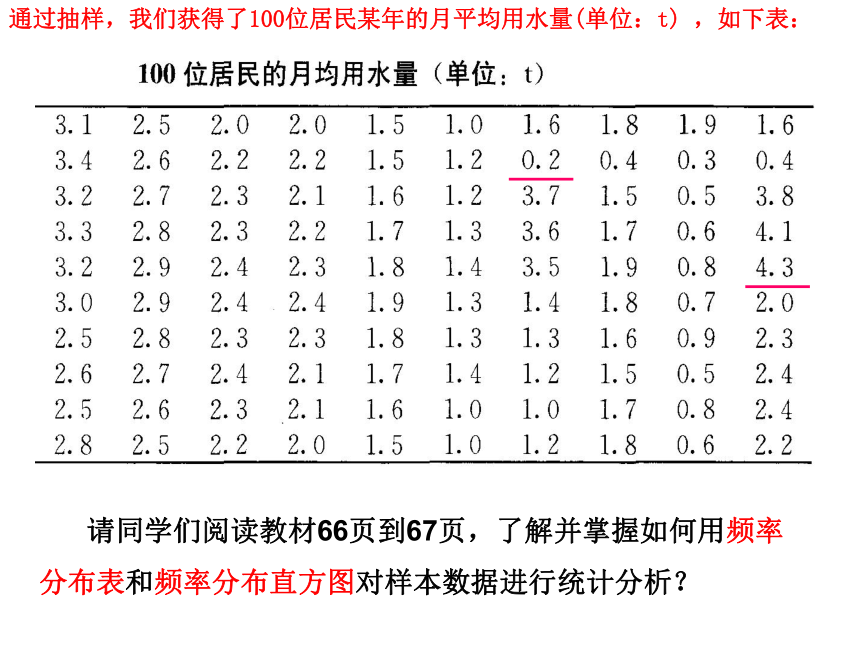
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
请同学们阅读教材66页到67页,了解并掌握如何用频率
分布表和频率分布直方图对样本数据进行统计分析?
画频率分布直方图的操作步骤
(一表一图的制作方法)
1.求极差.即数据中最大值与最小值的差
2.决定组距与组数 :组数=极差/组距
3.将数据分组.通常对组内数值所在区间,取左闭右开区间 , 最后一组取闭区间
4.列出频率分布表.计算频数和频率, 列出频率分布表
5.画出频率分布直方图(纵轴表示频率/组距)
100位居民月平均用水量的频率分布表
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
100位居民月平均用水量的频率分布直方图
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
小长方形的面积=?
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
小长方形的面积总和=?
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
月均用水量最多的在哪个区间?
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
请大家阅读第68页,直方图有那些优点和缺点?
画频率分布直方图的操作步骤
1.画平面直角坐标系
2.在横轴上均匀标出各组分点,在纵轴上标出单位长度
3.以组距为宽,各组的频率与组距的商为高,分别画出各组对应的小长方形
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图
利用样本频分布对总体分布进行相应估计
(2)当样本容量无限增大(无限大时即认为达到总体时),作图时所分的组数增加,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线—总体密度曲线。
(1)样本容量越大,这种估计越精确。
问题:上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?
总体密度曲线
频率
组距
月均用水量/t
a
b
图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比(频率)。
频率
组距
月均用水量/t
a
b
图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比(频率)。
总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具。
练 习
有一个容量为50的样本数据的分组的频数如下:
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5] 4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;并在频率分布直方图中画出频率分布折线图;
(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少?
课堂练习:
2、为检测某种产品的质量,抽取了一个容量为30的样本,检测结果为一级品5件,二级品8件,三级品13件,次品4件.
(1) 列出样本的频率分布表;
(2)根据上述结果,估计此种产品为二级品或三级品的概率约是多少.
解:
(1)样本的频率分布
表为:
0.13
4
次品
0.43
13
三级品
0.27
8
二级品
0.17
5
一级品
频率
频数
产品
(2)此种产品为二级品或三级品的概率约为0.27+0.43=0.7.
3.一个容量为100的样本,数据的分组和各组的相关信息如下表,试完成表中每一行的两个空格.
分组
频数
频率
频率累计
[12,15)
6
[15,18)
0.08
[18,21)
0.30
[21,24)
21
[24,27)
0.69
[27,30)
16
[30,33)
0.10
[33,36]
1.00
合计
100
1.00
小结:
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
注意
(2)纵坐标为:
统计的基本思想方法
用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况.
统计的核心问题
如何根据样本的情况对总体的情况作出推断.这里包括两类问题:
一类是如何从总体中抽取样本?(已学习)
另一类是如何根据对样本的整理、计算、分析, 对总体的情况作出推断.
用样本的有关情况去估计总体的相应情况,
大体分为两类:
一类是用样本频率分布估计总体分布;
一类是用样本的某种数字特征(例如平均数、方差等)去估计总体的相应数字特征。
整体介绍
我国是世界上严重缺水的国家之一,
城市缺水问题较为突出。
2000年全国主要城市中缺水情况排在前10位的城市
探究:
问题:某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a , 用水量不超过a的部分按平价收费,超过a的部分按议价收费。
①如果希望大部分居民的日常生活不受影响,那
么标准a定为多少比较合理呢?
②为了较合理地确定这个标准,你认为需要做
哪些工作?
思考:由上表,大家可以得到什么信息?
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
从上面这些数字,我们很容易发现的居民的月均用水量的最小值 是 0.2 t,最大值是4.3 t.其他在 0.2至4.3之间。很难再发现其他信息。我们很难从随意记录的数据中直接看出规律。为此,我们需要对统计数据进行整理与分析。
通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表:
请同学们阅读教材66页到67页,了解并掌握如何用频率
分布表和频率分布直方图对样本数据进行统计分析?
画频率分布直方图的操作步骤
(一表一图的制作方法)
1.求极差.即数据中最大值与最小值的差
2.决定组距与组数 :组数=极差/组距
3.将数据分组.通常对组内数值所在区间,取左闭右开区间 , 最后一组取闭区间
4.列出频率分布表.计算频数和频率, 列出频率分布表
5.画出频率分布直方图(纵轴表示频率/组距)
100位居民月平均用水量的频率分布表
频率/组距
月平均用水量/t
0.50
0.40
0.30
0.20
0.10
0
0.5 1 1.5 2 2.5 3 3.5 4 4.5
100位居民月平均用水量的频率分布直方图
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
小长方形的面积=?
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
小长方形的面积总和=?
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
月均用水量最多的在哪个区间?
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
请大家阅读第68页,直方图有那些优点和缺点?
画频率分布直方图的操作步骤
1.画平面直角坐标系
2.在横轴上均匀标出各组分点,在纵轴上标出单位长度
3.以组距为宽,各组的频率与组距的商为高,分别画出各组对应的小长方形
频率分布直方图如下:
月均用水量/t
频率
组距
0.10
0.20
0.30
0.40
0.50
0.5
1
1.5
2
2.5
3
3.5
4
4.5
连接频率分布直方图中各小长方形上端的中点,得到频率分布折线图
利用样本频分布对总体分布进行相应估计
(2)当样本容量无限增大(无限大时即认为达到总体时),作图时所分的组数增加,组距无限缩小,那么频率分布折线图就会无限接近于一条光滑曲线—总体密度曲线。
(1)样本容量越大,这种估计越精确。
问题:上例的样本容量为100,如果增至1000,其频率分布直方图的情况会有什么变化?假如增至10000呢?
总体密度曲线
频率
组距
月均用水量/t
a
b
图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比(频率)。
频率
组距
月均用水量/t
a
b
图中阴影部分的面积,表示总体在某个区间 (a, b) 内取值的百分比(频率)。
总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具。
练 习
有一个容量为50的样本数据的分组的频数如下:
[12.5, 15.5) 3
[15.5, 18.5) 8
[18.5, 21.5) 9
[21.5, 24.5) 11
[24.5, 27.5) 10
[27.5, 30.5) 5
[30.5, 33.5] 4
(1)列出样本的频率分布表;
(2)画出频率分布直方图;并在频率分布直方图中画出频率分布折线图;
(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少?
课堂练习:
2、为检测某种产品的质量,抽取了一个容量为30的样本,检测结果为一级品5件,二级品8件,三级品13件,次品4件.
(1) 列出样本的频率分布表;
(2)根据上述结果,估计此种产品为二级品或三级品的概率约是多少.
解:
(1)样本的频率分布
表为:
0.13
4
次品
0.43
13
三级品
0.27
8
二级品
0.17
5
一级品
频率
频数
产品
(2)此种产品为二级品或三级品的概率约为0.27+0.43=0.7.
3.一个容量为100的样本,数据的分组和各组的相关信息如下表,试完成表中每一行的两个空格.
分组
频数
频率
频率累计
[12,15)
6
[15,18)
0.08
[18,21)
0.30
[21,24)
21
[24,27)
0.69
[27,30)
16
[30,33)
0.10
[33,36]
1.00
合计
100
1.00
小结:
频率分布直方图
应用
步骤
1.求极差
2.决定组距与组数
3.将数据分组
4.列频率分布表
5.画频率分布直方图
注意
(2)纵坐标为:
