高中数学人教A版必修一:2.1.2 指数函数及其性质 课件(19张PPT)
文档属性
| 名称 | 高中数学人教A版必修一:2.1.2 指数函数及其性质 课件(19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 661.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:36:32 | ||
图片预览




文档简介
2.1.2指数函数
及其性质
问题1、
一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是:
新课导入
木棰
剩余
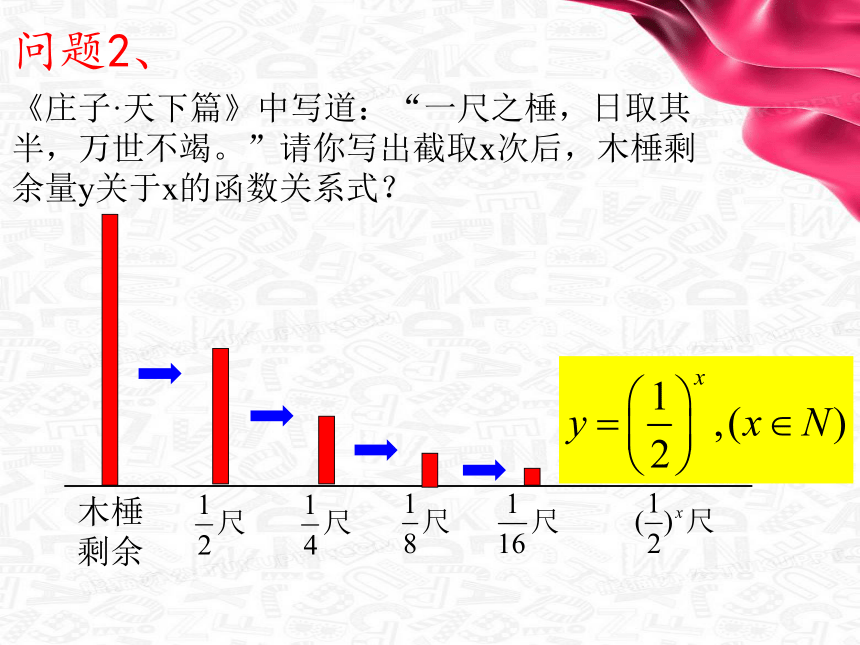
问题2、
《庄子·天下篇》中写道:“一尺之棰,日取其 半,万世不竭。”请你写出截取x次后,木棰剩余量y关于x的函数关系式?
整体只有一项
自变量在指数的位置上
系数为1
y= ax
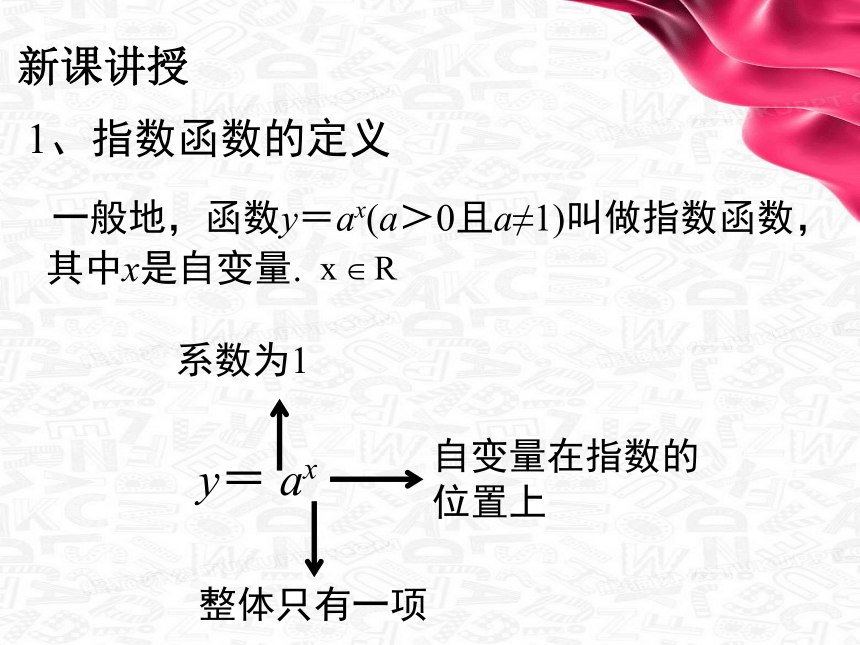
1、指数函数的定义
一般地,函数y=ax(a>0且a≠1)叫做指数函数,
其中x是自变量.
新课讲授
1.下列函数是指数函数的是
概念辨析
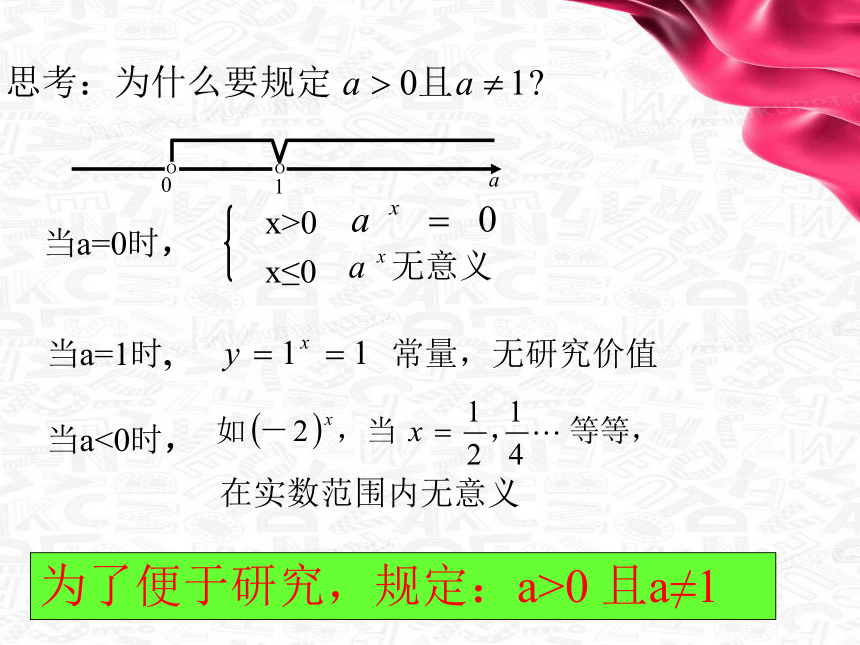
当a=1时,
当a=0时,
当a<0时,
x≤0
x>0
为了便于研究,规定:a>0 且a≠1
?
?
0
1
a
常量,无研究价值
在实数范围内无意义
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
概念辨析
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
x
0
1
2
3
…
1
2
4
8
…
-1
-2
-3
…
…
-0.5
0.5
…
0.71
1.4
…
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
认识
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
恒 过 点:
在 R 上是单调
在 R 上是单调
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
2、指数函数的图像及性质
奇偶性:非奇非偶函数
解:将点 ,代入 得到
即 ,解得: ,于是 ,
所以,
例1:已知指数函数 的图象
过点 ,
例2 比较下面两个值的大小
因为1.7>1,所以函数y=
<
解(1):构造指数函数
在R上是增函数,而2.5<3,
所以,
1.函数y=2-x的大致图象是 ( )
答案:B
2.已知集合M={y∈R|y=2x,x>0},N={x∈R|x2-2x<0},则M∩N=( )
A.(1,2) B.(1,+∞)
C.[2,+∞) D.(-∞,0]∪(1,+∞)
答案:A
巩固练习
3.已知2x>21-x,则x的取值范围是( )
答案:C
4.若a>3,则函数f(x)=4(a-2)2x+6-1的图象恒过定点的坐标是 .?
解析:∵a>3,∴a-2>1.令2x+6=0,得x=-3,
则f(-3)=4(a-2)0-1=3.
故函数f(x)的图象恒过定点的坐标是(-3,3).
答案:(-3,3)
课 堂 小 结
作 业 布 置
课本59页5、7、8
结 束 语
数学告诉你,只要你每天坚持比别人努力一点点,你的人生将大不相同
及其性质
问题1、
一张白纸对折一次得两层,对折两次得4层,对折3次得8层,问若对折 x 次所得层数为y,则y与x 的函数关系是:
新课导入
木棰
剩余
问题2、
《庄子·天下篇》中写道:“一尺之棰,日取其 半,万世不竭。”请你写出截取x次后,木棰剩余量y关于x的函数关系式?
整体只有一项
自变量在指数的位置上
系数为1
y= ax
1、指数函数的定义
一般地,函数y=ax(a>0且a≠1)叫做指数函数,
其中x是自变量.
新课讲授
1.下列函数是指数函数的是
概念辨析
当a=1时,
当a=0时,
当a<0时,
x≤0
x>0
为了便于研究,规定:a>0 且a≠1
?
?
0
1
a
常量,无研究价值
在实数范围内无意义
2.函数 y = ( a2 - 3a + 3) ax 是指数函数,求 a的值.
解:由指数函数 的定义有
a2 - 3a + 3=1
a>0
a ≠ 1
∴ a = 2
a =1或a = 2
a>0
a≠1
解得
概念辨析
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
x
0
1
2
3
…
1
2
4
8
…
-1
-2
-3
…
…
-0.5
0.5
…
0.71
1.4
…
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
8
7
6
5
4
3
2
1
-6
-4
-2
2
4
6
认识
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
恒 过 点:
在 R 上是单调
在 R 上是单调
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
2、指数函数的图像及性质
奇偶性:非奇非偶函数
解:将点 ,代入 得到
即 ,解得: ,于是 ,
所以,
例1:已知指数函数 的图象
过点 ,
例2 比较下面两个值的大小
因为1.7>1,所以函数y=
<
解(1):构造指数函数
在R上是增函数,而2.5<3,
所以,
1.函数y=2-x的大致图象是 ( )
答案:B
2.已知集合M={y∈R|y=2x,x>0},N={x∈R|x2-2x<0},则M∩N=( )
A.(1,2) B.(1,+∞)
C.[2,+∞) D.(-∞,0]∪(1,+∞)
答案:A
巩固练习
3.已知2x>21-x,则x的取值范围是( )
答案:C
4.若a>3,则函数f(x)=4(a-2)2x+6-1的图象恒过定点的坐标是 .?
解析:∵a>3,∴a-2>1.令2x+6=0,得x=-3,
则f(-3)=4(a-2)0-1=3.
故函数f(x)的图象恒过定点的坐标是(-3,3).
答案:(-3,3)
课 堂 小 结
作 业 布 置
课本59页5、7、8
结 束 语
数学告诉你,只要你每天坚持比别人努力一点点,你的人生将大不相同
