人教A版高中数学必修1第三章3.1.2 用二分法求方程的近似解课件(20张PPT)
文档属性
| 名称 | 人教A版高中数学必修1第三章3.1.2 用二分法求方程的近似解课件(20张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 427.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 15:41:24 | ||
图片预览








文档简介
用二分法求方程的近似解
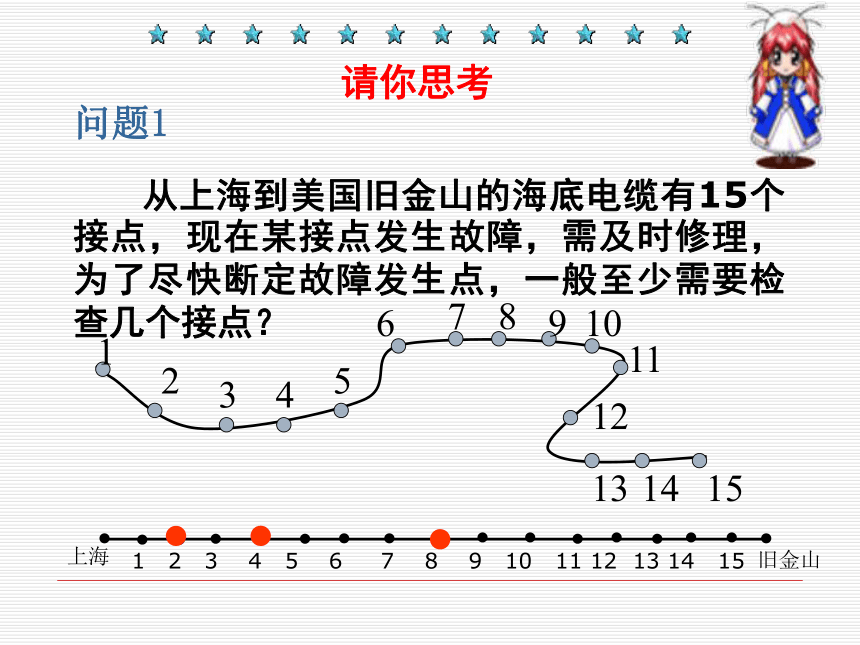
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
请你思考
问题1
上海
旧金山
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
有16个大小相同的小球,其
中有15个小球质量相等,另有一个
小球较重,用天平称几次就可以找
出这个较重的球?(要求测量次数
尽可能少。)
问题2
4次
请你思考
知识探究(一)
数学来源于生活,生活中处处有数学!
通过刚才的游戏和生活中我们对实际问题的处理,同学们,你们找到了处理这类问题的一般性规律吗?
每次取中点,将区间一分为二,再经比较,按需要留下其中一个小区间,直至完成要求。
这种方法在查找线路,如电线、水管、气管等管道线路故障时经常用到。
它们都用到数学中二分法的思想,这种方法也是求方程的近似解常用的方法!
知识探究(一)
上节课我们学了什么定理?它的作用是什么?还有什么问题没有解决?
知识探究(二)
使f(x)=0的实数x叫做函数y=f(x)的零点。
复习回顾 :
1、函数的零点的定义:
2、零点存在性判定法则
已知函数 在区
间(2,3)内存在一个零点。
3、例题处理
如何求出方程
在(2,3)的近似解(精确度为0.01)?
怎样计算函数 在区间(2,3)内精确度为0.01的零点近似值?
区间(a,b)
中点值m
f(m)的近似值
精确度|a-b|
(2,3)
2.5
-0.084
1
(2.5,3)
2.75
0.512
0.5
(2.5,2.75)
2.625
0.215
0.25
(2.5,2.625)
2.562 5
0.066
0.125
(2.5,2.562 5)
2.531 25
-0.009
0.0625
(2.531 25,2.562 5)
2.546 875
0.029
0.03125
(2.531 25,2.546 875)
2.539 062 5
0.01
0.015625
(2.531 25,2.539 062 5)
2.535 156 25
0.001
0.007813
对于在区间[a,b]上连续不断,且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两端点逐步逼近零点,进而得到零点(或对应方程的根)近似值的方法叫做二分法.
问题1.如何描述二分法?
知识探究(三)
问题2:二分法实质是什么?
用二分法求方程的近似解,实质上就是通过“取中点”的方法,运用“逼近”思想逐步缩小零点所在的区间。
问题3:能否给出二分法求解方程f(x)=0(或
g(x)=h(x))近似解的基本步骤?
1、求函数f(x)的零点近似值第一步:确定区
间[a,b],使 f(a)f(b)<0;
2、为了缩小零点所在区间的范围,接下来应做:
求区间的中点c,并计算f(c)的值
3、若f(c)=0说明什么?若f(a)·f(c)<0
或f(c)·f(b)<0 ,则分别说明什么?
若f(c)=0 ,则c就是函数的零点;
若f(a)·f(c)<0 ,则零点x0∈(a,c);
若f(c)·f(b)<0 ,则零点x0∈(c,b).
问题4:若给定精确度ε,如何选取近似值?
当|m—n|<ε时,区间[m,n]内的任
意一个值都是函数零点的近似值。
练习1:
能否求解以下方程(精确度为0.1)
x3+3x-1=0
实战演练:
解:令f(x)=x3+3x-1, 有f(0)<0,f(1)>0,则方 程的解在 0,1之间。(精确度为0.1)
根所在区间
区间端点函数值符号
中点值
中点函数值符号
(0,1)
f(0)<0,f(1)>0
0.5
f(0.5)>0
(0,0.5)
(0.25,0.5)
(0.25,0.375)
(0.25,0.3125)
f(0)<0,f(0.5)>0
f(0.25)<0,f(0.5)>0
f(0.25)<0,f(0.375)>0
0.25
f(0.25)<0
0.375
f(0.375)>0
0.3125
f(0.3125)<0
练习2:
下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )
C
x
y
0
x
y
0
x
y
0
x
y
0
问题5:根据练习2,请思考利用二分法求函数
零点的条件是什么?
1. 函数y=f (x)在[a,b]上连续不断.
2. y=f (x)满足 f (a) ·f (b)<0,则在(a,b)内必有零点.
今天你学到
了什么?
?
?
?
谢谢大家,
请批评指正!
因为有你们,
今天很快乐!
再 见
从上海到美国旧金山的海底电缆有15个接点,现在某接点发生故障,需及时修理,为了尽快断定故障发生点,一般至少需要检查几个接点?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
请你思考
问题1
上海
旧金山
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
有16个大小相同的小球,其
中有15个小球质量相等,另有一个
小球较重,用天平称几次就可以找
出这个较重的球?(要求测量次数
尽可能少。)
问题2
4次
请你思考
知识探究(一)
数学来源于生活,生活中处处有数学!
通过刚才的游戏和生活中我们对实际问题的处理,同学们,你们找到了处理这类问题的一般性规律吗?
每次取中点,将区间一分为二,再经比较,按需要留下其中一个小区间,直至完成要求。
这种方法在查找线路,如电线、水管、气管等管道线路故障时经常用到。
它们都用到数学中二分法的思想,这种方法也是求方程的近似解常用的方法!
知识探究(一)
上节课我们学了什么定理?它的作用是什么?还有什么问题没有解决?
知识探究(二)
使f(x)=0的实数x叫做函数y=f(x)的零点。
复习回顾 :
1、函数的零点的定义:
2、零点存在性判定法则
已知函数 在区
间(2,3)内存在一个零点。
3、例题处理
如何求出方程
在(2,3)的近似解(精确度为0.01)?
怎样计算函数 在区间(2,3)内精确度为0.01的零点近似值?
区间(a,b)
中点值m
f(m)的近似值
精确度|a-b|
(2,3)
2.5
-0.084
1
(2.5,3)
2.75
0.512
0.5
(2.5,2.75)
2.625
0.215
0.25
(2.5,2.625)
2.562 5
0.066
0.125
(2.5,2.562 5)
2.531 25
-0.009
0.0625
(2.531 25,2.562 5)
2.546 875
0.029
0.03125
(2.531 25,2.546 875)
2.539 062 5
0.01
0.015625
(2.531 25,2.539 062 5)
2.535 156 25
0.001
0.007813
对于在区间[a,b]上连续不断,且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两端点逐步逼近零点,进而得到零点(或对应方程的根)近似值的方法叫做二分法.
问题1.如何描述二分法?
知识探究(三)
问题2:二分法实质是什么?
用二分法求方程的近似解,实质上就是通过“取中点”的方法,运用“逼近”思想逐步缩小零点所在的区间。
问题3:能否给出二分法求解方程f(x)=0(或
g(x)=h(x))近似解的基本步骤?
1、求函数f(x)的零点近似值第一步:确定区
间[a,b],使 f(a)f(b)<0;
2、为了缩小零点所在区间的范围,接下来应做:
求区间的中点c,并计算f(c)的值
3、若f(c)=0说明什么?若f(a)·f(c)<0
或f(c)·f(b)<0 ,则分别说明什么?
若f(c)=0 ,则c就是函数的零点;
若f(a)·f(c)<0 ,则零点x0∈(a,c);
若f(c)·f(b)<0 ,则零点x0∈(c,b).
问题4:若给定精确度ε,如何选取近似值?
当|m—n|<ε时,区间[m,n]内的任
意一个值都是函数零点的近似值。
练习1:
能否求解以下方程(精确度为0.1)
x3+3x-1=0
实战演练:
解:令f(x)=x3+3x-1, 有f(0)<0,f(1)>0,则方 程的解在 0,1之间。(精确度为0.1)
根所在区间
区间端点函数值符号
中点值
中点函数值符号
(0,1)
f(0)<0,f(1)>0
0.5
f(0.5)>0
(0,0.5)
(0.25,0.5)
(0.25,0.375)
(0.25,0.3125)
f(0)<0,f(0.5)>0
f(0.25)<0,f(0.5)>0
f(0.25)<0,f(0.375)>0
0.25
f(0.25)<0
0.375
f(0.375)>0
0.3125
f(0.3125)<0
练习2:
下列函数的图象与x轴均有交点,其中不能用二分法求其零点的是 ( )
C
x
y
0
x
y
0
x
y
0
x
y
0
问题5:根据练习2,请思考利用二分法求函数
零点的条件是什么?
1. 函数y=f (x)在[a,b]上连续不断.
2. y=f (x)满足 f (a) ·f (b)<0,则在(a,b)内必有零点.
今天你学到
了什么?
?
?
?
谢谢大家,
请批评指正!
因为有你们,
今天很快乐!
再 见
