人教A版高中数学必修四第二章:2.2.1 向量加法运算及其几何意义 课件(14张PPT)
文档属性
| 名称 | 人教A版高中数学必修四第二章:2.2.1 向量加法运算及其几何意义 课件(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览


文档简介
2.2.1 向量加法运算及其几何意义
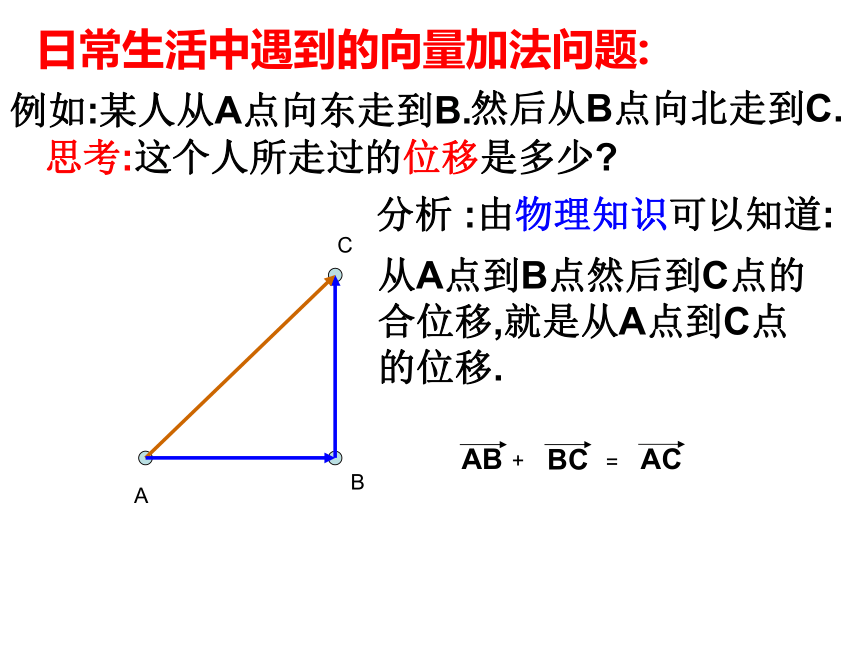
例如:某人从A点向东走到B.
日常生活中遇到的向量加法问题:
然后从B点向北走到C.
思考:这个人所走过的位移是多少?
A
B
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的
合位移,就是从A点到C点
的位移.
AB
BC
AC
=
+
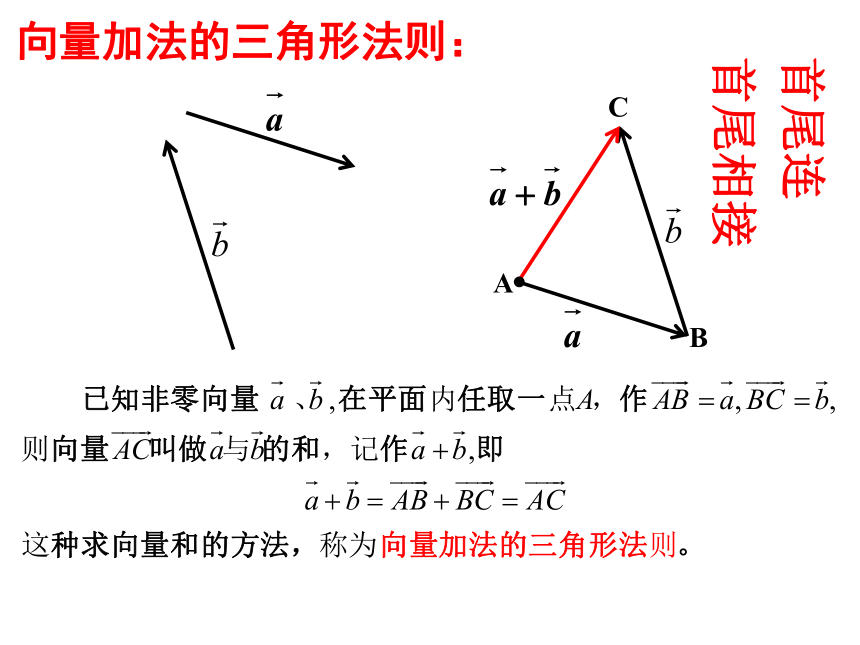
向量加法的定义:我们把求两个向量 的和的运算,叫做向量的加法, 叫做 的和向量.
思考:任意给出两个向量 ,
如何求 ?
向量加法的三角形法则:
C
A
B
首尾连
首尾相接
O
A
B
C
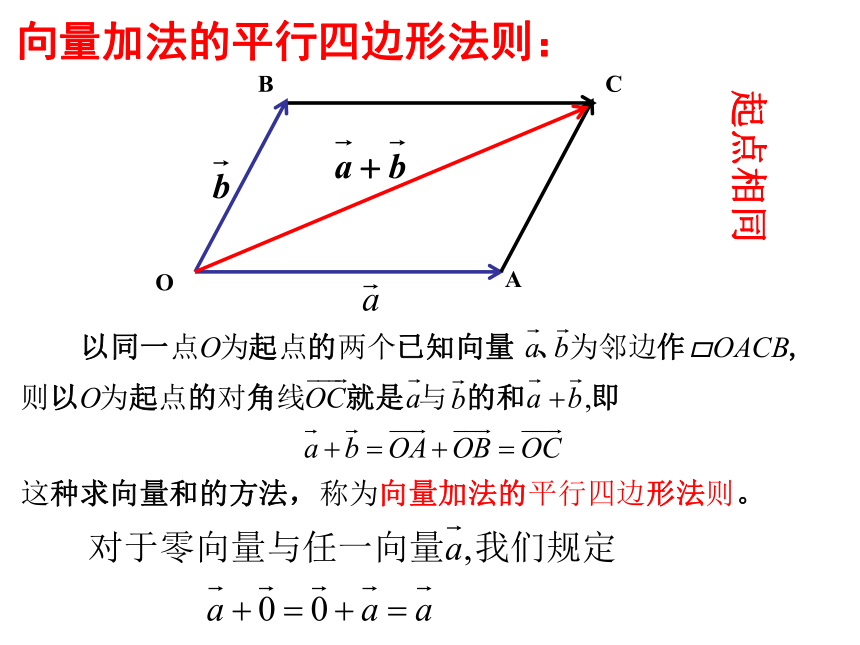
起点相同
向量加法的平行四边形法则:
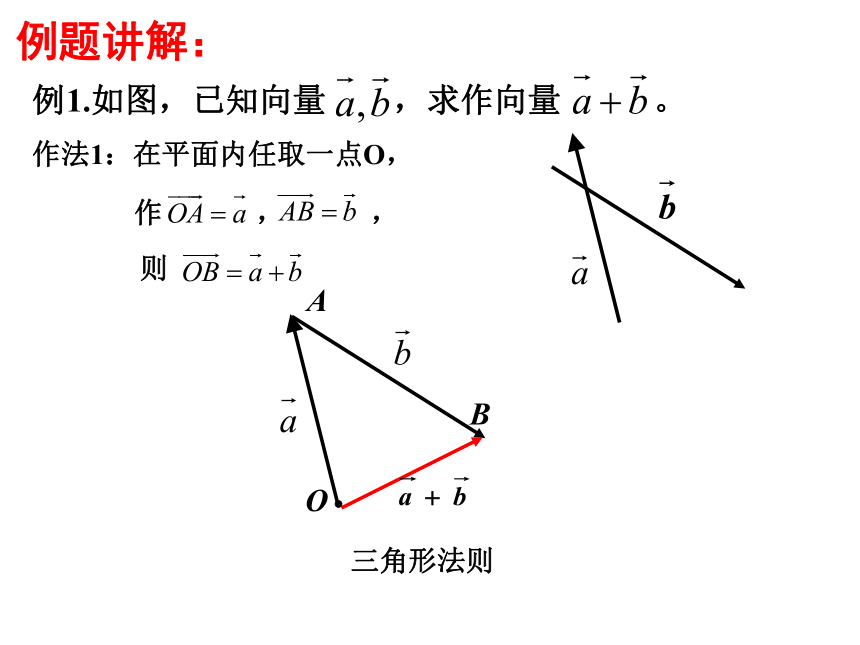
例1.如图,已知向量 ,求作向量 。
则
三角形法则
作法1:在平面内任取一点O,
作 , ,
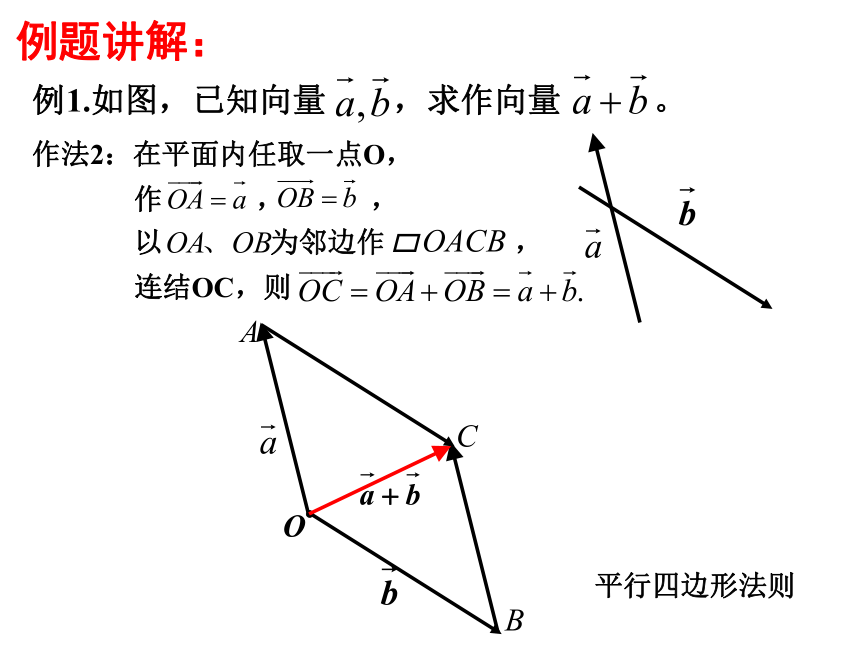
例题讲解:
例1.如图,已知向量 ,求作向量 。
例题讲解:
作法2:在平面内任取一点O,
作 , ,
以 为邻边作 ,
连结OC,则
平行四边形法则
探究:如图,当在数轴上表示两个共线向量时,它们的加法和
数的加法有什么关系?
(1)
(2)
A
B
C
B
C
A
因此,
思考:
例2:
A
B
C
D
E
根据图示填空:
练习:
P84 第1—4题
1、(1)
(2)
书本84页课堂练习
2、(1)
(2)
作业布置:
P91 A组 第 2题
第4(1)(2)(3)题
1、向量加法的三角形法则(首尾相接,首尾连)
课堂小结:
2、向量加法的平行四边形法则(起点相同)
3、向量加法的交换律与结合律。
例如:某人从A点向东走到B.
日常生活中遇到的向量加法问题:
然后从B点向北走到C.
思考:这个人所走过的位移是多少?
A
B
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的
合位移,就是从A点到C点
的位移.
AB
BC
AC
=
+
向量加法的定义:我们把求两个向量 的和的运算,叫做向量的加法, 叫做 的和向量.
思考:任意给出两个向量 ,
如何求 ?
向量加法的三角形法则:
C
A
B
首尾连
首尾相接
O
A
B
C
起点相同
向量加法的平行四边形法则:
例1.如图,已知向量 ,求作向量 。
则
三角形法则
作法1:在平面内任取一点O,
作 , ,
例题讲解:
例1.如图,已知向量 ,求作向量 。
例题讲解:
作法2:在平面内任取一点O,
作 , ,
以 为邻边作 ,
连结OC,则
平行四边形法则
探究:如图,当在数轴上表示两个共线向量时,它们的加法和
数的加法有什么关系?
(1)
(2)
A
B
C
B
C
A
因此,
思考:
例2:
A
B
C
D
E
根据图示填空:
练习:
P84 第1—4题
1、(1)
(2)
书本84页课堂练习
2、(1)
(2)
作业布置:
P91 A组 第 2题
第4(1)(2)(3)题
1、向量加法的三角形法则(首尾相接,首尾连)
课堂小结:
2、向量加法的平行四边形法则(起点相同)
3、向量加法的交换律与结合律。
