人教A版高中数学选修2-1:1.2充分条件与必要条件课件(22张PPT)
文档属性
| 名称 | 人教A版高中数学选修2-1:1.2充分条件与必要条件课件(22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 582.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 17:07:05 | ||
图片预览








文档简介
(共22张PPT)
§1.2
充分条件与必要条件
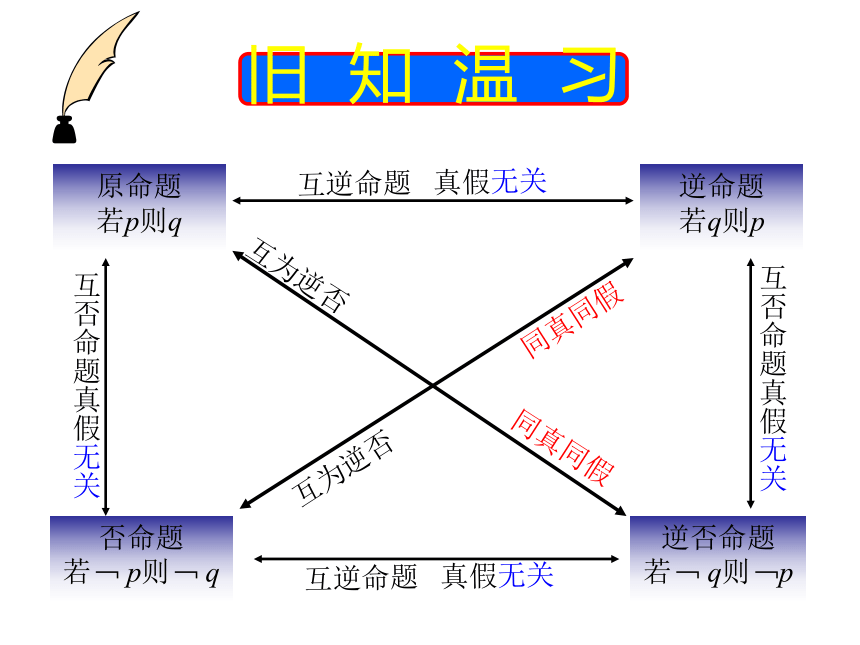
旧知温习
原命题
若p则q
逆命题
若q则p
否命题
若﹁
p则﹁
q
逆否命题
若﹁
q则﹁p
互为逆否
同真同假
互为逆否
同真同假
互逆命题
真假无关
互逆命题
真假无关
互否命题真假无关
互否命题真假无关
符号
与
的介绍
如果命题为真,即如果p成立,那么q一定成立,
记作
,读作
“
p推出
q
”.
p
q
如果命题为假,即如果p成立,那么q不成立,
记作
,读作
“
p推不出
q
”.
p
q
现有命题“若p则q”,
新知准备
定义:如果命题“若p,则q”为真命题,即p
?
q,
那么我们就说p是q的充分条件;q是p的必要条件.
【定义得出】
①充分性:条件是充分的,也就是说条件是充足的,足够的,足以保证的。符合“若p则q”为真(p=>q)的形式,即“有之必成立”。
②必要性:必要就是必须的,必不可少的。符合“若非q则非p”
为真(非q=>非p)的形式,即“无之必不成立”。
注:
③p是q的充分条件与q是p的必要条件是完全等价的,它们是同一个逻辑关系“p=>q”的不同表达方法。
问题
?
1
2
3
4
5
6
7
x
>0
x
=
√2
两三角形全等
a、b为奇数
ab
>0
=
a
2
b
2
c
2
+
-
2x
-
3
=
0
x
2
>0
x
2
=
2
x
2
两三角形面积相等
a
+
b为偶数
a
>0且
b
>0
以a、b、c
为三边
,且c为最大边的三角形是RtΔ
=
-1
x
p
q
p
q
q
p
下面两栏中的p与q之间存在何种关系?
(1)哪些p
q?
(2)哪些q
p?
(3)哪些既能
又能
?
6
答案:
(2)q
p
:
p
q
q
(3)既能
p
:
又能
(1)p
q
:
1
2
3
4
5
6
7
x
>0
x
=
√2
两三角形全等
a、b为奇数
ab
>0
=
a
2
b
2
c
2
+
-
2x
-
3
=
0
x
2
>0
x
2
=
2
x
2
两三角形面积相等
a
+
b为偶数
a
>0且
b
>0
以a、b、c
为三边
,且c为最大边的三角形是RtΔ
=
-1
x
p
q
1
2
3
4
(6)
7
5
(6)
观察
1、2
、3、4
充分条件的定义
必要条件的定义
一般地,“若p,则q”为真命题,即
,
p
q
同时,称q是p成立的必要条件.
因为p成立就有充分的理由得出q成立.
所以q成立是p成立必不可少的条件.
非q
非p
此时
我们就说,p是q成立的充分条件.
观察
6
充要条件的定义
如果p成立时,q必然成立,即
,而且q成立时,p也必然成立,即
.
这时我们就说,p是q成立的充分必要条件,简称p是q的充要条件,记作
或
.
p
q
q
p
p
q
q
p
当
,而且
.
这时我们就说,p是q的既不充分也不必要条件
.
q
p
p
q
例1.
指出下列各组命题中,那些p是q的充分条件?
是
是
否
例2
下列”若p,则q”形式的命题中,那些命
题q是p的必要条件?
是
是
否
1.用符号“
”与“
”填空:
(1)
x
=
0
xy
=
0.
(2)
xy
=
0
x
=
0.
(3)
两个角相等
两个角是对顶角.
(4)
两个角是对顶角
两个角相等.
练一练
2.下列各组命题中,p是q的什么条件,q是p的什么条件:
(1)
p:a
∈
Q
,q:
a
∈
R
.
(2)
p:a
∈
R
,q:
a
∈
Q
.
(3)
p:内错角相等,q:两直线平行.
(4)
p:两直线平行,q:内错角相等.
Key
:
p
是q
的充分条件
q
是p
的必要条件
Key
:
p
是q
的必要条件
q
是p
的充分条件
Key
:
p
是q
的充分条件
q
是p
的必要条件
Key
:
p
是q
的充分条件
q
是p
的必要条件
p
是q
的充要条件
(1)
p:(x
-
2)(x
-
3)
=
0
;
q:x
–
2
=
0.
(2)
p:同位角相等
;
q:两直线平行.
(3)
p:
x
=
3
;
q:
.
(4)
p:四边形的对角线相等,q:四边形是平行四边形.
x
2
=
9
例2.
指出下列各组命题中,p是q的什么条件(在“充分而不必要
条件”、“必要而不充分条件”、“充要条件”、“既不充分
也不必要”中选出一种?
x
–
2
=
0
(x
–
2)(x
-
3)
=
0
,
(x
–
2)(x
-
3)
=
0
x
–
2
=
0.
所以p是q的必要而不充分条件.
同位角相等
两直线平行.
所以p是q的充要条件.
(1)
p:(x
-
2)(x
-
3)
=
0
;
q:x
–
2
=
0.
解:
(2)
p:同位角相等
;
q:两直线平行.
解:
(4)
p:四边形的对角线相等,q:四边形是平行四边形.
x
=
3
,
,
所以p是q的充分而不必要条件.
x
2
=
9
=
3
x
x
2
=
9
四边形的对角线相等
四边形是平行四边形,
四边形是平行四边形
四边形的对角线相等.
所以p是q的既不充分也不必要条件.
x
2
=
9
(3)
p:
x
=
3
;
q:
.
解:
解:
a
=
b
=
0
b
2
-
2ab
+
a
2
x=
√3x+4
1.从
“
”、“
”与“
”中选出适当的符号填空:
(1)
x
>
-1
x
>
1.
(2)
.
(3)
a=b
a
+
c
=
b
+
c
.
(4)
.
=
x
2
3x+4
练一练
2.从“充分而不必要条件”、“必要而不充分条件”、“充要
条件”中选出适当的一种填空:
(1)
“
a
=
b
”
是
“
ac
=
bc
”
的
.
(2)
“
两个三角形全等
”
是
“
两个三角形相似
”
的
.
(3)
“
a+
5是无理数”
是
“
a无理数
”
的
.
(4)
“
四边形的两条对角线相等
”
是
“
四边形是矩形
”
的
.
充分而不必要条件
充分而不必要条件
充要条件
必要而不充分条件
现规定电路中,记“开关K
闭合”为p,“灯泡L
点亮”为q,
指出下列各电路图中p是q的什么条件?
:灯泡L
:开
关
:电
源
图
示
K
(A)
(B)
(C)
(D)
L
L
L
L
K
K
K
A
A
素质拓展与学科渗透
p
是q
的
充要条件
p
是q
的
必要而不
充分条件
p
是q
的
充分而不
必要条件
p
是q
的既
不充分也不
必要条件
由B是C的充分条件可得,B
C
由D是C的必要条件可得,C
D
由D是B的充分条件可得,D
B
由A是C的充分条件可得,A
C
A
D
C
B
因而可得,
(1)
D是C的充要条件.
(2)
A是B的充分而不必要条件.
设A是C的充分条件,B是C的充分条件,D是C的必要条件,
D是B的充分条件,则
(1)
D是C的什么条件?
(2)
A是B的什么条件?
解:
机动例题
1
已知“
p:m<-
3
,
q:方程
无实根”,
指出p是q的什么条件?
=
0
m
-
x
-
x
2
=
0
m
-
x
-
x
2
方程
无实根,则
1
4
Δ=
(-
1)
–4·1·
(-
m)
=
1
+
4m
<
0
即m
<
- .
2
=
0
m
-
x
-
x
2
∴m
<
-3
方程
无实根.
∴p是q的充分条件.
=
0
m
-
x
-
x
2
∵方程
无实根
m
<
-3,
∴p不是q的必要条件.
∴综上所述,p是q的充分而不必要条件.
解:
机动例题
2
机动练习
从“充分而不必要条件”、“必要而不充分条件”、“充要
条件”或“既不充分也不必要条件”中选出适当的一种填空:
(1)
“
A
B
”
是
“
A∩B
=
A
”
的
.
(2)
“
x∈A
”
是
“
x∈A∩B
”
的
.
(3)
“
a=b=0
”
是
“
ab=0
”
的
.
(4)
“
0”
是
“
x
-
2
<
5”
的
.
(5)
“
二次函数
的图象过原点
”
是
“
c
=
0
”
的
.
y=
+bx
+
c(a
≠
0)
ax
2
充分而不必要条件
必要而不充分条件
充分而不必要条件
充分而不必要条件
充要条件
应
用
充分条件
定
义
充要条件
必要条件
新
知
小
结
作业:P12
A组
2、3、4
§1.2
充分条件与必要条件
旧知温习
原命题
若p则q
逆命题
若q则p
否命题
若﹁
p则﹁
q
逆否命题
若﹁
q则﹁p
互为逆否
同真同假
互为逆否
同真同假
互逆命题
真假无关
互逆命题
真假无关
互否命题真假无关
互否命题真假无关
符号
与
的介绍
如果命题为真,即如果p成立,那么q一定成立,
记作
,读作
“
p推出
q
”.
p
q
如果命题为假,即如果p成立,那么q不成立,
记作
,读作
“
p推不出
q
”.
p
q
现有命题“若p则q”,
新知准备
定义:如果命题“若p,则q”为真命题,即p
?
q,
那么我们就说p是q的充分条件;q是p的必要条件.
【定义得出】
①充分性:条件是充分的,也就是说条件是充足的,足够的,足以保证的。符合“若p则q”为真(p=>q)的形式,即“有之必成立”。
②必要性:必要就是必须的,必不可少的。符合“若非q则非p”
为真(非q=>非p)的形式,即“无之必不成立”。
注:
③p是q的充分条件与q是p的必要条件是完全等价的,它们是同一个逻辑关系“p=>q”的不同表达方法。
问题
?
1
2
3
4
5
6
7
x
>0
x
=
√2
两三角形全等
a、b为奇数
ab
>0
=
a
2
b
2
c
2
+
-
2x
-
3
=
0
x
2
>0
x
2
=
2
x
2
两三角形面积相等
a
+
b为偶数
a
>0且
b
>0
以a、b、c
为三边
,且c为最大边的三角形是RtΔ
=
-1
x
p
q
p
q
q
p
下面两栏中的p与q之间存在何种关系?
(1)哪些p
q?
(2)哪些q
p?
(3)哪些既能
又能
?
6
答案:
(2)q
p
:
p
q
q
(3)既能
p
:
又能
(1)p
q
:
1
2
3
4
5
6
7
x
>0
x
=
√2
两三角形全等
a、b为奇数
ab
>0
=
a
2
b
2
c
2
+
-
2x
-
3
=
0
x
2
>0
x
2
=
2
x
2
两三角形面积相等
a
+
b为偶数
a
>0且
b
>0
以a、b、c
为三边
,且c为最大边的三角形是RtΔ
=
-1
x
p
q
1
2
3
4
(6)
7
5
(6)
观察
1、2
、3、4
充分条件的定义
必要条件的定义
一般地,“若p,则q”为真命题,即
,
p
q
同时,称q是p成立的必要条件.
因为p成立就有充分的理由得出q成立.
所以q成立是p成立必不可少的条件.
非q
非p
此时
我们就说,p是q成立的充分条件.
观察
6
充要条件的定义
如果p成立时,q必然成立,即
,而且q成立时,p也必然成立,即
.
这时我们就说,p是q成立的充分必要条件,简称p是q的充要条件,记作
或
.
p
q
q
p
p
q
q
p
当
,而且
.
这时我们就说,p是q的既不充分也不必要条件
.
q
p
p
q
例1.
指出下列各组命题中,那些p是q的充分条件?
是
是
否
例2
下列”若p,则q”形式的命题中,那些命
题q是p的必要条件?
是
是
否
1.用符号“
”与“
”填空:
(1)
x
=
0
xy
=
0.
(2)
xy
=
0
x
=
0.
(3)
两个角相等
两个角是对顶角.
(4)
两个角是对顶角
两个角相等.
练一练
2.下列各组命题中,p是q的什么条件,q是p的什么条件:
(1)
p:a
∈
Q
,q:
a
∈
R
.
(2)
p:a
∈
R
,q:
a
∈
Q
.
(3)
p:内错角相等,q:两直线平行.
(4)
p:两直线平行,q:内错角相等.
Key
:
p
是q
的充分条件
q
是p
的必要条件
Key
:
p
是q
的必要条件
q
是p
的充分条件
Key
:
p
是q
的充分条件
q
是p
的必要条件
Key
:
p
是q
的充分条件
q
是p
的必要条件
p
是q
的充要条件
(1)
p:(x
-
2)(x
-
3)
=
0
;
q:x
–
2
=
0.
(2)
p:同位角相等
;
q:两直线平行.
(3)
p:
x
=
3
;
q:
.
(4)
p:四边形的对角线相等,q:四边形是平行四边形.
x
2
=
9
例2.
指出下列各组命题中,p是q的什么条件(在“充分而不必要
条件”、“必要而不充分条件”、“充要条件”、“既不充分
也不必要”中选出一种?
x
–
2
=
0
(x
–
2)(x
-
3)
=
0
,
(x
–
2)(x
-
3)
=
0
x
–
2
=
0.
所以p是q的必要而不充分条件.
同位角相等
两直线平行.
所以p是q的充要条件.
(1)
p:(x
-
2)(x
-
3)
=
0
;
q:x
–
2
=
0.
解:
(2)
p:同位角相等
;
q:两直线平行.
解:
(4)
p:四边形的对角线相等,q:四边形是平行四边形.
x
=
3
,
,
所以p是q的充分而不必要条件.
x
2
=
9
=
3
x
x
2
=
9
四边形的对角线相等
四边形是平行四边形,
四边形是平行四边形
四边形的对角线相等.
所以p是q的既不充分也不必要条件.
x
2
=
9
(3)
p:
x
=
3
;
q:
.
解:
解:
a
=
b
=
0
b
2
-
2ab
+
a
2
x=
√3x+4
1.从
“
”、“
”与“
”中选出适当的符号填空:
(1)
x
>
-1
x
>
1.
(2)
.
(3)
a=b
a
+
c
=
b
+
c
.
(4)
.
=
x
2
3x+4
练一练
2.从“充分而不必要条件”、“必要而不充分条件”、“充要
条件”中选出适当的一种填空:
(1)
“
a
=
b
”
是
“
ac
=
bc
”
的
.
(2)
“
两个三角形全等
”
是
“
两个三角形相似
”
的
.
(3)
“
a+
5是无理数”
是
“
a无理数
”
的
.
(4)
“
四边形的两条对角线相等
”
是
“
四边形是矩形
”
的
.
充分而不必要条件
充分而不必要条件
充要条件
必要而不充分条件
现规定电路中,记“开关K
闭合”为p,“灯泡L
点亮”为q,
指出下列各电路图中p是q的什么条件?
:灯泡L
:开
关
:电
源
图
示
K
(A)
(B)
(C)
(D)
L
L
L
L
K
K
K
A
A
素质拓展与学科渗透
p
是q
的
充要条件
p
是q
的
必要而不
充分条件
p
是q
的
充分而不
必要条件
p
是q
的既
不充分也不
必要条件
由B是C的充分条件可得,B
C
由D是C的必要条件可得,C
D
由D是B的充分条件可得,D
B
由A是C的充分条件可得,A
C
A
D
C
B
因而可得,
(1)
D是C的充要条件.
(2)
A是B的充分而不必要条件.
设A是C的充分条件,B是C的充分条件,D是C的必要条件,
D是B的充分条件,则
(1)
D是C的什么条件?
(2)
A是B的什么条件?
解:
机动例题
1
已知“
p:m<-
3
,
q:方程
无实根”,
指出p是q的什么条件?
=
0
m
-
x
-
x
2
=
0
m
-
x
-
x
2
方程
无实根,则
1
4
Δ=
(-
1)
–4·1·
(-
m)
=
1
+
4m
<
0
即m
<
- .
2
=
0
m
-
x
-
x
2
∴m
<
-3
方程
无实根.
∴p是q的充分条件.
=
0
m
-
x
-
x
2
∵方程
无实根
m
<
-3,
∴p不是q的必要条件.
∴综上所述,p是q的充分而不必要条件.
解:
机动例题
2
机动练习
从“充分而不必要条件”、“必要而不充分条件”、“充要
条件”或“既不充分也不必要条件”中选出适当的一种填空:
(1)
“
A
B
”
是
“
A∩B
=
A
”
的
.
(2)
“
x∈A
”
是
“
x∈A∩B
”
的
.
(3)
“
a=b=0
”
是
“
ab=0
”
的
.
(4)
“
0
是
“
x
-
2
<
5”
的
.
(5)
“
二次函数
的图象过原点
”
是
“
c
=
0
”
的
.
y=
+bx
+
c(a
≠
0)
ax
2
充分而不必要条件
必要而不充分条件
充分而不必要条件
充分而不必要条件
充要条件
应
用
充分条件
定
义
充要条件
必要条件
新
知
小
结
作业:P12
A组
2、3、4
