人教版 八册下册19.1.2-函数的图象(1)课件(共26张PPT)
文档属性
| 名称 | 人教版 八册下册19.1.2-函数的图象(1)课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:12:42 | ||
图片预览





文档简介
19.1.2.函数的图象
(第1课时)
我们在前面学习了函数意义,并掌握了函数关系式的确立。但有些函数问题很难用函数关系式表示出来,然而可以通过图来直观反映。
例如某地日气温随时间的变化关系
导入新课
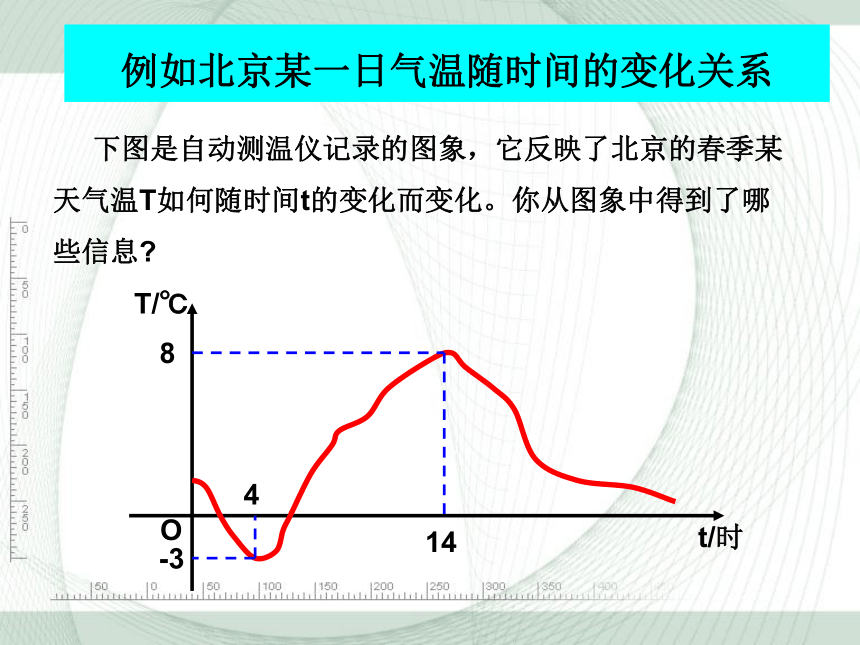
下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?
14
4
8
O
-3
t/时
T/℃
例如北京某一日气温随时间的变化关系
我们这节课就来解决如何画函数图象的问题及解读函数图象信息.
即使对于能列式表示的函数关系,如果也能画图表示则会使函数关系更清晰.
正方形的边长为x,面积为s。面积s是不是边长x的函数?如果是,它们的函数关系式怎样表示?
面积s与边长x的函数关系式为:
s = x2
从式子s = x2来看,边长x越大,面积s也越大。能不能用图象直观的反映出来呢?
你知道为什么“x>0” ?
(x>0)
探究一
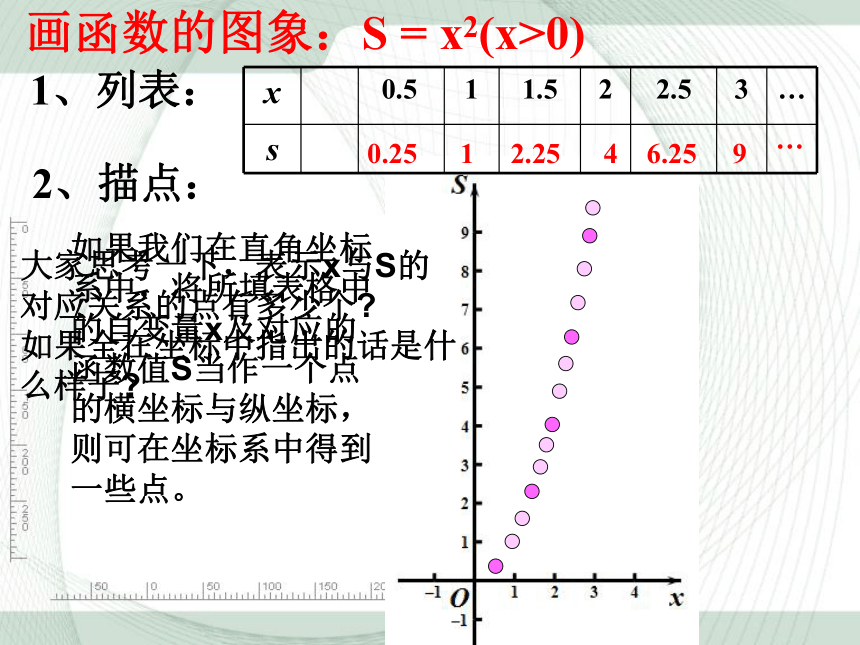
画函数的图象:S = x2(x>0)
x
0.5
1
1.5
2
2.5
3
…
s
1、列表:
2、描点:
1
0.25
4
9
2.25
6.25
…
如果我们在直角坐标系中,将所填表格中的自变量x及对应的函数值S当作一个点的横坐标与纵坐标,则可在坐标系中得到一些点。
大家思考一下,表示x与S的对应关系的点有多少个?
如果全在坐标中指出的话是什么样子?
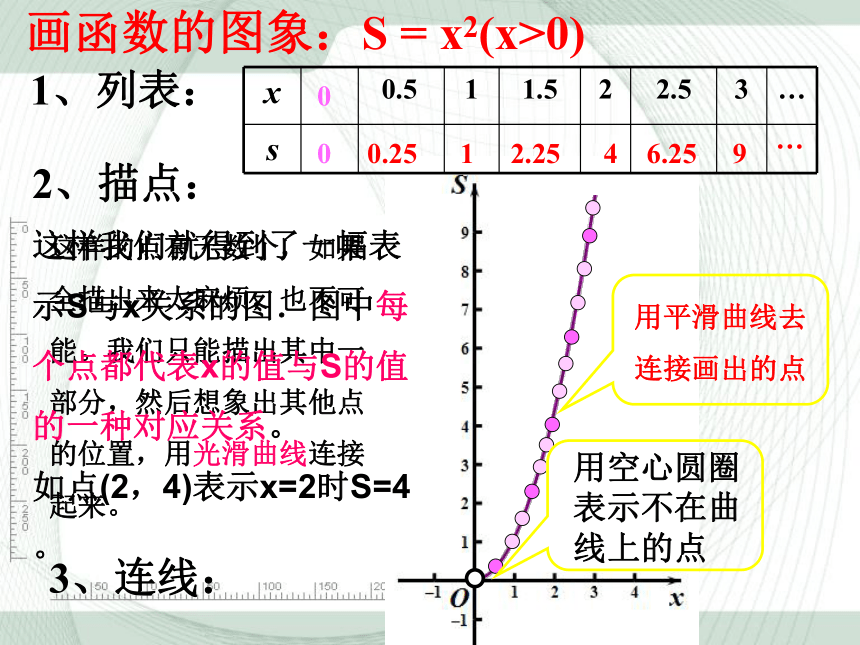
画函数的图象:S = x2(x>0)
x
0.5
1
1.5
2
2.5
3
…
s
1、列表:
2、描点:
3、连线:
用平滑曲线去连接画出的点
1
0.25
4
9
2.25
6.25
0
0
…
这样的点有无数个,如果全描出来太麻烦,也不可能。我们只能描出其中一部分,然后想象出其他点的位置,用光滑曲线连接起来。
用空心圆圈表示不在曲线上的点
这样我们就得到了一幅表
示S与x关系的图.图中每
个点都代表x的值与S的值
的一种对应关系。
如点(2,4)表示x=2时S=4。
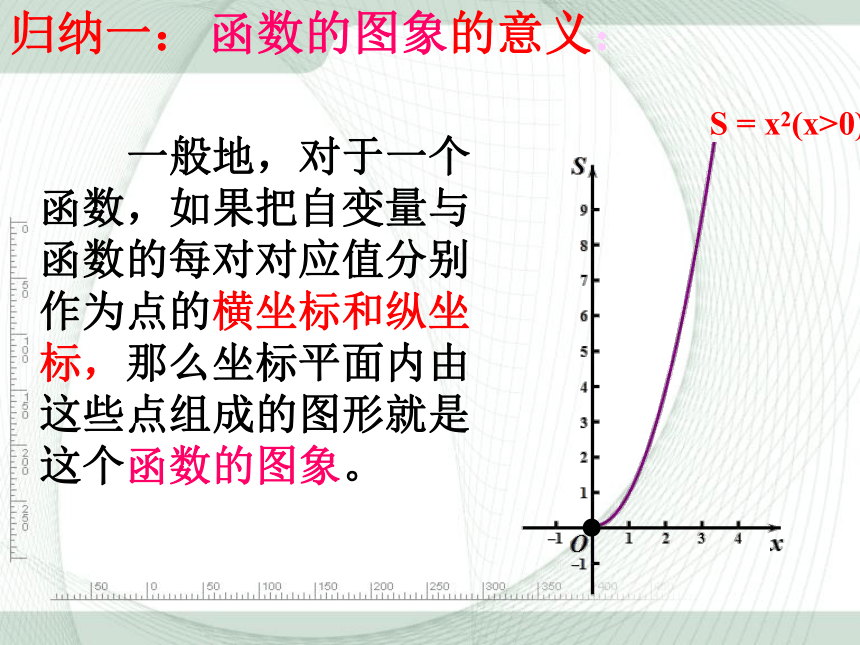
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
函数的图象的意义:
归纳一:
S = x2(x>0)
3、连线
函数图象的画法:
1、列表
2、描点
列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),并取值要适当,以便画图.
建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值
对应的各点
按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来
归纳二:
注:函数图象可能是曲线,也可能是直线,也可能是线段或射线,函数图象的形状取决于函数关系和自变量的取值范围。
例1.画出下列函数的图象(1)y=x+0.5
①列表
(自变量x取一切实数)
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
②描点
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=x+0.5
③连线
指出该函数图象有什么性质?
函数y随x的增大而增大
函数的图象是一条直线
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=x+0.5
①点(2.5 ,3)是否在此函数的图象上?
②若点(-5,b)在此函数的图象上,则b=
( )
③若此函数的图象与x轴交于点A,则A点坐标是( ) 若此函数的图象与y轴交于点B,则B点坐标是( )
思考:
-4.5
-0.5,0
0,0.5
例2.画出下列函数的图象
(x>0)
x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
y
4
1
1
6
5
2
3
0
x
2
3
4
5
6
函数y随x的增大而减小
指出该函数图象有什么性质?
强调:
1、列表时,要考虑自变量的取值范围,合理的选择具有代表性的自变量的取值和函数值的对应值列成表格。
2、描点时,要把自变量作为点的横坐标,对应的函数值作为纵坐标。
3、连线时,要按自变量由小到大的顺序依次连接各点,要注意图象的发展趋势。
.
图象上的点与函数关系式的关系:
(1)函数图象上的任意点(x,y)中的x、y满足函数关系式;
(2)满足函数关系式的任意一对(x,y)的值,所对应的点一定在函数图象上。
归纳:
判断点在函数图象上的方法:
将这个点的坐标(x, y)代入函数解析式中,若满足函数解析式,那么点就在函数的图象上;如果不满足函数解析式,那么点就不在函数的图象上。
探 索 归 纳
尝试应用:
1、已知点(-1,2)是函数y=kx的图象上的一点,则
k= 。
2、下列各点中,在函数y= 图象上的是( )
A.(-2,-4) B.(4,4) C.(-2,4) D.(4,2)
3、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A.(1,3) B.(1,2) C.(1,1) D.(2,1)
-2
D
B
4.下列四个点中在函数y=2x—3的图象上有( )个 (1,2) 、(3,3) 、(-1, -1)、 (1.5,0)
A.1 B.2 C.3 D.4
B
观察:下图是自动测温仪记录的图象,它反映了北京春季某天气温T如何随时间t的变化而变化,你从图中得到哪些信息?
探究二
14
4
8
O
-3
t/时
T/℃
(2)这一天什么时间气温最低?什么时间气温最高?
(3)哪个时间段气温呈下降状态,哪个时间段气温呈上升状态?
4时气温最底-3℃
14时最高气温8℃
下降:0时至4时,14时至24时.
上升:4时至14时
(1)因为时间t对应气温T是唯一值,所以气温T是时间t的函数.
归纳
14
4
8
O
-3
t/时
T/℃
y/千米
时间x/分钟
0
1.1
2
15
25
37
55
80
例2、下面的图象反映的过程是:小明从家里出发去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.
根据图象回答下列问题:
1、菜地离小明家多远?小明走到菜地用了多少时间?
从纵坐标看:菜地离小明家1.1千米.
从横坐标看:小明走到菜地用了15分钟.
3、菜地离玉米地多远?小明从菜地走到玉米地用了多少时间?
4、小明给玉米地锄草用了多少时间?
y/千米
时间x/分钟
0
1.1
2
15
25
37
55
80
2、小明给菜地浇水用了多少时间?
从横坐标看:小明给菜地浇水用了10分钟(即25-15)
从纵坐标看:菜地离玉米地0.9千米.
从横坐标看:小明从菜地用到玉米地用了12分钟.
从横坐标看:小明给玉米地锄草用了18分钟(即55-37)
5、玉米地离小明家多远?小明从玉米地走回家的平均速度是多少?
y/千米
时间x/分钟
0
1.1
2
15
25
37
55
80
从纵坐标看:玉米地离小明家2千米.
从横坐标看:小明从玉米地走回家用了25分钟.
平均速度是0.08千米/分.
1.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )
D
尝试应用
2、柿子熟了,从树上落下来,下面的哪一幅图可以大致刻画出柿子下落过程中的速度变化情况?
速度
时间
0
0
0
0
①
②
③
④
速度
速度
速度
时间
时间
时间
4、下图表示的是,小明放学回家途中骑车速度与时间的关系。你能想像出他回家路上的情景吗?
速度
时间
0
补偿提高
总结提高
1、函数图象上点的横、纵坐标分别对应 值和 的值。
自变量
函数
2、从函数图象中获得的信息来研究实际问题关键要注意分清横轴和纵轴表示的
实际含义
3、描点法画函数图象的一般步骤:(1) ____, (2)____, (3)______
列表
描点
连线
(第1课时)
我们在前面学习了函数意义,并掌握了函数关系式的确立。但有些函数问题很难用函数关系式表示出来,然而可以通过图来直观反映。
例如某地日气温随时间的变化关系
导入新课
下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间t的变化而变化。你从图象中得到了哪些信息?
14
4
8
O
-3
t/时
T/℃
例如北京某一日气温随时间的变化关系
我们这节课就来解决如何画函数图象的问题及解读函数图象信息.
即使对于能列式表示的函数关系,如果也能画图表示则会使函数关系更清晰.
正方形的边长为x,面积为s。面积s是不是边长x的函数?如果是,它们的函数关系式怎样表示?
面积s与边长x的函数关系式为:
s = x2
从式子s = x2来看,边长x越大,面积s也越大。能不能用图象直观的反映出来呢?
你知道为什么“x>0” ?
(x>0)
探究一
画函数的图象:S = x2(x>0)
x
0.5
1
1.5
2
2.5
3
…
s
1、列表:
2、描点:
1
0.25
4
9
2.25
6.25
…
如果我们在直角坐标系中,将所填表格中的自变量x及对应的函数值S当作一个点的横坐标与纵坐标,则可在坐标系中得到一些点。
大家思考一下,表示x与S的对应关系的点有多少个?
如果全在坐标中指出的话是什么样子?
画函数的图象:S = x2(x>0)
x
0.5
1
1.5
2
2.5
3
…
s
1、列表:
2、描点:
3、连线:
用平滑曲线去连接画出的点
1
0.25
4
9
2.25
6.25
0
0
…
这样的点有无数个,如果全描出来太麻烦,也不可能。我们只能描出其中一部分,然后想象出其他点的位置,用光滑曲线连接起来。
用空心圆圈表示不在曲线上的点
这样我们就得到了一幅表
示S与x关系的图.图中每
个点都代表x的值与S的值
的一种对应关系。
如点(2,4)表示x=2时S=4。
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横坐标和纵坐标,那么坐标平面内由这些点组成的图形就是这个函数的图象。
函数的图象的意义:
归纳一:
S = x2(x>0)
3、连线
函数图象的画法:
1、列表
2、描点
列出自变量与函数的对应值表。
注意:自变量的值(满足取值范围),并取值要适当,以便画图.
建立直角坐标系,以自变量的值为横坐标,
相应的函数值为纵坐标,描出表格中数值
对应的各点
按照横坐标从小到大的顺序把描出的点用
平滑曲线依次连接起来
归纳二:
注:函数图象可能是曲线,也可能是直线,也可能是线段或射线,函数图象的形状取决于函数关系和自变量的取值范围。
例1.画出下列函数的图象(1)y=x+0.5
①列表
(自变量x取一切实数)
x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
②描点
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=x+0.5
③连线
指出该函数图象有什么性质?
函数y随x的增大而增大
函数的图象是一条直线
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=x+0.5
①点(2.5 ,3)是否在此函数的图象上?
②若点(-5,b)在此函数的图象上,则b=
( )
③若此函数的图象与x轴交于点A,则A点坐标是( ) 若此函数的图象与y轴交于点B,则B点坐标是( )
思考:
-4.5
-0.5,0
0,0.5
例2.画出下列函数的图象
(x>0)
x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
12
6
4
3
2.4
2
1.5
1.2
1
…
y
4
1
1
6
5
2
3
0
x
2
3
4
5
6
函数y随x的增大而减小
指出该函数图象有什么性质?
强调:
1、列表时,要考虑自变量的取值范围,合理的选择具有代表性的自变量的取值和函数值的对应值列成表格。
2、描点时,要把自变量作为点的横坐标,对应的函数值作为纵坐标。
3、连线时,要按自变量由小到大的顺序依次连接各点,要注意图象的发展趋势。
.
图象上的点与函数关系式的关系:
(1)函数图象上的任意点(x,y)中的x、y满足函数关系式;
(2)满足函数关系式的任意一对(x,y)的值,所对应的点一定在函数图象上。
归纳:
判断点在函数图象上的方法:
将这个点的坐标(x, y)代入函数解析式中,若满足函数解析式,那么点就在函数的图象上;如果不满足函数解析式,那么点就不在函数的图象上。
探 索 归 纳
尝试应用:
1、已知点(-1,2)是函数y=kx的图象上的一点,则
k= 。
2、下列各点中,在函数y= 图象上的是( )
A.(-2,-4) B.(4,4) C.(-2,4) D.(4,2)
3、点A(1,m)在函数y=2x的图象上,则点的坐标是( )
A.(1,3) B.(1,2) C.(1,1) D.(2,1)
-2
D
B
4.下列四个点中在函数y=2x—3的图象上有( )个 (1,2) 、(3,3) 、(-1, -1)、 (1.5,0)
A.1 B.2 C.3 D.4
B
观察:下图是自动测温仪记录的图象,它反映了北京春季某天气温T如何随时间t的变化而变化,你从图中得到哪些信息?
探究二
14
4
8
O
-3
t/时
T/℃
(2)这一天什么时间气温最低?什么时间气温最高?
(3)哪个时间段气温呈下降状态,哪个时间段气温呈上升状态?
4时气温最底-3℃
14时最高气温8℃
下降:0时至4时,14时至24时.
上升:4时至14时
(1)因为时间t对应气温T是唯一值,所以气温T是时间t的函数.
归纳
14
4
8
O
-3
t/时
T/℃
y/千米
时间x/分钟
0
1.1
2
15
25
37
55
80
例2、下面的图象反映的过程是:小明从家里出发去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.
根据图象回答下列问题:
1、菜地离小明家多远?小明走到菜地用了多少时间?
从纵坐标看:菜地离小明家1.1千米.
从横坐标看:小明走到菜地用了15分钟.
3、菜地离玉米地多远?小明从菜地走到玉米地用了多少时间?
4、小明给玉米地锄草用了多少时间?
y/千米
时间x/分钟
0
1.1
2
15
25
37
55
80
2、小明给菜地浇水用了多少时间?
从横坐标看:小明给菜地浇水用了10分钟(即25-15)
从纵坐标看:菜地离玉米地0.9千米.
从横坐标看:小明从菜地用到玉米地用了12分钟.
从横坐标看:小明给玉米地锄草用了18分钟(即55-37)
5、玉米地离小明家多远?小明从玉米地走回家的平均速度是多少?
y/千米
时间x/分钟
0
1.1
2
15
25
37
55
80
从纵坐标看:玉米地离小明家2千米.
从横坐标看:小明从玉米地走回家用了25分钟.
平均速度是0.08千米/分.
1.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )
D
尝试应用
2、柿子熟了,从树上落下来,下面的哪一幅图可以大致刻画出柿子下落过程中的速度变化情况?
速度
时间
0
0
0
0
①
②
③
④
速度
速度
速度
时间
时间
时间
4、下图表示的是,小明放学回家途中骑车速度与时间的关系。你能想像出他回家路上的情景吗?
速度
时间
0
补偿提高
总结提高
1、函数图象上点的横、纵坐标分别对应 值和 的值。
自变量
函数
2、从函数图象中获得的信息来研究实际问题关键要注意分清横轴和纵轴表示的
实际含义
3、描点法画函数图象的一般步骤:(1) ____, (2)____, (3)______
列表
描点
连线
