人教版八年级数学下册 第二十章《数据的分析》复习 课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第二十章《数据的分析》复习 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 372.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:11:45 | ||
图片预览




文档简介
第二十章
《数据的分析》复习
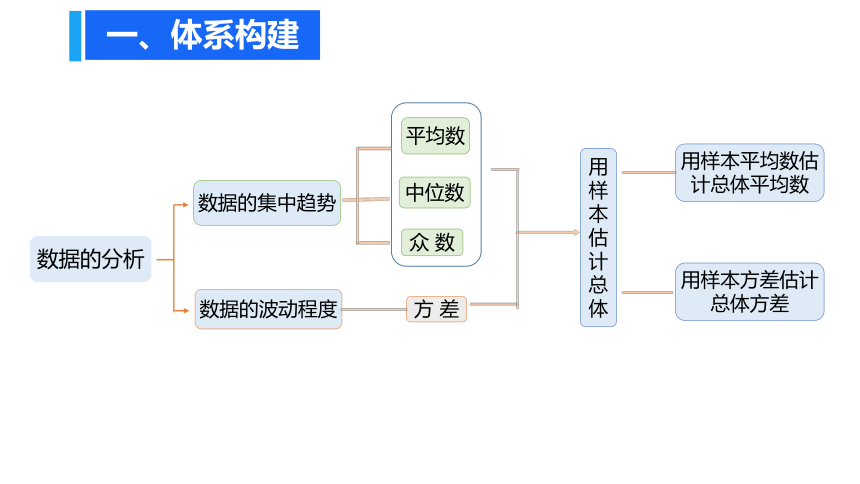
一、体系构建
平均数
数据的分析
数据的集中趋势
中位数
众 数
方 差
数据的波动程度
用样本估计总体
用样本平均数估计总体平均数
用样本方差估计总体方差
二、例题教学
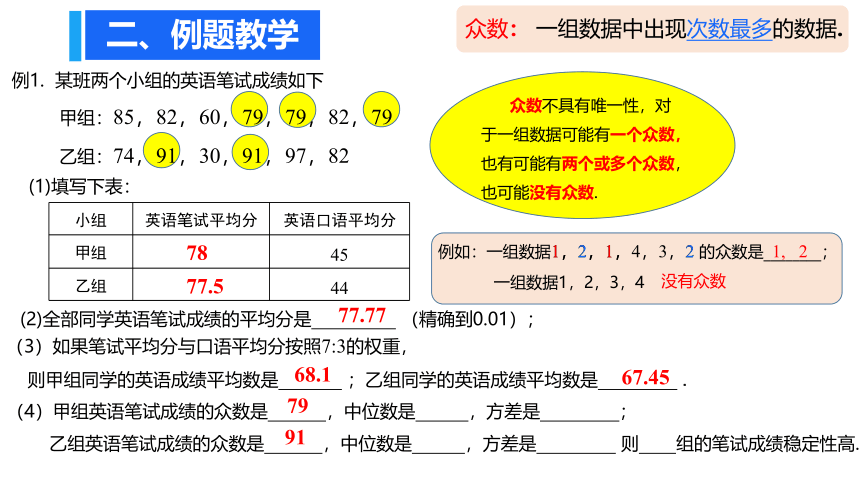
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
(1)分析:
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
算术平均数:
x1+x2+ x3+ ··· + xn
n
????=
?
77.77
或
????甲=
?
????乙=
?
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
若n个数x1,x2,…xn的权分别是w1,w2,…wn,则
叫做这n个数的加权平均数.
(3)分析:
????甲=78×7+45×37+3=68.1
?
????乙=77.5×7+44×37+3=67.45
?
68.1
67.45
7
3
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
68.1
67.45
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
(4)分析:
众数甲:79
众数乙:91
众数: 一组数据中出现次数最多的数据.
79
91
众数不具有唯一性,对于一组数据可能有一个众数,也有可能有两个或多个众数,也可能没有众数.
例如:一组数据1,2,1,4,3,2 的众数是________;
1, 2
1,2,1, 2
一组数据1,2,3,4
没有众数
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
68.1
67.45
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
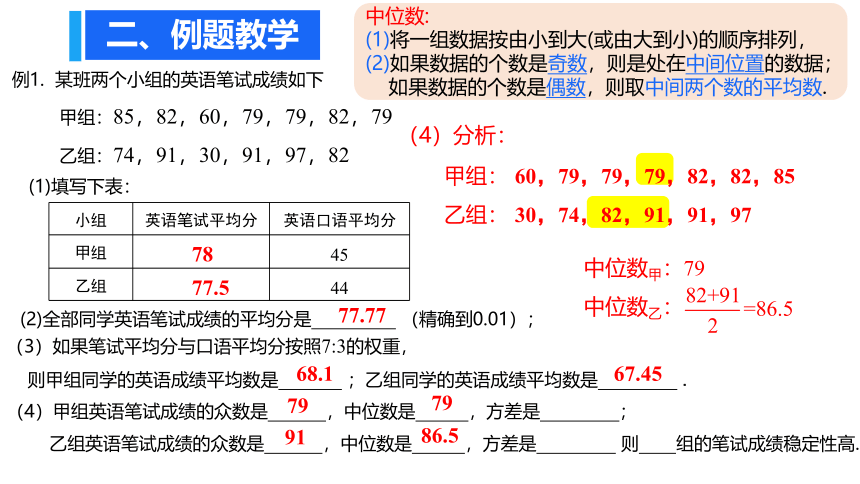
中位数:
(1)将一组数据按由小到大(或由大到小)的顺序排列,
(2)如果数据的个数是奇数,则是处在中间位置的数据;
如果数据的个数是偶数,则取中间两个数的平均数.
(4)分析:
甲组: 60,79,79,79,82,82,85
乙组: 30,74,82,91,91,97
中位数甲:79
中位数乙:
79
91
79
86.5
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
(4)分析:
方差:
数据的波动性:方差越大,数据的波动越大;
方差越小,数据的波动越小.
????2=1????[(????1?????)2+(????2?????)2+…+(?????????????)2]
?
77.77
68.1
67.45
79
91
79
86.5
∵58.29<505.58 ∴甲组的成绩比较稳定
58.29
505.58
甲
77.5
78
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
68.1
67.45
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
79
91
79
86.5
58.29
505.58
甲
算术平均数:
加权平均数:
众数: 一组数据中出现次数最多的数据.
中位数:
(1)将一组数据按由小到大(或由大到小)的顺序排列,
(2)如果数据的个数是奇数,则是处在中间位置的数据;
如果数据的个数是偶数,则取中间两个数的平均数.
方差:
数据的波动性:方差越大,数据的波动越大;
方差越小,数据的波动越小.
????=
?
x1+x2+ x3+ ··· + xn
n
例2. 甲、乙两组数据(单位:厘米)如下表:
(1)根据以上数据填表:
(2)哪一组数据较稳定?
三、方法迁移
173
173
1.8
0.6
(2)解:∵0.6<1.8 即 <
∴ 甲组的成绩比较稳定
173
173
四、思维提升
例3. (人教八下P119例6)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19 22 17 16 19 32
30 16 14 15 26 15 32 23 17 15 15 28 28 16 19
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由;
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?
说明理由.
四、思维提升
17 18 16 13 24 15 28 26 18 19 22 17 16 19 32
30 16 14 15 26 15 32 23 17 15 15 28 28 16 19
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
整理下列数据:
共30个
频数分布表
条形图
四、思维提升
5
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
1
1
4
3
2
答:这个服装部营业员的月销售额为15万元的人数最多,中间的月销售额是18万元,平均月销售额约为20万元.
众数
中位数
平均数
15
18
20
共30人
四、思维提升
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由;
在众数、中位数和平均数中, 平均数最大。
(2)解:如果想确定一个较高的销售目标,月销售额可以定为每月20万元(平均数).理由如下:
众数:15,中位数:18,平均数:20
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
11人
共30人
可以估计,月销售额定为每月20万元是一
个较高目标,此时大约会 有 的营业员获得奖励.
四、思维提升
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?
说明理由.
(3)解:月销售额可以定为每月18万元(中位数). 理由如下:
因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右,可以估计,
如果月销售额定为18万元,将有一半左右的营业员获得奖励.
众数:15,中位数:18,平均数:20
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
共30人
16人
五、总结凝炼
一种思想
两个公式
四个概念
样本估计总体的统计思想
加权平均数:
加权平均数
方差:
中位数
众数
方差
六、课后作业
归纳
1.某中学“环保小组”的5名同学在一次活动中捡废弃塑料袋的个数分别是
4, 6,8,8,10,这组数据的众数为( )
A. 4 B. 6 C. 8 D. 10
2. 某校5名同学在“国学经典诵读”比赛中,成绩(单位:分)分别是86,95,
97,90,88,这组数据的中位数是( )
A. 97 B. 90 C. 95 D. 88
3. 若一组数据1,2,3,n的平均数是2,则这组数据的方差为( )
A. 1 B. 2 C. 3 D.
C
B
D
六、课后作业
归纳
4. 甲、乙两人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为 =0.63, =0.51,则两人中成绩最稳定的是( )
A. 甲 B. 乙 C. 一样 D. 不确定
5. 宁宁所在的班级有42人,某次考试他的成绩是80分,若全班同学的平均分是78分,判断宁宁的成绩是否在班级属于中等偏上,还需要了解班级成绩的( )
A. 中位数 B. 众数 C. 加权平均数 D. 方差
B
A
六、课后作业
6. (2019云南)某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
{5940675A-B579-460E-94D1-54222C63F5DA}月销售量/件数
1770
480
220
180
120
90
人数
1
1
3
3
3
4
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、
众数中,哪个最适合作为月销售目标?请说明理由.
六、课后作业
解:(1)这15名营业员该月销售量数据的平均数为278件, 中位数为180件,众数为90件;
【解法提示】平均数x= ×(1770+480+220×3+180×3+120×3+90×4)=278(件) ;把这15个数据按从大到小顺的序排列,位于第8个位置的数据是180,∴中位数是180件;在这15个数据中,数据90出现了4次,为出现次数最多的数据,∴众数是90件.
(2)中位数最适合作为销售目标.理由如下:
在这15人中,月销售额不低于278(平均数)件的有2人,月销售额不低于180(中位数)件的有8人,月销售额不低于90(众数)件的有15人.∴如果想让一半左右的营业员都能够达到月销售目标,(1)中的平均数、中位数、众数中,中位数最适合作为月销售目标.
《数据的分析》复习
一、体系构建
平均数
数据的分析
数据的集中趋势
中位数
众 数
方 差
数据的波动程度
用样本估计总体
用样本平均数估计总体平均数
用样本方差估计总体方差
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
(1)分析:
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
算术平均数:
x1+x2+ x3+ ··· + xn
n
????=
?
77.77
或
????甲=
?
????乙=
?
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
若n个数x1,x2,…xn的权分别是w1,w2,…wn,则
叫做这n个数的加权平均数.
(3)分析:
????甲=78×7+45×37+3=68.1
?
????乙=77.5×7+44×37+3=67.45
?
68.1
67.45
7
3
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
68.1
67.45
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
(4)分析:
众数甲:79
众数乙:91
众数: 一组数据中出现次数最多的数据.
79
91
众数不具有唯一性,对于一组数据可能有一个众数,也有可能有两个或多个众数,也可能没有众数.
例如:一组数据1,2,1,4,3,2 的众数是________;
1, 2
1,2,1, 2
一组数据1,2,3,4
没有众数
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
68.1
67.45
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
中位数:
(1)将一组数据按由小到大(或由大到小)的顺序排列,
(2)如果数据的个数是奇数,则是处在中间位置的数据;
如果数据的个数是偶数,则取中间两个数的平均数.
(4)分析:
甲组: 60,79,79,79,82,82,85
乙组: 30,74,82,91,91,97
中位数甲:79
中位数乙:
79
91
79
86.5
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
(4)分析:
方差:
数据的波动性:方差越大,数据的波动越大;
方差越小,数据的波动越小.
????2=1????[(????1?????)2+(????2?????)2+…+(?????????????)2]
?
77.77
68.1
67.45
79
91
79
86.5
∵58.29<505.58 ∴甲组的成绩比较稳定
58.29
505.58
甲
77.5
78
二、例题教学
例1. 某班两个小组的英语笔试成绩如下
甲组:85,82,60,79,79,82,79
乙组:74,91,30,91,97,82
(1)填写下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}小组
英语笔试平均分
英语口语平均分
甲组
?
45
乙组
?
44
78
77.5
(2)全部同学英语笔试成绩的平均分是 (精确到0.01);
(3)如果笔试平均分与口语平均分按照7:3的权重,
则甲组同学的英语成绩平均数是 ;乙组同学的英语成绩平均数是 .
77.77
68.1
67.45
(4)甲组英语笔试成绩的众数是 ,中位数是 ,方差是 ;
乙组英语笔试成绩的众数是 ,中位数是 ,方差是 则 组的笔试成绩稳定性高.
79
91
79
86.5
58.29
505.58
甲
算术平均数:
加权平均数:
众数: 一组数据中出现次数最多的数据.
中位数:
(1)将一组数据按由小到大(或由大到小)的顺序排列,
(2)如果数据的个数是奇数,则是处在中间位置的数据;
如果数据的个数是偶数,则取中间两个数的平均数.
方差:
数据的波动性:方差越大,数据的波动越大;
方差越小,数据的波动越小.
????=
?
x1+x2+ x3+ ··· + xn
n
例2. 甲、乙两组数据(单位:厘米)如下表:
(1)根据以上数据填表:
(2)哪一组数据较稳定?
三、方法迁移
173
173
1.8
0.6
(2)解:∵0.6<1.8 即 <
∴ 甲组的成绩比较稳定
173
173
四、思维提升
例3. (人教八下P119例6)某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成情况对营业员进行适当的奖励.为了确定一个适当的月销售目标,商场服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
17 18 16 13 24 15 28 26 18 19 22 17 16 19 32
30 16 14 15 26 15 32 23 17 15 15 28 28 16 19
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由;
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?
说明理由.
四、思维提升
17 18 16 13 24 15 28 26 18 19 22 17 16 19 32
30 16 14 15 26 15 32 23 17 15 15 28 28 16 19
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
整理下列数据:
共30个
频数分布表
条形图
四、思维提升
5
(1)月销售额在哪个值的人数最多?中间的月销售额是多少?平均月销售额是多少?
1
1
4
3
2
答:这个服装部营业员的月销售额为15万元的人数最多,中间的月销售额是18万元,平均月销售额约为20万元.
众数
中位数
平均数
15
18
20
共30人
四、思维提升
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由;
在众数、中位数和平均数中, 平均数最大。
(2)解:如果想确定一个较高的销售目标,月销售额可以定为每月20万元(平均数).理由如下:
众数:15,中位数:18,平均数:20
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
11人
共30人
可以估计,月销售额定为每月20万元是一
个较高目标,此时大约会 有 的营业员获得奖励.
四、思维提升
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?
说明理由.
(3)解:月销售额可以定为每月18万元(中位数). 理由如下:
因为从样本情况看,月销售额在18万元以上(含18万元)的有16人,占总人数的一半左右,可以估计,
如果月销售额定为18万元,将有一半左右的营业员获得奖励.
众数:15,中位数:18,平均数:20
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}销售额/万元
13
14
15
16
17
18
19
22
23
24
26
28
30
32
人数
1
1
5
4
3
2
3
1
1
1
2
3
1
2
共30人
16人
五、总结凝炼
一种思想
两个公式
四个概念
样本估计总体的统计思想
加权平均数:
加权平均数
方差:
中位数
众数
方差
六、课后作业
归纳
1.某中学“环保小组”的5名同学在一次活动中捡废弃塑料袋的个数分别是
4, 6,8,8,10,这组数据的众数为( )
A. 4 B. 6 C. 8 D. 10
2. 某校5名同学在“国学经典诵读”比赛中,成绩(单位:分)分别是86,95,
97,90,88,这组数据的中位数是( )
A. 97 B. 90 C. 95 D. 88
3. 若一组数据1,2,3,n的平均数是2,则这组数据的方差为( )
A. 1 B. 2 C. 3 D.
C
B
D
六、课后作业
归纳
4. 甲、乙两人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为 =0.63, =0.51,则两人中成绩最稳定的是( )
A. 甲 B. 乙 C. 一样 D. 不确定
5. 宁宁所在的班级有42人,某次考试他的成绩是80分,若全班同学的平均分是78分,判断宁宁的成绩是否在班级属于中等偏上,还需要了解班级成绩的( )
A. 中位数 B. 众数 C. 加权平均数 D. 方差
B
A
六、课后作业
6. (2019云南)某公司销售部有营业员15人,该公司为了调动营业员的积极性,决定实行目标管理,根据目标完成的情况对营业员进行适当的奖励,为了确定一个适当的月销售目标,公司有关部门统计了这15人某月的销售量,如下表所示:
{5940675A-B579-460E-94D1-54222C63F5DA}月销售量/件数
1770
480
220
180
120
90
人数
1
1
3
3
3
4
(1)直接写出这15名营业员该月销售量数据的平均数、中位数、众数;
(2)如果想让一半左右的营业员都能达到月销售目标,你认为(1)中的平均数、中位数、
众数中,哪个最适合作为月销售目标?请说明理由.
六、课后作业
解:(1)这15名营业员该月销售量数据的平均数为278件, 中位数为180件,众数为90件;
【解法提示】平均数x= ×(1770+480+220×3+180×3+120×3+90×4)=278(件) ;把这15个数据按从大到小顺的序排列,位于第8个位置的数据是180,∴中位数是180件;在这15个数据中,数据90出现了4次,为出现次数最多的数据,∴众数是90件.
(2)中位数最适合作为销售目标.理由如下:
在这15人中,月销售额不低于278(平均数)件的有2人,月销售额不低于180(中位数)件的有8人,月销售额不低于90(众数)件的有15人.∴如果想让一半左右的营业员都能够达到月销售目标,(1)中的平均数、中位数、众数中,中位数最适合作为月销售目标.
