人教版八年级数学下册 第十九章《一次函数》复习(1) 课件(共16张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第十九章《一次函数》复习(1) 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 860.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览


文档简介
第十九章
《一次函数》复习(1)
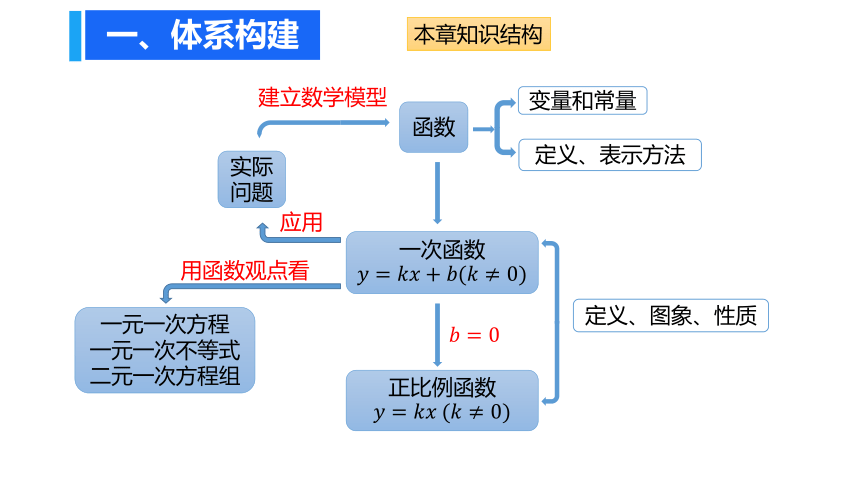
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
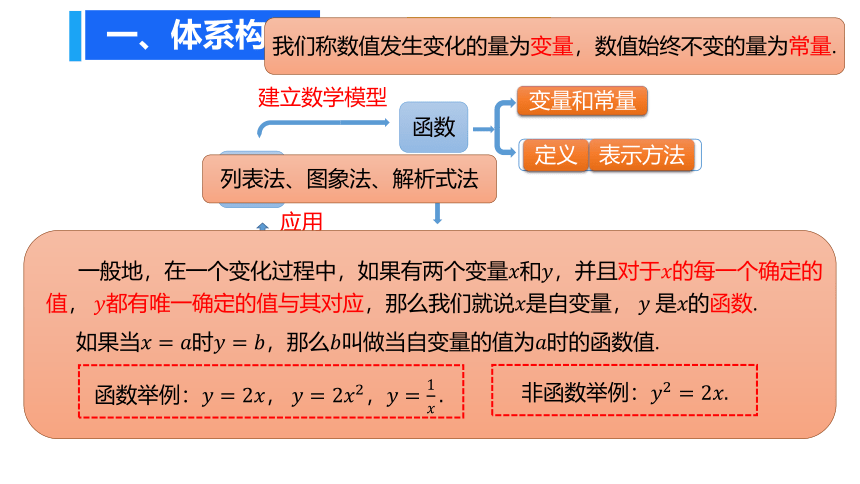
变量和常量
我们称数值发生变化的量为变量,数值始终不变的量为常量.
一般地,在一个变化过程中,如果有两个变量????和????,并且对于????的每一个确定的值, ????都有唯一确定的值与其对应,那么我们就说????是自变量, ???? 是????的函数.
?
如果当????=????时????=????,那么????叫做当自变量的值为????时的函数值.
?
定义
表示方法
函数举例:????=2????, ????=2????2,????=1????.
?
非函数举例:????2=2????.
?
列表法、图象法、解析式法
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
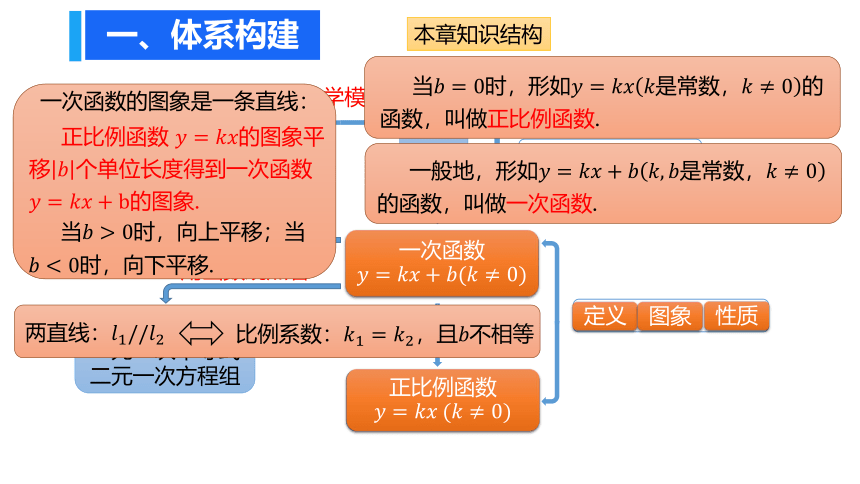
一般地,形如????=????????+????????,????是常数,????≠0的函数,叫做一次函数.
?
当????=0时,形如????=????????????是常数,????≠0的函数,叫做正比例函数.
?
一次函数
????=????????+????(????≠0)
?
正比例函数
????=?????????(????≠0)
?
定义
图象
一次函数的图象是一条直线:
正比例函数 ????=????????的图象平移????个单位长度得到一次函数 ????=????????+b的图象.
?
当????>0时,向上平移;当????<0时,向下平移.
?
两直线:????1//????2
?
比例系数:????1=????2,且????不相等
?
性质
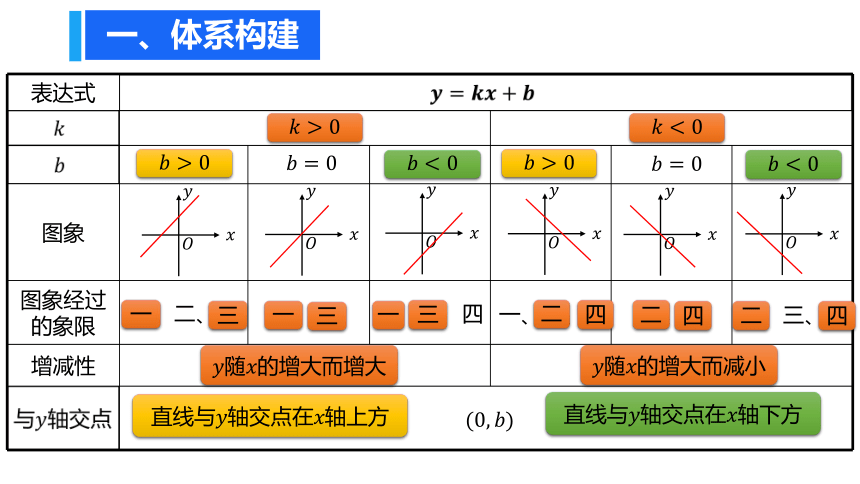
一、体系构建
{5940675A-B579-460E-94D1-54222C63F5DA}表达式
图象
图象经过
的象限
增减性
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????>0
?
????<0
?
????>0
?
????=0
?
????<0
?
????>0
?
????=0
?
????<0
?
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
????随????的增大而增大
?
????随????的增大而减小
?
(0,????)
?
????>0
?
????随????的增大而增大
?
????随????的增大而减小
?
????<0
?
????>0
?
????>0
?
直线与????轴交点在????轴上方
?
????<0
?
????<0
?
直线与????轴交点在????轴下方
?
一
一
一
二
二
二
四
四
四
三
三
三
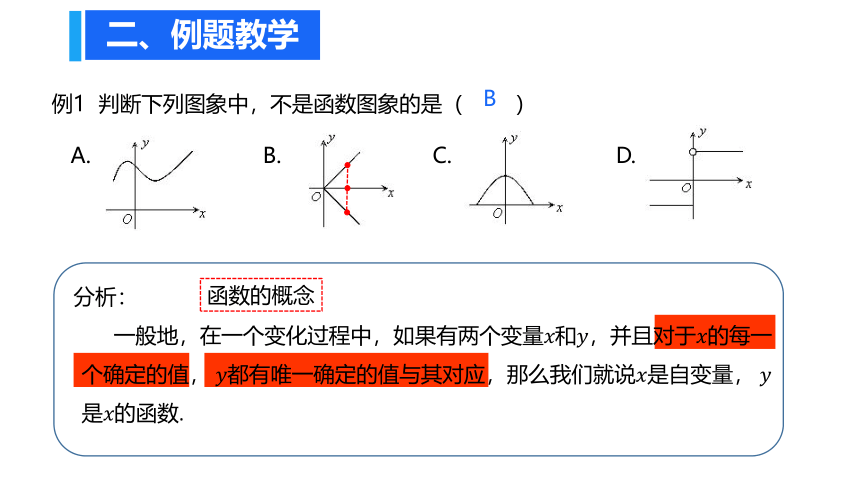
例1 判断下列图象中,不是函数图象的是( )
A. B. ?C. ?D.
?
二、例题教学
B
分析:
一般地,在一个变化过程中,如果有两个变量????和????,并且对于????的每一个确定的值, ????都有唯一确定的值与其对应,那么我们就说????是自变量, ???? 是????的函数.
?
函数的概念
二、例题教学
一般地,形如????=????????????是常数,????≠0的函数,叫做正比例函数.
?
例2 下列函数中是正比例函数的是( )
A.????=?8???? B.????=?8???? C.????=5????2+6 D.????=?0.5?????1
?
A
例3 正比例函数????=2????经过第 象限,????随????的增大而 .
?
一、三
增大
分析:
∵正比例函数????=2????的图象是一条直线,且????>0,
?
????
?
????
?
????
?
∴函数????=2????的大致图象如图,
?
∴函数????=2????经过第一象限和第三象限,
?
????随????的增大而增大.
?
画出大致图象
三、方法迁移
分析:
变式1.1 如果????=?????1????1?????2+3是一次函数,则????的值是( )
A.±1 B.1 C.?1 D.无法确定
?
C
变式1.2 如果????=????1?????2+?????1是正比例函数,则????的值是( )
A.±1 B.1 C.?1 D.无法确定
?
∵????=?????1????1?????2+3是一次函数,
?
∴?????1≠01?????2=1,
?
解得????≠1????=±1,
?
∴ ????=?1.
?
B
分析:
∴1?????2=1?????1=0,
?
解得????=±1????=1,
?
∴ ????=1.
?
????=????????+????????,????是常数,????≠0
?
????=????????????是常数,????≠0
?
∵????=????1?????2+?????1是正比例函数,
?
三、方法迁移
分析:
变式2.1 正比例函数????=2????向上平移3个单位长度得到的一次函数不经过第 象限, ????随????的增大而 .
?
∵ ????=2????
?
向上平移3个单位长度
????=2????+3
?
∴函数????=2????+3的大致图象如图2,
?
∴函数????=2????+3不经过第四象限,
?
????随????的增大而增大.
?
????
?
????
?
????
?
图1
????
?
????
?
????
?
图2
画出大致图象
四
增大
三、方法迁移
分析:
变式2.2 函数????=????????+3不经过第四象限,则????的取值范围为 .
?
∴函数????=????????+3的可能的大致图象如图,
?
∵函数????=????????+3的????>0,
?
∴ ????的取值范围为:????>0.
?
????
?
????
?
????
?
????>0
?
????
?
????
?
????
?
????<0
?
∵函数????=????????+3不经过第四象限,
?
画出大致图象
????>0
?
四、思维提升
一次函数:形如????=????????+????
?
要求:????≠0未知数的次数为1
?
一次函数的概念题型解题关键
正比例函数:形如????=????????+????
?
一次函数的图象和性质解题关键
要求:????≠0????=0未知数的次数为1
?
1
1
画出大致图象
????
?
????>0,????随????的增大而增大
?
????<0,????随????的增大而减小
?
????
?
b>0,直线与????轴交点在????轴上方
?
b<0,直线与????轴交点在????轴下方
?
五、总结凝练
归纳
归纳
?
?
二、三、四
减小
六、课后作业
?
①④
①
六、课后作业
?
?
?
一、三
?
?
六、课后作业
归纳
归纳
5. 已知函数????=(1?????)????+????2?1.若它是正比例函数,则????的值为 ;若它是一次函数,则????的取值范围为 .
?
?1
?
????≠1
?
6.已知直线????=????????+1经过一定点,求该定点的坐标为 .
?
(0,1)
?
谢谢观看!
谢谢观看!
《一次函数》复习(1)
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
变量和常量
我们称数值发生变化的量为变量,数值始终不变的量为常量.
一般地,在一个变化过程中,如果有两个变量????和????,并且对于????的每一个确定的值, ????都有唯一确定的值与其对应,那么我们就说????是自变量, ???? 是????的函数.
?
如果当????=????时????=????,那么????叫做当自变量的值为????时的函数值.
?
定义
表示方法
函数举例:????=2????, ????=2????2,????=1????.
?
非函数举例:????2=2????.
?
列表法、图象法、解析式法
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
一般地,形如????=????????+????????,????是常数,????≠0的函数,叫做一次函数.
?
当????=0时,形如????=????????????是常数,????≠0的函数,叫做正比例函数.
?
一次函数
????=????????+????(????≠0)
?
正比例函数
????=?????????(????≠0)
?
定义
图象
一次函数的图象是一条直线:
正比例函数 ????=????????的图象平移????个单位长度得到一次函数 ????=????????+b的图象.
?
当????>0时,向上平移;当????<0时,向下平移.
?
两直线:????1//????2
?
比例系数:????1=????2,且????不相等
?
性质
一、体系构建
{5940675A-B579-460E-94D1-54222C63F5DA}表达式
图象
图象经过
的象限
增减性
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????>0
?
????<0
?
????>0
?
????=0
?
????<0
?
????>0
?
????=0
?
????<0
?
一、二、三
一、三
一、三、四
一、二、四
二、四
二、三、四
????随????的增大而增大
?
????随????的增大而减小
?
(0,????)
?
????>0
?
????随????的增大而增大
?
????随????的增大而减小
?
????<0
?
????>0
?
????>0
?
直线与????轴交点在????轴上方
?
????<0
?
????<0
?
直线与????轴交点在????轴下方
?
一
一
一
二
二
二
四
四
四
三
三
三
例1 判断下列图象中,不是函数图象的是( )
A. B. ?C. ?D.
?
二、例题教学
B
分析:
一般地,在一个变化过程中,如果有两个变量????和????,并且对于????的每一个确定的值, ????都有唯一确定的值与其对应,那么我们就说????是自变量, ???? 是????的函数.
?
函数的概念
二、例题教学
一般地,形如????=????????????是常数,????≠0的函数,叫做正比例函数.
?
例2 下列函数中是正比例函数的是( )
A.????=?8???? B.????=?8???? C.????=5????2+6 D.????=?0.5?????1
?
A
例3 正比例函数????=2????经过第 象限,????随????的增大而 .
?
一、三
增大
分析:
∵正比例函数????=2????的图象是一条直线,且????>0,
?
????
?
????
?
????
?
∴函数????=2????的大致图象如图,
?
∴函数????=2????经过第一象限和第三象限,
?
????随????的增大而增大.
?
画出大致图象
三、方法迁移
分析:
变式1.1 如果????=?????1????1?????2+3是一次函数,则????的值是( )
A.±1 B.1 C.?1 D.无法确定
?
C
变式1.2 如果????=????1?????2+?????1是正比例函数,则????的值是( )
A.±1 B.1 C.?1 D.无法确定
?
∵????=?????1????1?????2+3是一次函数,
?
∴?????1≠01?????2=1,
?
解得????≠1????=±1,
?
∴ ????=?1.
?
B
分析:
∴1?????2=1?????1=0,
?
解得????=±1????=1,
?
∴ ????=1.
?
????=????????+????????,????是常数,????≠0
?
????=????????????是常数,????≠0
?
∵????=????1?????2+?????1是正比例函数,
?
三、方法迁移
分析:
变式2.1 正比例函数????=2????向上平移3个单位长度得到的一次函数不经过第 象限, ????随????的增大而 .
?
∵ ????=2????
?
向上平移3个单位长度
????=2????+3
?
∴函数????=2????+3的大致图象如图2,
?
∴函数????=2????+3不经过第四象限,
?
????随????的增大而增大.
?
????
?
????
?
????
?
图1
????
?
????
?
????
?
图2
画出大致图象
四
增大
三、方法迁移
分析:
变式2.2 函数????=????????+3不经过第四象限,则????的取值范围为 .
?
∴函数????=????????+3的可能的大致图象如图,
?
∵函数????=????????+3的????>0,
?
∴ ????的取值范围为:????>0.
?
????
?
????
?
????
?
????>0
?
????
?
????
?
????
?
????<0
?
∵函数????=????????+3不经过第四象限,
?
画出大致图象
????>0
?
四、思维提升
一次函数:形如????=????????+????
?
要求:????≠0未知数的次数为1
?
一次函数的概念题型解题关键
正比例函数:形如????=????????+????
?
一次函数的图象和性质解题关键
要求:????≠0????=0未知数的次数为1
?
1
1
画出大致图象
????
?
????>0,????随????的增大而增大
?
????<0,????随????的增大而减小
?
????
?
b>0,直线与????轴交点在????轴上方
?
b<0,直线与????轴交点在????轴下方
?
五、总结凝练
归纳
归纳
?
?
二、三、四
减小
六、课后作业
?
①④
①
六、课后作业
?
?
?
一、三
?
?
六、课后作业
归纳
归纳
5. 已知函数????=(1?????)????+????2?1.若它是正比例函数,则????的值为 ;若它是一次函数,则????的取值范围为 .
?
?1
?
????≠1
?
6.已知直线????=????????+1经过一定点,求该定点的坐标为 .
?
(0,1)
?
谢谢观看!
谢谢观看!
