人教版八年级数学下册 第十九章《一次函数》复习(2)课件(共17张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第十九章《一次函数》复习(2)课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 866.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:14:29 | ||
图片预览


文档简介
第十九章
《一次函数》复习(2)
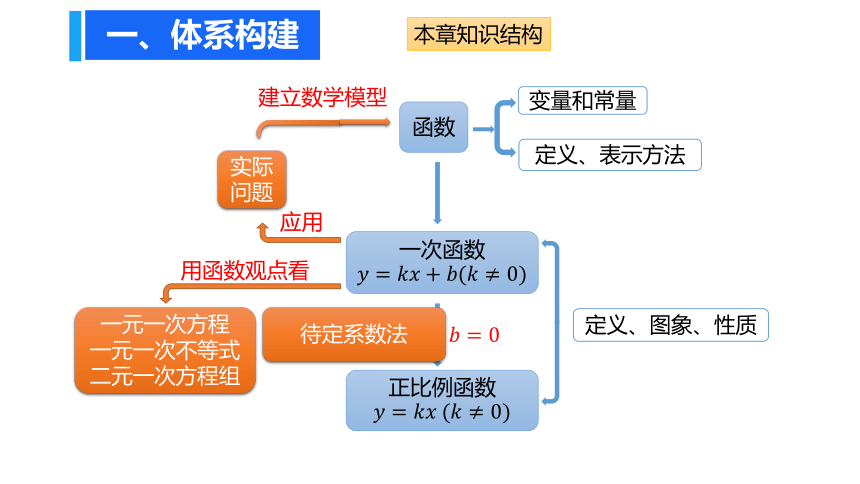
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
待定系数法
二、例题教学
例1 已知一次函数的图象如图,经过点A(1,3)和点????(?1,?1),求该一次函数的解析式.
?
解:设该一次函数解析式为:????=????????+????,
?
∵函数图象经过点A(1,3)和????(?1,?1),
?
∴????+????=3?????+????=?1,
?
∴????=2????=1,
?
∴该一次函数解析式为:????=2????+1.
?
①设
②代
③解
?
④得
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
待定系数法
二、例题教学
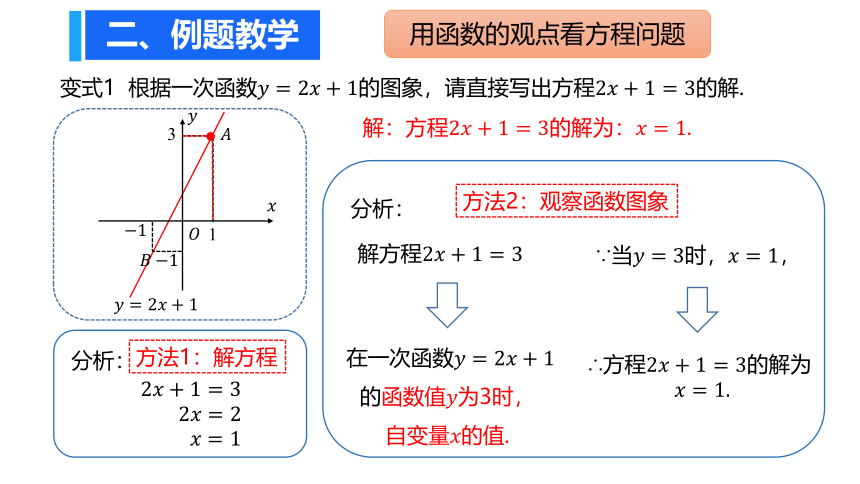
变式1 根据一次函数????=2????+1的图象,请直接写出方程2????+1=3的解.
?
分析:
在一次函数????=2????+1
的函数值????为3时,
自变量????的值.
?
∵当????=3时,????=1,
?
∴方程2????+1=3的解为
????=1.
?
解方程2????+1=3
?
解:方程2????+1=3的解为:????=1.
?
分析:
2????+1=3
?
方法1:解方程
2????=2
?
????=1
?
方法2:观察函数图象
用函数的观点看方程问题
????=2????+1
?
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
二、例题教学
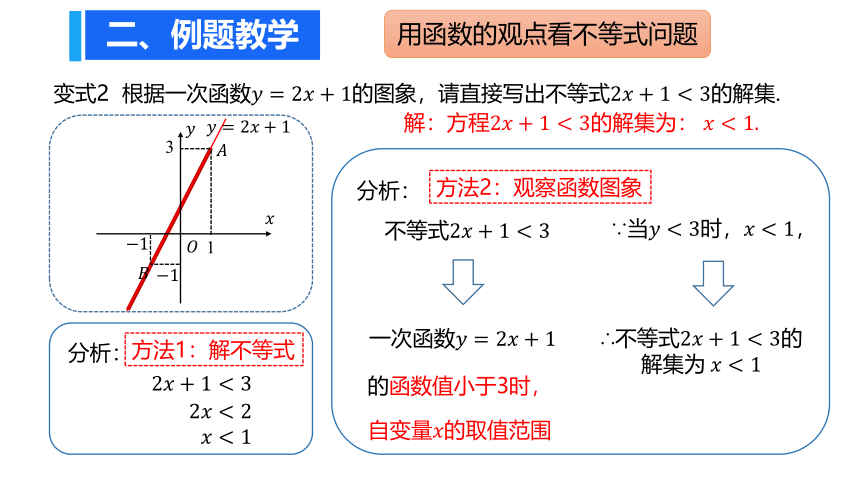
变式2 根据一次函数????=2????+1的图象,请直接写出不等式2????+1<3的解集.
?
分析:
一次函数????=2????+1
的函数值小于3时,
自变量????的取值范围
?
∵当????<3时,????<1,
?
∴不等式2????+1<3的
解集为 ????<1
?
不等式2????+1<3
?
解:方程2????+1<3的解集为: ????<1.
?
分析:
2????+1<3
?
方法1:解不等式
2????<2
?
????<1
?
方法2:观察函数图象
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
????=2????+1
?
用函数的观点看不等式问题
二、例题教学
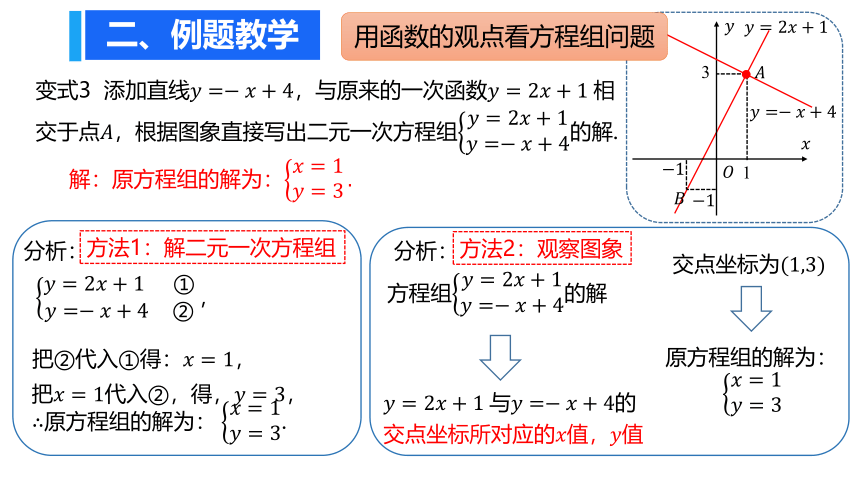
变式3 添加直线????=?????+4,与原来的一次函数????=2????+1?相交于点????,根据图象直接写出二元一次方程组????=2????+1????=?????+4的解.
?
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
分析:
解:原方程组的解为:????=1????=3.
?
????=?????+4
?
方法2:观察图象
∴原方程组的解为: ????=1????=3.
?
分析:
方法1:解二元一次方程组
????=2????+1??????①????=?????+4?????②,
?
把②代入①得:????=1,
?
把????=1代入②,得,????=3,
?
方程组????=2????+1????=?????+4的解
?
????=2????+1?与????=?????+4的
交点坐标所对应的????值,????值
?
交点坐标为(1,3)
?
原方程组的解为:
????=1????=3
?
????=2????+1
?
用函数的观点看方程组问题
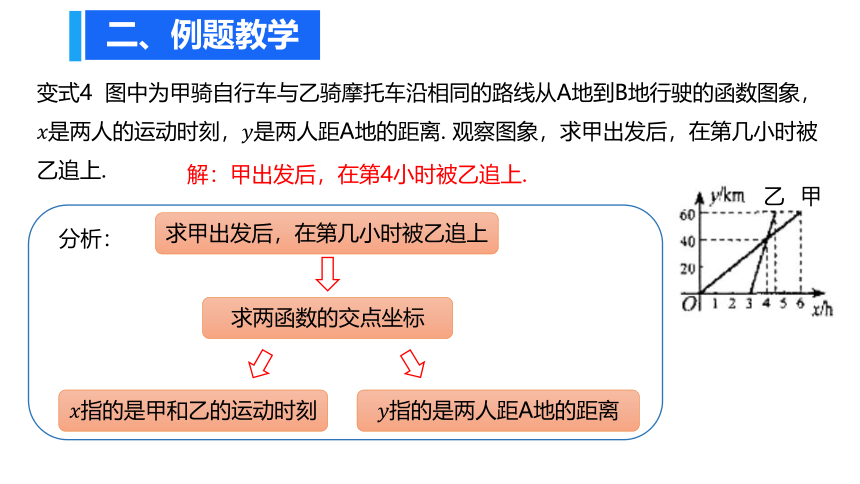
变式4 图中为甲骑自行车与乙骑摩托车沿相同的路线从A地到B地行驶的函数图象,????是两人的运动时刻,????是两人距A地的距离. 观察图象,求甲出发后,在第几小时被乙追上.
?
二、例题教学
解:甲出发后,在第4小时被乙追上.
分析:
求甲出发后,在第几小时被乙追上
求两函数的交点坐标
甲
乙
????指的是甲和乙的运动时刻
?
????指的是两人距A地的距离
?
三、方法迁移
2. 已知,直线????=2????+3与直线????=?2?????1.
(1)求两直线交点????的坐标;
?
求两直线交点坐标
求方程组的解
????=?1????=1,
?
解得:
解:
????=2????+3????=?2?????1 ,
?
联立方程组:
∴交点????的坐标为(?1,1).
?
分析:
????=2????+3
?
????=?2?????1
?
三、方法迁移
2. 已知,直线????=2????+3与直线????=?2?????1.
(2)求?????????????的面积;
?
求?????????????的面积
?
求底AB的长,
作高并求高CD的长.
当????=0时,
?
分析:
????=12?????????????????
?
求点????、????、????的坐标
?
????=0+3=3,
?
????=0?1=?1,
?
∴????(0,3), ????0,?1,
?
∴????????=4.
?
∵????(?1,1),
?
∴????????=1,
?
解:
过点????作????????⊥????????交????????于点????,
?
∴????=12?????????????????,
?
=12×4×1,
?
=2.
?
∴?????????????的面积为2.
?
D
????=2????+3
?
????=?2?????1
?
三、方法迁移
2. 已知,直线????=2????+3与直线????=?2?????1.
(3)观察图象,直接写出不等式2????+3>?2?????1的解集.
?
分析:
解:不等式2????+3>?2?????1的解集为: ????>?1.
?
求不等式2????+3>?2?????1的解集
?
函数????1=2????+3与函数????2=?2?????1中,当????1> ????2时,求 ????的取值范围
?
方法1:解不等式
方法2:观察图象
????=2????+3
?
????=?2?????1
?
(?1,1)
?
四、思维提升
第一步 设一次函数(直线)解析式为:????=????????+????;
?
待定系数法求函数解析式
用函数观点看方程(组)和不等式
1.解方程:????????+????=????
?
,即求纵坐标为????时,对应的点的横坐标的值.
?
第二步 把两个点的坐标代入函数解析式;
第三步 解二元一次方程组;
第四步 下结论,写出函数解析式.
①设
②代
③解
?
④得
2.解不等式:????????+????>????
?
,即求函数纵坐标大于????时,对应的点的横坐标取值范围.
?
3.解方程组:
????1????+????1=????1????2????+????2=????2
?
,即求函数????1=????1????+????1与????2=????2????+????2的交点坐标.
?
五、总结凝练
归纳
归纳
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
2.已知一次函数????=????????+????(????≠0),????,????的部分对应值如下表,求关于方程????????+?????=0的解是 .
3.若直线????=????????+????与????轴交于点(2,0),则关于????的不等式?????+????>0的解集是 .
4.一次函数????=2????+6与????=?2?????2的图象交于点(?2,2),求方程组
的解为 .
5.一个弹簧不挂重物时长12????????,挂上重物后伸长的长度与所挂重物的质量成正比.如
果挂上1????????的物体后,弹簧伸长2????????.求弹簧总长????(单位:????????)关于所挂物体质量
????????(单位:????????)的函数解析式.
?
{5940675A-B579-460E-94D1-54222C63F5DA}x
y
????=2????+6????=?2?????2
?
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
?
解:由题意得:
2????+????=4?2????+????=?2,解得:????=32????=1,
∴????的值为32, ????的值为1.
?
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
2.已知一次函数????=????????+????(????≠0),????,????的部分对应值如下表,求关于方程????????+?????=0的解是 .
3.若直线????=????????+????与????轴交于点(2,0),则关于????的不等式?????+????>0的解集是 .
4.一次函数????=2????+6与????=?2?????2的图象交于点(?2,2),求方程组
的解为 .
5.一个弹簧不挂重物时长12????????,挂上重物后伸长的长度与所挂重物的质量成正比.如
果挂上1????????的物体后,弹簧伸长2????????.求弹簧总长????(单位:????????)关于所挂物体质量
????????(单位:????????)的函数解析式.
?
{5940675A-B579-460E-94D1-54222C63F5DA}x
y
????=2????+6????=?2?????2
?
????=2
?
????<2
?
????=?2????=2
?
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
?
解:由题意得:
2????+????=4?2????+????=?2,解得:????=32????=1,
∴????的值为32, ????的值为1.
?
5.一个弹簧不挂重物时长12????????,挂上重物后伸长的长度与所挂重物的质量成正比.如
果挂上1????????的物体后,弹簧伸长2????????.求弹簧总长????(单位:????????)关于所挂物体质量
????????(单位:????????)的函数解析式.
?
解:设函数解析式为:????=????????+????,
????=12????+????=12+2,解得:????=2????=12,
∴弹簧总长关于所挂物体质量的函数解析式为:????=2????+12.
?
谢谢倾听
《一次函数》复习(2)
一、体系构建
本章知识结构
函数
变量和常量
定义、表示方法
一次函数
????=????????+????(????≠0)
?
一元一次方程
一元一次不等式
二元一次方程组
实际问题
应用
建立数学模型
定义、图象、性质
正比例函数
????=?????????(????≠0)
?
????=0
?
用函数观点看
待定系数法
二、例题教学
例1 已知一次函数的图象如图,经过点A(1,3)和点????(?1,?1),求该一次函数的解析式.
?
解:设该一次函数解析式为:????=????????+????,
?
∵函数图象经过点A(1,3)和????(?1,?1),
?
∴????+????=3?????+????=?1,
?
∴????=2????=1,
?
∴该一次函数解析式为:????=2????+1.
?
①设
②代
③解
?
④得
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
待定系数法
二、例题教学
变式1 根据一次函数????=2????+1的图象,请直接写出方程2????+1=3的解.
?
分析:
在一次函数????=2????+1
的函数值????为3时,
自变量????的值.
?
∵当????=3时,????=1,
?
∴方程2????+1=3的解为
????=1.
?
解方程2????+1=3
?
解:方程2????+1=3的解为:????=1.
?
分析:
2????+1=3
?
方法1:解方程
2????=2
?
????=1
?
方法2:观察函数图象
用函数的观点看方程问题
????=2????+1
?
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
二、例题教学
变式2 根据一次函数????=2????+1的图象,请直接写出不等式2????+1<3的解集.
?
分析:
一次函数????=2????+1
的函数值小于3时,
自变量????的取值范围
?
∵当????<3时,????<1,
?
∴不等式2????+1<3的
解集为 ????<1
?
不等式2????+1<3
?
解:方程2????+1<3的解集为: ????<1.
?
分析:
2????+1<3
?
方法1:解不等式
2????<2
?
????<1
?
方法2:观察函数图象
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
????=2????+1
?
用函数的观点看不等式问题
二、例题教学
变式3 添加直线????=?????+4,与原来的一次函数????=2????+1?相交于点????,根据图象直接写出二元一次方程组????=2????+1????=?????+4的解.
?
????
?
????
?
????
?
????
?
????
?
1
?1
?
?1
?
3
分析:
解:原方程组的解为:????=1????=3.
?
????=?????+4
?
方法2:观察图象
∴原方程组的解为: ????=1????=3.
?
分析:
方法1:解二元一次方程组
????=2????+1??????①????=?????+4?????②,
?
把②代入①得:????=1,
?
把????=1代入②,得,????=3,
?
方程组????=2????+1????=?????+4的解
?
????=2????+1?与????=?????+4的
交点坐标所对应的????值,????值
?
交点坐标为(1,3)
?
原方程组的解为:
????=1????=3
?
????=2????+1
?
用函数的观点看方程组问题
变式4 图中为甲骑自行车与乙骑摩托车沿相同的路线从A地到B地行驶的函数图象,????是两人的运动时刻,????是两人距A地的距离. 观察图象,求甲出发后,在第几小时被乙追上.
?
二、例题教学
解:甲出发后,在第4小时被乙追上.
分析:
求甲出发后,在第几小时被乙追上
求两函数的交点坐标
甲
乙
????指的是甲和乙的运动时刻
?
????指的是两人距A地的距离
?
三、方法迁移
2. 已知,直线????=2????+3与直线????=?2?????1.
(1)求两直线交点????的坐标;
?
求两直线交点坐标
求方程组的解
????=?1????=1,
?
解得:
解:
????=2????+3????=?2?????1 ,
?
联立方程组:
∴交点????的坐标为(?1,1).
?
分析:
????=2????+3
?
????=?2?????1
?
三、方法迁移
2. 已知,直线????=2????+3与直线????=?2?????1.
(2)求?????????????的面积;
?
求?????????????的面积
?
求底AB的长,
作高并求高CD的长.
当????=0时,
?
分析:
????=12?????????????????
?
求点????、????、????的坐标
?
????=0+3=3,
?
????=0?1=?1,
?
∴????(0,3), ????0,?1,
?
∴????????=4.
?
∵????(?1,1),
?
∴????????=1,
?
解:
过点????作????????⊥????????交????????于点????,
?
∴????=12?????????????????,
?
=12×4×1,
?
=2.
?
∴?????????????的面积为2.
?
D
????=2????+3
?
????=?2?????1
?
三、方法迁移
2. 已知,直线????=2????+3与直线????=?2?????1.
(3)观察图象,直接写出不等式2????+3>?2?????1的解集.
?
分析:
解:不等式2????+3>?2?????1的解集为: ????>?1.
?
求不等式2????+3>?2?????1的解集
?
函数????1=2????+3与函数????2=?2?????1中,当????1> ????2时,求 ????的取值范围
?
方法1:解不等式
方法2:观察图象
????=2????+3
?
????=?2?????1
?
(?1,1)
?
四、思维提升
第一步 设一次函数(直线)解析式为:????=????????+????;
?
待定系数法求函数解析式
用函数观点看方程(组)和不等式
1.解方程:????????+????=????
?
,即求纵坐标为????时,对应的点的横坐标的值.
?
第二步 把两个点的坐标代入函数解析式;
第三步 解二元一次方程组;
第四步 下结论,写出函数解析式.
①设
②代
③解
?
④得
2.解不等式:????????+????>????
?
,即求函数纵坐标大于????时,对应的点的横坐标取值范围.
?
3.解方程组:
????1????+????1=????1????2????+????2=????2
?
,即求函数????1=????1????+????1与????2=????2????+????2的交点坐标.
?
五、总结凝练
归纳
归纳
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
2.已知一次函数????=????????+????(????≠0),????,????的部分对应值如下表,求关于方程????????+?????=0的解是 .
3.若直线????=????????+????与????轴交于点(2,0),则关于????的不等式?????+????>0的解集是 .
4.一次函数????=2????+6与????=?2?????2的图象交于点(?2,2),求方程组
的解为 .
5.一个弹簧不挂重物时长12????????,挂上重物后伸长的长度与所挂重物的质量成正比.如
果挂上1????????的物体后,弹簧伸长2????????.求弹簧总长????(单位:????????)关于所挂物体质量
????????(单位:????????)的函数解析式.
?
{5940675A-B579-460E-94D1-54222C63F5DA}x
y
????=2????+6????=?2?????2
?
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
?
解:由题意得:
2????+????=4?2????+????=?2,解得:????=32????=1,
∴????的值为32, ????的值为1.
?
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
2.已知一次函数????=????????+????(????≠0),????,????的部分对应值如下表,求关于方程????????+?????=0的解是 .
3.若直线????=????????+????与????轴交于点(2,0),则关于????的不等式?????+????>0的解集是 .
4.一次函数????=2????+6与????=?2?????2的图象交于点(?2,2),求方程组
的解为 .
5.一个弹簧不挂重物时长12????????,挂上重物后伸长的长度与所挂重物的质量成正比.如
果挂上1????????的物体后,弹簧伸长2????????.求弹簧总长????(单位:????????)关于所挂物体质量
????????(单位:????????)的函数解析式.
?
{5940675A-B579-460E-94D1-54222C63F5DA}x
y
????=2????+6????=?2?????2
?
????=2
?
????<2
?
????=?2????=2
?
六、课后作业
1.已知一次函数????=????????+????,当????=2时????的值为4,当????=?2时????的值为?2,求????与????.
?
解:由题意得:
2????+????=4?2????+????=?2,解得:????=32????=1,
∴????的值为32, ????的值为1.
?
5.一个弹簧不挂重物时长12????????,挂上重物后伸长的长度与所挂重物的质量成正比.如
果挂上1????????的物体后,弹簧伸长2????????.求弹簧总长????(单位:????????)关于所挂物体质量
????????(单位:????????)的函数解析式.
?
解:设函数解析式为:????=????????+????,
????=12????+????=12+2,解得:????=2????=12,
∴弹簧总长关于所挂物体质量的函数解析式为:????=2????+12.
?
谢谢倾听
