人教版八年级数学下册 第十七章《勾股定理》复习 (2)课件(共19张PPT)
文档属性
| 名称 | 人教版八年级数学下册 第十七章《勾股定理》复习 (2)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 461.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:14:44 | ||
图片预览

文档简介
人教版八年级下册
第十七章
《勾股定理》复习(2)
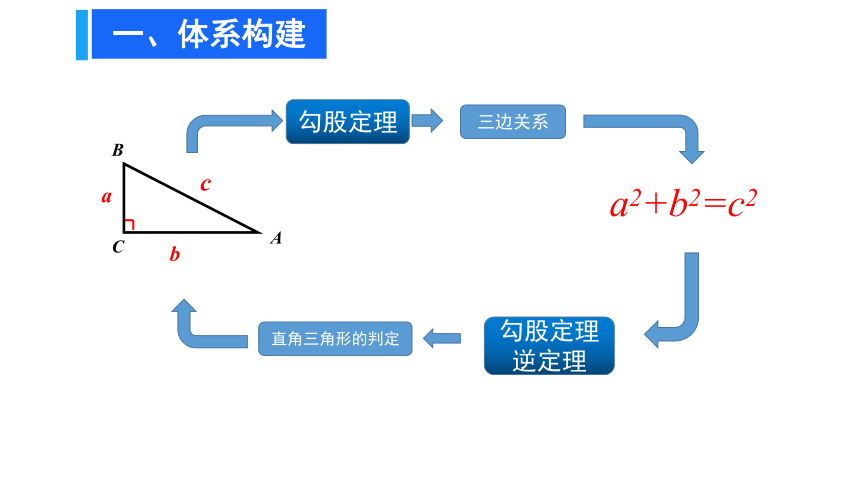
一、体系构建
A
B
C
a
b
c
a2+b2=c2
三边关系
勾股定理逆定理
勾股定理
直角三角形的判定
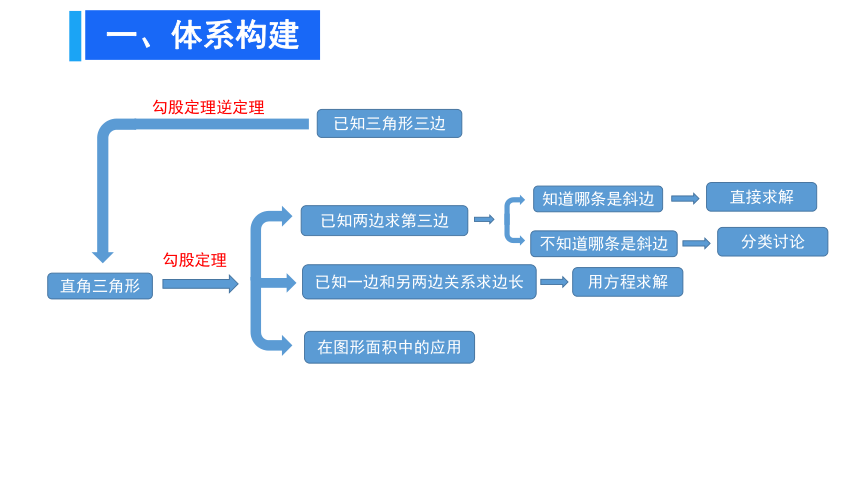
一、体系构建
勾股定理
直角三角形
已知两边求第三边
已知一边和另两边关系求边长
在图形面积中的应用
已知三角形三边
用方程求解
知道哪条是斜边
不知道哪条是斜边
直接求解
分类讨论
勾股定理逆定理
二、例题教学
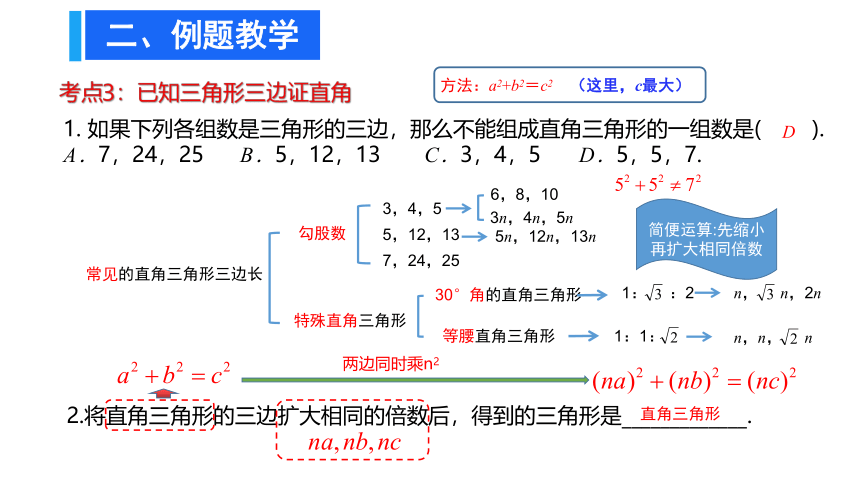
考点3:已知三角形三边证直角
1. 如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( ).
A.7,24,25 B.5,12,13 C.3,4,5 D.5,5,7.
常见的直角三角形三边长
勾股数
特殊直角三角形
30°角的直角三角形
等腰直角三角形
1: :2
1:1:
3,4,5
5,12,13
7,24,25
2.将直角三角形的三边扩大相同的倍数后,得到的三角形是_____________.
直角三角形
6,8,10
3n,4n,5n
5n,12n,13n
n, n,2n
n,n, n
方法:a2+b2=c2 (这里,c最大)
D
简便运算:先缩小再扩大相同倍数
两边同时乘n2
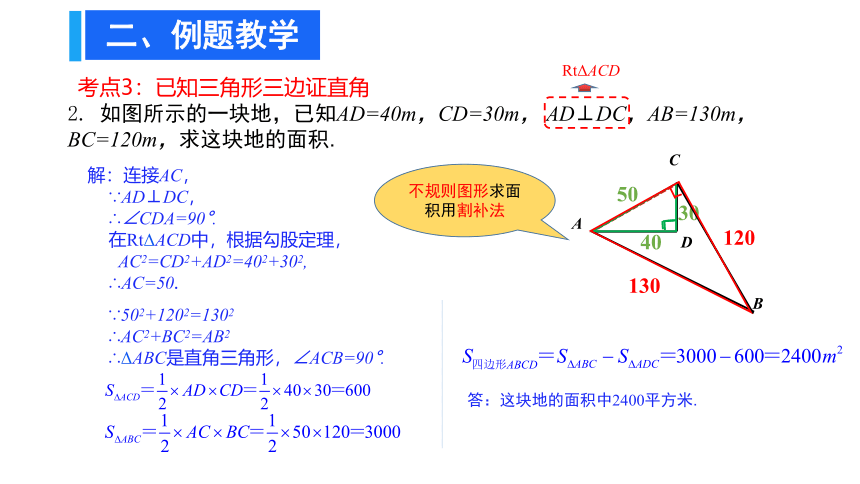
二、例题教学
∵502+1202=1302
∴AC2+BC2=AB2
∴ΔABC是直角三角形,∠ACB=90°.
解:连接AC,
∵AD⊥DC,
∴∠CDA=90°.
在RtΔACD中,根据勾股定理,
AC2=CD2+AD2=402+302,
∴AC=50.
40
120
130
30
50
2. 如图所示的一块地,已知AD=40m,CD=30m, AD⊥DC,AB=130m,BC=120m,求这块地的面积.
A
D
C
B
考点3:已知三角形三边证直角
答:这块地的面积中2400平方米.
RtΔACD
不规则图形求面积用割补法
二、例题教学
考点4:在图形面积中的应用
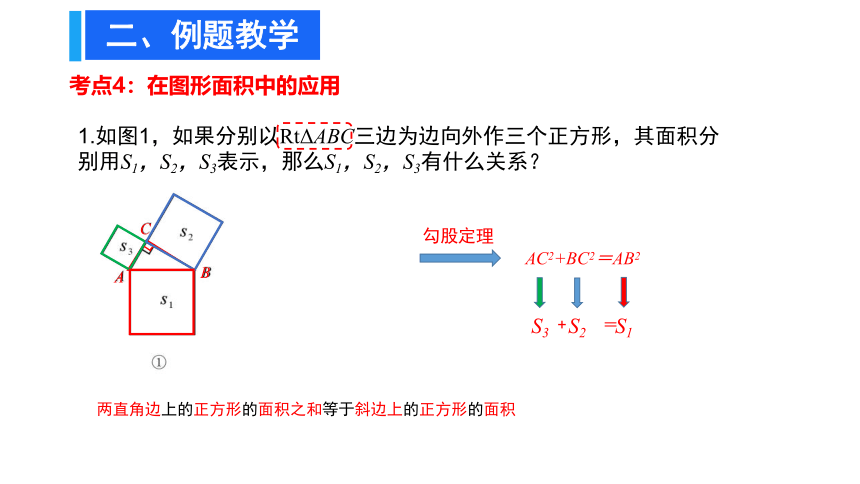
1.如图1,如果分别以RtΔABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3有什么关系?
A
B
C
AC2+BC2=AB2
勾股定理
S3
S2
S1
+ =
两直角边上的正方形的面积之和等于斜边上的正方形的面积
二、例题教学
考点4:在图形面积中的应用
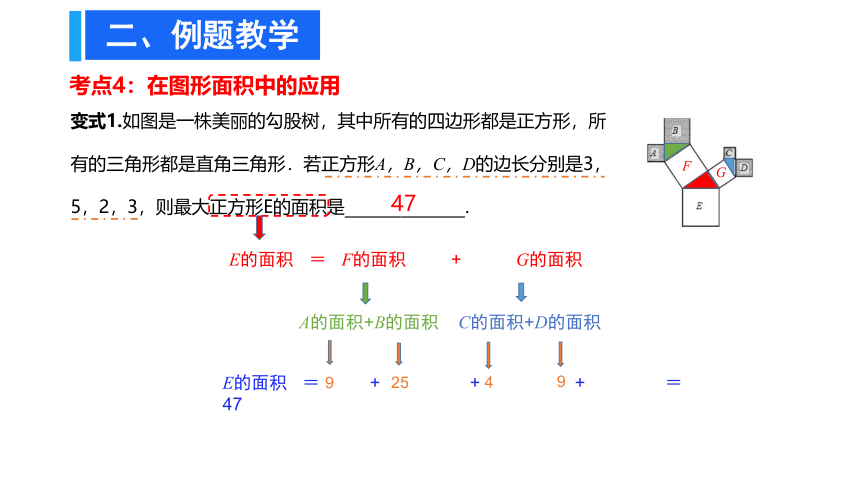
变式1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所
有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,
5,2,3,则最大正方形E的面积是_______________.
F
G
E的面积 = F的面积 + G的面积
A的面积+B的面积
C的面积+D的面积
9
25
4
9
E的面积 = + + + = 47
47
二、例题教学
考点4:在图形面积中的应用
变式2.如图,以ΔABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,已知S1=S2+S3,则ΔABC是直角三角形吗?
AB2
勾股逆定理
ΔABC是直角三角形
BC2
AC2
= +
三、方法迁移
变式3.如图②,分别以RtΔABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,求证:S1=S2+S3 .
A
B
C
AC2+BC2=AB2
勾股定理
两边同时乘以
+ =
S3
S2
S1
三、方法迁移
变式3.如图②,分别以RtΔABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,求证:S1=S2+S3 .
证明:∵
∴
∵在RtΔABC中,有AC2+BC2=AB2
∴
∴ S1=S2+S3.
四、思维提升
变式4. 如图③,分别以RtΔABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
AC2+BC2=AB2
勾股定理
A
B
C
S3
S2
S1
两边同时乘以
E
F
30°
30°
E
F
B
2
1
BF
BF
正三角形面积为
+ =
BF=—AB
1
2
解:S1=S2+S3,理由如下
过E作EF⊥AB于F
在正ΔABE中,AB=BE,AF=BF=
∴
∴
同理得 ,
∵在RtΔABC中,有AC2+BC2=AB2
∴
∴ S1=S2+S3.
四、思维提升
变式4. 如图③,分别以RtΔABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
E
F
五、提炼升华
勾股定理
直角三角形
已知两边求第三边
已知一边和另两边关系求边长
在图形面积中的应用
已知三角形三边
用方程求解
知道哪条是斜边
不知道哪条是斜边
直接求解
分类讨论
勾股定理逆定理
常见的数
简便运算的方法
以直角三角形三边为边
正方形
半圆
等边三角形
?
六、课后作业
1.下列不是一组勾股数的是( ).
A.5,12,13 B. C.12,16,20 D. 7,24,25
4.如图,CD⊥AB于D,AC=9,BC=12,AB=15,你能求CD的长吗?
C
A
D
B
3.已知直角三角形中,
(1)a=9,b=____,c=15 ; (2)a=____,b=40,c=50 ; (3)a=24,b=32,c=________.
2.一个三角形三边分别是5a,12a,13a,则按角分类它是 _______三角形.
六、课后作业
5.分别以RtΔABC三边为底向外作三个等腰直角三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
6.如图,每个小正方形的边长都是1.
(1)求四边形ABCD的周长;
(2)∠BCD是直角吗?
A
B
C
S1
S3
S2
六、课后作业
1.下列不是一组勾股数的是( ).
A.5,12,13 B. C.12,16,20 D. 7,24,25
3.已知直角三角形中,
(1)a=9,b=____ ,c=15; (2)a=____,b=40,c=50 ; (3)a=24,b=32,c=________.
2.一个三角形三边分别是5a,12a,13a,则按角分类它是 _______三角形.
B
直角
12
30
40
解: ∵92+122=152
∴AC2+BC2=AB2
∴ΔABC是直角三角形,∠ACB=90°.
∴
∵AD⊥DC
∴
六、课后作业
归纳
归纳
4.如图,CD⊥AB于D,AC=9,BC=12,AB=15,你能求出CD的长吗?
C
A
D
B
解:S1=S2+S3,理由如下
过D作DE⊥BC于E
在等腰直角ΔABE中,CE=BE=DE
∴
同理得
∵在RtΔABC中,有AC2+BC2=AB2
∴
∴ S1=S2+S3.
六、课后作业
5.分别以RtΔABC三边为底向外作三个等腰直角三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
S1
S3
S2
A
B
C
D
E
六、课后作业
同理得
(2)∠BCD是直角,理由如下:
在ΔBCD中,BC2+CD2=20+5=25=52=BD2
∴ΔBCD是直角三角形,∠BCD是直角.
A
C
D
B
E
F
G
H
I
6.如图,每个小正方形的边长都是1.
(1)求四边形ABCD的周长;
(2)∠BCD是直角吗?
解:如图,连接BD,并定义E,F,G,H,I点
在RtΔABE中
第十七章
《勾股定理》复习(2)
一、体系构建
A
B
C
a
b
c
a2+b2=c2
三边关系
勾股定理逆定理
勾股定理
直角三角形的判定
一、体系构建
勾股定理
直角三角形
已知两边求第三边
已知一边和另两边关系求边长
在图形面积中的应用
已知三角形三边
用方程求解
知道哪条是斜边
不知道哪条是斜边
直接求解
分类讨论
勾股定理逆定理
二、例题教学
考点3:已知三角形三边证直角
1. 如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( ).
A.7,24,25 B.5,12,13 C.3,4,5 D.5,5,7.
常见的直角三角形三边长
勾股数
特殊直角三角形
30°角的直角三角形
等腰直角三角形
1: :2
1:1:
3,4,5
5,12,13
7,24,25
2.将直角三角形的三边扩大相同的倍数后,得到的三角形是_____________.
直角三角形
6,8,10
3n,4n,5n
5n,12n,13n
n, n,2n
n,n, n
方法:a2+b2=c2 (这里,c最大)
D
简便运算:先缩小再扩大相同倍数
两边同时乘n2
二、例题教学
∵502+1202=1302
∴AC2+BC2=AB2
∴ΔABC是直角三角形,∠ACB=90°.
解:连接AC,
∵AD⊥DC,
∴∠CDA=90°.
在RtΔACD中,根据勾股定理,
AC2=CD2+AD2=402+302,
∴AC=50.
40
120
130
30
50
2. 如图所示的一块地,已知AD=40m,CD=30m, AD⊥DC,AB=130m,BC=120m,求这块地的面积.
A
D
C
B
考点3:已知三角形三边证直角
答:这块地的面积中2400平方米.
RtΔACD
不规则图形求面积用割补法
二、例题教学
考点4:在图形面积中的应用
1.如图1,如果分别以RtΔABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3有什么关系?
A
B
C
AC2+BC2=AB2
勾股定理
S3
S2
S1
+ =
两直角边上的正方形的面积之和等于斜边上的正方形的面积
二、例题教学
考点4:在图形面积中的应用
变式1.如图是一株美丽的勾股树,其中所有的四边形都是正方形,所
有的三角形都是直角三角形.若正方形A,B,C,D的边长分别是3,
5,2,3,则最大正方形E的面积是_______________.
F
G
E的面积 = F的面积 + G的面积
A的面积+B的面积
C的面积+D的面积
9
25
4
9
E的面积 = + + + = 47
47
二、例题教学
考点4:在图形面积中的应用
变式2.如图,以ΔABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,已知S1=S2+S3,则ΔABC是直角三角形吗?
AB2
勾股逆定理
ΔABC是直角三角形
BC2
AC2
= +
三、方法迁移
变式3.如图②,分别以RtΔABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,求证:S1=S2+S3 .
A
B
C
AC2+BC2=AB2
勾股定理
两边同时乘以
+ =
S3
S2
S1
三、方法迁移
变式3.如图②,分别以RtΔABC三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,求证:S1=S2+S3 .
证明:∵
∴
∵在RtΔABC中,有AC2+BC2=AB2
∴
∴ S1=S2+S3.
四、思维提升
变式4. 如图③,分别以RtΔABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
AC2+BC2=AB2
勾股定理
A
B
C
S3
S2
S1
两边同时乘以
E
F
30°
30°
E
F
B
2
1
BF
BF
正三角形面积为
+ =
BF=—AB
1
2
解:S1=S2+S3,理由如下
过E作EF⊥AB于F
在正ΔABE中,AB=BE,AF=BF=
∴
∴
同理得 ,
∵在RtΔABC中,有AC2+BC2=AB2
∴
∴ S1=S2+S3.
四、思维提升
变式4. 如图③,分别以RtΔABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
E
F
五、提炼升华
勾股定理
直角三角形
已知两边求第三边
已知一边和另两边关系求边长
在图形面积中的应用
已知三角形三边
用方程求解
知道哪条是斜边
不知道哪条是斜边
直接求解
分类讨论
勾股定理逆定理
常见的数
简便运算的方法
以直角三角形三边为边
正方形
半圆
等边三角形
?
六、课后作业
1.下列不是一组勾股数的是( ).
A.5,12,13 B. C.12,16,20 D. 7,24,25
4.如图,CD⊥AB于D,AC=9,BC=12,AB=15,你能求CD的长吗?
C
A
D
B
3.已知直角三角形中,
(1)a=9,b=____,c=15 ; (2)a=____,b=40,c=50 ; (3)a=24,b=32,c=________.
2.一个三角形三边分别是5a,12a,13a,则按角分类它是 _______三角形.
六、课后作业
5.分别以RtΔABC三边为底向外作三个等腰直角三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
6.如图,每个小正方形的边长都是1.
(1)求四边形ABCD的周长;
(2)∠BCD是直角吗?
A
B
C
S1
S3
S2
六、课后作业
1.下列不是一组勾股数的是( ).
A.5,12,13 B. C.12,16,20 D. 7,24,25
3.已知直角三角形中,
(1)a=9,b=____ ,c=15; (2)a=____,b=40,c=50 ; (3)a=24,b=32,c=________.
2.一个三角形三边分别是5a,12a,13a,则按角分类它是 _______三角形.
B
直角
12
30
40
解: ∵92+122=152
∴AC2+BC2=AB2
∴ΔABC是直角三角形,∠ACB=90°.
∴
∵AD⊥DC
∴
六、课后作业
归纳
归纳
4.如图,CD⊥AB于D,AC=9,BC=12,AB=15,你能求出CD的长吗?
C
A
D
B
解:S1=S2+S3,理由如下
过D作DE⊥BC于E
在等腰直角ΔABE中,CE=BE=DE
∴
同理得
∵在RtΔABC中,有AC2+BC2=AB2
∴
∴ S1=S2+S3.
六、课后作业
5.分别以RtΔABC三边为底向外作三个等腰直角三角形,其面积分别用S1、S2、S3表示,请你确定S1、S2、S3之间的关系并加以证明.
S1
S3
S2
A
B
C
D
E
六、课后作业
同理得
(2)∠BCD是直角,理由如下:
在ΔBCD中,BC2+CD2=20+5=25=52=BD2
∴ΔBCD是直角三角形,∠BCD是直角.
A
C
D
B
E
F
G
H
I
6.如图,每个小正方形的边长都是1.
(1)求四边形ABCD的周长;
(2)∠BCD是直角吗?
解:如图,连接BD,并定义E,F,G,H,I点
在RtΔABE中
