人教版八年级数学下册19.2.2 一次函数(第2课时)课件(共20张PPT)
文档属性
| 名称 | 人教版八年级数学下册19.2.2 一次函数(第2课时)课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 427.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:53:54 | ||
图片预览




文档简介
人教版 八年级数学下册
第19章 一次函数
19.2.2 一次函数(第2课时)
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
y=kx
经过原点的一条直线
一、复习引入
y=kx
图 象
性 质
K>0
y
x
K<0
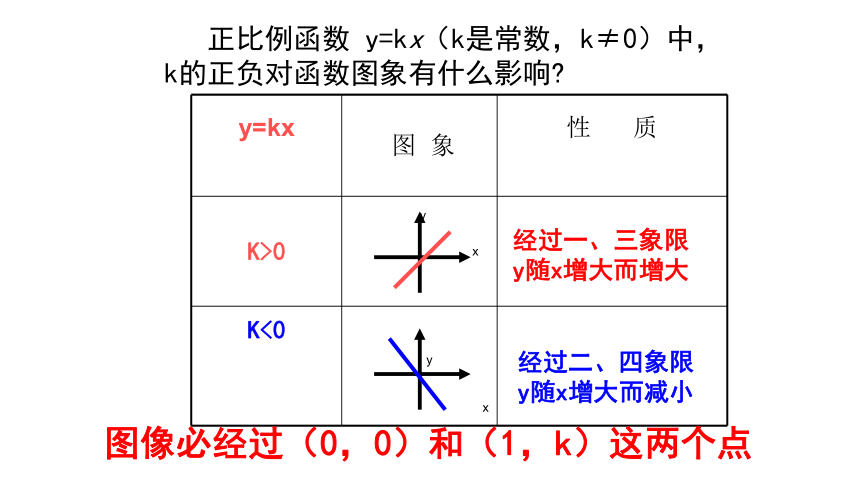
经过一、三象限
y随x增大而增大
经过二、四象限
y随x增大而减小
正比例函数 y=kx(k是常数,k≠0)中,
k的正负对函数图象有什么影响?
y
x
图像必经过(0,0)和(1,k)这两个点
x
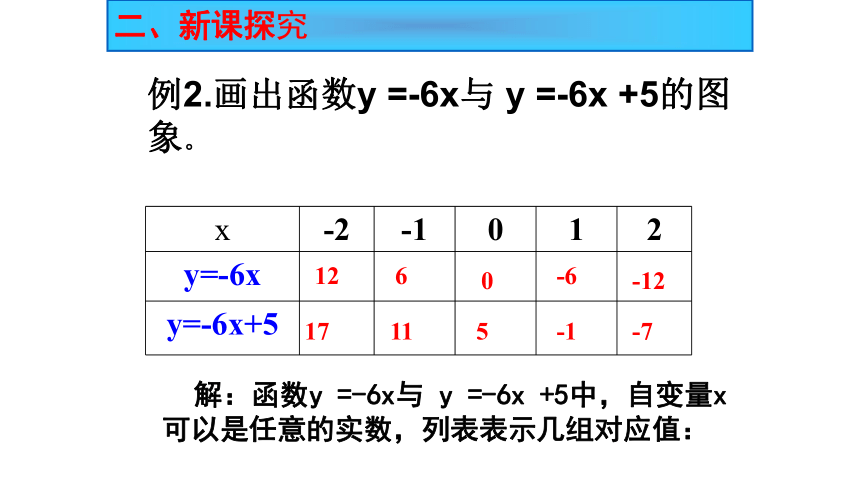
-2
-1
0
1
2
y=-6x
y=-6x+5
6
0
-6
-12
12
17
11
5
-1
-7
例2.画出函数y =-6x与 y =-6x +5的图象。
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:
二、新课探究
17
11
5
-7
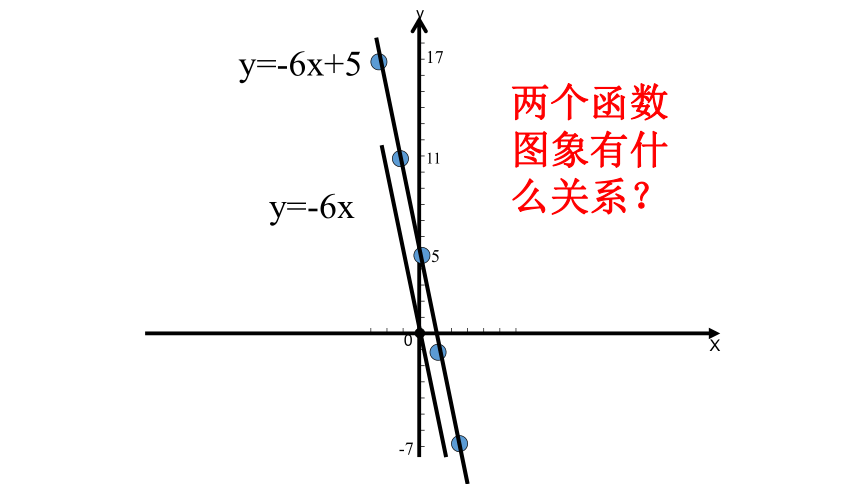
y=-6x
y=-6x+5
两个函数图象有什么关系?
0
X
y
x
y
0
1
5
y=-6x+5
y=-6x
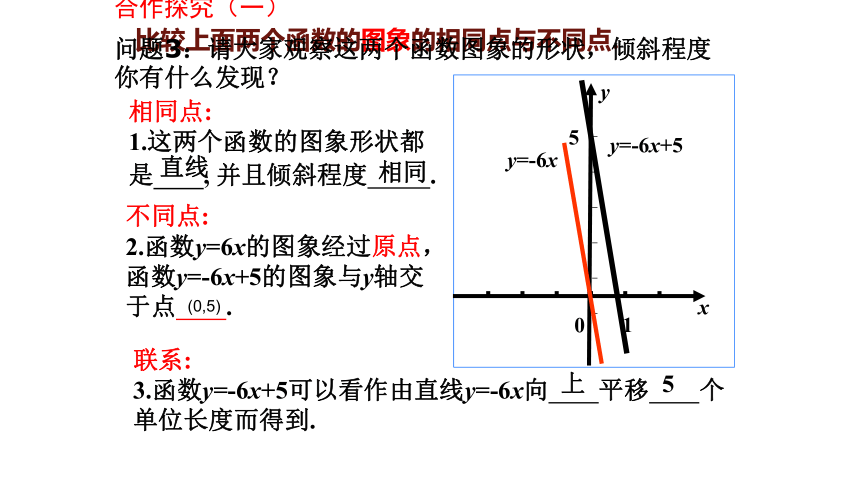
不同点:
2.函数y=6x的图象经过原点,函数y=-6x+5的图象与y轴交于点 .
比较上面两个函数的图象的相同点与不同点.
相同点:
1.这两个函数的图象形状都是 , 并且倾斜程度 .
联系:
3.函数y=-6x+5可以看作由直线y=-6x向 平移 个单位长度而得到.
问题3:请大家观察这两个函数图象的形状,倾斜程度你有什么发现?
合作探究(一)
(0,5)
比较两个函数解析式,你能说出这两个函数图象有平移关系的道理吗?
y=-6x+5
y=-6x
联系:
3.对于自变量x的任一值,这两个函数相应的y值总相差 。
相同点:
1.这两个函数解析式都是自变量x的 (常数)倍,与一个常数的和。
不同点:
2.这两个函数解析式仅在 有区别。
-6
常数项
推广:
(1)所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx _________ 而得到
一条直线;
互相平行
平移 个单位
当b>0,向上平移b个单位;
当b<0,向下平移 个单位。
其中,b叫做直线 y=kx+b在y轴上的截距。
巩固练习
(1)直线y=2x-3可以由直线y=2x经过____________ 而得到;
直线y=-3x+2可以由直线y=-3x经过_______________而得到;
向下平移3个单位
向上平移2个单位
(2)将直线y=-2x-1向上平移3个单位,得到的直线是______.
y=-2x+2
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
2、用两点法画一次函数图像
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
例3:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
一次函数y=kx+b有下列性质:
?1.当k>0时,y随x的增大而_____ 这时函数的图象从左到右_____
?(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
增大
上升
y
x
o
2
1
·
·
·
·
y=2x+1
y=-2x+l
y=x+1
y=-x+1
观察四个函数的图像,分析在一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
画出函数y=x+1,y=-x+1,
y=2x+1,y=-2x+1的图象.
操作探究
解:经过点(0,1),(-1,0)
画出直线y=x+1,经过点(0,1)
,(1,0)画出直线y=-x+1;
经过点(0,1),(-0.5,0)画出直线y=2x+1; 经过点(0,1),(0.5,
0)画出直线y=-2x+1
当k>0时,y随x的增大而______;
当k<0时,y随x的增大而______.
增大
减小
观察前面一次函数的图象,可以发现规律:当k>0时,直线y=kx+b从左向右上升; k<0时直线y=kx+b从左向右下降.由此得出一次函数y=kx+b (k,b是常数,k≠ 0)具有如下性质:
观察归纳
一次函数 y=kx+b
b 决定直线与y轴交点位置
当b>0时,直线交于y正半轴
x
y
0
x
y
0
4.当 b 相等时,直线交于y轴上同一点
2.当b<0时,直线交于y负半轴
3.当b = 0时,直线交于坐标原点
x
y
0
x
x
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
x
y
正撇负捺;上加下减
1.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )
(A)
(B)
(C)
(D)
B
2.下列函数中,y的值随x值的增大而增大的函数是________.
A.y=-2x B.y=-2x+1
C.y=x-2 D.y=-x-2
C
3.对于函数y=5x+6,y的值随x的值减小而______。
减少
2.当k>0时,y随x的增大而______;
当k<0时,y随x的增大而______.
增大
减小
1. 一次函数y=kx+b (k,b是常数,k≠ 0)的图象是一条直线
课堂小结
3.b 决定直线与y轴交点位置
4)当 b 相等时,直线交于y轴上同一点
1)当b>0时,直线交于y正半轴
2)当b<0时,直线交于y负半轴
3)当b = 0时,直线交于坐标原点
作业 必做:书93页练习2,3题
99页4、5题
选做:书 99页 12题
第19章 一次函数
19.2.2 一次函数(第2课时)
1、什么叫正比例函数、一次函数?它们之间有什么关系?
2、正比例函数的图象是什么形状?
一般地,形如 的函数,叫做正比例函数;
一般地,形如 的函数,叫做一次函数。
当b=0时,y=kx+b就变成了 ,所以说正比例函数是一种特殊的一次函数。
正比例函数的图象是( )
y=kx(k是常数,k≠0)
y=kx+b(k,b是常数,k≠0)
y=kx
经过原点的一条直线
一、复习引入
y=kx
图 象
性 质
K>0
y
x
K<0
经过一、三象限
y随x增大而增大
经过二、四象限
y随x增大而减小
正比例函数 y=kx(k是常数,k≠0)中,
k的正负对函数图象有什么影响?
y
x
图像必经过(0,0)和(1,k)这两个点
x
-2
-1
0
1
2
y=-6x
y=-6x+5
6
0
-6
-12
12
17
11
5
-1
-7
例2.画出函数y =-6x与 y =-6x +5的图象。
解:函数y =-6x与 y =-6x +5中,自变量x 可以是任意的实数,列表表示几组对应值:
二、新课探究
17
11
5
-7
y=-6x
y=-6x+5
两个函数图象有什么关系?
0
X
y
x
y
0
1
5
y=-6x+5
y=-6x
不同点:
2.函数y=6x的图象经过原点,函数y=-6x+5的图象与y轴交于点 .
比较上面两个函数的图象的相同点与不同点.
相同点:
1.这两个函数的图象形状都是 , 并且倾斜程度 .
联系:
3.函数y=-6x+5可以看作由直线y=-6x向 平移 个单位长度而得到.
问题3:请大家观察这两个函数图象的形状,倾斜程度你有什么发现?
合作探究(一)
(0,5)
比较两个函数解析式,你能说出这两个函数图象有平移关系的道理吗?
y=-6x+5
y=-6x
联系:
3.对于自变量x的任一值,这两个函数相应的y值总相差 。
相同点:
1.这两个函数解析式都是自变量x的 (常数)倍,与一个常数的和。
不同点:
2.这两个函数解析式仅在 有区别。
-6
常数项
推广:
(1)所有一次函数y=kx+b的图象都是________
(2)直线 y=kx+b与直线y=kx__________;
(3)直线 y=kx+b可以看作由直线y=kx _________ 而得到
一条直线;
互相平行
平移 个单位
当b>0,向上平移b个单位;
当b<0,向下平移 个单位。
其中,b叫做直线 y=kx+b在y轴上的截距。
巩固练习
(1)直线y=2x-3可以由直线y=2x经过____________ 而得到;
直线y=-3x+2可以由直线y=-3x经过_______________而得到;
向下平移3个单位
向上平移2个单位
(2)将直线y=-2x-1向上平移3个单位,得到的直线是______.
y=-2x+2
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
2、用两点法画一次函数图像
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
例3:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
一次函数y=kx+b有下列性质:
?1.当k>0时,y随x的增大而_____ 这时函数的图象从左到右_____
?(2) 当k<0时,y随x的增大而_____,这时函数的图象从左到右_____.
减小
下降
增大
上升
y
x
o
2
1
·
·
·
·
y=2x+1
y=-2x+l
y=x+1
y=-x+1
观察四个函数的图像,分析在一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
画出函数y=x+1,y=-x+1,
y=2x+1,y=-2x+1的图象.
操作探究
解:经过点(0,1),(-1,0)
画出直线y=x+1,经过点(0,1)
,(1,0)画出直线y=-x+1;
经过点(0,1),(-0.5,0)画出直线y=2x+1; 经过点(0,1),(0.5,
0)画出直线y=-2x+1
当k>0时,y随x的增大而______;
当k<0时,y随x的增大而______.
增大
减小
观察前面一次函数的图象,可以发现规律:当k>0时,直线y=kx+b从左向右上升; k<0时直线y=kx+b从左向右下降.由此得出一次函数y=kx+b (k,b是常数,k≠ 0)具有如下性质:
观察归纳
一次函数 y=kx+b
b 决定直线与y轴交点位置
当b>0时,直线交于y正半轴
x
y
0
x
y
0
4.当 b 相等时,直线交于y轴上同一点
2.当b<0时,直线交于y负半轴
3.当b = 0时,直线交于坐标原点
x
y
0
x
x
-5
-4
-3
-2
-1
5
4
3
2
1
-1 0
-2
-3
-4
-5
1
2
3
4
5
x
y
正撇负捺;上加下减
1.下列哪个图像是一次函数y=-3x+5
和y=2x-4的大致图像( )
(A)
(B)
(C)
(D)
B
2.下列函数中,y的值随x值的增大而增大的函数是________.
A.y=-2x B.y=-2x+1
C.y=x-2 D.y=-x-2
C
3.对于函数y=5x+6,y的值随x的值减小而______。
减少
2.当k>0时,y随x的增大而______;
当k<0时,y随x的增大而______.
增大
减小
1. 一次函数y=kx+b (k,b是常数,k≠ 0)的图象是一条直线
课堂小结
3.b 决定直线与y轴交点位置
4)当 b 相等时,直线交于y轴上同一点
1)当b>0时,直线交于y正半轴
2)当b<0时,直线交于y负半轴
3)当b = 0时,直线交于坐标原点
作业 必做:书93页练习2,3题
99页4、5题
选做:书 99页 12题
