人教版八年级数学下册课件:18.2.2菱形的性质(共30张PPT)
文档属性
| 名称 | 人教版八年级数学下册课件:18.2.2菱形的性质(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 998.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:38:28 | ||
图片预览




文档简介
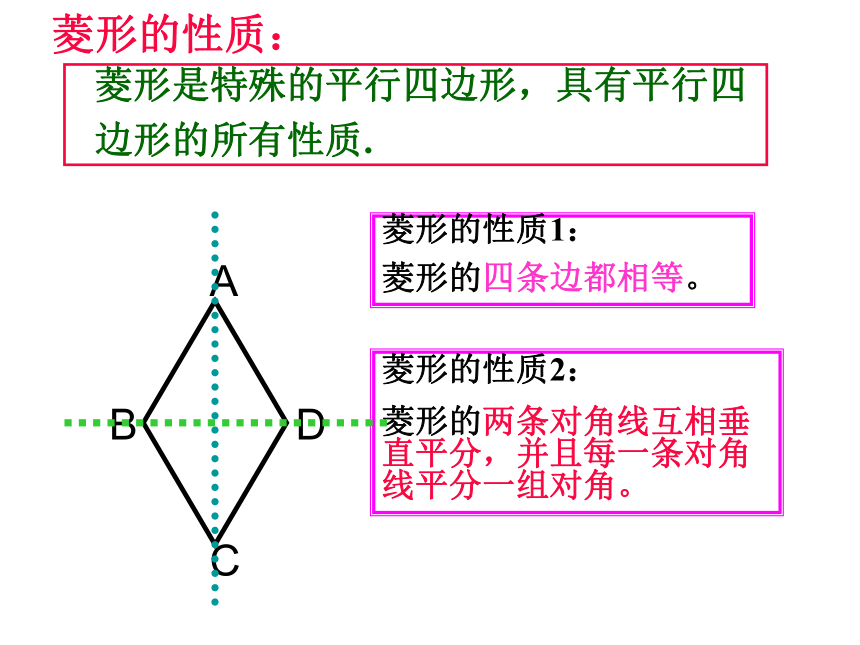
§18.2 .2 菱形的性质
菱形
菱形的性质2:
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角。
菱形是特殊的平行四边形,具有平行四
边形的所有性质.
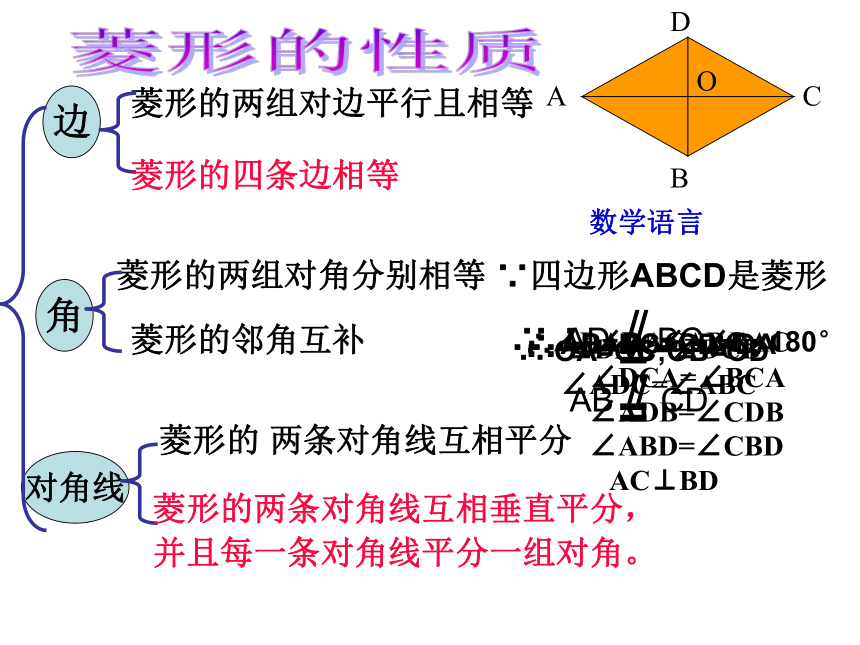
菱形的性质:
B
D
A
C
菱形的性质1:
菱形的四条边都相等。
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角。
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
∴ AB=BC=CD=DA
A
D
C
B
O
∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴ OA=OC;OB=OD
∴ ∠DAB=∠DCB
∠ADC=∠ABC
∴ ∠DAB+∠ABC= 180°
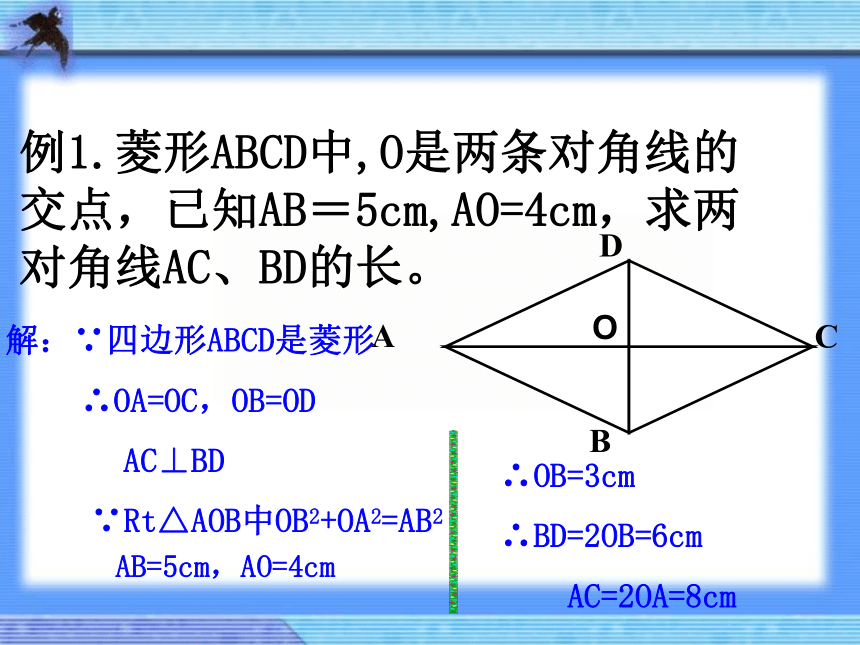
例1.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。
C
B
D
A
O
解:∵四边形ABCD是菱形
∴OA=OC,OB=OD
AC⊥BD
∵Rt△AOB中OB2+OA2=AB2
AB=5cm,AO=4cm
∴OB=3cm
∴BD=2OB=6cm
AC=2OA=8cm
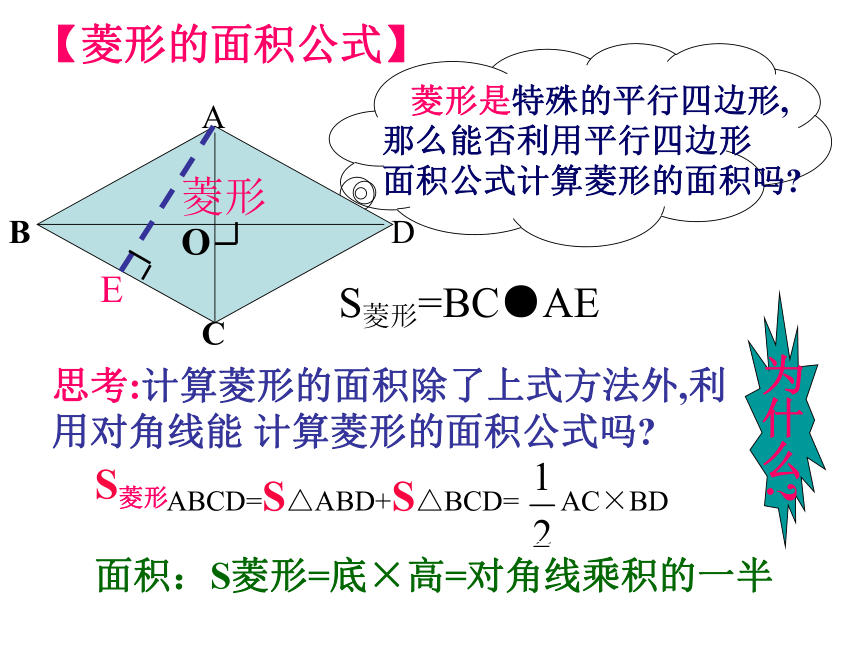
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗?
菱形
A
B
C
D
O
E
S菱形=BC●AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗?
ABCD=S△ABD+S△BCD= AC×BD
S菱形
面积:S菱形=底×高=对角线乘积的一半
为什么?
A
B
C
D
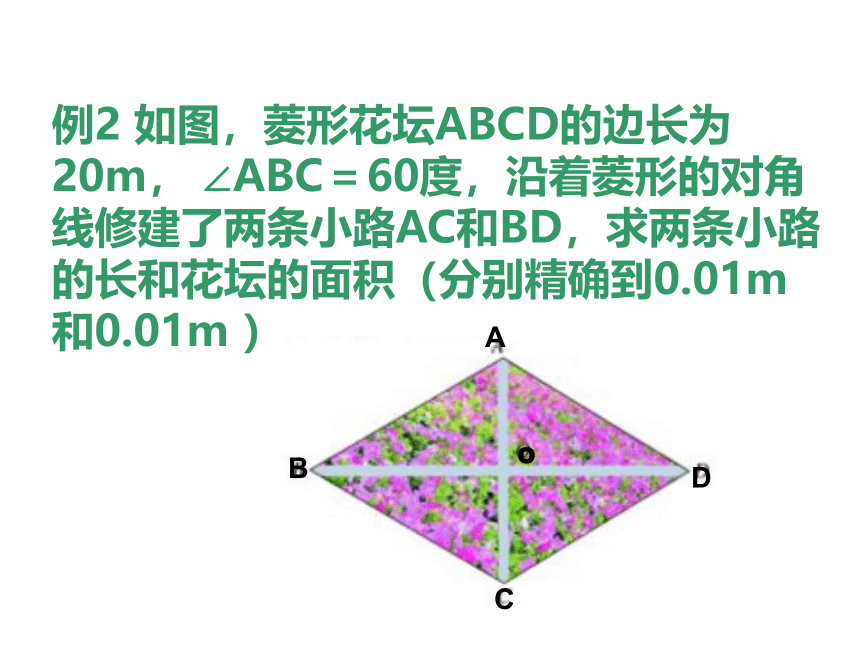
例2 如图,菱形花坛ABCD的边长为20m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m )
O
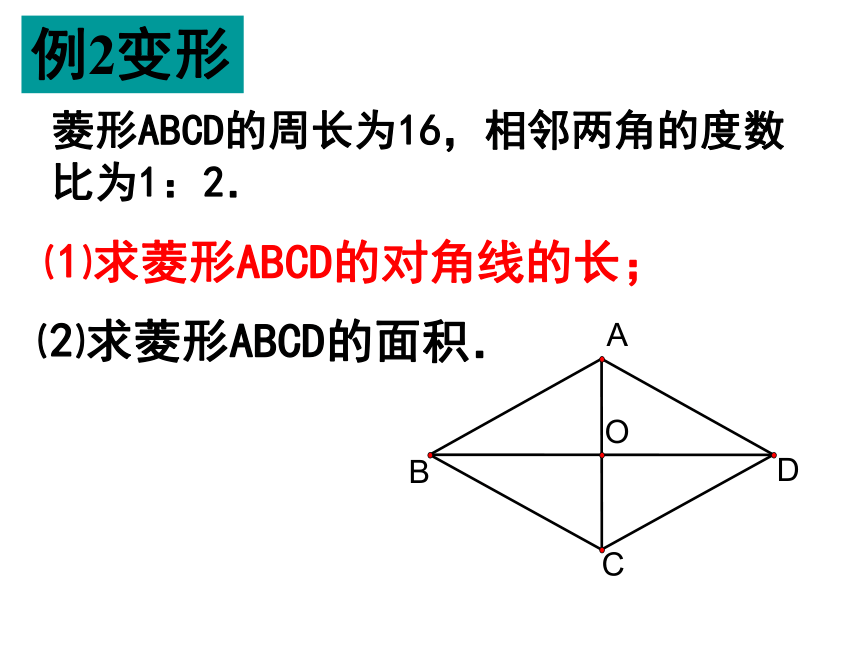
例2变形
D
O
A
C
B
菱形ABCD的周长为16,相邻两角的度数比为1:2.
⑴求菱形ABCD的对角线的长;
⑵求菱形ABCD的面积.
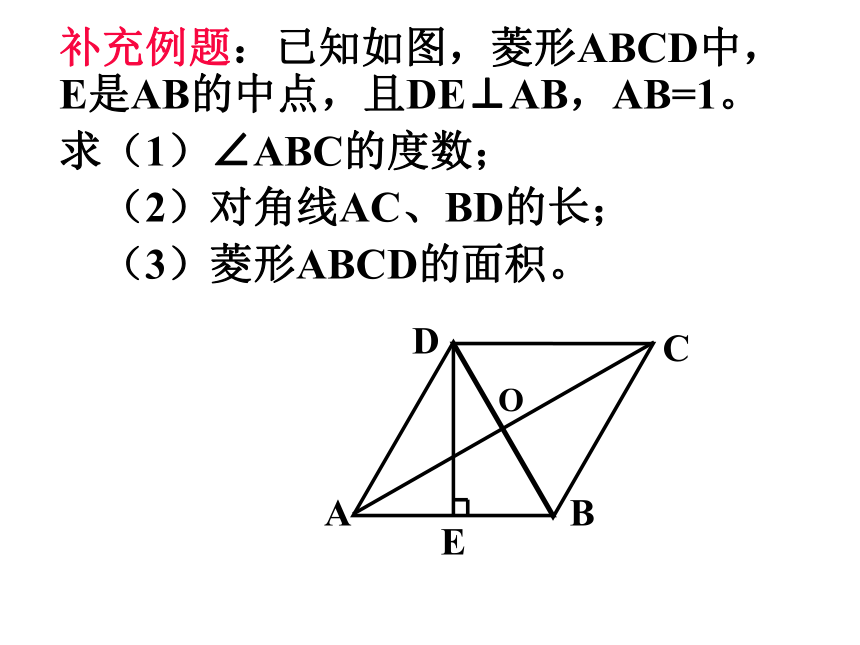
补充例题:已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
1.菱形的定义: 是菱形
2.菱形的性质:①菱形的四条边 ,
②菱形的对角线 ,并且每一条对角线一组 对角.
3.下列说法不正确的有 (填番号)
①菱形的对边平行且相等.②菱形的对角线互相平分
③菱形的对角线相等.④菱形的对角线互相垂直.
⑤菱形的一条对角线平分一组对角.⑥菱形的对角相等.
4.菱形的面积公式:① ② .
5.菱形既是 图形,又是 图形.
活动五:
C
B
D
A
O
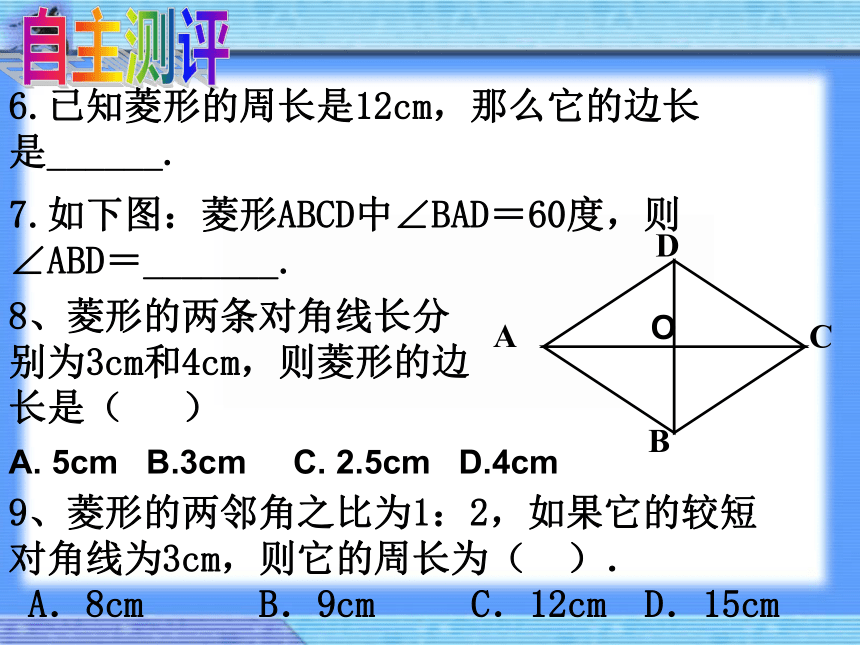
6.已知菱形的周长是12cm,那么它的边长是______.
7.如下图:菱形ABCD中∠BAD=60度,则∠ABD=_______.
8、菱形的两条对角线长分别为3cm和4cm,则菱形的边长是( )
A. 5cm B.3cm C. 2.5cm D.4cm
9、菱形的两邻角之比为1:2,如果它的较短对角线为3cm,则它的周长为( ).
A.8cm B.9cm C.12cm D.15cm
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60度,则∠BAC=_______.
3cm
60度
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
C
A.10cm B.7cm C. 5cm D.4cm
A
B
C
D
O
3
4
4.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )
A.75°B.60°C.45°D.30°
B
5、四边形ABCD是菱形,O是两条对角线的
交点,已知AB=5cm,AO=4cm,求对角
线BD的长。
A
B
C
D
O
解:∵四边形ABCD是菱形
∴AC⊥BD
∴
∴OB=3
∴ BD=2OB=6 cm
5
4
3
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?
课堂反思
四边形
平行四边形
菱形
矩形
四、课堂小结:矩形和菱形的性质
矩形
菱形
定义
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
性
质
1、具有平行四边形的一切性质
2、四个角都是直角
3、矩形的对角线相等
1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
A
B
C
D
E
F
例1、已知:AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形。
A
B
C
D
E
F
1
2
3
变式训练:把本例中的“DE//AC交AB于E, DF ∥AB交AC于F”改成“EF垂直平分AD”,其他条件不变,你能否证明四边形AEDF是菱形?
菱形性质的应用
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度; (2).菱形的面积
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
三、课堂练习(复习巩固)
1、菱形的两条对角线长分别是6cm和8cm,则菱形 的周长 ,面积 。
2、菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为 ;边长为 。
3、已知菱形的两个邻角的比是1:5,高是 8cm,则菱形的周长为 。
4、已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是 。
由此可进一步推导得出:对角线互相垂直的四边形的面积都等于两条对角线乘积的一半。
例1:如图,菱形ABCD的边长为4cm,∠BAD=2 ∠ABC。对角线AC、BD相交于点O,求这个菱形的对角线长和面积。
变式题(1):菱形两条对角线长为6和8,菱形
的边长为 ,面积为 。
(2):菱形ABCD的面积为96,对角线
AC长为16 ,此菱形的边长为 。
(3):菱形对角线的平方和等于一边平方
的 ( )
A. 2倍 B. 3倍 C.4倍 D. 5倍
5
4
10
C
例2:菱形ABCD中,对角线AC、BD相交于点O,E、F分别是AB、AD的中点,求证:OE=OF。
A
B
C
D
E
F
变式题(1):菱形ABCD ,E、F分别ABCD的中点,求证:CE=CF.
(2)如果上题中还有CE⊥AB,
CF⊥AD,求各内角的度数
例3:如果菱形的一个角是1200,那么这个角的顶点向两条对边所引的两条垂线分别平分两边。
A
B
C
D
E
F
已知如图,菱形ABCD中,E、F分别是BC、CD
上的点,且∠B= ∠ EAF=60 , ∠ BAE=18,
求∠ CEF的度数.
思考:已知:菱形中ABCD,∠A=72°,请设计三种不同的分法,将菱形ABCD分成四个三角形,使得每一个三角形都是等腰三角形。
成功就是99%的血汗,加上1%的灵感。
——爱迪生
菱形
菱形的性质2:
菱形的两条对角线互相垂直平分,并且每一条对角线平分一组对角。
菱形是特殊的平行四边形,具有平行四
边形的所有性质.
菱形的性质:
B
D
A
C
菱形的性质1:
菱形的四条边都相等。
菱形的 两条对角线互相平分
菱形的两组对边平行且相等
边
对角线
角
数学语言
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角。
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
∴ AB=BC=CD=DA
A
D
C
B
O
∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD
∴ OA=OC;OB=OD
∴ ∠DAB=∠DCB
∠ADC=∠ABC
∴ ∠DAB+∠ABC= 180°
例1.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。
C
B
D
A
O
解:∵四边形ABCD是菱形
∴OA=OC,OB=OD
AC⊥BD
∵Rt△AOB中OB2+OA2=AB2
AB=5cm,AO=4cm
∴OB=3cm
∴BD=2OB=6cm
AC=2OA=8cm
【菱形的面积公式】
菱形是特殊的平行四边形,
那么能否利用平行四边形
面积公式计算菱形的面积吗?
菱形
A
B
C
D
O
E
S菱形=BC●AE
思考:计算菱形的面积除了上式方法外,利用对角线能 计算菱形的面积公式吗?
ABCD=S△ABD+S△BCD= AC×BD
S菱形
面积:S菱形=底×高=对角线乘积的一半
为什么?
A
B
C
D
例2 如图,菱形花坛ABCD的边长为20m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m )
O
例2变形
D
O
A
C
B
菱形ABCD的周长为16,相邻两角的度数比为1:2.
⑴求菱形ABCD的对角线的长;
⑵求菱形ABCD的面积.
补充例题:已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1。
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。
A
B
C
D
E
O
1.菱形的定义: 是菱形
2.菱形的性质:①菱形的四条边 ,
②菱形的对角线 ,并且每一条对角线一组 对角.
3.下列说法不正确的有 (填番号)
①菱形的对边平行且相等.②菱形的对角线互相平分
③菱形的对角线相等.④菱形的对角线互相垂直.
⑤菱形的一条对角线平分一组对角.⑥菱形的对角相等.
4.菱形的面积公式:① ② .
5.菱形既是 图形,又是 图形.
活动五:
C
B
D
A
O
6.已知菱形的周长是12cm,那么它的边长是______.
7.如下图:菱形ABCD中∠BAD=60度,则∠ABD=_______.
8、菱形的两条对角线长分别为3cm和4cm,则菱形的边长是( )
A. 5cm B.3cm C. 2.5cm D.4cm
9、菱形的两邻角之比为1:2,如果它的较短对角线为3cm,则它的周长为( ).
A.8cm B.9cm C.12cm D.15cm
1.已知菱形的周长是12cm,那么它的边长是______.
2.菱形ABCD中∠ABC=60度,则∠BAC=_______.
3cm
60度
3、菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
C
A.10cm B.7cm C. 5cm D.4cm
A
B
C
D
O
3
4
4.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )
A.75°B.60°C.45°D.30°
B
5、四边形ABCD是菱形,O是两条对角线的
交点,已知AB=5cm,AO=4cm,求对角
线BD的长。
A
B
C
D
O
解:∵四边形ABCD是菱形
∴AC⊥BD
∴
∴OB=3
∴ BD=2OB=6 cm
5
4
3
有关菱形问题可转化为直角三角形或等腰三角形的问题来解决
1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?
课堂反思
四边形
平行四边形
菱形
矩形
四、课堂小结:矩形和菱形的性质
矩形
菱形
定义
有一个角是直角的平行四边形
有一组邻边相等的平行四边形
性
质
1、具有平行四边形的一切性质
2、四个角都是直角
3、矩形的对角线相等
1、具有平行四边形的一切性质
2、菱形的四条边都相等
3、菱形的对角线互相垂直,并且每一条对角线平分一组对角
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
A
B
C
D
E
F
例1、已知:AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F,求证:四边形AEDF是菱形。
A
B
C
D
E
F
1
2
3
变式训练:把本例中的“DE//AC交AB于E, DF ∥AB交AC于F”改成“EF垂直平分AD”,其他条件不变,你能否证明四边形AEDF是菱形?
菱形性质的应用
已知:如图,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm.
求:(1).对角线AC的长度; (2).菱形的面积
解:(1)
∵四边形ABCD是菱形,
=2×△ABD的面积
∴∠AED=900,
(2)菱形ABCD的面积=△ABD的面积+△CBD的面积
∴AC=2AE=2×12=24(cm).
D
B
C
A
E
三、课堂练习(复习巩固)
1、菱形的两条对角线长分别是6cm和8cm,则菱形 的周长 ,面积 。
2、菱形的面积为24cm2,一条对角线的长为6cm,则另一条对角线长为 ;边长为 。
3、已知菱形的两个邻角的比是1:5,高是 8cm,则菱形的周长为 。
4、已知菱形的周长为40cm,两对角线的比为3:4,则两对角线的长分别是 。
由此可进一步推导得出:对角线互相垂直的四边形的面积都等于两条对角线乘积的一半。
例1:如图,菱形ABCD的边长为4cm,∠BAD=2 ∠ABC。对角线AC、BD相交于点O,求这个菱形的对角线长和面积。
变式题(1):菱形两条对角线长为6和8,菱形
的边长为 ,面积为 。
(2):菱形ABCD的面积为96,对角线
AC长为16 ,此菱形的边长为 。
(3):菱形对角线的平方和等于一边平方
的 ( )
A. 2倍 B. 3倍 C.4倍 D. 5倍
5
4
10
C
例2:菱形ABCD中,对角线AC、BD相交于点O,E、F分别是AB、AD的中点,求证:OE=OF。
A
B
C
D
E
F
变式题(1):菱形ABCD ,E、F分别ABCD的中点,求证:CE=CF.
(2)如果上题中还有CE⊥AB,
CF⊥AD,求各内角的度数
例3:如果菱形的一个角是1200,那么这个角的顶点向两条对边所引的两条垂线分别平分两边。
A
B
C
D
E
F
已知如图,菱形ABCD中,E、F分别是BC、CD
上的点,且∠B= ∠ EAF=60 , ∠ BAE=18,
求∠ CEF的度数.
思考:已知:菱形中ABCD,∠A=72°,请设计三种不同的分法,将菱形ABCD分成四个三角形,使得每一个三角形都是等腰三角形。
成功就是99%的血汗,加上1%的灵感。
——爱迪生
