人教版八年级下册 第十九章一次函数(单元培优)(共59张PPT)
文档属性
| 名称 | 人教版八年级下册 第十九章一次函数(单元培优)(共59张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-03-03 18:53:25 | ||
图片预览






文档简介
第19章 一次函数综合练习
01
一次函数与选填运用
02
一次函数与面积问题
03
一次函数与实际问题
目录
04
一次函数与几何图形存在性问题
05
一次函数与动点问题
Part1 一次函数与选填运用
一次函数与选填运用
Part 1
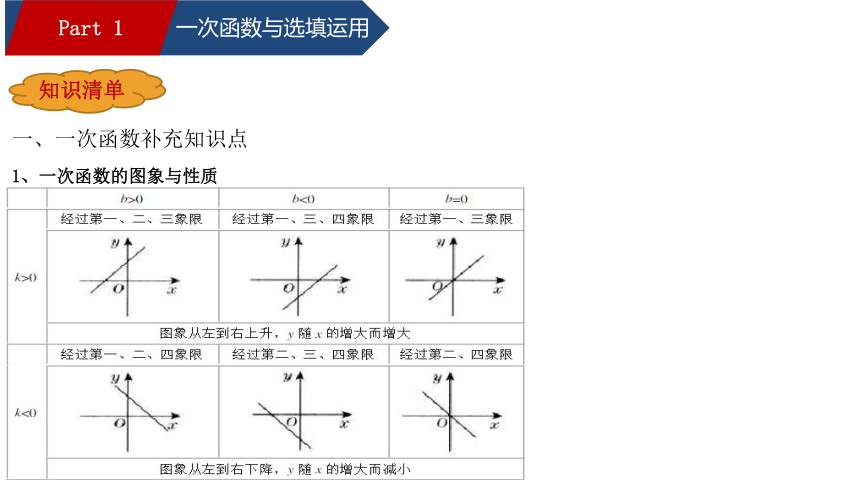
一、一次函数补充知识点
1、一次函数的图象与性质
知识清单
一次函数与选填运用
Part 1
2、一次函数的特殊点
一次函数与x轴交点为(-bk,0),与y轴交点为(0,b),所以一次函数与y轴交点的纵坐标就是b的值.
3、k值
1)大小判断,当k>0时,一次函数图象与x轴夹角越大,k值越大;当k<0时,一次函数图象与x轴夹角越大,k值越小.
2)计算:设一次函数图象上有两点A(x1, y1?)、B( x2, y2?),则k=y1?y2x1?x2(要么分子分母前面都是y1?、x1?;要么分子分母前面都是y2?、x2?)
3)k值与特殊角:当k=±33时,一次函数与x轴夹角30°;当k=±1时,一次函数与x轴夹角45°;当k=±3时,一次函数与x轴夹角60°.
4)设两一次函数图象平行,则k1= k2?;两一次函数图象垂直,则k1 ?k2?=-1
?
一次函数与选填运用
Part 1
4、中点坐标公式:设坐标系中有两点A(x1, y1?)、B( x2, y2?),C为线段AB的中点,则C点坐标为(x1+x22,y1+y22?).
5、两点间距离公式:设坐标系中有两点A(x1, y1?)、B( x2, y2?),则:
AB=(x1?x2)2+(y1?y2)2
6、一元二次方程配方法求解
如:x2-4x+3=0→ x2-4x=-3 → x2-4x+4=-3+4 → (x?2)2=1 →x-2=±1 →x1=1+2=3x2=?1+2=1
?
知识清单
一次函数与选填运用
Part 1
1.1 一次函数与特殊点问题
例1、如图所示,直线y=k(x-2)+k+1与x轴、y轴分别交于B、C两点,且????????????????=12?.则k的值为( )
A. 13 B. 12
C.1 D.2
变式训练:在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )
A.5 B.4 C.3 D.2
?
一次函数与选填运用
Part 1
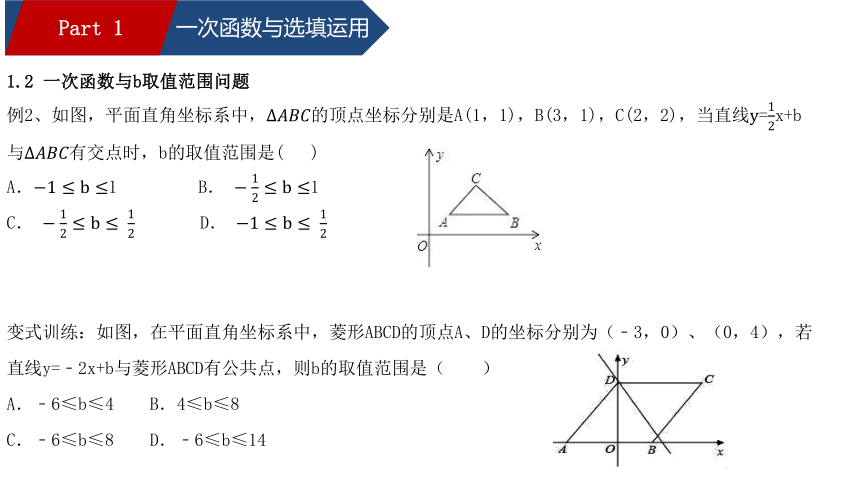
1.2 一次函数与b取值范围问题
例2、如图,平面直角坐标系中,?????????????的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线y=12x+b与?????????????有交点时,b的取值范围是( )
A.?1≤b≤1 B. ?12≤b≤1
C. ?12≤b≤ 12 D. ?1≤b≤ 12
变式训练:如图,在平面直角坐标系中,菱形ABCD的顶点A、D的坐标分别为(﹣3,0)、(0,4),若直线y=﹣2x+b与菱形ABCD有公共点,则b的取值范围是( )
A.﹣6≤b≤4 B.4≤b≤8
C.﹣6≤b≤8 D.﹣6≤b≤14
?
一次函数与选填运用
Part 1
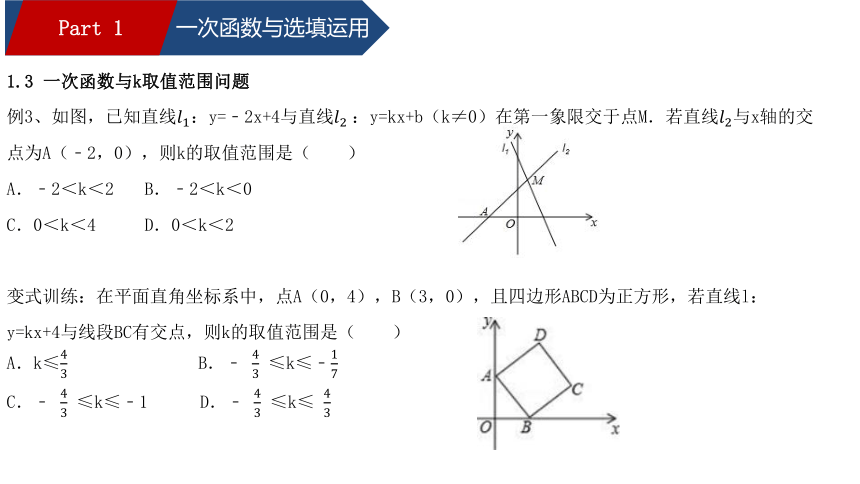
1.3 一次函数与k取值范围问题
例3、如图,已知直线????1:y=﹣2x+4与直线????2?:y=kx+b(k≠0)在第一象限交于点M.若直线????2与x轴的交点为A(﹣2,0),则k的取值范围是( )
A.﹣2<k<2 B.﹣2<k<0
C.0<k<4 D.0<k<2
变式训练:在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )
A.k≤43 B.﹣ 43 ≤k≤﹣17?
C.﹣ 43 ≤k≤﹣1 D.﹣ 43 ≤k≤ 43
?
一次函数与选填运用
Part 1
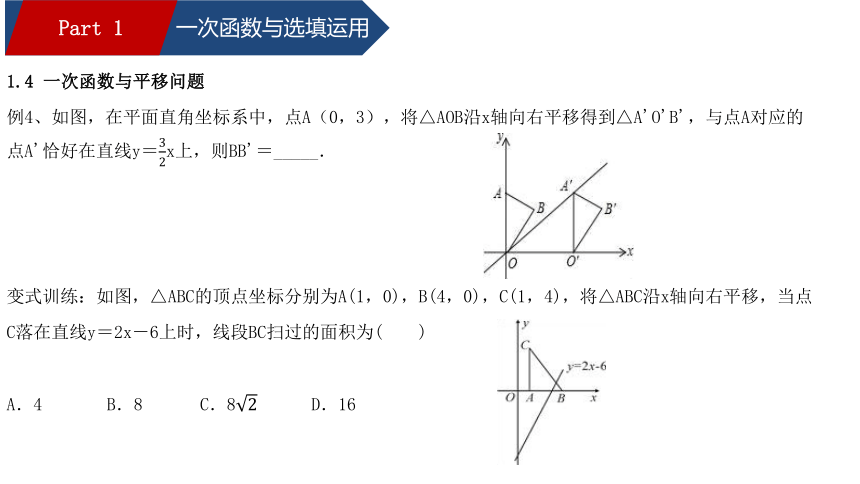
1.4 一次函数与平移问题
例4、如图,在平面直角坐标系中,点A(0,3),将△AOB沿x轴向右平移得到△A'O'B',与点A对应的点A'恰好在直线y=32x上,则BB'=_____.
变式训练:如图,△ABC的顶点坐标分别为A(1,0),B(4,0),C(1,4),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
A.4 B.8 C.82 D.16
?
一次函数与选填运用
Part 1
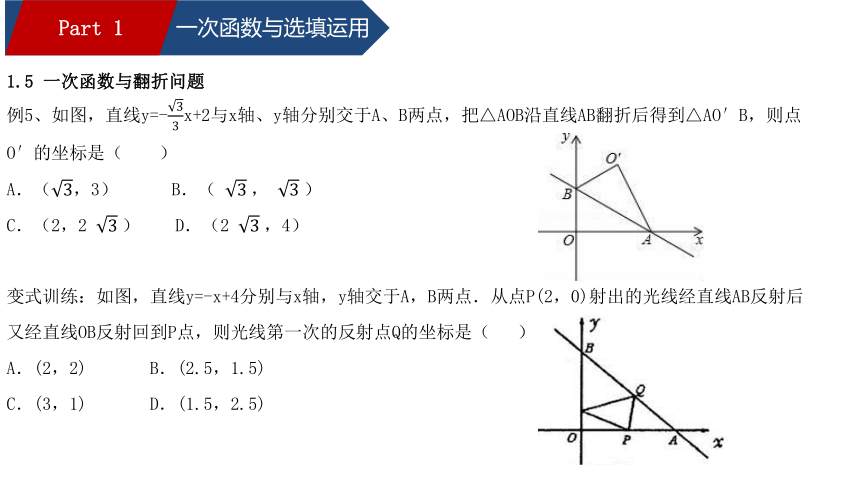
1.5 一次函数与翻折问题
例5、如图,直线y=-33x+2与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( )
A.(3,3) B.( 3?, 3?)
C.(2,2 3?) D.(2 3?,4)
变式训练:如图,直线y=-x+4分别与x轴,y轴交于A,B两点.从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )
A.(2,2) B.(2.5,1.5)
C.(3,1) D.(1.5,2.5)
?
一次函数与选填运用
Part 1
1.6 一次函数与不等式问题
例6、如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b<0的解集为( )
A.x<1 B.x>1
C. x<3 D. x>3
变式训练:如图所示,函数y1=x?和y2=13x+ 43的图象相交于(–1,1),(2,2)两点.当y1 > y2时,x的取值范围是( )
A.x<–1 B.x<–1或x>2
C.x>2 D.–1?
一次函数与选填运用
Part 1
1.7 一次函数与面积问题
例7、如图,点A,B,C在一次函数y=-2x+m的图象上,它们的横坐标依次为 ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A.1 B.3 C.3(m-1) D.32(m-2)
变式训练:如图,在平面直角坐标系xoy中,直线l的解析式为y=-33+1,该直线与x轴、y轴分别交于点A、B,以AB为边在第一象限内作正△ABC.若点P(m,n)在第一象限内,且满足?????????????????=??????????????????,则n的取值范围是( )
A.0C.n>3 D.2?
一次函数与选填运用
Part 1
1.8 一次函数与最短路径问题
例8、如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B.(-12?,- 12?)
C.(22?, -22?) D.( -22?, -22?)
变式训练:直线y=23?x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(-3,0) B.(-6,0)
C.(-52?,0) D.(- 32?,0)
?
一次函数与选填运用
Part 1
1.9 一次函数与图象分析问题
例9、在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
A.乙先出发的时间为0.5小时
B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇
D.甲到B地比乙到A地早112?小时
?
一次函数与选填运用
Part 1
1.9 一次函数与图象分析问题
变式训练:如图,已知线段AB=12厘米,动点P以2厘米/秒的速度从点A出发向点B运动,动点Q以4厘米/秒的速度从点B出发向点A运动.两点同时出发,到达各自的终点后停止运动.设两点之间的距离为s(厘米),动点P的运动时间为t秒,则下图中能正确反映s与t之间的函数关系的是( )
A、 B、 C、 D、
一次函数与选填运用
Part 1
1.10 一次函数与规律探究问题
例10、如图,在平面直角坐标系中,直线l:y=33x+1交x轴于点A,交y轴于点B,点????1?、 ????2?、 ????3?,…在x轴的正半轴上,点????1?、 ????2?、 ????3?,…在直线l上.若△O ????1?????1?,△ ????1?????2?????2?,△ ????2?????3?????3?,…均为等边三角形,则△ ????6?????7?????7?的周长是______.
变式训练:如图,在平面直角坐标系中,点????1?、 ????2?、 ????3?…都在x轴上,点????1?、 ????2?、 ????3?…都在直线y=x上,O ????1?=1,且△ ????1?????1?????2?,△ ????2?????2?????3?,△ ????3 ????3?????4?,… ????n ????n?????n+1?…分别是以????1?、 ????2?、 ????3?,… ????n?…为直角顶点的等腰直角三角形,则△ ????10 ????10?????11?的面积是________.
?
一次函数与选填运用
Part 1
1.11 一次函数与其他
例11、已知k=a+b?cc?=a?b+cb =?a+b+ca,且m?5?+n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.
A.一、二 B.二、三 C.三、四 D.一、四
变式训练:如图,在直角坐标系中,等腰直角△ABO的O点是坐标原点,A的坐标是(﹣4,0),直角顶点B在第二象限,等腰直角△BCD的C点在y轴上移动,我们发现直角顶点D点随之在一条直线上移动,这条直线的解析式是( )
A.y=﹣2x+1 B.y=﹣12?x+2
C.y=﹣3x﹣2 D.y=﹣x+2
?
Part2 一次函数与面积问题
一次函数与面积问题
Part 2
1、面积问题常见分类
模型一:所有点均可求
A、B、C、D、E的坐标均可求,求?????????????????.
方法1:拆三角形
?????????????????= ?????????????????+ ?????????????????=12?BE?y????+ 12?BE?y????
方法2:补三角形
?????????????????= ?????????????????- ?????????????????= 12?AD?????????- 12?AD?????????
?
知识清单
一次函数与面积问题
Part 2
模型二:面积存在性问题
条件:A、O、B、C为定点(坐标可求),若点D在y轴
上,且满足?????????????????=13??????????????????,求D点坐标.
思路分析:此类问题一定有一个图形面积已知,通过该
图形的面积得出另一个图形的面积,另一个图形一定有
两个定点,一个动点,而且要么高是定值,要么底是定值.
详解: ?????????????????的值可求,所以可以通过等量关系求出?????????????????,因为?????????????的高为xc定值,所以OD长可求,设D点坐标为(0,m),则m?yo=OD,求解即可.
?
知识清单
一次函数与面积问题
Part 2
模型三:等面积找点
解题依据:利用两平行线之间的距离处处相等找点.
题目类型:A、B、C坐标已知,????为动点,?????????????????=?????????????????,且D点
过(m,52),则m的值为?
解题方法:求出直线AB的解析式,确定k值,因为C点坐标已
知,所以过C点的平行线也就可求解析式了,最后只需将D点
带入求出的过C点的平行线解析式就可求解出m的值.
?
知识清单
一次函数与面积问题
Part 2
2.1 模型一:拆补法求面积
例12:如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积.
一次函数与面积问题
Part 2
2.1 模型一:拆补法求面积
变式训练:如图,直线y=32?x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y= 32?x+m相交于点D,
(1)求D点的坐标;
(2)求四边形AOCD的面积;
?
一次函数与面积问题
Part 2
2.2 模型二:面积存在性问题
例13:如图,一次函数y=kx+b的图象经过点A(-2,6),且与x轴相交于点B,与正比例函数 y=3x的图象相交于点C,点C的横坐标为1.
(1)求一次函数y=kx+b的表达式;
(2)若点D在y轴负半轴上,且满足?????????????????=12??????????????????,求点D的坐标.
?
一次函数与面积问题
Part 2
2.2 模型二:面积存在性问题
变式训练:如图,在平面直角坐标系中,直线y=-x+6与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
①求点B和点C的坐标.
②求△OAC的面积.
③是否存在点M,使△OMC的面积是△OAC的面积的14??若存在,求出此时点M的坐标,若不存在,说明理由.
?
一次函数与面积问题
Part 2
2.3 模型三:等面积找点
例14:如图,在平面直角坐标系中,A(0,8),B(4,0),AB的垂直平分线交y轴与点D,连接BD,M(a,1)为第一象限内的点
(1)则D(____, ____),并求直线BD的解析式;
(2)当?????????????????=??????????????????时,求a的值;
?
一次函数与面积问题
Part 2
2.3 模型三:等面积找点
变式训练:如图,点A(1,0),B(0,3?)分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求直线AB的解析式及点C的坐标;
(2)若点P(m,32?)为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
?
Part3 一次函数与实际问题
一次函数与实际问题
学习任务三
3.1 分段函数
例15:赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)求甲、乙两支龙舟队之间的距离m与x的函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
一次函数与实际问题
学习任务三
3.1 分段函数
变式训练:都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2:1.
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式.
(3)在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.
一次函数与实际问题
学习任务三
3.2 不等式与函数增减性运用
例16:2017年遂宁市吹响了全国文明城市创建决胜“集结号”.为了加快创建步伐,某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方.已知一辆大型渣土运输车和一辆小型渣土运输车每次共运15吨;3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该渣土运输公司决定派出大小两种型号渣土运输车共20辆参与运输土方,若每次运输土方总量不小于148吨,且小型渣土运输车至少派出7辆,问该渣土运输公司有几种派出方案?
(3)在(2)的条件下,已知一辆大型渣土运输车运输话费500元/次,一辆小型渣土运输车运输花费300元/次,为了节约开支,该公司应选择哪种方案划算?
一次函数与实际问题
学习任务三
3.2 不等式与函数增减性运用
变式训练:为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
一次函数与实际问题
学习任务三
3.3 一次函数与最优方案问题
例17:某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件.已知生产1件A种产品,需要甲种原料9kg,乙种原料3kg,可获利润700元;生产1件B种产品,需要甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A,B两种产品的生产件数,有哪几种方案?请设计出来.
(2)设生产A,B两种产品所获总利润为y(元),其中一种产品的生产件数为x,试写出y关于x的函数解析式,并利用函数的性质说明(1)中哪种生产方案所获总利润最大,最大利润是多少.
一次函数与实际问题
学习任务三
3.3 一次函数与最优方案问题
变式训练:学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
一次函数与实际问题
学习任务三
3.4 一次函数与图象分析问题
例18:一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
(1)甲、乙两地之间的距离为______ km ;图中点 C 的实际意义为:______;慢车的速度为______,快车的速度为______;
(2)求线段 BC 所表示的 y 与 x 之间的函数关系式;(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.求第二列快车出发多长时间,与慢车相距200km.
一次函数与实际问题
学习任务三
3.4 一次函数与图象分析问题
变式训练:甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是_____,B点表示的实际意义是_____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
一次函数与实际问题
学习任务三
3.5 一次函数与参数问题
例19:某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
一次函数与实际问题
学习任务三
3.5 一次函数与参数问题
变式训练:为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元,售价320元;乙种服装每件进价150元,售价280元.
(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?
(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0Part4一次函数与几何图形存在性问题
一次函数与几何图形存在性问题
学习任务四
4.1 一次函数与全等三角形存在性问题
例20:如图,一次函数y=34x+6的图象与x,y轴分别交于A,B两点,点C与点A关于y轴对称.动点P,Q分别在线段AC,AB上(点P与点A,C不重合),且满足∠BPQ=∠BAO.
(1)求点A,B的坐标及线段BC的长度;
(2)当点P在什么位置时,?APQ≌?CBP,说明理由;
?
一次函数与几何图形存在性问题
学习任务四
4.1 一次函数与全等三角形存在性问题
变式训练:如图,直线y=-43x+4与x轴和y轴分别交于A、B两点,另一条直线过点A和点C(7,3).
(1)求直线AC的函数表达式;
(2)求证:AB⊥AC;
(3)若点P是直线AC上的一个动点,点Q是X轴上的一个动点,且以PQA为顶点的三角形与?????????????全等,求点Q的坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.2 一次函数与等腰三角形存在性问题
例21:如图,直线????1: y1?=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线????1上一点,另一直线????2?: y2?=12x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线????2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②求出t为多少时,△APQ的面积小于3;
③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
?
一次函数与几何图形存在性问题
学习任务四
4.2 一次函数与等腰三角形存在性问题
变式训练:一次函数y=﹣33?x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC.
(1)求△ABC的面积和点C的坐标;
(2)如果在第二象限内有一点P(a,12?),试用含a的代数式表示四边形ABPO的面积.
(3)在x轴上是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
?
一次函数与几何图形存在性问题
学习任务四
4.3 一次函数与直角三角形存在性问题
例22:如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
一次函数与几何图形存在性问题
学习任务四
4.3 一次函数与直角三角形存在性问题
变式训练:如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角角形?如果存在,求出点M的坐标;如果不存在,说明理由.
一次函数与几何图形存在性问题
学习任务四
4.4 一次函数与等腰直角三角形存在性问题
例23:(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线????1?:y=43x+4与坐标轴交于点A、B,将直线????1绕点A逆时针旋转45°至直线????2?,如图2,求直线????2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.4 一次函数与等腰直角三角形存在性问题
变式训练:如图,在平面直角坐标系中,直线????1的解析式为y=-x,直线????2与????1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+b+3=0.
(1)求直线????2的解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与????1?, ????2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.5 一次函数与平行四边形存在性问题
例24:如图,已知函数y=-13?x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=- 13?x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
?
一次函数与几何图形存在性问题
学习任务四
4.5 一次函数与平行四边形存在性问题
变式训练:如图,在平面直角坐标系中,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,线段OA,OC的长分别是m,n且满足(?????6)2+?????8=0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处.
(1)求线段OD的长
(2)求点E的坐标
(3)DE所在直线与AB相交于点M,点N在x轴的正半轴上,以M、A、N、C为顶点的四边形是平行四边形时,求N点坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.6 一次函数与菱形存在性问题
例25:如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,AB=5,OA:OB =3:4.
(1)求直线l的表达式;
(2)点P是y轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
一次函数与几何图形存在性问题
学习任务四
4.6 一次函数与菱形存在性问题
变式训练:如图,在平面直角坐标系中,直线????1?:y=-12x+6分别与x轴、y轴交于点B、C,且与直线????2?: y= 12x交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.
?
一次函数与几何图形存在性问题
学习任务四
4.7 一次函数与正方形存在性问题
例26:如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2,1).
(1)求k,b的值;
(2)P为直线AB上一点,PC⊥x轴于点C,PD⊥y轴于点D,若四边形PCOD为正方形,求点P的坐标.
一次函数与几何图形存在性问题
学习任务四
4.7 一次函数与正方形存在性问题
变式训练:如图,已知一次函数y=﹣12?x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=13?MP,MB= 13?OM,OE= 13?ON,ND= 13?NP.
(1)求b的值;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣ 12?x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
?
Part5 一次函数与动点问题
一次函数与动点问题
学习任务五
5.1 一次函数与动点问题
例27:已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
一次函数与动点问题
学习任务五
5.1 一次函数与动点问题
变式训练:在矩形ABCD中AB=16,AD=12,点M是AD的中点,点N是CD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,速度为2单位长度/秒,点Q从N点出发沿N→C→B→A的路线匀速运动,速度为1单位长度/秒,P、Q两点同时运动,时间为t秒,若其中一点到达终点,另一点也随即停止运动.
(1)如图1,若矩形ABCD与∠PMA重叠部分的面积为y.
①求当t=4,10,16时,y的值.
②求y关于t的函数解析式.
(2)当以M、D、P、Q四个点为顶点的四边形是平行四边形时,求出此时t的值.
一次函数与动点问题
学习任务五
5.2 一次函数与动直线、动图形问题
例28:如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D.
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0①当平移距离a=1时, 正方形OCMD与△AOB重叠部分的面积为________;
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?
一次函数与动点问题
学习任务五
5.2 一次函数与动直线、动图形问题
变式训练:如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止,设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.
(1)试写出y与x之间的函数表达式;
(2)当MA=4㎝时,重叠部分的面积是多少?
(3)当MA的长度是多少时,等腰直角△ABC与正方形MNPQ的重叠部分以外的四边形BCMD的面积与重叠部分的面积比为3:1?
(4)开始时等腰直角△ABC中A点与M点重合,已知△ABC向右移动的速度是1cm/s,在A点与N点重合后继续向右移动,当运动停止时边BC与PN重合,探究重叠部分的面积y( cm2?)与运动时间t(s)的函数表达式.
01
一次函数与选填运用
02
一次函数与面积问题
03
一次函数与实际问题
目录
04
一次函数与几何图形存在性问题
05
一次函数与动点问题
Part1 一次函数与选填运用
一次函数与选填运用
Part 1
一、一次函数补充知识点
1、一次函数的图象与性质
知识清单
一次函数与选填运用
Part 1
2、一次函数的特殊点
一次函数与x轴交点为(-bk,0),与y轴交点为(0,b),所以一次函数与y轴交点的纵坐标就是b的值.
3、k值
1)大小判断,当k>0时,一次函数图象与x轴夹角越大,k值越大;当k<0时,一次函数图象与x轴夹角越大,k值越小.
2)计算:设一次函数图象上有两点A(x1, y1?)、B( x2, y2?),则k=y1?y2x1?x2(要么分子分母前面都是y1?、x1?;要么分子分母前面都是y2?、x2?)
3)k值与特殊角:当k=±33时,一次函数与x轴夹角30°;当k=±1时,一次函数与x轴夹角45°;当k=±3时,一次函数与x轴夹角60°.
4)设两一次函数图象平行,则k1= k2?;两一次函数图象垂直,则k1 ?k2?=-1
?
一次函数与选填运用
Part 1
4、中点坐标公式:设坐标系中有两点A(x1, y1?)、B( x2, y2?),C为线段AB的中点,则C点坐标为(x1+x22,y1+y22?).
5、两点间距离公式:设坐标系中有两点A(x1, y1?)、B( x2, y2?),则:
AB=(x1?x2)2+(y1?y2)2
6、一元二次方程配方法求解
如:x2-4x+3=0→ x2-4x=-3 → x2-4x+4=-3+4 → (x?2)2=1 →x-2=±1 →x1=1+2=3x2=?1+2=1
?
知识清单
一次函数与选填运用
Part 1
1.1 一次函数与特殊点问题
例1、如图所示,直线y=k(x-2)+k+1与x轴、y轴分别交于B、C两点,且????????????????=12?.则k的值为( )
A. 13 B. 12
C.1 D.2
变式训练:在平面直角坐标系中,过点(1,2)作直线l,若直线l与两坐标轴围成的三角形面积为4,则满足条件的直线l的条数是( )
A.5 B.4 C.3 D.2
?
一次函数与选填运用
Part 1
1.2 一次函数与b取值范围问题
例2、如图,平面直角坐标系中,?????????????的顶点坐标分别是A(1,1),B(3,1),C(2,2),当直线y=12x+b与?????????????有交点时,b的取值范围是( )
A.?1≤b≤1 B. ?12≤b≤1
C. ?12≤b≤ 12 D. ?1≤b≤ 12
变式训练:如图,在平面直角坐标系中,菱形ABCD的顶点A、D的坐标分别为(﹣3,0)、(0,4),若直线y=﹣2x+b与菱形ABCD有公共点,则b的取值范围是( )
A.﹣6≤b≤4 B.4≤b≤8
C.﹣6≤b≤8 D.﹣6≤b≤14
?
一次函数与选填运用
Part 1
1.3 一次函数与k取值范围问题
例3、如图,已知直线????1:y=﹣2x+4与直线????2?:y=kx+b(k≠0)在第一象限交于点M.若直线????2与x轴的交点为A(﹣2,0),则k的取值范围是( )
A.﹣2<k<2 B.﹣2<k<0
C.0<k<4 D.0<k<2
变式训练:在平面直角坐标系中,点A(0,4),B(3,0),且四边形ABCD为正方形,若直线l:y=kx+4与线段BC有交点,则k的取值范围是( )
A.k≤43 B.﹣ 43 ≤k≤﹣17?
C.﹣ 43 ≤k≤﹣1 D.﹣ 43 ≤k≤ 43
?
一次函数与选填运用
Part 1
1.4 一次函数与平移问题
例4、如图,在平面直角坐标系中,点A(0,3),将△AOB沿x轴向右平移得到△A'O'B',与点A对应的点A'恰好在直线y=32x上,则BB'=_____.
变式训练:如图,△ABC的顶点坐标分别为A(1,0),B(4,0),C(1,4),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
A.4 B.8 C.82 D.16
?
一次函数与选填运用
Part 1
1.5 一次函数与翻折问题
例5、如图,直线y=-33x+2与x轴、y轴分别交于A、B两点,把△AOB沿直线AB翻折后得到△AO′B,则点O′的坐标是( )
A.(3,3) B.( 3?, 3?)
C.(2,2 3?) D.(2 3?,4)
变式训练:如图,直线y=-x+4分别与x轴,y轴交于A,B两点.从点P(2,0)射出的光线经直线AB反射后又经直线OB反射回到P点,则光线第一次的反射点Q的坐标是( )
A.(2,2) B.(2.5,1.5)
C.(3,1) D.(1.5,2.5)
?
一次函数与选填运用
Part 1
1.6 一次函数与不等式问题
例6、如图,已知一次函数y=kx+b(k,b为常数,且k≠0)的图象与x轴交于点A(3,0),若正比例函数y=mx(m为常数,且m≠0)的图象与一次函数的图象相交于点P,且点P的横坐标为1,则关于x的不等式(k-m)x+b<0的解集为( )
A.x<1 B.x>1
C. x<3 D. x>3
变式训练:如图所示,函数y1=x?和y2=13x+ 43的图象相交于(–1,1),(2,2)两点.当y1 > y2时,x的取值范围是( )
A.x<–1 B.x<–1或x>2
C.x>2 D.–1
一次函数与选填运用
Part 1
1.7 一次函数与面积问题
例7、如图,点A,B,C在一次函数y=-2x+m的图象上,它们的横坐标依次为 ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A.1 B.3 C.3(m-1) D.32(m-2)
变式训练:如图,在平面直角坐标系xoy中,直线l的解析式为y=-33+1,该直线与x轴、y轴分别交于点A、B,以AB为边在第一象限内作正△ABC.若点P(m,n)在第一象限内,且满足?????????????????=??????????????????,则n的取值范围是( )
A.0
一次函数与选填运用
Part 1
1.8 一次函数与最短路径问题
例8、如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(0,0) B.(-12?,- 12?)
C.(22?, -22?) D.( -22?, -22?)
变式训练:直线y=23?x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(-3,0) B.(-6,0)
C.(-52?,0) D.(- 32?,0)
?
一次函数与选填运用
Part 1
1.9 一次函数与图象分析问题
例9、在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
A.乙先出发的时间为0.5小时
B.甲的速度是80千米/小时
C.甲出发0.5小时后两车相遇
D.甲到B地比乙到A地早112?小时
?
一次函数与选填运用
Part 1
1.9 一次函数与图象分析问题
变式训练:如图,已知线段AB=12厘米,动点P以2厘米/秒的速度从点A出发向点B运动,动点Q以4厘米/秒的速度从点B出发向点A运动.两点同时出发,到达各自的终点后停止运动.设两点之间的距离为s(厘米),动点P的运动时间为t秒,则下图中能正确反映s与t之间的函数关系的是( )
A、 B、 C、 D、
一次函数与选填运用
Part 1
1.10 一次函数与规律探究问题
例10、如图,在平面直角坐标系中,直线l:y=33x+1交x轴于点A,交y轴于点B,点????1?、 ????2?、 ????3?,…在x轴的正半轴上,点????1?、 ????2?、 ????3?,…在直线l上.若△O ????1?????1?,△ ????1?????2?????2?,△ ????2?????3?????3?,…均为等边三角形,则△ ????6?????7?????7?的周长是______.
变式训练:如图,在平面直角坐标系中,点????1?、 ????2?、 ????3?…都在x轴上,点????1?、 ????2?、 ????3?…都在直线y=x上,O ????1?=1,且△ ????1?????1?????2?,△ ????2?????2?????3?,△ ????3 ????3?????4?,… ????n ????n?????n+1?…分别是以????1?、 ????2?、 ????3?,… ????n?…为直角顶点的等腰直角三角形,则△ ????10 ????10?????11?的面积是________.
?
一次函数与选填运用
Part 1
1.11 一次函数与其他
例11、已知k=a+b?cc?=a?b+cb =?a+b+ca,且m?5?+n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.
A.一、二 B.二、三 C.三、四 D.一、四
变式训练:如图,在直角坐标系中,等腰直角△ABO的O点是坐标原点,A的坐标是(﹣4,0),直角顶点B在第二象限,等腰直角△BCD的C点在y轴上移动,我们发现直角顶点D点随之在一条直线上移动,这条直线的解析式是( )
A.y=﹣2x+1 B.y=﹣12?x+2
C.y=﹣3x﹣2 D.y=﹣x+2
?
Part2 一次函数与面积问题
一次函数与面积问题
Part 2
1、面积问题常见分类
模型一:所有点均可求
A、B、C、D、E的坐标均可求,求?????????????????.
方法1:拆三角形
?????????????????= ?????????????????+ ?????????????????=12?BE?y????+ 12?BE?y????
方法2:补三角形
?????????????????= ?????????????????- ?????????????????= 12?AD?????????- 12?AD?????????
?
知识清单
一次函数与面积问题
Part 2
模型二:面积存在性问题
条件:A、O、B、C为定点(坐标可求),若点D在y轴
上,且满足?????????????????=13??????????????????,求D点坐标.
思路分析:此类问题一定有一个图形面积已知,通过该
图形的面积得出另一个图形的面积,另一个图形一定有
两个定点,一个动点,而且要么高是定值,要么底是定值.
详解: ?????????????????的值可求,所以可以通过等量关系求出?????????????????,因为?????????????的高为xc定值,所以OD长可求,设D点坐标为(0,m),则m?yo=OD,求解即可.
?
知识清单
一次函数与面积问题
Part 2
模型三:等面积找点
解题依据:利用两平行线之间的距离处处相等找点.
题目类型:A、B、C坐标已知,????为动点,?????????????????=?????????????????,且D点
过(m,52),则m的值为?
解题方法:求出直线AB的解析式,确定k值,因为C点坐标已
知,所以过C点的平行线也就可求解析式了,最后只需将D点
带入求出的过C点的平行线解析式就可求解出m的值.
?
知识清单
一次函数与面积问题
Part 2
2.1 模型一:拆补法求面积
例12:如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积.
一次函数与面积问题
Part 2
2.1 模型一:拆补法求面积
变式训练:如图,直线y=32?x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y= 32?x+m相交于点D,
(1)求D点的坐标;
(2)求四边形AOCD的面积;
?
一次函数与面积问题
Part 2
2.2 模型二:面积存在性问题
例13:如图,一次函数y=kx+b的图象经过点A(-2,6),且与x轴相交于点B,与正比例函数 y=3x的图象相交于点C,点C的横坐标为1.
(1)求一次函数y=kx+b的表达式;
(2)若点D在y轴负半轴上,且满足?????????????????=12??????????????????,求点D的坐标.
?
一次函数与面积问题
Part 2
2.2 模型二:面积存在性问题
变式训练:如图,在平面直角坐标系中,直线y=-x+6与x和y轴分别交于点B和点C,与直线OA相交于点A(4,2),动点M在线段OA和射线AC上运动.
①求点B和点C的坐标.
②求△OAC的面积.
③是否存在点M,使△OMC的面积是△OAC的面积的14??若存在,求出此时点M的坐标,若不存在,说明理由.
?
一次函数与面积问题
Part 2
2.3 模型三:等面积找点
例14:如图,在平面直角坐标系中,A(0,8),B(4,0),AB的垂直平分线交y轴与点D,连接BD,M(a,1)为第一象限内的点
(1)则D(____, ____),并求直线BD的解析式;
(2)当?????????????????=??????????????????时,求a的值;
?
一次函数与面积问题
Part 2
2.3 模型三:等面积找点
变式训练:如图,点A(1,0),B(0,3?)分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
(1)求直线AB的解析式及点C的坐标;
(2)若点P(m,32?)为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
?
Part3 一次函数与实际问题
一次函数与实际问题
学习任务三
3.1 分段函数
例15:赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)求甲、乙两支龙舟队之间的距离m与x的函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
一次函数与实际问题
学习任务三
3.1 分段函数
变式训练:都匀某校准备组织学生及家长代表到桂林进行社会实践活动,为便于管理,所有人员必须乘坐同一列高铁,高铁单程票价格如表所示,二等座学生票可打7.5折,已知所有人员都买一等座单程火车票需6175元,都买二等座单程火车票需3150元;如果家长代表与教师的人数之比为2:1.
(1)参加社会实践活动的老师、家长代表与学生各有多少人?
(2)由于各种原因,二等座单程火车票只能买x张(x<参加社会实践的总人数),其余的须买一等座单程火车票,在保证所有人员都有座位的前提下,请你设计最经济的购票方案,并写出购买单程火车票的总费用y与x之间的函数关系式.
(3)在(2)的方案下,请求出当x=30时,购买单程火车票的总费用.
一次函数与实际问题
学习任务三
3.2 不等式与函数增减性运用
例16:2017年遂宁市吹响了全国文明城市创建决胜“集结号”.为了加快创建步伐,某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方.已知一辆大型渣土运输车和一辆小型渣土运输车每次共运15吨;3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该渣土运输公司决定派出大小两种型号渣土运输车共20辆参与运输土方,若每次运输土方总量不小于148吨,且小型渣土运输车至少派出7辆,问该渣土运输公司有几种派出方案?
(3)在(2)的条件下,已知一辆大型渣土运输车运输话费500元/次,一辆小型渣土运输车运输花费300元/次,为了节约开支,该公司应选择哪种方案划算?
一次函数与实际问题
学习任务三
3.2 不等式与函数增减性运用
变式训练:为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
(1)求这15辆车中大小货车各多少辆?
(2)现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.
一次函数与实际问题
学习任务三
3.3 一次函数与最优方案问题
例17:某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A,B两种产品共50件.已知生产1件A种产品,需要甲种原料9kg,乙种原料3kg,可获利润700元;生产1件B种产品,需要甲种原料4kg,乙种原料10kg,可获利润1200元.
(1)按要求安排A,B两种产品的生产件数,有哪几种方案?请设计出来.
(2)设生产A,B两种产品所获总利润为y(元),其中一种产品的生产件数为x,试写出y关于x的函数解析式,并利用函数的性质说明(1)中哪种生产方案所获总利润最大,最大利润是多少.
一次函数与实际问题
学习任务三
3.3 一次函数与最优方案问题
变式训练:学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
一次函数与实际问题
学习任务三
3.4 一次函数与图象分析问题
例18:一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 x(h),两车之间的距离为 y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
(1)甲、乙两地之间的距离为______ km ;图中点 C 的实际意义为:______;慢车的速度为______,快车的速度为______;
(2)求线段 BC 所表示的 y 与 x 之间的函数关系式;(3)若在第一列快车与慢车相遇时,第二列快车从乙地出发驶往甲地,速度与第一列快车相同.求第二列快车出发多长时间,与慢车相距200km.
一次函数与实际问题
学习任务三
3.4 一次函数与图象分析问题
变式训练:甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量y(个)与加工时间x(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是_____,B点表示的实际意义是_____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
一次函数与实际问题
学习任务三
3.5 一次函数与参数问题
例19:某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)求y关于x的函数关系式;
(2)该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
一次函数与实际问题
学习任务三
3.5 一次函数与参数问题
变式训练:为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价180元,售价320元;乙种服装每件进价150元,售价280元.
(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?
(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0
一次函数与几何图形存在性问题
学习任务四
4.1 一次函数与全等三角形存在性问题
例20:如图,一次函数y=34x+6的图象与x,y轴分别交于A,B两点,点C与点A关于y轴对称.动点P,Q分别在线段AC,AB上(点P与点A,C不重合),且满足∠BPQ=∠BAO.
(1)求点A,B的坐标及线段BC的长度;
(2)当点P在什么位置时,?APQ≌?CBP,说明理由;
?
一次函数与几何图形存在性问题
学习任务四
4.1 一次函数与全等三角形存在性问题
变式训练:如图,直线y=-43x+4与x轴和y轴分别交于A、B两点,另一条直线过点A和点C(7,3).
(1)求直线AC的函数表达式;
(2)求证:AB⊥AC;
(3)若点P是直线AC上的一个动点,点Q是X轴上的一个动点,且以PQA为顶点的三角形与?????????????全等,求点Q的坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.2 一次函数与等腰三角形存在性问题
例21:如图,直线????1: y1?=﹣x+2与x轴,y轴分别交于A,B两点,点P(m,3)为直线????1上一点,另一直线????2?: y2?=12x+b过点P.
(1)求点P坐标和b的值;
(2)若点C是直线????2与x轴的交点,动点Q从点C开始以每秒1个单位的速度向x轴正方向移动.设点Q的运动时间为t秒.
①请写出当点Q在运动过程中,△APQ的面积S与t的函数关系式;
②求出t为多少时,△APQ的面积小于3;
③是否存在t的值,使△APQ为等腰三角形?若存在,请求出t的值;若不存在,请说明理由.
?
一次函数与几何图形存在性问题
学习任务四
4.2 一次函数与等腰三角形存在性问题
变式训练:一次函数y=﹣33?x+1的图象与x轴、y轴分别交于点A、B,以AB为边在第一象限内做等边△ABC.
(1)求△ABC的面积和点C的坐标;
(2)如果在第二象限内有一点P(a,12?),试用含a的代数式表示四边形ABPO的面积.
(3)在x轴上是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
?
一次函数与几何图形存在性问题
学习任务四
4.3 一次函数与直角三角形存在性问题
例22:如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M在y轴上运动.
(1)求直线AB的函数解析式;
(2)动点M在y轴上运动,使MA+MB的值最小,求点M的坐标;
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求出点M的坐标;如果不存在,说明理由.
一次函数与几何图形存在性问题
学习任务四
4.3 一次函数与直角三角形存在性问题
变式训练:如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)在y轴的负半轴上是否存在点M,使△ABM是以AB为直角边的直角角形?如果存在,求出点M的坐标;如果不存在,说明理由.
一次函数与几何图形存在性问题
学习任务四
4.4 一次函数与等腰直角三角形存在性问题
例23:(1)如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于点D,过B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(模型应用)
(2)①已知直线????1?:y=43x+4与坐标轴交于点A、B,将直线????1绕点A逆时针旋转45°至直线????2?,如图2,求直线????2的函数表达式;
②如图3,长方形ABCO,O为坐标原点,点B的坐标为(8,-6),点A、C分别在坐标轴上,点P是线段BC上的动点,点D是直线y=-2x+6上的动点且在第四象限.若△APD是以点D为直角顶点的等腰直角三角形,请直接写出点D的坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.4 一次函数与等腰直角三角形存在性问题
变式训练:如图,在平面直角坐标系中,直线????1的解析式为y=-x,直线????2与????1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+b+3=0.
(1)求直线????2的解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与????1?, ????2交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.5 一次函数与平行四边形存在性问题
例24:如图,已知函数y=-13?x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点E,点E的横坐标为3.
(1)求点A的坐标;
(2)在x轴上有一点F(a,0),过点F作x轴的垂线,分别交函数y=- 13?x+b和y=x的图象于点C、D,若以点B、O、C、D为顶点的四边形为平行四边形,求a的值.
?
一次函数与几何图形存在性问题
学习任务四
4.5 一次函数与平行四边形存在性问题
变式训练:如图,在平面直角坐标系中,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,线段OA,OC的长分别是m,n且满足(?????6)2+?????8=0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处.
(1)求线段OD的长
(2)求点E的坐标
(3)DE所在直线与AB相交于点M,点N在x轴的正半轴上,以M、A、N、C为顶点的四边形是平行四边形时,求N点坐标.
?
一次函数与几何图形存在性问题
学习任务四
4.6 一次函数与菱形存在性问题
例25:如图,在平面直角坐标系中,点O为坐标原点,直线l分别交x轴、y轴于A、B两点,AB=5,OA:OB =3:4.
(1)求直线l的表达式;
(2)点P是y轴上的点,点Q是第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q点的坐标.
一次函数与几何图形存在性问题
学习任务四
4.6 一次函数与菱形存在性问题
变式训练:如图,在平面直角坐标系中,直线????1?:y=-12x+6分别与x轴、y轴交于点B、C,且与直线????2?: y= 12x交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.
?
一次函数与几何图形存在性问题
学习任务四
4.7 一次函数与正方形存在性问题
例26:如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2,1).
(1)求k,b的值;
(2)P为直线AB上一点,PC⊥x轴于点C,PD⊥y轴于点D,若四边形PCOD为正方形,求点P的坐标.
一次函数与几何图形存在性问题
学习任务四
4.7 一次函数与正方形存在性问题
变式训练:如图,已知一次函数y=﹣12?x+b的图象过点A(0,3),点p是该直线上的一个动点,过点P分别作PM垂直x轴于点M,PN垂直y轴于点N,在四边形PMON上分别截取:PC=13?MP,MB= 13?OM,OE= 13?ON,ND= 13?NP.
(1)求b的值;
(2)求证:四边形BCDE是平行四边形;
(3)在直线y=﹣ 12?x+b上是否存在这样的点P,使四边形BCDE为正方形?若存在,请求出所有符合的点P的坐标;若不存在,请说明理由.
?
Part5 一次函数与动点问题
一次函数与动点问题
学习任务五
5.1 一次函数与动点问题
例27:已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.
(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
一次函数与动点问题
学习任务五
5.1 一次函数与动点问题
变式训练:在矩形ABCD中AB=16,AD=12,点M是AD的中点,点N是CD的中点,点P从A点出发沿A→B→C→D的路线匀速运动,速度为2单位长度/秒,点Q从N点出发沿N→C→B→A的路线匀速运动,速度为1单位长度/秒,P、Q两点同时运动,时间为t秒,若其中一点到达终点,另一点也随即停止运动.
(1)如图1,若矩形ABCD与∠PMA重叠部分的面积为y.
①求当t=4,10,16时,y的值.
②求y关于t的函数解析式.
(2)当以M、D、P、Q四个点为顶点的四边形是平行四边形时,求出此时t的值.
一次函数与动点问题
学习任务五
5.2 一次函数与动直线、动图形问题
例28:如图,直线y=4-x与两坐标轴分别相交于A、B点,点M是线段AB上任意一点(A、B两点除外),过M分别作MC⊥OA于点C,MD⊥OB于点D.
(1)当点M在AB上运动时,四边形OCMD的周长为________;
(2)当四边形OCMD为正方形时,将正方形OCMD沿着x轴的正方向移动,设平移的距离为a (0
②当平移距离a是多少时,正方形OCMD的面积被直线AB分成l:3两个部分?
一次函数与动点问题
学习任务五
5.2 一次函数与动直线、动图形问题
变式训练:如图,等腰直角△ABC(∠C=90°)的直角边长与正方形MNPQ的边长均为6cm,CA与MN在同一直线上,开始时A点与M点重合,让△ABC向右平移,直到C点与M点重合时为止,设△ABC与正方形MNPQ的重叠部分(图中阴影部分)的面积为ycm2,MA的长度为xcm.
(1)试写出y与x之间的函数表达式;
(2)当MA=4㎝时,重叠部分的面积是多少?
(3)当MA的长度是多少时,等腰直角△ABC与正方形MNPQ的重叠部分以外的四边形BCMD的面积与重叠部分的面积比为3:1?
(4)开始时等腰直角△ABC中A点与M点重合,已知△ABC向右移动的速度是1cm/s,在A点与N点重合后继续向右移动,当运动停止时边BC与PN重合,探究重叠部分的面积y( cm2?)与运动时间t(s)的函数表达式.
