人教版八年级下册18.1.2平行四边形的判定(第1课时)课件(共20张PPT)
文档属性
| 名称 | 人教版八年级下册18.1.2平行四边形的判定(第1课时)课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:36:05 | ||
图片预览


文档简介
人教版八年级数学
第十八章 平行四边形
18.1.2平行四边形的判定(第1课时)
课标解读
1.掌握平行四边形的定义判定以及其它边,角,对角线等判定方法
2.根据题目要求,不能混淆或臆造出平行四边形的判定,灵活选择恰当方法,做到有的放矢。
知识梳理:平行四边形的判定
1.边
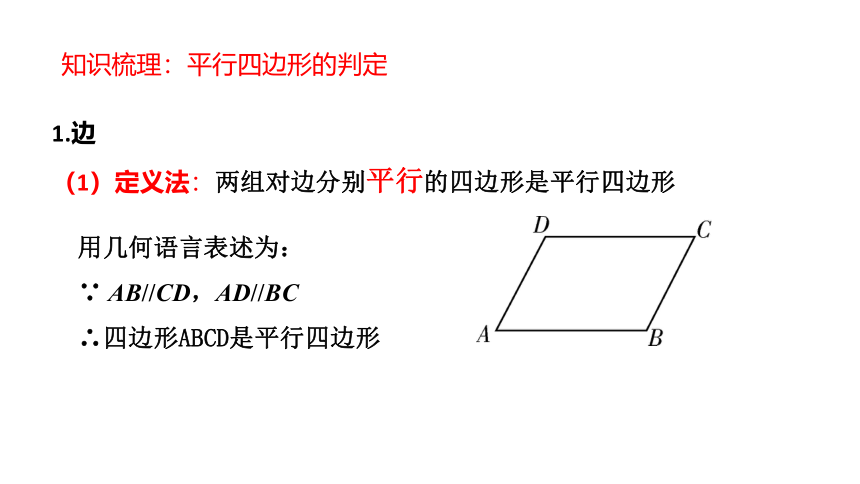
(1)定义法:两组对边分别平行的四边形是平行四边形
用几何语言表述为:
∵ AB//CD,AD//BC
∴四边形ABCD是平行四边形
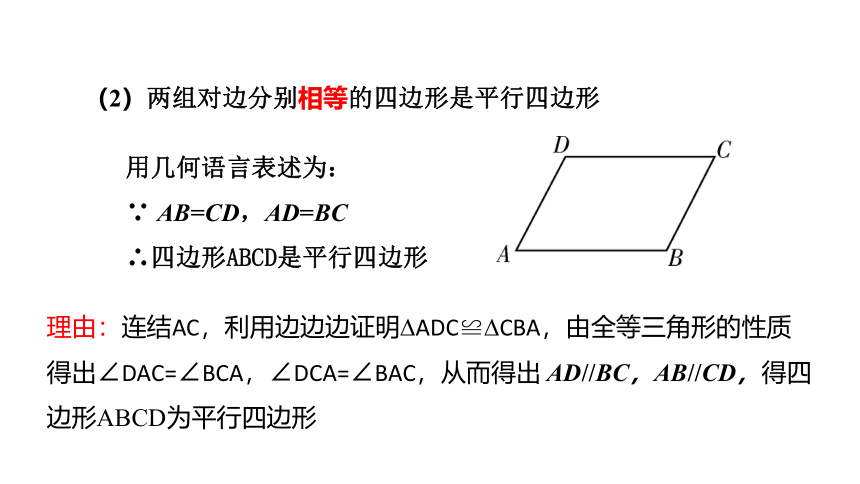
(2)两组对边分别相等的四边形是平行四边形
用几何语言表述为:
∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
理由:连结AC,利用边边边证明?ADC≌?CBA,由全等三角形的性质得出∠DAC=∠BCA,∠DCA=∠BAC,从而得出 AD//BC,AB//CD,得四边形ABCD为平行四边形
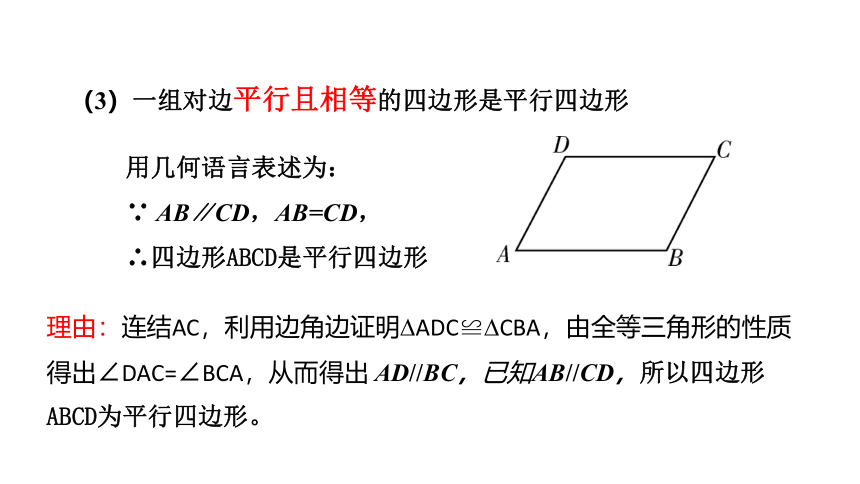
(3)一组对边平行且相等的四边形是平行四边形
用几何语言表述为:
∵ AB∥CD,AB=CD,
∴四边形ABCD是平行四边形
理由:连结AC,利用边角边证明?ADC≌?CBA,由全等三角形的性质得出∠DAC=∠BCA,从而得出 AD//BC,已知AB//CD,所以四边形ABCD为平行四边形。
2.角
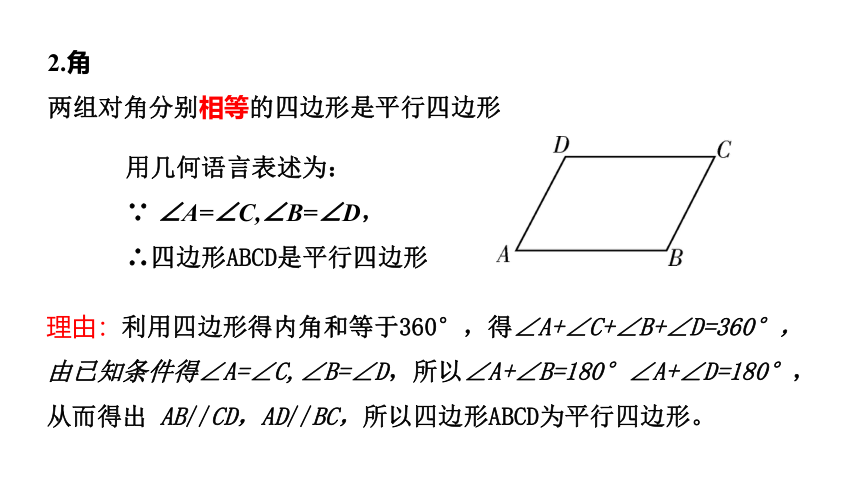
两组对角分别相等的四边形是平行四边形
用几何语言表述为:
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形
理由:利用四边形得内角和等于360°,得∠A+∠C+∠B+∠D=360°,由已知条件得∠A=∠C,∠B=∠D,所以∠A+∠B=180°∠A+∠D=180°,从而得出 AB//CD,AD//BC,所以四边形ABCD为平行四边形。
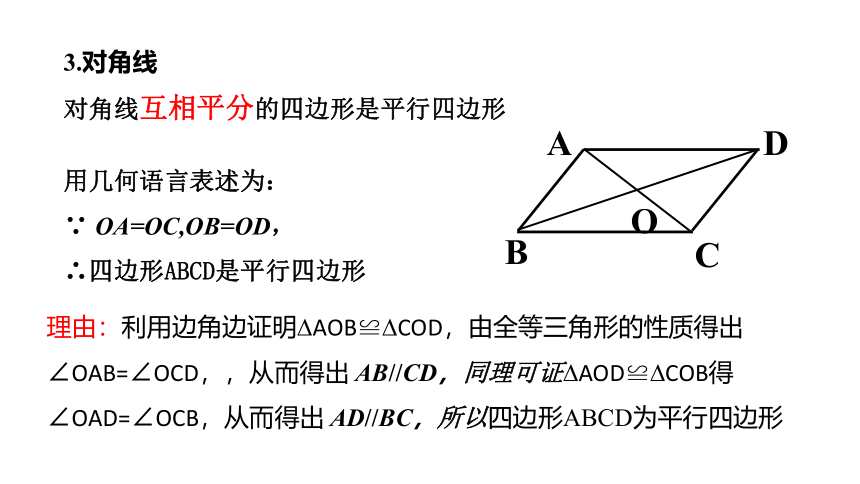
3.对角线
对角线互相平分的四边形是平行四边形
用几何语言表述为:
∵ OA=OC,OB=OD,
∴四边形ABCD是平行四边形
B
A
D
C
O
理由:利用边角边证明?AOB≌?COD,由全等三角形的性质得出∠OAB=∠OCD,,从而得出 AB//CD,同理可证?AOD≌?COB得∠OAD=∠OCB,从而得出 AD//BC,所以四边形ABCD为平行四边形
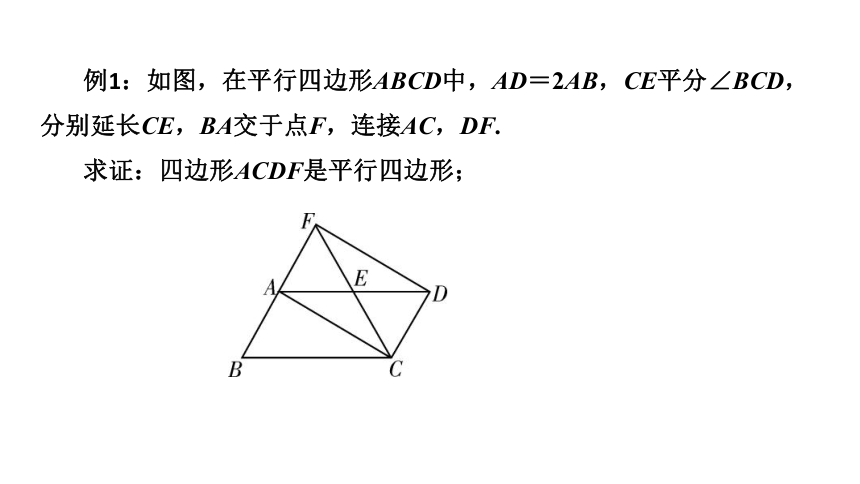
例1:如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD,分别延长CE,BA交于点F,连接AC,DF. 求证:四边形ACDF是平行四边形;
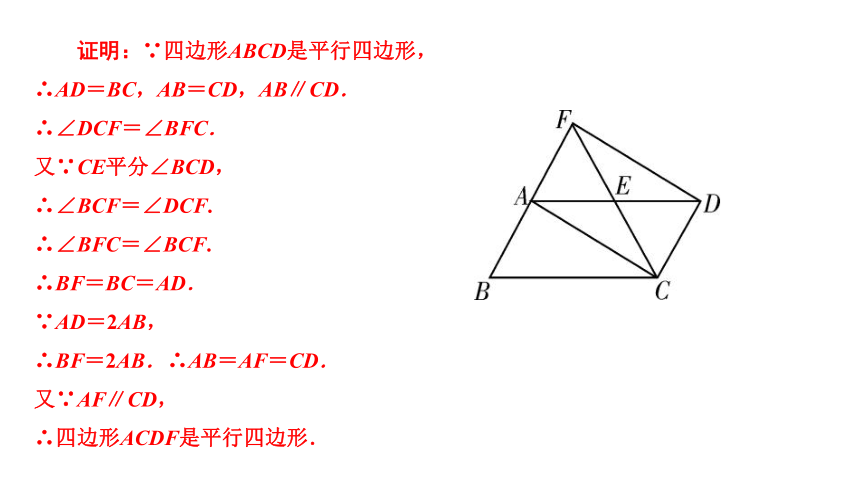
证明:∵四边形ABCD是平行四边形, ∴AD=BC,AB=CD,AB∥CD. ∴∠DCF=∠BFC. 又∵CE平分∠BCD, ∴∠BCF=∠DCF. ∴∠BFC=∠BCF. ∴BF=BC=AD. ∵AD=2AB, ∴BF=2AB.∴AB=AF=CD. 又∵AF∥CD, ∴四边形ACDF是平行四边形.
归纳总结: 证明一个四边形是平行四边形,往往有多种证明思路,因此必须仔细分析,通过比较,选择最简捷的证明思路,方法如下: (1)已知一组对边相等——①证另一组对边相等;②证这组对边平行. (2)已知一组对边平行——①证另一组对边平行;②证这组对边相等. (3)已知一组对角相等——证另一组对角相等. (4)若图中有对角线——证对角线互相平分.
例2.已知:如图,在?ABCD中,点E,F分别是边AD,BC的中点.求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC. ∵点E,F分别是边AD,BC的中点, ∴DE=1/2AD,BF=1/2BC. ∴DE=BF. 又∵DE∥BF, ∴四边形BFDE是平行四边形. ∴BE=DF.
例3.如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连接AE交CD于点F,且F是CD的中点.
求证:(1)△ADF≌△ECF; (2)四边形ABCD是平行四边形.
证明:(1)∵AD∥BC, ∴∠DAF=∠E. ∵F是CD的中点, ∴DF=CF. 又∵∠AFD=∠EFC, ∴△ADF≌△ECF(AAS). (2)∵△ADF≌△ECF, ∴AD=EC. 又∵CE=BC, ∴AD=BC. 又∵AD∥BC, ∴四边形ABCD是平行四边形.
1.如图,在四边形ABCD中,AD=BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形.
同步练习
AD∥BC或AB=CD
2. 如图,四边形ABCD的对角线AC,BD相交于点O. (1)已知AD∥BC,可添加条件_______________________________,使四边形ABCD为平行四边形; (2)已知OA=OC,可添加条件___________________________,使四边形ABCD为平行四边形.
AB∥CD或AD=BC(答案不唯一)
BO=DO(答案不唯一)
3.如图,在?ABCD中,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点 求证:四边形EFGH是平行四边形
证明:在?ABCD中,OA=OC,OB=OD,
∵E,F,G,H分别是AO,BO,CO,DO的中点
∴OE=1/2OA,OG=1/2OC,OF=1/2OB,OH=1/2OD
∴OE=OG,OF=OH
∴四边形EFGH是平行四边形
1.如图,E是?ABCD的边AD延长线上一点,连接BE,CE,BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( ) A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
C
拓展提升
2.△ABC是等腰三角形,AB=AC, P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.求证:PE+PF=AB.
A
B
C
E
F
P
温馨提示:先证明四边形AFPE是平行四边形,由平行四边形得性质得AE=PF,AF=PE,从而得PE+PF=AB
3.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
答案:DE=20cm,∠D=60°
第十八章 平行四边形
18.1.2平行四边形的判定(第1课时)
课标解读
1.掌握平行四边形的定义判定以及其它边,角,对角线等判定方法
2.根据题目要求,不能混淆或臆造出平行四边形的判定,灵活选择恰当方法,做到有的放矢。
知识梳理:平行四边形的判定
1.边
(1)定义法:两组对边分别平行的四边形是平行四边形
用几何语言表述为:
∵ AB//CD,AD//BC
∴四边形ABCD是平行四边形
(2)两组对边分别相等的四边形是平行四边形
用几何语言表述为:
∵ AB=CD,AD=BC
∴四边形ABCD是平行四边形
理由:连结AC,利用边边边证明?ADC≌?CBA,由全等三角形的性质得出∠DAC=∠BCA,∠DCA=∠BAC,从而得出 AD//BC,AB//CD,得四边形ABCD为平行四边形
(3)一组对边平行且相等的四边形是平行四边形
用几何语言表述为:
∵ AB∥CD,AB=CD,
∴四边形ABCD是平行四边形
理由:连结AC,利用边角边证明?ADC≌?CBA,由全等三角形的性质得出∠DAC=∠BCA,从而得出 AD//BC,已知AB//CD,所以四边形ABCD为平行四边形。
2.角
两组对角分别相等的四边形是平行四边形
用几何语言表述为:
∵ ∠A=∠C,∠B=∠D,
∴四边形ABCD是平行四边形
理由:利用四边形得内角和等于360°,得∠A+∠C+∠B+∠D=360°,由已知条件得∠A=∠C,∠B=∠D,所以∠A+∠B=180°∠A+∠D=180°,从而得出 AB//CD,AD//BC,所以四边形ABCD为平行四边形。
3.对角线
对角线互相平分的四边形是平行四边形
用几何语言表述为:
∵ OA=OC,OB=OD,
∴四边形ABCD是平行四边形
B
A
D
C
O
理由:利用边角边证明?AOB≌?COD,由全等三角形的性质得出∠OAB=∠OCD,,从而得出 AB//CD,同理可证?AOD≌?COB得∠OAD=∠OCB,从而得出 AD//BC,所以四边形ABCD为平行四边形
例1:如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD,分别延长CE,BA交于点F,连接AC,DF. 求证:四边形ACDF是平行四边形;
证明:∵四边形ABCD是平行四边形, ∴AD=BC,AB=CD,AB∥CD. ∴∠DCF=∠BFC. 又∵CE平分∠BCD, ∴∠BCF=∠DCF. ∴∠BFC=∠BCF. ∴BF=BC=AD. ∵AD=2AB, ∴BF=2AB.∴AB=AF=CD. 又∵AF∥CD, ∴四边形ACDF是平行四边形.
归纳总结: 证明一个四边形是平行四边形,往往有多种证明思路,因此必须仔细分析,通过比较,选择最简捷的证明思路,方法如下: (1)已知一组对边相等——①证另一组对边相等;②证这组对边平行. (2)已知一组对边平行——①证另一组对边平行;②证这组对边相等. (3)已知一组对角相等——证另一组对角相等. (4)若图中有对角线——证对角线互相平分.
例2.已知:如图,在?ABCD中,点E,F分别是边AD,BC的中点.求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC. ∵点E,F分别是边AD,BC的中点, ∴DE=1/2AD,BF=1/2BC. ∴DE=BF. 又∵DE∥BF, ∴四边形BFDE是平行四边形. ∴BE=DF.
例3.如图,在四边形ABCD中,AD∥BC,延长BC到点E,使CE=BC,连接AE交CD于点F,且F是CD的中点.
求证:(1)△ADF≌△ECF; (2)四边形ABCD是平行四边形.
证明:(1)∵AD∥BC, ∴∠DAF=∠E. ∵F是CD的中点, ∴DF=CF. 又∵∠AFD=∠EFC, ∴△ADF≌△ECF(AAS). (2)∵△ADF≌△ECF, ∴AD=EC. 又∵CE=BC, ∴AD=BC. 又∵AD∥BC, ∴四边形ABCD是平行四边形.
1.如图,在四边形ABCD中,AD=BC,在不添加任何辅助线的情况下,请你添加一个条件 ,使四边形ABCD是平行四边形.
同步练习
AD∥BC或AB=CD
2. 如图,四边形ABCD的对角线AC,BD相交于点O. (1)已知AD∥BC,可添加条件_______________________________,使四边形ABCD为平行四边形; (2)已知OA=OC,可添加条件___________________________,使四边形ABCD为平行四边形.
AB∥CD或AD=BC(答案不唯一)
BO=DO(答案不唯一)
3.如图,在?ABCD中,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点 求证:四边形EFGH是平行四边形
证明:在?ABCD中,OA=OC,OB=OD,
∵E,F,G,H分别是AO,BO,CO,DO的中点
∴OE=1/2OA,OG=1/2OC,OF=1/2OB,OH=1/2OD
∴OE=OG,OF=OH
∴四边形EFGH是平行四边形
1.如图,E是?ABCD的边AD延长线上一点,连接BE,CE,BD,BE交CD于点F.添加以下条件,不能判定四边形BCED为平行四边形的是( ) A.∠ABD=∠DCE B.DF=CF C.∠AEB=∠BCD D.∠AEC=∠CBD
C
拓展提升
2.△ABC是等腰三角形,AB=AC, P是底边BC上一动点,PE∥AB,PF∥AC,点E,F分别在AC,AB上.求证:PE+PF=AB.
A
B
C
E
F
P
温馨提示:先证明四边形AFPE是平行四边形,由平行四边形得性质得AE=PF,AF=PE,从而得PE+PF=AB
3.有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?
答案:DE=20cm,∠D=60°
