人教版八年级下册18.1平行四边形的性质课件(共21张PPT)
文档属性
| 名称 | 人教版八年级下册18.1平行四边形的性质课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 499.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:37:10 | ||
图片预览



文档简介
人教版八年级数学
第十八章 平行四边形
18.1.1平行四边形的性质
课标解读:
1.理解平行四边形的概念,了解四边形的不稳定性.
2.从边,角,对角线,对称性等方面掌握平行四边形的性质.
3.了解两条平行线之间距离的意义,能度量两条平行线之间的距离.
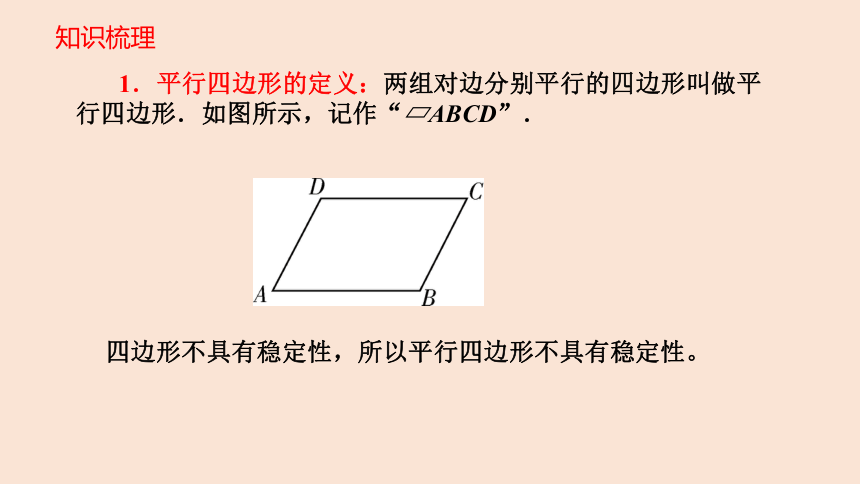
1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.如图所示,记作“?ABCD”.
四边形不具有稳定性,所以平行四边形不具有稳定性。
知识梳理
2.平行四边形的性质
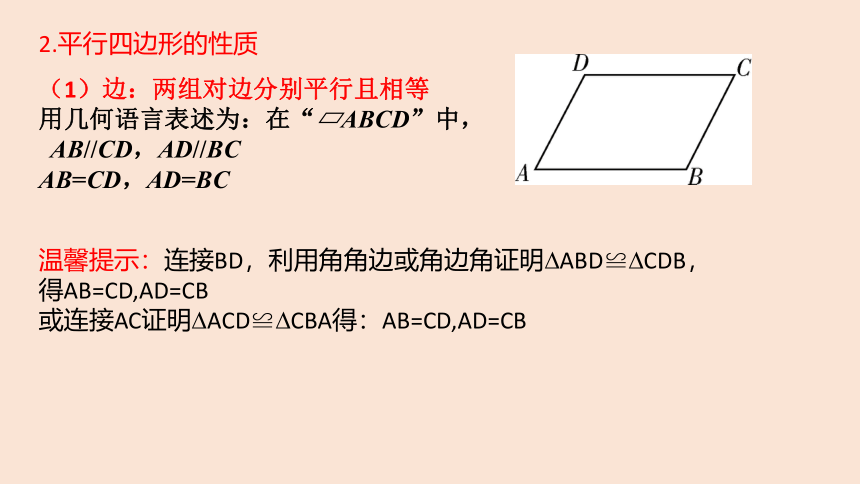
(1)边:两组对边分别平行且相等
用几何语言表述为:在“?ABCD”中,
AB//CD,AD//BC
AB=CD,AD=BC
温馨提示:连接BD,利用角角边或角边角证明?ABD≌?CDB,
得AB=CD,AD=CB
或连接AC证明?ACD≌?CBA得:AB=CD,AD=CB
(2)角:两组对角分别相等,邻角互补
用几何语言表述为:在“?ABCD”中,
∠BAD=∠BCD,∠ABC=∠ADC
∠ABC+∠BCD=180°,∠BCD+∠ADC=180°,
∠CDA+∠DAB=180°,∠DAB+∠ABC=180°
温馨提示:方法一:连接BD,利用角角边或角边角证明?ABD≌?CDB得:∠A=∠C,∠DAB=∠ABC
方法二:利用平行线性质得∠A+∠D=180°∠A+∠B=180°,因为同角的补角相等得:∠D=∠B,同理得∠A=∠C
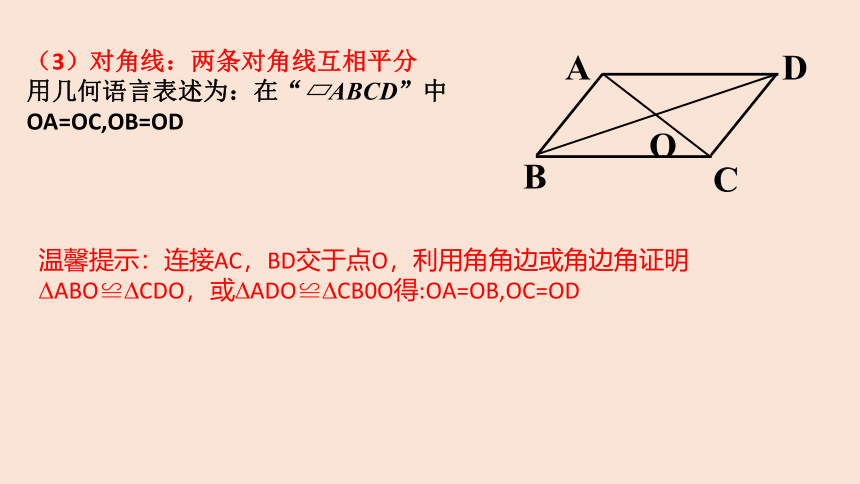
(3)对角线:两条对角线互相平分
用几何语言表述为:在“?ABCD”中 OA=OC,OB=OD
B
A
D
C
O
温馨提示:连接AC,BD交于点O,利用角角边或角边角证明?ABO≌?CDO,或?ADO≌?CB0O得:OA=OB,OC=OD
B
A
D
C
O
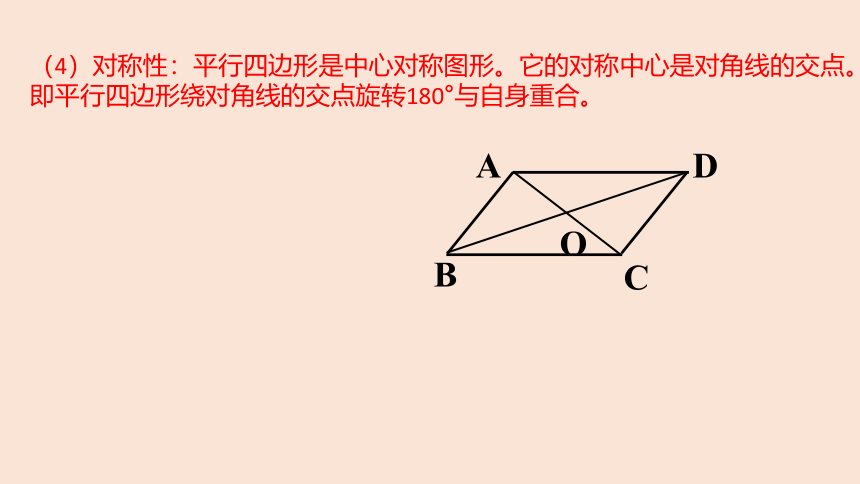
(4)对称性:平行四边形是中心对称图形。它的对称中心是对角线的交点。
即平行四边形绕对角线的交点旋转180°与自身重合。
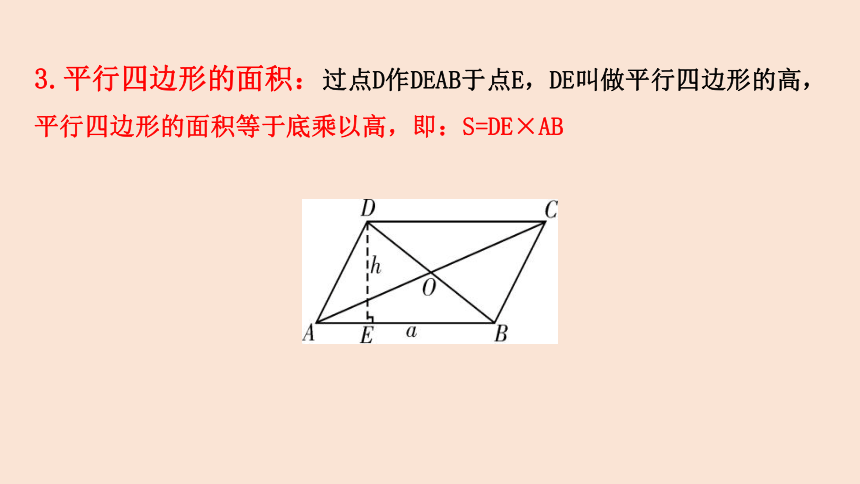
3.平行四边形的面积:过点D作DEAB于点E,DE叫做平行四边形的高,
平行四边形的面积等于底乘以高,即:S=DE×AB
性质:平行线之间的距离处处相等.
A
B
C
D
b
a
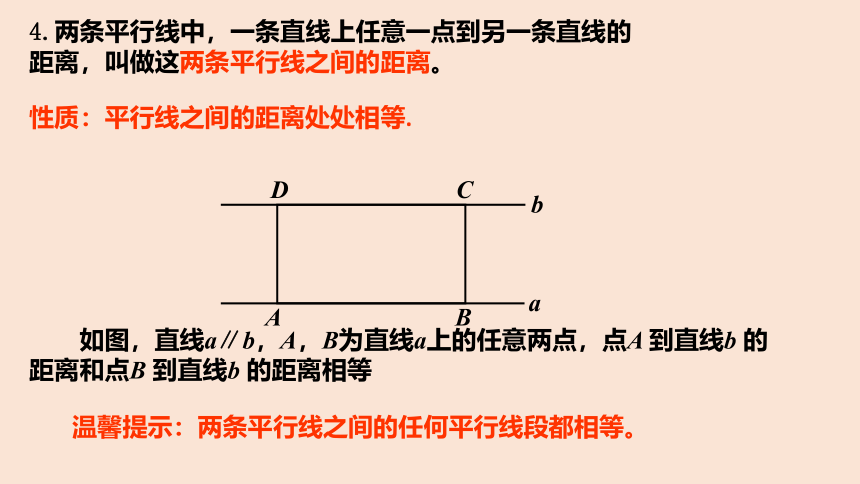
如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等
4.两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
温馨提示:两条平行线之间的任何平行线段都相等。
1.有关四边形的问题常常转化为三角形问题解决;
2.平行四边形的一条对角线把平行四边形分成两个全等的三角形,两条对角把平行四边形分为四个面积相等的三角形
方法指导:
例1:如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F。求证AE=CF.
证明:∵四边形ABCD为平行四边形
∴∠A=∠C,AD=CB
又∵∠AED=∠CFB=90°
∴△ADE≌△CBF
∴AE=CF
A
B
C
D
E
F
A
D
B
C
40
1.在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= ∠D=
30
120°
120°
60°
2.在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
A
B
C
D
120°
40°
巩固练习
6、如果平行四边行中有两个内角的度数 比为1:2,你能求出这个平行四边形的每个内角的度数吗?
5、在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
4、在?ABCD中, ∠B的平分线BE交AD于E,BC=5,AB=3,则ED的长为 。
2
D
60、120、60、120
°
°
°
°
例2:如图,在 ABCD中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及 ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是平行四边形
∴ BC=AD=8,CD=AB=10
∵ AC ⊥ BD
∴ △ ABC是直角三角形
在Rt △ ABC中,根据勾股定理得:AC2=AB2-BC2
∴AC2=102-82=36,即AC=6
又OA=OC
OA=1/2AC=3
平行四边形ABCD的面积为6 × 8=48
E
F
图中还有哪些量相等?
变式 在上题中,直线EF过点O,且与AB,CD分
别相交于点E,F.求证:OE=OF.
A
B
C
D
O
1.如图:在 ? ABCD中,BC=10,AC=8,BD=14,?AOD的周长是多少?为什么??ABC与 ?DBC的周长哪个长?
A
B
C
D
O
巩固练习
2.如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:∠BAE=∠DCF。
A
B
C
D
E
F
温馨提示:证?ABE≌?CDF
1.(2019·梧州)如图,在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= 度.
61
拓展提升
2.(2019·达州)如图,?ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16
3.(2019·遂宁)如图,在?ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若?ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
D
第十八章 平行四边形
18.1.1平行四边形的性质
课标解读:
1.理解平行四边形的概念,了解四边形的不稳定性.
2.从边,角,对角线,对称性等方面掌握平行四边形的性质.
3.了解两条平行线之间距离的意义,能度量两条平行线之间的距离.
1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.如图所示,记作“?ABCD”.
四边形不具有稳定性,所以平行四边形不具有稳定性。
知识梳理
2.平行四边形的性质
(1)边:两组对边分别平行且相等
用几何语言表述为:在“?ABCD”中,
AB//CD,AD//BC
AB=CD,AD=BC
温馨提示:连接BD,利用角角边或角边角证明?ABD≌?CDB,
得AB=CD,AD=CB
或连接AC证明?ACD≌?CBA得:AB=CD,AD=CB
(2)角:两组对角分别相等,邻角互补
用几何语言表述为:在“?ABCD”中,
∠BAD=∠BCD,∠ABC=∠ADC
∠ABC+∠BCD=180°,∠BCD+∠ADC=180°,
∠CDA+∠DAB=180°,∠DAB+∠ABC=180°
温馨提示:方法一:连接BD,利用角角边或角边角证明?ABD≌?CDB得:∠A=∠C,∠DAB=∠ABC
方法二:利用平行线性质得∠A+∠D=180°∠A+∠B=180°,因为同角的补角相等得:∠D=∠B,同理得∠A=∠C
(3)对角线:两条对角线互相平分
用几何语言表述为:在“?ABCD”中 OA=OC,OB=OD
B
A
D
C
O
温馨提示:连接AC,BD交于点O,利用角角边或角边角证明?ABO≌?CDO,或?ADO≌?CB0O得:OA=OB,OC=OD
B
A
D
C
O
(4)对称性:平行四边形是中心对称图形。它的对称中心是对角线的交点。
即平行四边形绕对角线的交点旋转180°与自身重合。
3.平行四边形的面积:过点D作DEAB于点E,DE叫做平行四边形的高,
平行四边形的面积等于底乘以高,即:S=DE×AB
性质:平行线之间的距离处处相等.
A
B
C
D
b
a
如图,直线a∥b,A,B为直线a上的任意两点,点A 到直线b 的距离和点B 到直线b 的距离相等
4.两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
温馨提示:两条平行线之间的任何平行线段都相等。
1.有关四边形的问题常常转化为三角形问题解决;
2.平行四边形的一条对角线把平行四边形分成两个全等的三角形,两条对角把平行四边形分为四个面积相等的三角形
方法指导:
例1:如图,在?ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F。求证AE=CF.
证明:∵四边形ABCD为平行四边形
∴∠A=∠C,AD=CB
又∵∠AED=∠CFB=90°
∴△ADE≌△CBF
∴AE=CF
A
B
C
D
E
F
A
D
B
C
40
1.在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= ∠D=
30
120°
120°
60°
2.在 ABCD 中,∠ADC=120°, ∠CAD=20°,则∠ABC= , ∠CAB=
A
B
C
D
120°
40°
巩固练习
6、如果平行四边行中有两个内角的度数 比为1:2,你能求出这个平行四边形的每个内角的度数吗?
5、在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
A.1:2:3:4 B.1:2:2:1
C.1:1:2:2 D.2:1:2:1
4、在?ABCD中, ∠B的平分线BE交AD于E,BC=5,AB=3,则ED的长为 。
2
D
60、120、60、120
°
°
°
°
例2:如图,在 ABCD中,AB=10,AD=8,AC⊥BC.
求BC,CD,AC,OA的长,以及 ABCD的面积.
A
B
C
D
O
解:∵四边形ABCD是平行四边形
∴ BC=AD=8,CD=AB=10
∵ AC ⊥ BD
∴ △ ABC是直角三角形
在Rt △ ABC中,根据勾股定理得:AC2=AB2-BC2
∴AC2=102-82=36,即AC=6
又OA=OC
OA=1/2AC=3
平行四边形ABCD的面积为6 × 8=48
E
F
图中还有哪些量相等?
变式 在上题中,直线EF过点O,且与AB,CD分
别相交于点E,F.求证:OE=OF.
A
B
C
D
O
1.如图:在 ? ABCD中,BC=10,AC=8,BD=14,?AOD的周长是多少?为什么??ABC与 ?DBC的周长哪个长?
A
B
C
D
O
巩固练习
2.如图,平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.
求证:∠BAE=∠DCF。
A
B
C
D
E
F
温馨提示:证?ABE≌?CDF
1.(2019·梧州)如图,在?ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,则∠BHF= 度.
61
拓展提升
2.(2019·达州)如图,?ABCD的对角线AC,BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为 .
16
3.(2019·遂宁)如图,在?ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE.若?ABCD的周长为28,则△ABE的周长为( )
A.28 B.24 C.21 D.14
D
