人教版八年级下册19.2.2 一次函数(2)课件(24张PPT)
文档属性
| 名称 | 人教版八年级下册19.2.2 一次函数(2)课件(24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 21:57:57 | ||
图片预览







文档简介
八年级 下册
19.2.2 一次函数(2)
学习目标:
1.会画一次函数的图象;
2.能从图象角度理解正比例函数与一次函数的关
系;
3.能根据一次函数的图象和表达式y =kx+b(k≠0)
理解k>0和k<0时,图象的变化情况. 从而理
解一次函数的增减性;
(1)什么叫正比例函数?从解析式看,正比例函
数与一次函数有什么关系?
(2)正比例函数有哪些性质?是怎样得到这些性
质的?
想一想
正比例函数的图像和性质
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线。 它们图象之间有什么关系?一次函数的又有什么性质呢?
研究函数 y =kx+b(k≠0)的性质;
研究方法:
画图象→观察图象→变量(坐标)意义解释.
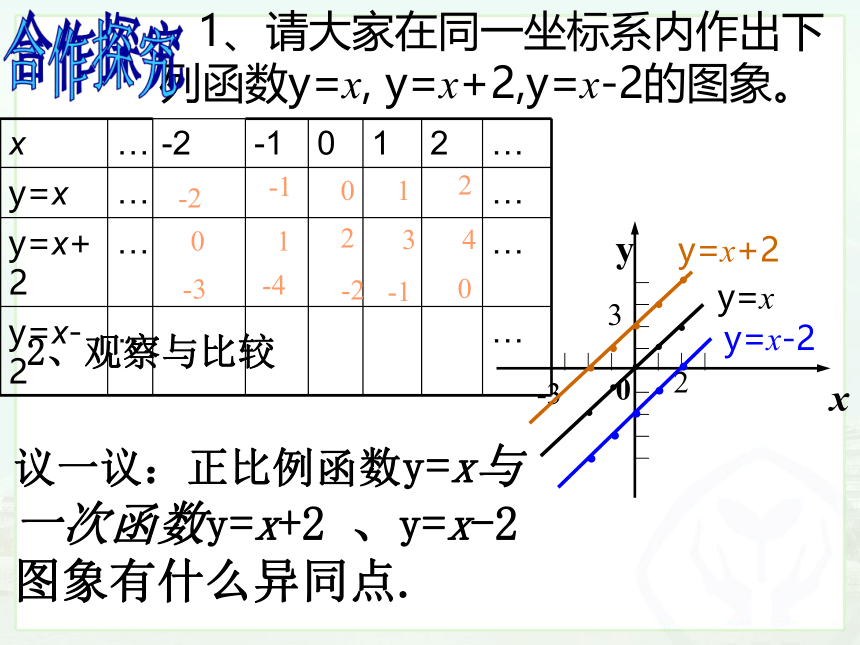
1、请大家在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象。
x
…
-2
-1
0
1
2
…
y=x
…
…
y=x+2
…
…
y=x-2
…
…
-2
0
-4
-1
1
-3
0
2
-2
1
3
-1
2
4
0
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
议一议:正比例函数y=x与一次函数y=x+2 、y=x-2图象有什么异同点.
2、观察与比较
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
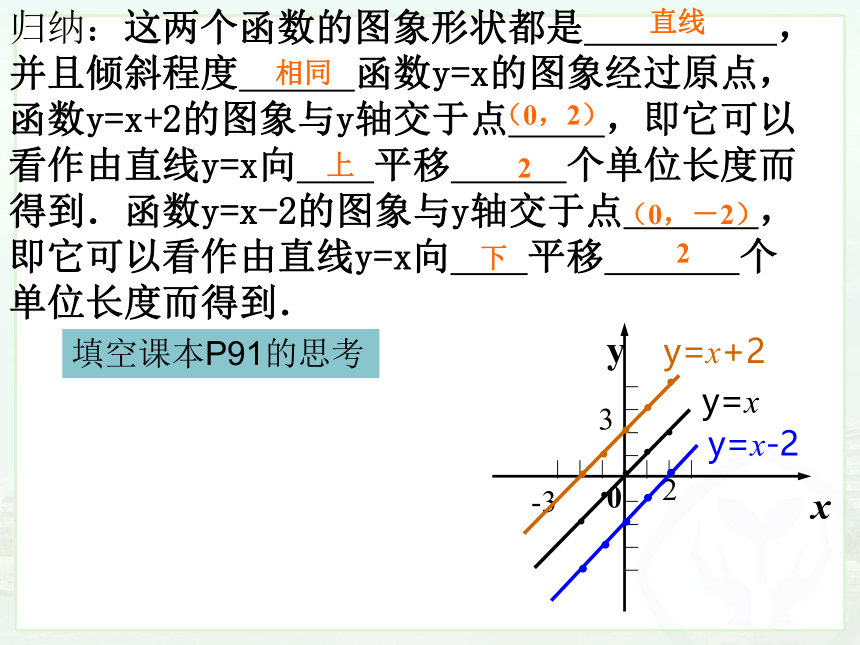
归纳:这两个函数的图象形状都是 ,并且倾斜程度 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移 个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移 个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
填空课本P91的思考
(2)你能说出一次函数y=3x-4的图象是什么形状吗?它与直线y=3x有什么关系?
(3)那么一次函数y=kx+b的图象与正比例函数y=kx图象有什么关系?
一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到。
(当b>0时,向上平移;当b<0时,向下平移)
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
2、用两点法画一次函数图像
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
总结:
画一次函数的图像时,只要描出合适关系式的两点,再连接两点即可,我们通常选
取(0,b)和(- ,0 )这两个点,也就
是选取图像与x轴和y轴的交点坐标。
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
2、用两点法画一次函数图像
你会画出函数y=2x-1与y=-2x+l的图象吗?
y
x
o
2
1
·
·
·
·
y=2x-1
y=-2x+l
结论:1、当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
y
x
o
2
1
·
·
·
·
y=2x-1
y=-2x+l
y=x+1
y=-x-1
议一议:
一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
注意:图象与y轴交于(0,b),b的正负决定图像交于y轴的正或负半轴。
一次函数的图像和性质
练一练
练习1 在同一直角坐标系中画出下列函数的图象,
每小题中三个函数图象有什么关系?
(1)y =x-1,y =x,y =x+1;
(2)y =-2x-1,y =-2x,y =-2x+1.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
练一练
(0,-3)
一、三、四
增大
练习2 直线y =2x-3 与x 轴交点的坐标为________;
与y 轴交点的坐标为________;图象经过____________
象限, y 随x 的增大而________.
(1.5,0)
练习3.已知一次函数y=2x﹣3的大致图象为( )
练一练
练习4 一次函数 y =kx+b,y 随 x 的增大而减小,b
>0,则它的图象经过第____________象限.
一、二、四
1、直线y=3x-2可由直线y=3x向 平移 单位得到。
2、直线y=x+2可由直线y=x-1向 平移 单位得到。
练习5
下
2
上
3
(1)一次函数 y =kx+b(k≠0)的图象是什么形状?
怎样用简便方法画出一个一次函数的图象?
(2)一次函数有哪些性质?一次函数与正比例函数
有什么关系?
(3)我们是怎样对一次函数的性质进行研究的?
课堂小结
y=kx+b(k≠0)
y=kx(k≠0)
图象
平移
k>0时,直线从左向右上升,y 随x 的增大而增大; k<0时,直线从左向右下降,y 随x 的增大而减小.
两点法画一
次函数图象
研究方法:
画图象→观察图象→变量(坐标)意义解释.
课堂小结
一次函数的图像和性质
19.2.2 一次函数(2)
学习目标:
1.会画一次函数的图象;
2.能从图象角度理解正比例函数与一次函数的关
系;
3.能根据一次函数的图象和表达式y =kx+b(k≠0)
理解k>0和k<0时,图象的变化情况. 从而理
解一次函数的增减性;
(1)什么叫正比例函数?从解析式看,正比例函
数与一次函数有什么关系?
(2)正比例函数有哪些性质?是怎样得到这些性
质的?
想一想
正比例函数的图像和性质
既然正比例函数是特殊的一次函数,正比例函数的图象是直线,那么一次函数的图象也会是一条直线。 它们图象之间有什么关系?一次函数的又有什么性质呢?
研究函数 y =kx+b(k≠0)的性质;
研究方法:
画图象→观察图象→变量(坐标)意义解释.
1、请大家在同一坐标系内作出下列函数y=x, y=x+2,y=x-2的图象。
x
…
-2
-1
0
1
2
…
y=x
…
…
y=x+2
…
…
y=x-2
…
…
-2
0
-4
-1
1
-3
0
2
-2
1
3
-1
2
4
0
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
议一议:正比例函数y=x与一次函数y=x+2 、y=x-2图象有什么异同点.
2、观察与比较
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
归纳:这两个函数的图象形状都是 ,并且倾斜程度 函数y=x的图象经过原点,函数y=x+2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移 个单位长度而得到.函数y=x-2的图象与y轴交于点 ,即它可以看作由直线y=x向 平移 个单位长度而得到.
直线
相同
(0,2)
上
2
(0,-2)
下
2
填空课本P91的思考
(2)你能说出一次函数y=3x-4的图象是什么形状吗?它与直线y=3x有什么关系?
(3)那么一次函数y=kx+b的图象与正比例函数y=kx图象有什么关系?
一次函数y=kx+b的图象是一条直线,我们称它为直线y=kx+b,它可以看作由直线y=kx平移|b|个单位长度得到。
(当b>0时,向上平移;当b<0时,向下平移)
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
2、用两点法画一次函数图像
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
总结:
画一次函数的图像时,只要描出合适关系式的两点,再连接两点即可,我们通常选
取(0,b)和(- ,0 )这两个点,也就
是选取图像与x轴和y轴的交点坐标。
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
实践:用两点法在同一坐标系中画出函数y=2x-1
与y=-0.5x+1的图象.
x
y=2x-1
x
y= -0.5x+1
0
0
-1
0
0.5
0
1
2
经过(0,-1)和(0.5,0)两点
经过(0,1)和(2,0)两点
y=2x-1
y=-0.5x+1
2、用两点法画一次函数图像
你会画出函数y=2x-1与y=-2x+l的图象吗?
y
x
o
2
1
·
·
·
·
y=2x-1
y=-2x+l
结论:1、当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小
x
y
3
2
-3
0
.
.
.
.
.
y=x
.
.
.
.
.
.
.
.
.
.
y=x+2
y=x-2
y
x
o
2
1
·
·
·
·
y=2x-1
y=-2x+l
y=x+1
y=-x-1
议一议:
一次函数解析式y=kx+b(k, b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
注意:图象与y轴交于(0,b),b的正负决定图像交于y轴的正或负半轴。
一次函数的图像和性质
练一练
练习1 在同一直角坐标系中画出下列函数的图象,
每小题中三个函数图象有什么关系?
(1)y =x-1,y =x,y =x+1;
(2)y =-2x-1,y =-2x,y =-2x+1.
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
y
x
o
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
练一练
(0,-3)
一、三、四
增大
练习2 直线y =2x-3 与x 轴交点的坐标为________;
与y 轴交点的坐标为________;图象经过____________
象限, y 随x 的增大而________.
(1.5,0)
练习3.已知一次函数y=2x﹣3的大致图象为( )
练一练
练习4 一次函数 y =kx+b,y 随 x 的增大而减小,b
>0,则它的图象经过第____________象限.
一、二、四
1、直线y=3x-2可由直线y=3x向 平移 单位得到。
2、直线y=x+2可由直线y=x-1向 平移 单位得到。
练习5
下
2
上
3
(1)一次函数 y =kx+b(k≠0)的图象是什么形状?
怎样用简便方法画出一个一次函数的图象?
(2)一次函数有哪些性质?一次函数与正比例函数
有什么关系?
(3)我们是怎样对一次函数的性质进行研究的?
课堂小结
y=kx+b(k≠0)
y=kx(k≠0)
图象
平移
k>0时,直线从左向右上升,y 随x 的增大而增大; k<0时,直线从左向右下降,y 随x 的增大而减小.
两点法画一
次函数图象
研究方法:
画图象→观察图象→变量(坐标)意义解释.
课堂小结
一次函数的图像和性质
