人教版八年级下册19.3课题学习 选择方案(1)课件(16张PPT)
文档属性
| 名称 | 人教版八年级下册19.3课题学习 选择方案(1)课件(16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 536.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-05 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
八年级 下册
19.3 课题学习 选择方案(1)
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方
法.
学习重点:
建立函数模型解决方案选择问题.
课件说明
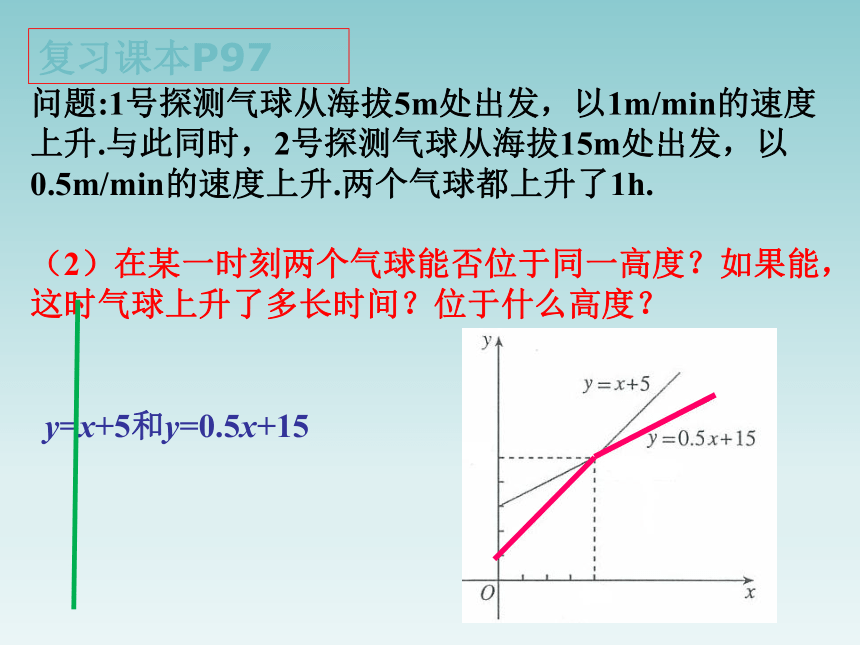
问题:1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.
(2)在某一时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
复习课本P97
y=x+5和y=0.5x+15
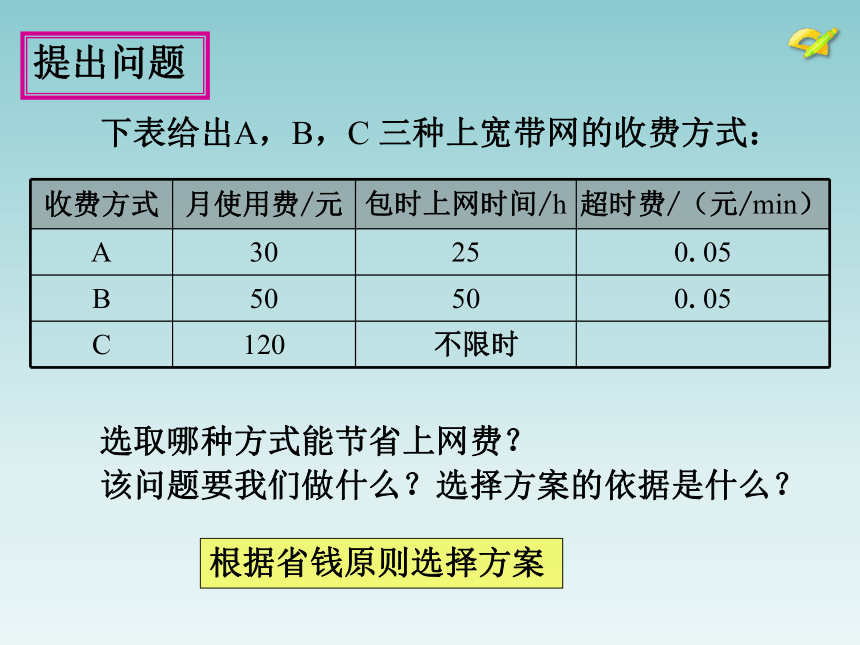
下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
根据省钱原则选择方案
提出问题
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
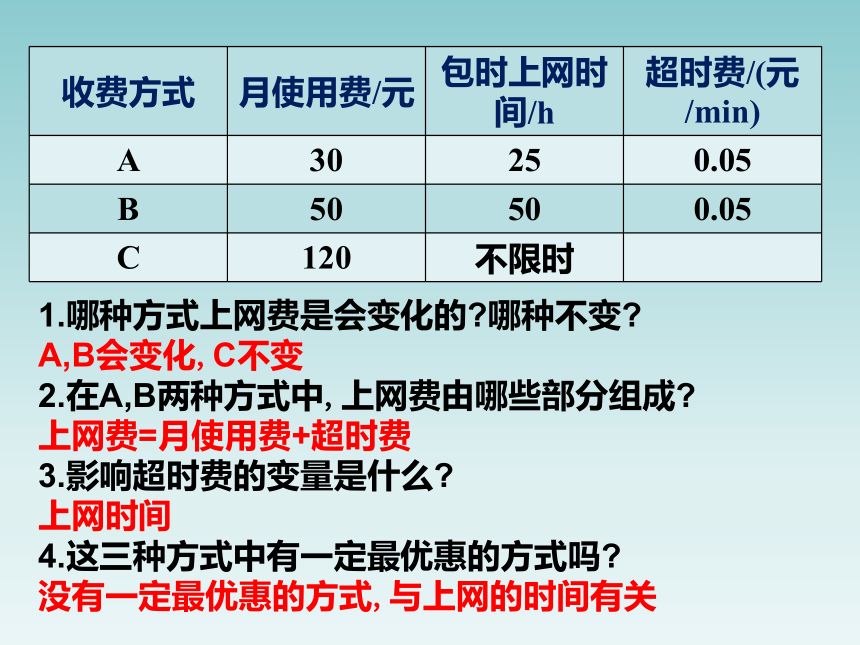
1.哪种方式上网费是会变化的 哪种不变
A,B会变化,C不变
2.在A,B两种方式中,上网费由哪些部分组成
上网费=月使用费+超时费
3.影响超时费的变量是什么
上网时间
4.这三种方式中有一定最优惠的方式吗
没有一定最优惠的方式,与上网的时间有关
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
设月上网时间为x,则方式A,B的上网费y1,y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
在方式A中,超时费一定会产生吗 什么情况下才会有超时费
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
当x≥0时,y3=120.
能把这个问题描述为函数问题吗?
设上网时间为 t,方案A,B,C的上网费用分别为
y1 元,y2 元, y3 元,且
分析问题
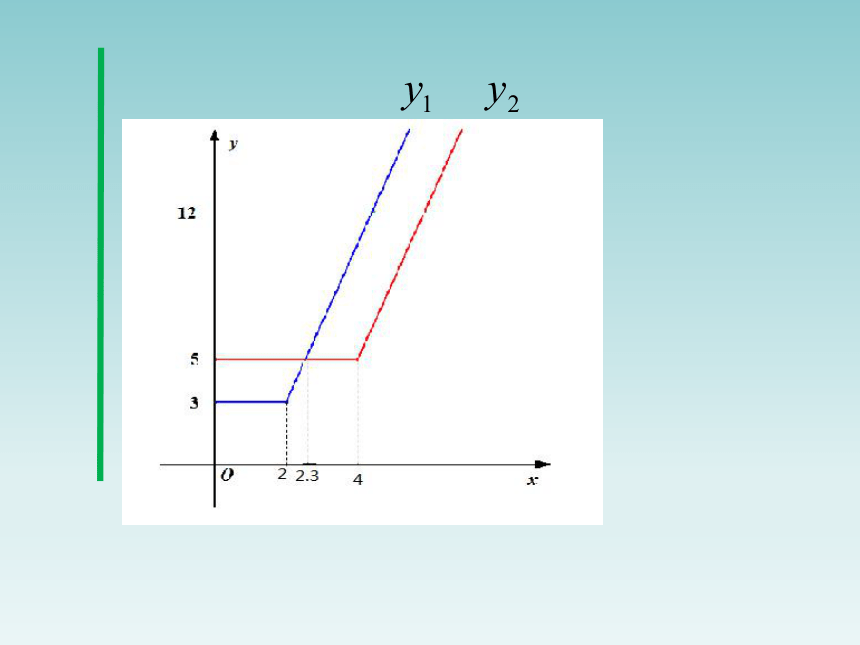
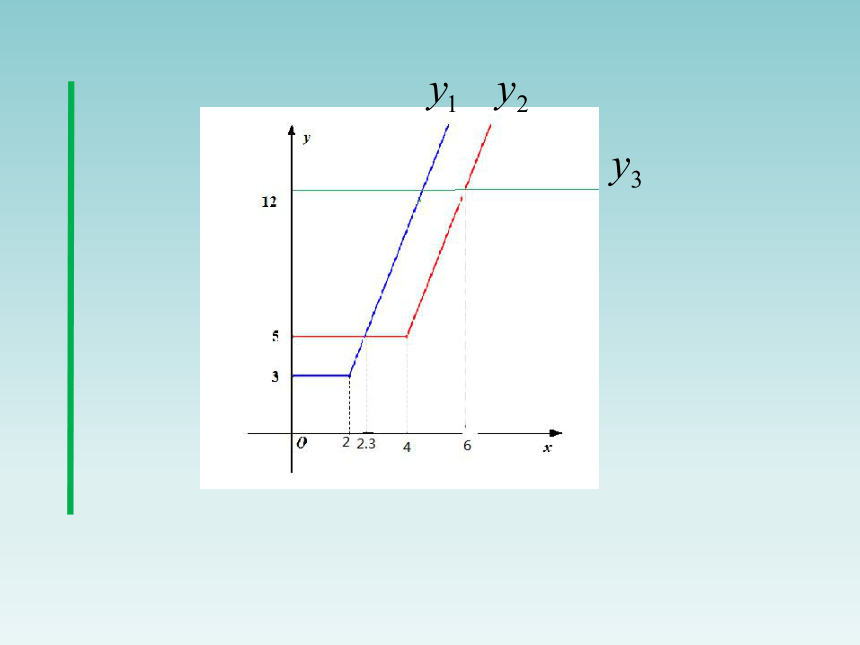
请比较y1,y2,y3的大小.
这个问题看起来还是有点复杂,难点在于每一个函
数的解析都是分类表示的,需要分类讨论,而怎样分类
是难点.怎么办?
——先画出图象看看.
y1=
30, 0≤t≤25;
3t-45, t>25.
y2=
50, 0≤t≤50;
3t-100,t>50.
y3=120.
当上网时间__________时,
选择方式A最省钱.
当上网时间__________
时,选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
实际问题
一次函数问题
设变量
找对应关系
一次函数问题的解
实际问题的解
解释实
际意义
解后反思
这个实际问题的解决过程中是怎样思考的?
分析问题
分类:y1<y2<y3时,y1最小;
y1=y2<y3时,y1(或y2)最小;
y2<y1<y3时,y2最小;
y1>y3,且y2>y3时,y3最小.
y1=
30, 0≤t≤25;
3t-45, t>25.
A
50, 0≤t≤50;
3t-100,t>50.
y2=
B
y3=120.
C
120
50
30
25
50
75
O
t
y
y1
y2
y3
练习
1、如图所示,L1反映了某公司产品的销售收入和销售数量的关系, L2反映产品的销售成本与销售数量的关系,根据图象判断公司盈利时销售量( )
A、小于4件
B、大于4件
C、等于4件
D、大于或等于4件
B
如图是甲、乙两家商店销售同一种产品的销售价y元与销售量x件之间的函数图象,下列说法(1)售2件时,甲、乙两家的售价相同;(2)买一件时买乙家的合算;(3)买3件时买甲家的合算;(4)买乙家的1件售价约为3元。其中说法正确的是: .
(1) (2) (3)
八年级 下册
19.3 课题学习 选择方案(1)
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方
法.
学习重点:
建立函数模型解决方案选择问题.
课件说明
问题:1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都上升了1h.
(2)在某一时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?
复习课本P97
y=x+5和y=0.5x+15
下表给出A,B,C 三种上宽带网的收费方式:
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
根据省钱原则选择方案
提出问题
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
1.哪种方式上网费是会变化的 哪种不变
A,B会变化,C不变
2.在A,B两种方式中,上网费由哪些部分组成
上网费=月使用费+超时费
3.影响超时费的变量是什么
上网时间
4.这三种方式中有一定最优惠的方式吗
没有一定最优惠的方式,与上网的时间有关
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
设月上网时间为x,则方式A,B的上网费y1,y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时
(1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
在方式A中,超时费一定会产生吗 什么情况下才会有超时费
超时费不是一定有的,只有在上网时间超过25h时才会产生.
上网费=月使用费+超时费
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
问题一:怎样选取上网收费方式——分析问题
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
当x≥0时,y3=120.
能把这个问题描述为函数问题吗?
设上网时间为 t,方案A,B,C的上网费用分别为
y1 元,y2 元, y3 元,且
分析问题
请比较y1,y2,y3的大小.
这个问题看起来还是有点复杂,难点在于每一个函
数的解析都是分类表示的,需要分类讨论,而怎样分类
是难点.怎么办?
——先画出图象看看.
y1=
30, 0≤t≤25;
3t-45, t>25.
y2=
50, 0≤t≤50;
3t-100,t>50.
y3=120.
当上网时间__________时,
选择方式A最省钱.
当上网时间__________
时,选择方式B最省钱.
当上网时间_________时,
选择方式C最省钱.
实际问题
一次函数问题
设变量
找对应关系
一次函数问题的解
实际问题的解
解释实
际意义
解后反思
这个实际问题的解决过程中是怎样思考的?
分析问题
分类:y1<y2<y3时,y1最小;
y1=y2<y3时,y1(或y2)最小;
y2<y1<y3时,y2最小;
y1>y3,且y2>y3时,y3最小.
y1=
30, 0≤t≤25;
3t-45, t>25.
A
50, 0≤t≤50;
3t-100,t>50.
y2=
B
y3=120.
C
120
50
30
25
50
75
O
t
y
y1
y2
y3
练习
1、如图所示,L1反映了某公司产品的销售收入和销售数量的关系, L2反映产品的销售成本与销售数量的关系,根据图象判断公司盈利时销售量( )
A、小于4件
B、大于4件
C、等于4件
D、大于或等于4件
B
如图是甲、乙两家商店销售同一种产品的销售价y元与销售量x件之间的函数图象,下列说法(1)售2件时,甲、乙两家的售价相同;(2)买一件时买乙家的合算;(3)买3件时买甲家的合算;(4)买乙家的1件售价约为3元。其中说法正确的是: .
(1) (2) (3)
